
Impatience Mechanism in Saddles’ Crossing
Iwona Karcz-Duleba
Institute of Computer Engineering, Control and Robotics, Wroclaw University of Technology,
Wyb. Wyspianskiego 27, 50-370 Wroclaw, Poland
Keywords:
Phenotypic Evolution, Impatience Operator Without and with Knowledge, Polarization of Population,
Bimodal Fitness Function.
Abstract:
Evolutionary inspired heuristics suffer from a premature convergence at local optima and, consequently, a pop-
ulation diversity loss. Thus, breaking out of a local optimum trap and crossing saddles between optima in
multimodal and multidimensional search spaces is an important issue in an evolutionary optimization algo-
rithm. In this paper, an impatience mechanism coupled with a phenotypic model of evolution is studied. This
mechanism diversifies a population and facilitates escaping from a local optima trap. An impatient population
polarizes itself and evolves as a dipole centered around an averaged individual. The operator was modified by
supplying it with an extra knowledge about a currently found optimum. In the case, behavior of a population
is quite different – a significant diversification is observed but the population is not polarized and evolves as
a single cluster. Both mechanisms allow to cross saddle relatively fast for a wide range of parameters of a
bimodal multidimensional fitness function.
1 INTRODUCTION
An indisputable success of evolutionary inspired
heuristics in optimization results from efficiency in
dealing with complex optimization problems. How-
ever,the methods are not free from drawbacks. One of
the most important among them is a search stoppage
at local optima which usually results in loss of a popu-
lation diversity and limited ability to leave the optima
and finding other, possibly better, ones. Many strate-
gies of regaining a population diversity and maintain-
ing multiple solutions for multimodal fitness func-
tions were proposed. Techniques of crowding (De-
Jong, 1975; Mengshoel and Goldberg, 2008), fitness
sharing (Goldberg and Richardson, 1987; Sareni and
Kr¨ahenb¨uhl, 1998) and spatially-structured popula-
tions (Tomassini, 2005; Dick and Whigham, 2006)
were designed just for the task.
In many practical applications, it is more impor-
tant to quickly find a better than a current best solution
rather than to maintain multiple solutions in a long-
lasting process. We can call this task a “local global
optimization”. While solving the task, crossing sad-
dles between optima by a population actually being in
a state of quasi-equilibrium around a local optimum
becomes a key problem. Softing a selective pressure
and taking a small population size may help in leaving
a current optimum. Selections with a soft selective
pressure allow for survival also worse adapted indi-
viduals thus a mean population fitness decreases and
a chance of a saddle crossing increases (Galar, 1989;
Goldberg and Deb, 1991; Chorazyczewski and Galar,
1998), (Chen et al., 2010). Smaller populations are
more mobile than bigger ones and they are also sus-
ceptible to a genetic drift what makes saddles cross-
ing easier (Rogers and Pr¨ugel-Bennett, 1999; Karcz-
Duleba, 2006). Other ideas proposed to facilitate sad-
dle crossing are based on modification either a fit-
ness function (Obuchowicz, 1997) or individual fit-
ness values. Methods based on fitness sharing (Gold-
berg and Richardson, 1987) or exploiting a mecha-
nism of impatience (Galar and Kopciuch, 1999) can
be classified to the latter group. The method of fitness
sharing is based on the concept of finite resources to
encourage elements of the population to explore dif-
ferent regions of the fitness function. The impatience
mechanism modifies fitness of impatient individuals
within a population trapped at a local optimum and
promotes those individuals located on periphery of
a population cloud. The mechanism causes polariza-
tion of a population which evolves as a dipole cen-
tered at a population mean. In this paper a modifica-
tion of the impatience operator is proposed. It relies
on adding extra knowledge concerning location of a
local optimum.
Those versions of the impatience mechanism will
176
Karcz-Duleba I..
Impatience Mechanism in Saddles’ Crossing.
DOI: 10.5220/0005054201760183
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 176-183
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

be studied in details in this paper which is organized
as follows. In Section 2 a model of phenotypic evo-
lution with an operator of impatience and population
polarization mechanisms are described. The operator
of impatience with an extra knowledge about a local
optimum is depicted in Section 3. In Section 4 re-
sults of simulation studies are presented. Section 5
concludes the paper.
2 OPERATOR OF IMPATIENCE
2.1 Model of Evolution with Impatience
An operator of impatience was first introduced into
a model of a simple phenotypic asexual evolution
(Galar, 1989) in the paper (Galar and Kopciuch,
1999). A population composed of m elements is de-
scribed in an n-dimensional unbounded real search
space R
n
. The evolution is subordinated to a pro-
portional selection and a Gaussian mutation with the
standard deviation σ. The model is generational
what means that the whole population is replaced
in every generation. An operator of impatience re-
places an original fitness of an individual by a fit-
ness depending on the distance from a mean individ-
ual within a population.
More formally, let x
j
∈ R
n
is a position of the jth
individual characterized by its fitness q
j
(x) and d
j
de-
notes a distance of this individual from the popula-
tion mean. A modified fitness of the j-th individual is
given by
q
a
(x
j
) = (
d
j
d
A
+ c)q(x
j
) (1)
where d
A
is an average distance of all individuals from
the mean of the whole population
x =
1
m
m
∑
i=1
x
i
, d
A
=
1
m
m
∑
i=1
kx
i
−
xk =
1
m
m
∑
i=1
d
i
and c is a constant parameter taken from interval
[0,1]. Some past (Galar and Kopciuch, 1999) and
preliminary results have revealed a negligible influ-
ence of parameter c on performance of the impatience
mechanism, therefore its value will be set to c = 1
later on.
An impact of the operator of impatience on cross-
ing saddles was studied in an adaptive landscape
of the n-dimensional bimodal fitness function being
a sum of two bell shaped functions with different
heights forming a distinct saddle
q(x) = exp(−a
1
n
∑
k=1
x
2
k
)+hexp(−a
2
(x−1)
2
+a
2
n
∑
k=2
x
2
k
)
(2)
a)
−1 −0.5 0 0.5 1
0
1
2
3
4
5
6
7
q(x)
d
A
=0.05
d
A
=0.1
d
A
=0.5
b)
−1
0
1
−1
−0.5
0
0.5
1
0
1
2
3
4
Figure 1: a) A fitness transformation of one-dimensional
local optimum hill q (denoted by a dotted line) by the op-
erator of impatience (1) for three population mean loca-
tions: d
A
= 0.05,0.1,0.5. b) a fitness transformation of
two-dimensional local optimum hill q by operator of im-
patience (1), d
A
= 0.1.
where h ≥ 1. A local optimum with a height equal
to one is located at x
l
= (0,0,..., 0) and the global
optimum with the height h = 2, shifted in the first co-
ordinate, is located at x
g
= (1,0,...,0). Parameters
a
1
, a
2
influence slopes of both hills. In all experi-
ments presented, a slope of the local hill was set to
a
1
= 5 (by rescaling coordinates linearly any other
case of quality function (2) can be transformed into
the case considered). The global hill becomes slim-
mer and slimmer as parameter a
2
increases and, con-
sequently, a saddle between both optima is wider and
deeper (see also Fig. 14.a). The width ∆
s
of a saddle
was defined as the shortest distance between the top
of the local hill and a point at the global hill with the
same value as at the local optimum attains. Later on
the parameter was scaled in units of standard devia-
tion of mutation σ and depicted as ∆
′
s
.
The operator of impatience decreases quality of
individuals close to the population mean and in-
creases quality of those located at peripheries of the
population, i.e. distant from the population mean.
In Fig. 1 exemplary transformations, according to
Eq. (1), of one- and two-dimensional fitness func-
tion (2) is presented. As the operator of impatience is
ImpatienceMechanisminSaddles'Crossing
177

a) after generation No. 30
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
b) after generation No. 40
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
c) after generation No. 60
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
Figure 2: Stages of saddle crossing by a polarized popula-
tion, m = 32, n = 2, σ = 0.025.
applied to the population placed around the local hill,
only the first (local) component of Eq. (2) was visu-
alized. Fitness values of individuals located far away
from the population mean increases significantly and,
what is more interesting, the function is not symmet-
rical.
2.2 Polarization of Population
The action of the operator of impatience is illustrated
in Fig. 2. As mentioned before, the operator increases
the effective adaptation of those individuals located
on the boundary of a population cluster by increas-
ing probability of their selection (cf. Fig. 1). Thus,
the distant from the mean individuals reproduce more
intensively and increase a population diversity. Too
large dispersion of a population is counteracted by
a decrease in fitness of far-away-from-optimum indi-
viduals subjected to selection. Consequently, a pop-
ulation is located on some kind of orbit around the
population mean where both trends are in balance and
the orbit acts as an attractor for a fluctuating, around
an optimum, population. Additionally, some loca-
tions on the orbit are favored (two optima in Fig. 1.a).
In effect, a population polarizes and spontaneously
breaks into two clustered sub-populations spawning a
kind of dipole (Fig. 2.a). The dipole fluctuates along
the orbit. A number of individuals that belong to each
sub-population changes dynamically.
When a local hill is separated from another opti-
mum by a saddle, a dipole may be attracted by the
saddle where the adaptation is slightly higher than on
other parts of the orbit, and directed its axis along the
saddle (Fig. 2.b). In result, a saddle can be crossed
faster by this part of a dipole situated closer to a
saddle. A saddle crossing is done by one of the
sub-populations whereas the other one remains some-
where around a local hill. Remaining one of sub-
populations on a local optimum may be explained
when looking at Fig. 1.a and a function depicted to
a mean of population d
A
= 0.5. In the case, sub-
population is about to cross a saddle which is ∆
s
= 0.6
wide. Transformed fitness of individuals on a local
hill is very high comparing to individuals just cross-
ing saddles, so they stay on a local optimum (Fig. 2.c).
This sub-population slowly becomes extinct after sad-
dle crossing as individuals on the global hill repro-
duce themselves more often.
The comparison of a phenotypic evolution with
proportional selection and Gaussian mutation with
and without impatience mechanism involved is pre-
sented in Fig. 3. Evolution of both populations was
initialized at a local hill, starting with a uniform pop-
ulation of sub-optimal individuals. For a population
treated by the operator of impatience, the operator
was turned on after five generations, letting for a pre-
liminary diversification of clones. Such a popula-
tion imitates a state of quasi-stability around the local
optimum. The polarized population is much widely
distributed and crossed a saddle before a population
without impatience.
In Figs. 4-5 some statistics of both populations
from Fig. 3 are presented. The diversification of
a population was defined as an average distance from
the mean individual. For a population with the impa-
tience operator, the diversification is higher than for
the population without it, i.e. distances from a popula-
tion mean for polarized population are larger than for
non-polarized one (Fig. 4). Thus, the impatience op-
erator may be classified into diversification preserving
methods. An averagefitness of the population without
the impatience mechanism is changed slightly (about
10%) and remains at a similar level whereas the fit-
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
178

a)
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
b)
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
Figure 3: Evolution without (a) and with (b) operator of
impatience; traces of all generations from No. 1 to No. 80
are presented; m = 32, n = 2, σ = 0.025.
0 20 40 60 80
0
0.1
0.2
0.3
0.4
without impatience
with impatience
Figure 4: Diversification of populations - an average dis-
tance from the mean individual for populations from Fig. 3.
ness of the population with the impatience operator is
greatly reduced (about 20%-30%), what may help in
saddle crossing (Fig. 5).
3 IMPATIENCE WITH
KNOWLEDGE
The operator of impatience is switched on when
a population gets stuck at a quasi-equilibrium state
around a currently found optimum. Thus, the value
of the optimum either is known or can be reliably es-
timated. So, we decided to include the extra knowl-
edge about the optimum placement into the operator
of impatience and studied its influence on population
dynamics.
0 20 40 60 80
0.7
0.8
0.9
1
1.1
without impatience
with impatience
Figure 5: Average fitness of populations from Fig. 3.
Consequently, operator (1) is changed in such
a way that the distance from the population mean is
replaced with the distance from the (estimated) op-
timum. A modified fitness of the j-th individual lo-
cated at distance d
jo
from the local optimum is now
described by equation
q
K
(x
j
) = (
d
jo
d
Ao
+ c)q(x
j
) (3)
where d
Ao
denotes an average distance from the opti-
mum for the whole population
d
Ao
=
1
m
m
∑
i=1
kx
i
− x
∗
k =
1
m
m
∑
i=1
d
io
and x
∗
is a placement of the local (possibly estimated)
optimum.
While studying populations in a landscape of fit-
ness function (2) with the local optimum placed at
x = 0, it is possible to figure out (cf. Fig. 6) how
an individual fitness, described by Eq. (3), is modi-
fied. Similarly to Fig. 6 only the first (local) com-
ponent of Eq. (2) and, as the transformation Eq. (3)
is symmetrical, only positive half-plane was visual-
ized. The upper panel presents the modified one-
dimensional local optimum for two values of average
distance d
Ao
= 0.1, 0.2. The bottom panel displays
a two-dimensional local optimum hill transformation
for d
Ao
= 0.1. The operator of impatience with knowl-
edge decreases a quality of near optimal individuals
and increases of those located at some distance from
the optimum. When a population is closer to a lo-
cal optimum (i.e. the average distance d
Ao
is getting
small), a transformed quality of some distant individ-
uals highly inceases (more than twice). When the
population is more dispersed, d
Ao
is relatively large,
the transformed quality of an individual is smaller but
still exceeds the local hill quality.
In Fig. 7 stages of saddle crossing by the popu-
lation influenced by the operator of impatience with
knowledge are presented. The main difference be-
tween the operator of impatience with and with-
out knowledge is clearly visible: the population, for
ImpatienceMechanisminSaddles'Crossing
179

a)
0 0.2 0.4 0.6 0.8 1
0
0.5
1
1.5
2
2.5
3
q(x)
d
Ao
=0.1
d
Ao
=0.2
b)
−1
−0.5
0
0.5
1
−1
−0.5
0
0.5
1
0
1
2
3
Figure 6: a) A fitness transformation of one-dimensional
local optimum hill q (denoted by a dotted line) by the op-
erator of impatience with knowledge (3) for two average
distances: d
Ao
= 0.1,0.2. b) the fitness transformation of
two-dimensional local optimum hill q by operator of impa-
tience, d
Ao
= 0.1.
which operator of impatience is calculated acording
to Eq. (3) is widely diversified but it is not polarized
(cf. Fig. 2). The difference can be explained as fol-
lows. Populations evolved without knowledge have
got no information about a fitness function configu-
ration. Their knowledge is restricted to information
about an actual population itself. When operator with
knowledge (3) is acting, population is located on an
orbit around the local optimum. All locations on the
orbit are equally likely (cf. Fig. 6). Additionally, ex-
isting in evolving populations tendency to concentrat-
ing individuals imply that population is not polarized
and evolves as a cluster, but is more dispersed than
population without impatience operator.
Informative characteristics (diversification, aver-
age fitness, averagedistances from the local optimum)
of populations evolved with the operator of impa-
tience with and without knowledge are depicted in
Figs. 8-10. Both simulations were stopped after 60
generations, just after crossing a saddle by some in-
dividuals but not by the population mean (what can
be seen in the average fitness plot c.f. Fig. 8). In all
figures, the operator of impatience with knowledge
was marked as wK (with Knowledge). The average
fitness of both populations are similar: after turning
a) generation No. 30
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
b) generation No. 60
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
c) generation No. 120
−0.5 0 0.5 1 1.5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
Figure 7: Stages of saddle crossing by a population sub-
jected to the operator of impatience with knowledge, m =
32, n = 2, σ = 0.025.
0 10 20 30 40 50 60
0.7
0.8
0.9
1
1.1
with impatience
with impatience wK
Figure 8: An average fitness of populations evolved with the
operator of impatience with (wK) and without knowledge
after 60 generations, m = 32, n = 2, σ = 0.025.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
180

0 10 20 30 40 50 60
0
0.1
0.2
0.3
0.4
0.5
with impatience
with impatience wK
Figure 9: Diversification of population - an average distance
of population individuals from the mean for whole popula-
tions evolving with the operator of impatience with (wK)
and without extra knowledge after 60 generations, m = 32,
n = 2, σ = 0.025.
a)
0 10 20 30 40 50 60
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
average for individuals
for mean of population
b)
0 10 20 30 40 50 60
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
average for individuals
for mean of population
Figure 10: An average distance of population individuals
from the local optimum and the distance of the population
mean from the local optimum. Evolution with the operator
of impatience: a) without knowledge, b) with knowledge
(wK) after 60 generations, m = 32, n = 2, σ = 0.025.
on the operator fitness decreases about 20-30% and
while crossing saddle fitness increases again (Fig. 8).
In order to understand actions of both operators bet-
ter, not only distances of individuals from the popula-
tion mean but also distances from the local optimum
were calculated. Populations evolved with the opera-
tor of impatience without knowledge is polarized, so
it is more dispersed than the population with knowl-
edge. The average distance of population individuals
from the population mean for the operator of impa-
tience without knowledge is growing during the pre-
sented evolution run and achieved quite a high value
after crossing sadle as polarized sub-populations are
located on both optima (Fig. 9). For the impatience
operator with knowledge, the average distance re-
mains on similar level during evolution on a local hill
and increases only slightly while crossing a saddle.
Distances from the local optimum for both operators
were calculated for the mean individual and averaged
for all population individuals (Fig. 10). The mean in-
dividual of population evolved with the operator of
impatience without knowledge is located close to the
optimum until population crossed saddle. This means
that while population wanders around the local opti-
mum, a center of the dipol is located very close to
optimum. When population crossed a saddle, the dis-
tance to the local optimum inreases and the center of
the dipol moves towards the global optimum. An av-
erage distance of individuals from the local optimum
increases slowly as a population is diffused and one
sub-population crossed a saddle. For the operator of
impatience with knowledge both distances are very
similar as a population is not polarized and evolves as
whole.
4 EFFICIENCY OF CROSSING
SADDLES: SIMULATION
RESULTS
The efficiency of crossing a saddle by a popula-
tion subjected to the operator of impatience with
and without knowledge was studied for fitness func-
tion (2). The total number of fitness function evalua-
tion needed to cross a saddle and averaged over 1000
runs was selected as a performance criterion. Compu-
tations were terminated when a hypotetical, average
individual crossed a saddle, i.e. the average popula-
tion fitness exceeded the value of the local optimum.
Results were related to the phenotypic evolution with
a proportional selection and the Gaussian mutation
without using the impatience operator.
An influence of the following parameters on cross-
ing saddles were tested:
• population size m (Fig. 11),
• search space dimension n (Fig. 12),
• saddle width ∆
′
s
(scaled in units of standard devi-
ation of mutation σ) (Fig. 13),
• saddle depth (depending on a slope, a
2
, of the
global optimum) (Fig. 14).
If not varied, the values of other parameters m = 16,
n = 4, σ = 0.05, a
2
= 5, ∆
′
s
= 12 were set. Because
the slope a
2
of the global optimum causes not only
ImpatienceMechanisminSaddles'Crossing
181

48 16 32 64 128
10
2
10
3
10
4
10
5
without impatience
with impatience
with impatience wK
Figure 11: Efficiency of saddle crossing - impact of popu-
lation size m.
2 4 8 16
10
2
10
3
10
4
10
5
without impatience
with impatience
with impatience wK
Figure 12: Efficiency of saddle crossing - impact of a search
space dimension n.
5 10 20 40
10
2
10
3
10
4
10
5
without impatience
with impatience
with impatience wK
Figure 13: Efficiency of saddle crossing - impact of saddle
width ∆
′
s
(scaled in units of standard deviation of mutation).
deepening but also widening of a saddle, for every a
2
an appropriate value of σ was calculated (Fig. 14.a,
Tab. 1) to preserve a constant saddle width ∆
′
s
= 12.
As it can be seen in Figs. 11-14, an evolution
exploiting the impatience operator outperforms its
impatience-free version in a wide range of parameters
of the fitness function and the model. An extra knowl-
edge concerning the location of the local optimum
accelerates crossing saddles only slightly. The big-
ger benefit is obtained for large populations (m = 32–
128). What is more interesting, increasing a popula-
tion size does not increase significantly the number
of fitness function calculations needed to cross a sad-
dle (Fig. 11). Efficiency of the three evolution models
Table 1: Values of σ for different parameters a
2
to preserve
a constant saddle width ∆
′
s
= 12 (scaled in units of σ).
a
2
5 10 20
σ 0.05 0.063 0.071
a)
−1 −0.5 0 0.5 1 1.5 2
0
0.5
1
1.5
2
a
2
=5
a
2
=10
a
2
=20
∆
s
b)
5 10 20
10
2
10
3
10
4
10
5
without impatience
with impatience
with impatience wK
Figure 14: a) Profile of fitness function (2) for different pa-
rameters a
2
with depicted unscaled value of ∆
s
. b) Effi-
ciency of saddle crossing - impact of a saddle depth (de-
pending on the slope parameter a
2
).
Table 2: Number of generations needed to find 2nd and 3rd
optimum averaged over 100 runs and the number of unsuc-
cessful runs; m = 32, σ = 0.2.
knowledge 2nd opt. 3rd opt. unsuccess.
without 362 403 6
with 417 454 7
were similar for small search space dimensionallities
n = 2–8 (Fig. 12), although the model without im-
patience is slightly worse. As the dimensionallity n
grows, the efficiency of model with impatience and
knowledge decreases and resembes that without im-
patience. The best performance displayed the model
with impatience. Populations evolving with the im-
patience operator crossed efectivelly large and deep
saddles (Figs. 13-14) and the efficiency of both ver-
sions of the operator are comparable.
Aforementioned examples are rather simple but
recent results concerning more difficult quality func-
tions are promissing. In Fig. 15 the optimisation of
multimodal Ursem 03 test function
f
U
(x,y) = sin(2.2πx+ 0.5π)(2 − |y|)(3− |x|)/4+
+ sin(0.5πy
2
+ 0.5π)(2− |y|)(2− |x|)/4
using the operator of impatience without knowledge
is illustrated. The initial population was located on
the first optimum and calculations were terminated af-
ter 5000 generations. In Table 2 average results of 100
runs are presented. In this case the impatience opera-
tor without knowledge is a little bit more efficient that
that with the knowledge.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
182
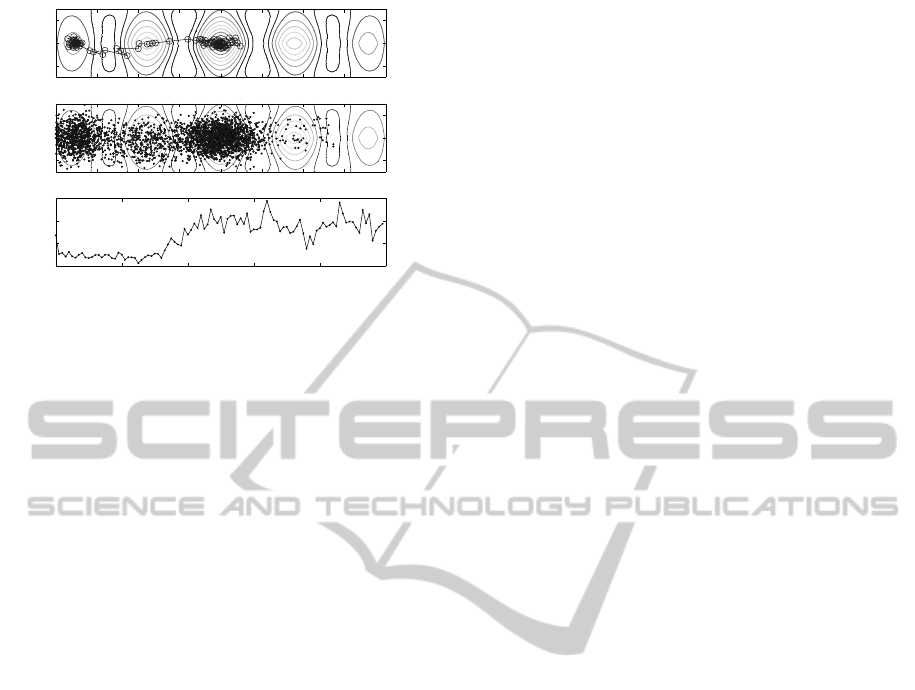
−2 −1.5 −1 −0.5 0 0.5 1 1.5 2
−1
0
1
−2 −1.5 −1 −0.5 0 0.5 1 1.5 2
−1
0
1
0 20 40 60 80 100
0
0.5
1
1.5
Figure 15: Ursem function optimization with the operator
of impatience without knowledge. Upper panel: population
mean location; middle panel: paths of all individuals; lower
panel: average fitness; m = 32, n = 2, σ = 0.2.
5 CONCLUSIONS
In this paper a mechanism of impatience was checked
as a method to preserve diversifiction of a popula-
tion and thereby escaping a local optimum trap. Two
versions of the impatience operator were examined:
with and without extra knowledge concerning (esti-
mated) position of a local optimum. Both versions
increase diversity of population. However, when an
impatience is related to a current population mean, the
polarization of a population was observed (a popula-
tion is divided into dipol-like sub-populations). When
the impatience operator is related to a local optimum
placement the polarization effect was not observed.
In contrary to other diversity preserving methods
(fitness sharing and clearing), the impatience mecha-
nism is parameter-free and increases a computational
effort only slightly. The mechanism is related to a cur-
rent population state and/or already explored parts of
a search space, so it can be used in dynamical land-
scapes.
Actions of both versions of impatience operators
were tested to check the efficiency of crossing a sad-
dle between the local and the global optimum of bi-
modal multidimensional fitness functions. Both ver-
sions demonstrated high efficiency in crossing mul-
tidimensional, width and deep saddles. Preliminary
results of applying the mechanisms to more complex
test functions are promissing and they will stimulate
our future work.
ACKNOWLEDGEMENTS
I want to thank Prof. R. Galar for encouraging me to
rediscover oldies-but-goldies ideas as well as for con-
tinuous and fruitful discussions on the subject.
REFERENCES
Chen, T., He, J., Chen, G., and Yao, X. (2010). Choosing
selection pressure for wide-gap problems. Theoretical
Computer Science, 411(6):926–934.
Chorazyczewski, A. and Galar, R. (1998). Visualization of
evolutionary adaptation in R
n
. In Evolutionary Pro-
gramming VII, pages 657–668.
DeJong, K. (1975). An analysis of the behavior a class of
genetic adaptive systems. PhD thesis, University of
Michigan.
Dick, G. and Whigham, P. A. (2006). Spatially-structured
evolutionary algorithms and sharing: Do they mix? In
et al., T. W., editor, SEAL 2006, LNCSno. 4247, pages
457–464. Springer-Verlag.
Galar, R. (1989). Evolutionary search with soft selection.
Biological Cybernetics, 60:357–364.
Galar, R. and Kopciuch, P. (1999). Impatience and polar-
ization in evolutionary processes. In Proc. of KAEiOG
Conference, pages 115–122. in Polish.
Goldberg, D. and Deb, K. (1991). A comparative analy-
sis of selection schemes used in genetic algorithms.
In Foundations of Genetic Algorithms, pages 69–93.
Morgan Kaufmann.
Goldberg, D. and Richardson, J. (1987). Genetic algorithms
with sharing for multi-modal function optimisation. In
Proc. of the 2nd Int. Conf. on Genetic Algorithms and
Their Applications, pages 41–49.
Karcz-Duleba, I. (2006). Dynamics of two-element popula-
tions in the space of population states. IEEE Transac-
tions on Evolutionary Computation, 10(2):199–209.
Mengshoel, O. and Goldberg, D. (2008). The crowding ap-
proach to niching in genetic algorithms. Evolutionary
Computation, 16(3):315–354.
Obuchowicz, A. (1997). The evolutionary search with soft
selection and deterioration of the objective function.
In Proc. 6th Int. Conf. Intel. Inform. Systems, pages
288–295.
Rogers, A. and Pr¨ugel-Bennett, A. (1999). Genetic drift in
genetic algorithm selection schemes. IEEE Transac-
tions on Evolutionary Computation, 3(4):298–303.
Sareni, B. and Kr¨ahenb¨uhl, L. (1998). Fitness sharing and
niching methods revisited. IEEE Transactions on Evo-
lutionary Computation, 2(3):97–106.
Tomassini, M. (2005). Spatially structured evolutionary al-
gorithms. Springer-Verlag.
ImpatienceMechanisminSaddles'Crossing
183
