Process Characterization and Evaluation of NC Machining Processes

based on Macroscopic Engagement Simulation

Meysam Minoufekr, Pascal Schug and Mihir Joshi

CAx-Technologies, Fraunhofer-Insitute for Production Technology, Steinbachstr. 17, 52074 Aachen, Germany

Keywords: Numerical Control Machining Simulation, NC Machining Process Evaluation, Material Removal

Simulation.

Abstract: With a view to achieve stable production, nowadays the process design and planning goes through a time

and resource intensive correction loop. The process output after machining trials is used to determine the

critical process sections, and hence the experience of the process designer is decisive in the productivity of

the optimization loop and the process. The implementation of a machining simulation can enhance the

productivity of the process design and planning phase. The macroscopic engagement simulation provides an

efficient tool for process evaluation. Moreover, it provides a basis for derivation of microscopic geometric

process parameters, which have a direct correlation to mechanical and thermal loads. Thus, detailed

information relating to the cutting loads on the tool is derivable at every point on the toolpath, enabling

analysis of NC machining process based purely on the macroscopic geometric engagement between the

cutting tool and workpiece. This information regarding the engagement conditions can be used to

proactively identify potential critical process sections in a virtual environment thereby increasing the

process reliability. Thus a process design for an optimal tool load is possible resulting in improved tool life,

process efficiency and reduction in utilised resources.

1 INTRODUCTION

Milling technology is the most commonly used

material removal method in the manufacturing of

high value components, such as the turbine blades,

bladed discs (blisks), press tools (moulds and dies)

etc. These components are characterized by a

complex geometry of sculpted or free formed

surfaces (Choi et al., 1998). Moreover, aerospace

components are manufactured from Titanium and

Nickel based alloys which have high strength and

temperature resistance but poor machinability which

is a challenge in manufacturing. (Klocke, 2011).

Due to the complex geometry of the parts needed in

the mentioned industry sectors, there is a complex

kinematic of the machining processes. This leads to

variable contact conditions and variable load

between workpiece and cutting tool, followed by

acceleration of tool wear.

The state of the art CAx process chain is

depicted in Figure 1, where CAx stands for

computer based technology. The process design is

performed on the basis of information derived

from the simulation tests, and study of fundamental

Figure 1: CAx process chain.(Minoufekr et al., 2013).

process kinematics i.e. orthogonal cutting conditions

(Minoufekr et al., 2013, Zabel, 2010). A process

design based on the fundamental studies leads to

selection of conservative process parameters,

resulting in reduction of productivity. Moreover, the

critical sections in the process are first captured

during the stage of the NC machining the actual part

geometry. Thus, for a stable production with an

optimal process, an optimization loop of the NC

machining is necessary (Schug, 2012). If this

process is carried out in a simulation environment

and verified virtually, improvement in productivity

and reduction in costs can be achieved (Zabel,

2010).

661

Minoufekr M., Schug P. and Joshi M..

Process Characterization and Evaluation of NC Machining Processes based on Macroscopic Engagement Simulation.

DOI: 10.5220/0005054606610670

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 661-670

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

The process analysis in a simulation environment

enables the process designer to understand the

critical section in the process. With this information

pertaining to the process technology, an optimal

process design is possible. Thus this paper presents

an approach to create the technological basis

necessary for the analysis of multi-axis NC milling

processes. Section 2 provides a brief overview of the

existing machining simulation systems, and the

macro-simulation results are described. In Section 3,

directly derivable process characteristics are

assessed based on macro simulation. Furthermore,

the macroscopic simulation results are extended to

derive extra process knowledge regarding the

machining conditions. This is necessary for process

characterization and the subsequent evaluation of

NC machining processes. The paper is concluded in

Section 4.

2 TECHNOLOGICAL

BACKGROUND

AND PROBLEM DEFINITION

With the increase in the importance of the multi-axis

milling processes in the industry, the deployment of

computer based technologies (CAx technologies) is

imperative. The computer based technologies are

involved in the planning and verification of the

entire milling process in advance (refer Figure 1).

For this purpose, a virtual simulation of the NC

machining processes can provide an insight about

the real process conditions. Nonetheless, in the

existing simulation systems neither the process

behavior nor the phenomena occurring during the

process are considered.

2.1 State of the Art in Machining

Simulation

The last decades have seen a number of simulation

approaches being developed specifically for

determination of machining process parameters. The

most common approaches are the finite element

(FEM) based, analytical model based, and

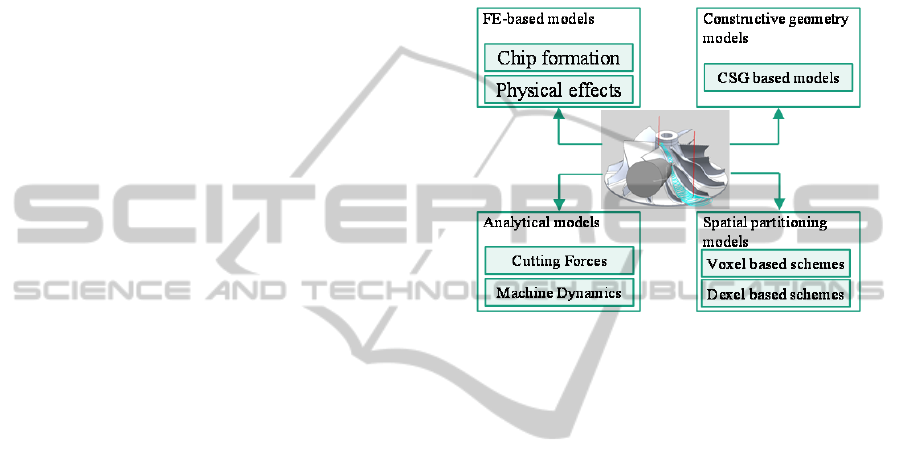
geometrical model based (refer Figure 2).

Constructive Solid Geometry (CSG) based models

and the spatial partitioning models are the most

frequently deployed geometrical models for the

evaluation of the entire NC processes (Zabel, 2010).

The FEM based models are computationally

intensive and possess limited predictive capabilities,

thus their implementation in the milling process

planning is not practical due to the amount of time to

be invested for the calculation efforts. The analytical

model for cutter workpiece engagement cannot be

implemented for freeform surfaces since analytical

model equations are only valid for simplified

workpiece geometry. The geometry based models

focus mainly on the visual aspects of the resulting

geometry deriving very limited access to

technological process quantities.

Figure 2: Overview of existing simulation models for

machining processes. (Minoufekr et al., 2013).

The available milling simulation approaches based

on the dexel and voxel models focus less on the

physical properties. For e.g. Vericut provides

options for collision detection for three and five axis

milling processes (CGTech 2013). The obtained

results in the geometry based models are insufficient

since the modelling approaches are highly

simplified. Minoufekr et al. present a novel

alternative in (ICINCO, 2013), wherein the

macroscopic contact conditions are calculated for

every point on the cutting tool axis for every

toolpath point in the multi-axis milling. The

approach is referred to as macro simulation.

However, the model needs to be extended so that the

engagement on individual cutting edges can be

analysed.

2.2 Modelling of Macroscopic

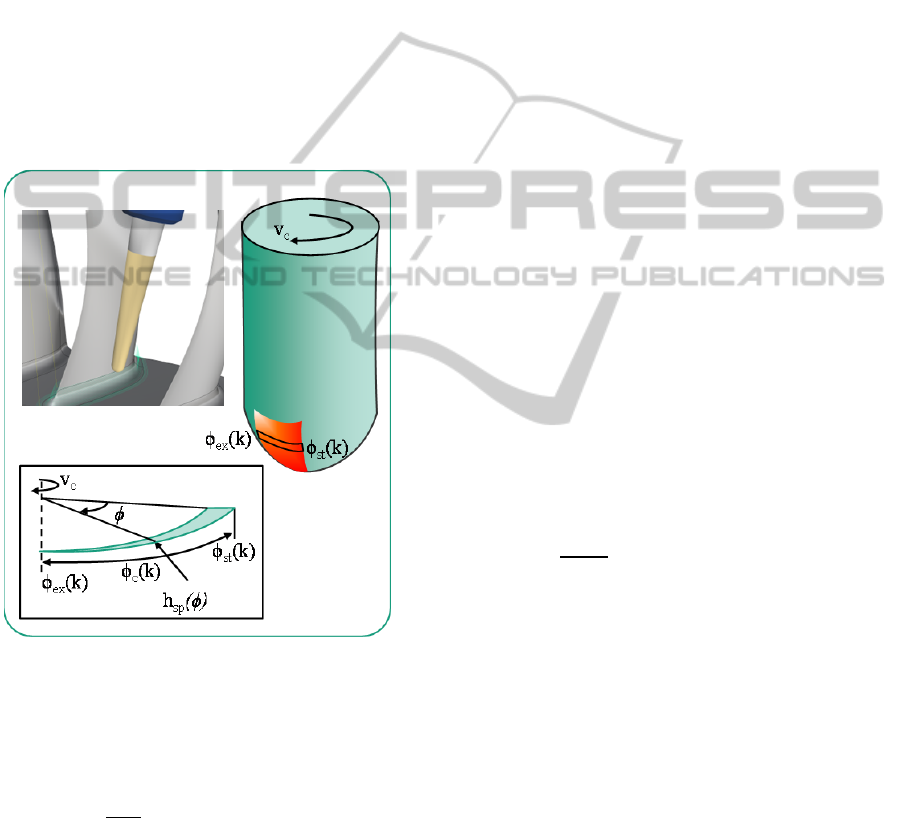
Engagement Conditions

In the macro simulation, a slice model for a cutting

tool is used along with a multi-dexel model for the

workpiece in order to calculate the engagement

conditions along the tool axis at discrete points on

the toolpath. This modelling approach enables an

efficient calculation method for large toolpaths for

multi-axis machining of free-form surfaces. The

contact angle ϕ

is determined using the following

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

662

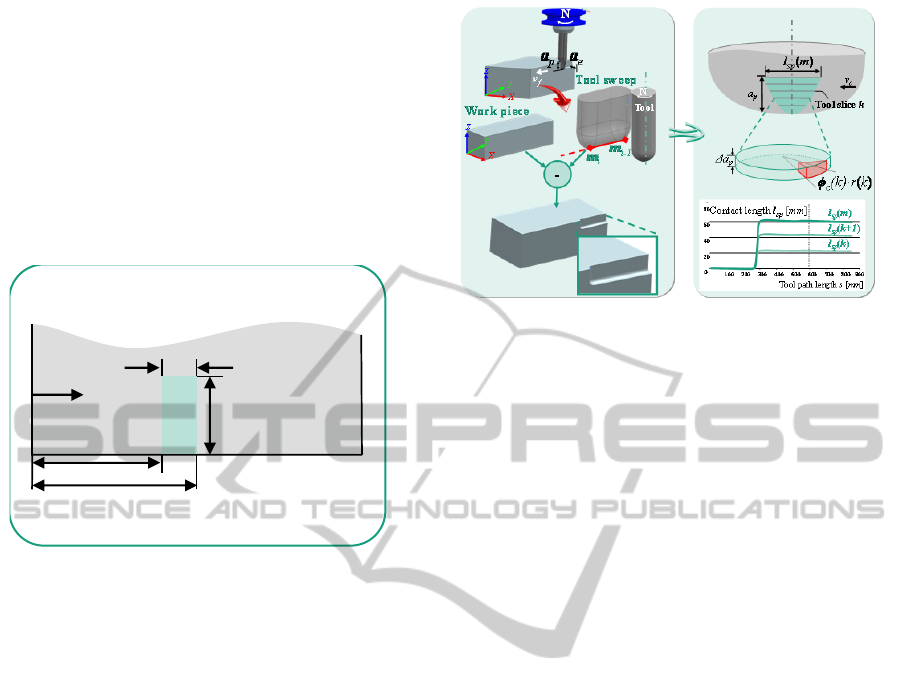
equation:

= ϕ

– ϕ

(1)

where, ϕ

and ϕ

are the entry angle and the exit

angle respectively, as illustrated in Figure 3. The

axial depth of cut is denoted by a

, the cutting tool

radius by r

and the direction of the cutting velocity

and tool rotation by v

. Since the calculation of ϕ

and ϕ

is independent of the cutting edges of the

cutting tool, these quantities are considered to be

macroscopic (Meinecke, 2009).

Figure 3: Macroscopic engagement conditions calculated

in macro-simulation (Meinecke, 2009).

In multi-axis machining, the tool orientation with

respect to the workpiece and the feed direction is

constantly changing along the NC toolpath. Due to

changing engagement conditions, the contact angle

is also varying along the tool axis and along the NC

tool path. This information can prove pivotal in

process evaluation. In order to calculate and use this

information, the cutting tool is discretized in slices

along its axis. Every tool slice is represented by k ϵ

[0, n], n being the total number of tool slices. For

axial slices, height for each tool slice is Δa

. The

contact angle for every tool slice is calculated

considering the surface envelope of the cutting tool

geometry using equation (2):

(k)= ϕ

(k) – ϕ

(k) (2)

Additionally the contact arc length (l

arc

) can also be

calculated according to equation (3):

arc

(k)= ϕ

(k) × r

(k) (3)

where, r

(k) is the radius of the tool slice. On the one

hand, the macro simulation delivers an efficient

approach for fast calculation of the tool workpiece

engagement in multi-axis milling on a high level of

abstraction. On the other hand, the macro simulation

cannot provide information relating to the individual

cutting edges in contact.

Figure 4: Geometric approach for macroscopic

engagement simulation of multi-axis processes.

(Minoufekr et al., 2013).

Due to this fact, direct derivation of the process

conditions is limited in the macro simulation. To

achieve a deeper understanding and to further derive

process characteristics, the goal of the current

research topic is to extend the macro simulation to

obtain detailed information regarding the individual

cutting edges.

2.3 Problem Definition and Research

Question

Multi-axis milling processes are characterized by the

dynamic nature of cutting tool workpiece

engagement. Thus mechanical and thermal load on

the cutting tool are also changing at different points

along the toolpath. Identification of engagement

conditions on the toolpath where unpredictable

mechanical or thermal load leading to tool wear, in a

simulation environment enables to proactively

eliminate the critical process phenomenon and thus

optimize the machining process. Literature review

suggests that mechanical load and thermal load are

proportional to geometrical input variables such as

axial depth of cut (a

), radial depth of cut (a

)

(Klocke, 2011) and contact length of cutting edge

(Bouzakis, 2008) respectively. Minoufekr et al.

established a link between the physical process

quantities for e.g. Force (F

) and the simulated

geometrical process quantities for e.g. the contact

angle (ϕ

) by macroscopic contact conditions

(Minoufekr et al., 2013). The macro simulation

provides a fast model to characterize the NC

machining processes on a higher abstraction level.

Due to this higher level of abstraction, the

capabilities of the macro simulation are limited with

regards to direct calculation of process conditions. In

the macro simulation, the engagement conditions

Macroscopic simulation

ProcessCharacterizationandEvaluationofNCMachiningProcessesbasedonMacroscopicEngagementSimulation

663

regarding the individual cutting edges cannot be

directly calculated which is essential for a deeper

analysis of physical effects on the tool since the

engagement conditions on each cutting edge have a

direct link to cutting forces. Thus an extension of the

existing macro simulation is essential which presents

the research question of this work:

How can the macro simulation be extended so

that the contact per cutting edge can be determined

to characterize and evaluate the multi-axis milling

process?

3 SOLUTION AND METHOD

Macroscopic process characteristics such as the

cutting method can be determined using the macro

simulation result. With the mapping of cutting edge

geometry in the macro simulation, engagement

analysis of individual cutting edges is possible.

From the engagement analysis, the geometrical

parameters for process characterization are

determined. This enables characterization of the NC

machining process based on purely geometric

quantities. Then further the process is evaluated

based on the instantaneous values of the

characterization parameters. This approach is

illustrated in Figure 5.

Figure 5: Proposed approach for process analysis with

macro simulation.

3.1 Directly Derivable Process

Characteristics based on

Macroscopic Engagement

An important parameter during process design is the

selection of the cutting method, i.e. up-milling and

down-milling. C. Gey found that the tool wear in

down-milling is lower as compared to up-milling

(Gey, 2002), also during machining of aerospace

alloys for e.g. titanium alloys and nickel based

alloys, there is formation of chip root in up milling

and hence should be avoided (Klocke, 2011). Thus

identification of the cutting method provides

important insight about the engagement situation.

The cutting method can be directly interpreted from

the result of the macro simulation as illustrated in

Figure 6.

Figure 6: Definition of up-milling and down-milling in

macro-simulation for counter-clockwise rotation.

The direction vectors of cutting velocity v

and the

feed velocity v

are in opposite direction to each

other in the engagement region in up-milling, and

the direction vectors are parallel to each other in the

engagement region in down-milling (Klocke, 2011).

In the macro simulation, the values of the entry

angle ϕ

and the exit angle ϕ

are plotted on the

surface envelope of the cutting tool model on each

tool slice. The position for 0° and 180° is illustrated

in Figure 6 and indicates the direction of

measurement of angles. The tool slice is divided into

four quadrants. The maximum possible contact angle

is 180°. Hence the value of ϕ

cannot exceed

180° and the minimum value of ϕ

is 0°.

NC Process analysis with macro

simulation

Macroscopic simulation

Engagement analysis for

individual cutting edges

Process Characterization

Optimization advice

Process Evaluation

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

664

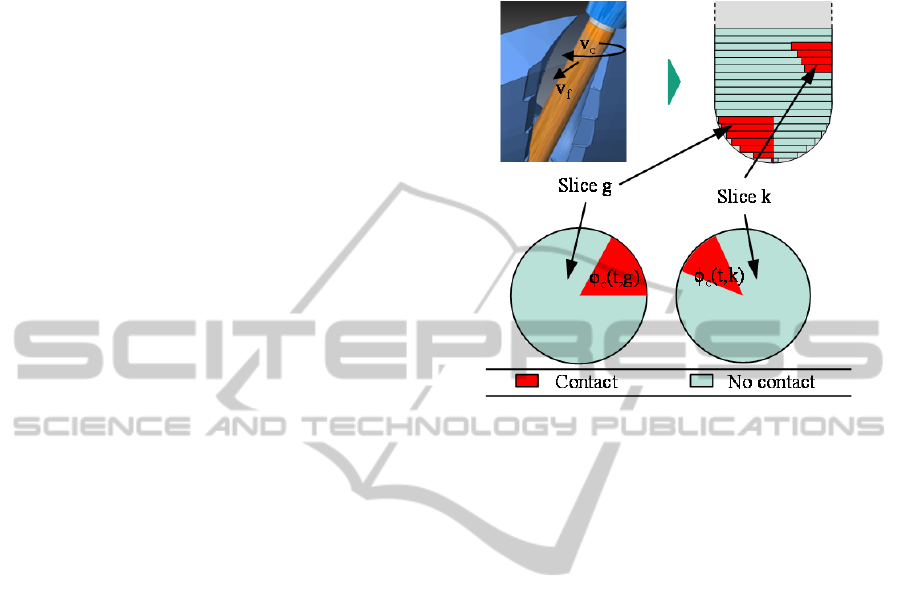
Figure 6

illustrates the definition of up-milling

(a) and down-milling (b) for a cutting tool rotating

clockwise. The contact in up-milling is in the 1

quadrant, and for down-milling is in the 2

quadrant. The sense of rotation in macro-simulation

is recognized from the NC code, M03 for clockwise

rotation (CW) and M04 for counter-clockwise

(CCW) rotation. The engagement region between

the cutting tool and the workpiece lies in the 1

quadrant. The entry angle ϕ

can have the value 0°.

The value of exit angle ϕ

should always be greater

than the entry angle ϕ

. The maximum allowable

value of the exit angle for up-milling is 90°. Hence

the value of the entry angle must be smaller than

90°. If the two values are equal then the contact

angle is zero (refer Equation (1)). Equations (4)-(7)

depict conditional definition for up-milling and

down-milling in macro-simulation for CW and

CCW rotations.

ϵ (90°, 180°]

∧

ϵ (ϕ

°, 90°]

∧

M03 → Up-milling

(4)

ϵ [0°, 90°)

∧

ϵ (ϕ

°, 90°]

∧

M04 → Up-milling

(5)

ϵ [0°, 90°)

∧

ϵ (ϕ

°, 0°]

∧

M03 → Down-milling

(6)

ϵ [90°, 180°)

∧

ϵ (ϕ

°, 180°]

∧

M04 → Down-milling

(7)

For a process designed as up-milling or down-

milling, if the position of the entry angle and the exit

angle are identified as ϕ

ϵ [0°,90°) and

ϵ (90°,180°] respectively and CW rotation, then

there is a transition in the cutting method from up-

milling to down-milling. The identified cutting

method due to such engagement condition is

undefined, and hence should be avoided.

During multi-axis milling of turbine blades,

contact on radially opposite sides on the cutting

length of the cutting tool on different axial positions

is possible. This phenomenon is illustrated in

Figure 7. This leads to simultaneous up-milling and

down-milling. Although the CAM planning software

does not recognise this as an error, because contact

is only in the cutting length region of the cutting

tool, from a process technology point of view, it is a

critical phenomenon. The result is unpredictable

material removal and undefined mechanical load on

the cutting tool. To identify this phenomenon, the

cutting method on each of the tool slices in

engagement is identified. If the cutting method on

any pair of tool slices is inconsistent, i.e. different

cutting methods are identified on the slices in the

pair, simultaneous up-milling and down-milling is

identified. Also, if any slice has two separate

engagement regions, one in the up-milling and the

other in down-milling region, then there is a case of

simultaneous up- and down-milling.

Figure 7: Simultaneous up- and down-milling.

The tip of the ball end mill in engagement during the

process should be avoided (Ozturk, 2009). The

cutting velocity on the ball end mill is increasing on

the spherical part from a value 0 onwards due to

increasing radius along the cutting tool axis. The

zero cutting velocity at the tip results in no material

removal, and a rubbing action when in contact,

resulting in the increase in the temperature at the

cutting tool interface due to friction. In the macro-

simulation the engagement conditions are mapped

on the surface envelope of the cutting tool geometry.

Also the cutting tool is discretized into axial slices,

thus the tip of the cutting tool is contained in the

bottom-most tool slice (k=1). If the contact angle at

the bottommost tool slice is greater than 0° i.e.

(ϕ

(1) > 0°), the tip of the ball end mill is in

engagement.

With the identification of the cutting method,

undefined conditions such as transition of up-milling

to down-milling and simultaneous up- and down

milling can be identified during the CAM planning

stage. Thus resulting in elimination of critical

process conditions and increasing the process

reliability.

3.2 Mapping of Cutting Edge

Geometry in Macroscopic

Engagement Simulation

The mapping of cutting edges in the

ProcessCharacterizationandEvaluationofNCMachiningProcessesbasedonMacroscopicEngagementSimulation

665

macro-simulation enables determination of

engagement conditions for each individual cutting

edge for e.g. the contact length (l

c,i

) and the contact

angle on individual cutting edges (ϕ

c,i

) (refer

Figure 8).

In macro-simulation the engagement conditions

are mapped on the surface envelope of the cutting

tool. The information regarding the contact on the

rake faces of the cutting tool is not derivable (refer

Figure 4). For this reason the geometrical

parameters of the cutting edges which cannot be

mapped onto the surface envelope for e.g. rake

angle, flank angle etc. are not considered. In order to

map the cutting edges in the macro-simulation, two

parameters regarding the cutting edges are

necessary, namely the number of cutting edges Z,

and the helix angle of the cutting edges λ. (refer

Figure 8).

Figure 8: Engagement analysis for individual cutting

edges in the macro simulation result.

The number of cutting edges is given by Z and the

cutting edges are distributed with a constant offset

between consecutive cutting edges, this offset is

called as the angular pitch (ϕ

).it is calculated using

equation (8).

2π

(8)

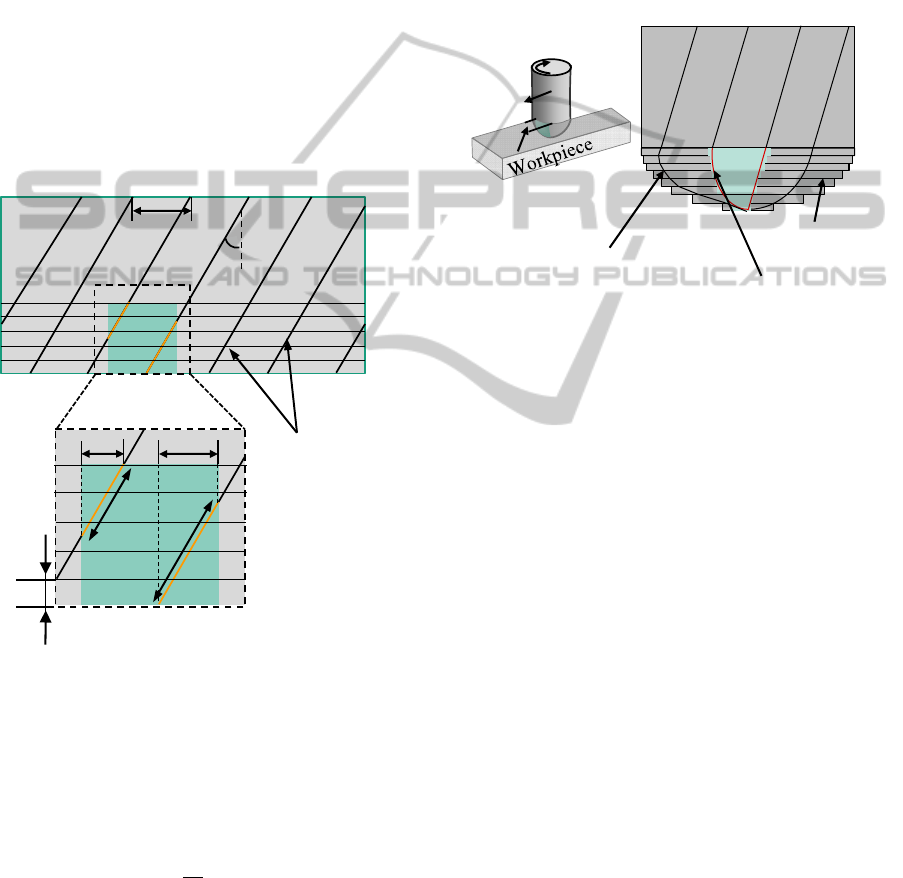
The progression of the helix angle (λ) of the cutting

edges needs to be considered while mapping of

parameters in the macro simulation. The progression

of the helix angle is dependent on the tool shape.

The helix angle of the cutting edges of the

cylindrical end mill is constant along the axis of the

cutting tool, and thus on a 2D developed surface

model for the cylindrical end mill, the cutting edges

are linear (refer Figure 8). The diameter on the

spherical part of the ball end mill is variable along

the tool axis, hence the helix angle of the cutting

edge in case of a ball end mill is not constant along

the tool axis, but defined by a function

(Lazoglu, 2000).

Figure 9: Mapping of cutting edges on a 2D rolled out

model of ball end mill.

The spherical part is divided into slices of constant

diameter and the circumference of each tool slice is

mapped in the 2D rolled out model of a ball end

mill. Also the cutting edges for ball end mill start on

the tip of the ball end mill as illustrated in Figure 9.

The contact angle is assumed to be constant for each

tool slice. The helix angle is calculated for each tool

slice as a function of its axial position, and is

considered to be constant for each tool slice Δa

Hence the cutting edge is mapped as a straight line

on every tool slice. During mapping, the cutting

edges which are in contact can be marked as seen in

Figure 9.

The process condition illustrated in Figure 9 is an

elementary case of engagement between the cutting

tool and the workpiece. This engagement area can be

formally defined and mapped on the surface

envelope of the cutting tool. As illustrated in

Figure 10, the engagement area for a 5-axis milling

case of an impeller is mapped. It can be seen from

the figure that the engagement area is distorted and

cannot be defined formally. Also the contact on

individual cutting edges also cannot be defined

formally. To enable the mapping of the contact for

individual cutting edges, the contact angle calculated

for each tool slice is essential. The contact angle is

z=0

z=a

ϕ=360°

ϕ=0°

Δa

c,3

c,4

c,3

c,4

Cutting

edges

2D rolled out model

Tool slice

Cutting edge in contact

(marked red)

Cutting edge in not contact

3D Model

Cutting tool

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

666

Figure 10: Mapping of microscopic parameters reflecting

contact conditions on a 2D rolled out model of ball end

mill.

then mapped on the tool surface envelope. The

position of the cutting edges mapped in the 2D

rolled out model of a cutting tool is considered to be

constant. Thus comparing the peripheral position of

the cutting edges and the contact angle for each tool

slice, the exact engagement for individual cutting

edge for every position along the cutting tool axis is

determined.

3.2.1 Derivable Microscopic Geometric

Parameters from Macroscopic

Engagement Analysis

With the information regarding the exact contact

conditions on individual cutting edges, geometric

quantities, such as the number of cutting edges in

contact, the contact length (L

) and the uncut chip

geometry parameters such as the chip thickness (h

the and the chip cross section area (A

) can thus be

derived using the result of the macro simulation.

This is achieved by the extension of the macro

simulation as illustrated in Figure 11.

Figure 11: Determination of microscopic parameters in the

macro-simulation.

For a given contact angle ϕ

the contact length on

every tool slice is determined using the equation (9)

where r

is the cutting tool radius.

(k)=

(ϕ

(k)-ϕ

(k))

sin



k

(9)

Six possibilities of contact on the cutting edge

(Altintas, 2012). are illustrated in Figure 12

for tool

slices, where ϕ

1,1

and ϕ

1,2

are the angular positions of

the cutting edges on the cutting tool periphery, the

part of the cutting edge in contact is coloured

orange, and the part not in contact is coloured black.

The exact contact length for each individual cutting

edge on each tool slice dl

(t,k) for every point on the

toolpath can be determined. The contact length l

(t)

for one cutting edge summed over all the tool slices

n is calculated using Equation (10):

t



(

k=1

(10)

The total contact length for all cutting edges L

(t) at

every point on the toolpath is calculated using the

equation (11), where Z is the number of cutting

edges.

Figure 12: Cutting edge contact length for each tool slice.

Macro-simulation result

(k) ϕ

(k)ϕ

(k) r

(k)

Microscopic parameters

Cutting edge geometry

(4)

z=0

z=Δa

z=0

z=Δa

z=0

z=Δa

1,1

1,2

1,1

(5)

(6)

ϕ=360° ϕ=0°

Direction of rotation

1,2

1,1

1,2

(1)

1,1

(3)

Direction of rotation

ϕ=360° ϕ=0°

1,2

1,1

(2)

ProcessCharacterizationandEvaluationofNCMachiningProcessesbasedonMacroscopicEngagementSimulation

667

(t)=



s,j

(t)

j=1

(11)

Figure (13) (a) illustrates a case of blisk machining

with a ball end milling cutter, (b) shows the

engagement field mapped on the tool surface

envelope. The contact angle is variable along the

cutting tool axis. The progression of the chip

thickness is illustrated in part (c) for a tool slice k.

The chip thickness according to Fischer’s approach

is calculated using equation (12). The chip thickness

depends not only on the contact angle ϕ

but also

on the position of ϕ

and ϕ

on the tool periphery.

The chip cross section area (A

) also depends on the

and ϕ

. The chip cross-section area can be

determined using equation (13) (Meinecke, 2009)

respectively.

Figure 13: Progression of chip thickness over the contact

angle.



sin(

(12)





sin

 h







,



,







d

(13)

Where, D is the cutting tool diameter, ϕ

1,j

and ϕ

2,j

are

the angular positions of the entry angle and the exit

angle of the cutting edges. And

is the tool rotation

angle as depicted in Figure 13. From the contact

angle calculated for every tool slice and the cutting

edge helix angle, the progression of the chip

thickness and chip cross section area for each tool

slice can be calculated. This enables determination

of local uncut chip geometry parameters.

The cutting edges enter and leave the

engagement area due to the rotation of the cutting

tool, resulting in the variation of the contact length

and chip cross section area. The rotation of the tool

can be simulated by iterating the values of ϕ

and ϕ

from 0° to 360°, and thus the variation in contact

length of the tool and the chip cross section area at a

point on the tool path can be analysed. This variation

in the values of the geometrical microscopic

parameters can be used for characterization of NC

machining processes based on process technology

values. Moreover, it can be evaluated if the

instantaneous values of the process technology

parameters are exceeding the minimum and the

maximum values decided during process design.

3.3 Process Characterization

Parameter based process characterization

The microscopic geometric quantities related to the

uncut chip determined on the basis of macroscopic

parameters (refer

subsection 3.2.1

), have direct co-

relation to process technology parameters. Due to

which, the magnitude of the microscopic geometric

parameters is indicative of the magnitude of the

process technology parameters for e.g. cutting force

, facilitating the parameter based characterization

of NC machining processes.

The cutting forces F

can be determined using

equation (14):

×K

tanλ







ex,j

st,j

j=1

(14)

where K

is an empirical constant calculated

experimentally and

is the tool rotation angle.

Considering a case of a mould machining process

designed for a constant axial depth of cut, i.e. for

constant tool load, the complex toolpath geometry

results in varying engagement conditions along the

toolpath and thus varying loads. The relation

between the cutting forces and the chip thickness

enables process characterization based on chip

thickness. During process design, an optimal value

of the chip thickness is decided considering the tool

load. On one hand, exceeding of this set optimal

value results in tool overload. Thus the maximum

allowable feed f

z,max

per cutting edge for a point on

the tool path depends on the instantaneous contact

angle, which is dynamically changing. On the other

hand, during chip formation, if the value of feed per

cutting edge f

is too low for the instantaneous

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

668

contact angle, then a chip is never formed, and there

is ploughing effect due to rubbing action between

the cutting tool and workpiece, due to the friction

the temperature at the cutting tool workpiece

interface increases, leading to tool wear (Klocke,

2011). This phenomenon can be identified in the

macro simulation. The minimum allowable value of

feed per tooth, is the one which allows for formation

of chip, i.e. the cutting edge radius (Degner, 1973).

Thus, the value of minimum chip thickness is

constant throughout the process, whereas the value

of minimum feed per tooth f

z,min

is variable along the

toolpath, due to dynamic nature of the changing

contact angle. Any value of the feed per tooth

between f

z,min

and f

z,max

is acceptable but there is loss

in productivity. The conditional equation for

evaluation of processes based on feed per tooth as a

characterization parameter is shown in

equations (15)-(17).

(t) < f

z,min

(t) ∨f

(t) > f

z,max

(t) →

Unacceptable chip thickness

(15)

z,min

(t) < f

z,max

(t) → Acceptable chip

thickness

(16)

(t) = f

z,max

(t) → Optimal chip thickness (17)

During NC machining, multiple cutting edges are in

contact with the workpiece. Due to the rotation of

the cutting tool, the cutting edges enter and leave the

contact region, resulting in the fluctuation of load on

the cutting tool. When a cutting edge exits contact

and at the same moment, another cutting edge enters

contact, there is low fluctuation of cutting forces.

This condition is defined as Uniformity.

Engagement conditions leading to a low fluctuation

in the cutting load are preferred, since this helps in

an optimal process design. Uniformity is defined in

equation (18) (Kronenberg, 1969)











 (18)

where n is an integer, l

arc

the contact arc length and

the angular pitch of the cutting tool. C. Gey

conducted experiments and concluded that when

U=1 there is a local reduction in the cutting forces

(Gey, 2002). There is no variation in the value of

chip cross section area and the contact length.

Uniformity can be used for NC machining process

characterization, as fluctuation in load on cutting

tool is reflected by fluctuation in value of

microscopic geometric parameters. The variation in

chip cross section area (A

) due to tool rotation can

be used as a metric to measure U, given by

equation (19) (Meinecke, 2009).



min







max









(19)

Figure 14: Progression of A

, L

for one cutting edge

with tool rotation.

During milling, when the contact angle for an

individual cutting edge increases as the cutting tool

rotates, the contact length increases linearly,

whereas the increase in chip cross section area is

digressive (refer Figure 14). Thus the contact length

can also be used to measure Uniformity, and to

derive information regarding the process dynamics.

For a cutting tool with multiple cutting edges in

engagement, for one complete rotation, due to the

individual cutting edges entering and exiting the

contact area, the total contact length L

. Thus

equation (20) depicts Uniformity measured on the

basis of the total contact length.



min





max





(20)

4 CONCLUSION

The high manufacturing costs involved in the multi-

axis machining of components having free form

surfaces makes it imperative to meet the highest

0 50 100 150 200

Contact Length L

[mm]

Tool rotation Φ [°]

= 10 mm

Z = 4

λ = 45°

= 44°

= 0.035 mm

0,00

0,02

0,04

0,06

0,08

0100200

Chip cross-section area A

[mm

]

Tool rotation Φ [°]

0.08

0.04

0.00

ProcessCharacterizationandEvaluationofNCMachiningProcessesbasedonMacroscopicEngagementSimulation

669

quality with minimum effort. Moreover, a short

product life cycle leads to frequent design changes.

This increases the challenge on the process designers

to setup fault free processes the first time right. The

macro simulation tool provides an opportunity to

analyse and optimize the machining processes.

In the macro simulation, the macroscopic

engagement is calculated on the discrete points of

the toolpath. Using these calculated macroscopic

engagement conditions, interpretations regarding the

real process conditions can be deduced. With an

extension of the macroscopic simulation, even

microscopic geometric process characteristics are

derived. Thus NC machining processes can be

characterized based on purely macroscopic and

microscopic geometrical parameters which are

derived using the macroscopic engagement

parameters. Further this process analysis is

independent of empirical process data.

Prediction of the critical sections on the toolpath,

where the process technology values can exceed the

allowable limits set during process design, is

possible. Through the proactive identification of the

critical process sections, their elimination at the

process design phase is possible before the

machining processes are executed, thereby reducing

potential expensive damages and machine

downtime. Moreover there is improvement in the

process reliability. Thus there is optimization in the

productivity of the NC machining processes.

ACKNOWLEDGEMENTS

The authors would like to thank the German

Research Foundation DFG for the support of the

depicted research within the Cluster of Excellence

"Integrative Production Technology for High-Wage

Countries".

REFERENCES

Altintas, Y., 2012, Manufacturing automation: Metal

cutting mechanics, machine tool vibrations, and CNC

design, 2nd edn., Cambridge University Press,

Cambridge, New York.

Bouzakis, K.-D., Michailidis, N., Gerardis, S.,

Katirtzoglou, G., Lili, E., Pappa, M., Brizuela, M.,

Garcia-Luis, A. & Cremer, R., 2008, ‘Correlation of

the impact resistance of variously doped CrAlN PVD

coatings with their cutting performance in milling

aerospace alloys’, Surface and Coatings Technology

203(5-7), 781–785.

Choi, B.K. & Jerard, R.B., 1998, Sculptured surface

machining: Theory and applications, Kluwer

Academic, Dordrecht, London.

Degner, W., Ham, N. C., Untersuchungen beim spanen

mit kleinen spanungsdicken, Fertigungstechnik und

Betrieb 13 (1973), 523 – 528.

Gey, C., 2002, Prozessauslegung für das Flankenfräsen

von Titan, VDI-Verl., Düsseldorf.

Hoischen, H., 2003, Technisches Zeichnen: Grundlagen,

Normen, Beispiele, darstellende Geometrie ; ein Lehr-

, Übungs- und Nachschlagebuch für Schule,

Umschulung, Studium und Praxis, 29th edn.,

Cornelsen Girardet, Berlin.

Klocke, F., 2011, Manufacturing Processes, Springer,

Berlin, Heidelberg, New York.

Kronenberg, M., 1969, Grundzüge der Zerspanungslehre:

Theorie und Praxis der Zerspanung für Bau und

Betrieb von Werkzeugmaschinen, 2nd edn., Springer,

Berlin [etc.].

Lazoglu, I. & Liang, S. Y., 2000, ‘Modeling of Ball-End

Milling Forces With Cutter Axis Inclination’, Journal

of Manufacturing Science and Engineering 122(1), 3.

Meinecke, M., 2009, Prozessauslegung zum fünfachsigen

zirkularen Schruppfräsen von Titanlegierungen,

Apprimus-Verl., Aachen.

Minoufekr, M., Glasmacher, L., Adams, O., ‘Macroscopic

Simulation of Multi-axis Machining Processes’, 10th

International Conference on Informatics in Control,

Automation and Robotics (ICINCO 2013), 505–516.

Ozturk, E., Tunc, L. T. & Budak, E., 2009, ‘Investigation

of lead and tilt angle effects in 5-axis ball-end milling

processes’, International Journal of Machine Tools

and Manufacture 49(14), 1053–1062.

Schug, P. et al, 2012, Durchgängige CAx-Prozessketten,

Forschung an der Werkzeugbau Akademie, Apprimus,

Aachen.

Zabel, A., 2010, Prozesssimulation in der Zerspanung,

Vulkan-Verlag, Dortmund.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

670