Characterization of Repeatability of XY-Theta Platform Held by Robotic

Manipulator Arms using a Camera

Anas Hijazi, Jean-Franc¸ois Brethe and Dimitri Lefebvre

Groupe de Recherche en Electrotechnique et Automatique du Havre (GREAH)

Le Havre University, BP540, 76058 Le Havre, France

Keywords:

Robot Precision, Repeatability, Accuracy, Robotic Manipulator Arm, XY-Theta Platform.

Abstract:

This paper presents a XY-Theta micrometric platform, which is extremely compact and offers a wide 300 x

300 mm workspace. This platform is held by a serial kinematic chain of four revolute joints, constituting a

redundant robot. Each point of the horizontal platform can be positioned under a vertical axis in a two-step

approach: in a coarse positioning mode, the four axes are controlled to position and orientate the object with a

position error less than 7 µm; in a ﬁne mode, two axes are mechanically blocked while two others are controlled

to reduce the ﬁnal position error below 2 µm. The choice of the blocked and moving axes depends on the lever

arm length and the mechanism is designed to optimize the link lengths to reduce the ﬁnal position error. The

aim of the paper is to characterize the platform repeatability performances. An estimation of the repeatability

is performed with a camera. These results are then compared to previous results based on the stationary cube

method. The two measurements methods lead to similar results with a repeatability close to 2 µm showing a

signiﬁcant improvement of the performances.

1 INTRODUCTION

Choosing and designing the adequate robot to per-

form a task is not easy. Manufacturers provide some

performance criteria such as payload, workspace di-

mensions, acceleration and repeatability. Most man-

ufacturers advertise that their robot repeatability per-

formances are close to 10 micrometers. These perfor-

mances are generally sufﬁcient to meet most indus-

trial requirements, but it seems that they are difﬁcult

to improve as far as serial robots are concerned. Some

authors claimed that parallel robots could do better

(Merlet, 2006),(Rauf et al., 2004),(Briot and Bonev,

2007) but for the few industrial parallel robots on the

market, the repeatability performances are not better

and the best repeatability is close to 5 µm. For the

XY-Theta platform hold by a parallel robot built in

(Joubair et al., 2012), the repeatability performance

is estimated between 3 and 30 µm depending on the

workspace location.

The estimation of industrial robot precision is

based on a test where the robot is set up to attain a de-

sired point and come back, this cycle being repeated

several times in the same conditions. Measurements

of the ﬁnal robot positions show that they are near the

desired point and all the ﬁnal positions constitute a

cloud of points. Precision is then described in accu-

racy and repeatability as displayed in Fig. 1.

* Accuracy: in the ISO procedure (ISO9283, 1998),

the distance between the mean of the different ﬁ-

nal positions and the target position will character-

ize accuracy. The ANSI deﬁnition (Institute, 1990)

is slightly different as it considers different locations

on a standard path.

* Repeatability: the repeatability index estimates the

closeness of the different points to the cloud center.

Many factors have been suspected to inﬂuence re-

peatability, as speed, load, workspace location, back-

lash, temperature,... Statistical analysis has been per-

formed to discriminate which factor was the most in-

ﬂuent. For example, it was proved that for two 6-axis

serial robot studied, the load inﬂuence was far less im-

portant than the workspace location inﬂuence (Breth

and Dakyo, 2002),(Breth

e et al., 2006). Riemer and

Edan were interested in workspace location inﬂuence

(Riemer and Edan, 2000), Offodile and Ugwu in load

and speed inﬂuence (Offodile and Ugwu, 1991). For

serial robots with revolute joints, it is now clear that

the workspace location is the most important inﬂu-

ence factor. The distance between the target and one

joint axis can show wide variations in the workspace.

The resulting lever arm distance ampliﬁes the joint

421

Hijazi A., Lefebvre D. and Brethe J..

Characterization of Repeatability of XY-Theta Platform Held by Robotic Manipulator Arms using a Camera.

DOI: 10.5220/0005056104210427

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 421-427

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

uncertainty.

Industrial solutions to reach high precision require

the integration of vision systems to control the robot.

But to succeed in the ﬁne positioning, the repeata-

bility performances of the robot must be very good.

We developed a planar redundant structure to improve

precision performances in X and Y directions. This

structure is explained in section 2. In (Breth

e et al.,

2013), we displayed an innovative XY-Theta platform

built in our laboratory that can greatly improve preci-

sion in the whole workspace. This platform will be

described in section 3. The repeatability of this plat-

form was then measured using a hardened steel cube

attached to the vertical axis and one trihedron sup-

porting two Mitutoyo micrometers, ﬁxed on the plat-

form. It was based on the stationary cube method.

This method has though a disadvantage: the mechan-

ical contact between the Mitutoyo micrometers and

the cube can disturb the measurements. The goal of

this paper is to avoid this problem by estimating the

platform repeatability with a camera. When using the

camera, any short or long trajectory could be realized

in the workspace which is not the case when using

the Mitutoyo micrometers. The procedure is based on

the position estimation of an object lying on the plat-

form. The vision system and the steps necessary to

use the vision system as a metrological tool are de-

scribed in section 4: autofocus setup, camera calibra-

tion, image acquisition and processing through the ge-

ometric model ﬁnder toolbox of the Matrox Imaging

Library. In section 5, the platform’s repeatability per-

formances are measured in coarse and ﬁne mode and

the results obtained with the vision system are com-

pared to the stationary cube method. The conclusions

are presented in section 6.

2 INNOVATIVE DISSYMETRICAL

3-LINK ROBOT

2.1 Artiﬁcial Isotropy Point

Our laboratory (GREAH) owns a patent of a 3-link

special redundant manipulator designed to obtain

high precision performances in X and Y directions

(Breth

e, 2009). This innovative robot is presented in

Fig. 2. It consists of a 3-link serial kinematic chain

with three revolute joints. The 1st link length is 30

mm and the 2nd and 3rd link lengths are 120 mm.

This robot is designed to achieve ﬁne positioning near

a speciﬁc point in the workspace. This speciﬁc point

will be named PI ”point of interest”. The procedure

used to obtain the high precision performances is the

Figure 1: ISO approach of accuracy and repeatability.

following:

- a ﬁne positioning is demanded around this point,

so the ﬁnal precision must be ﬁne in two orthogonal

directions. This could be done using two revolute

joints whose rotation centers are as close as possible

to PI. In Fig. 2, it corresponds to the 1st and 2nd axes.

Doing so, an isotropy point is artiﬁcially created in

PI.

- To enlarge the workspace, it is necessary to add a

third axis. Consequently, the robot is able to grasp an

object in a wider area.

Let us study the precision performances. In the

design stage, it is considered that the repeatability and

the resolution of the revolute axes are in the same or-

der of magnitude. For instance, the granularity ratio τ

of the axes is set to τ =

∆

where σ is the standard

deviation of the Gaussian distribution of the angular

position and ∆ is the axis resolution. Considering the

robot structure, the repeatability in PI depends on 3

axes. The third axis angular uncertainty is ampliﬁed

by the third link length. In Fig.3, the blue hexagon

is the uncertainty area characterizing the repeatability

when the 3 axes are controlled and the red square is

the uncertainty area when the 3rd axis is blocked and

only the 1st and 2nd axes are moving. The hexagon

is much larger than the square. More details can be

found in (Brethe, 2010). The idea is then to propose

an innovative control strategy based on a coarse and a

ﬁne mode.

2.2 Coarse and Fine Mode

The control strategy consists of two steps: in a ﬁrst

step, the robot endpoint is brought close to the de-

sired target PI using the three axes. Then the 3rd axis

is mechanically blocked by means of a brake. The

position error is estimated from external sensor infor-

mation and the new target is computed. In the second

step, the robot comes closer to PI using only the 1st

and 2nd axes. This ﬁne positioning is still true if the

ﬁnal point moves away from PI but stays near PI. The

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

422

Figure 2: Innovative planar redundant structure SCARA3

Figure 3: Repeatability depending on moving axes

spatial resolution mesh is slightly changed in orienta-

tion and the square becomes a parallelogram, but the

dimensions of the parallelogram remain small as long

as the ﬁnal point stays in a disk centered on PI.

3 XY-Theta PLATFORM

We designed and prototyped a XY-Theta platform

consisting of a 300 x 300 mm square platform held

by a redundant kinematic chain of four motorized rev-

olute joints. With this design, it is possible to set

the position (X, Y ) and orientation Ω of a workpiece

situated anywhere on the platform. A vertical linear

axis motorized with a stepper motor can hold various

tools, such as measuring or grinding devices, grip-

pers, camera etc. This axis is ﬁxed on the frame. The

location of the tool center in the XY plane lies exactly

at PI (point of interest) (Breth

e, 2011). The prototype

is displayed in Fig. 5.

The platform can be operated in two different

modes as it is explained in section 2:

• The coarse positioning mode uses the four axes.

In this case, the expected repeatability is in the 5-

10 micrometers range, which is equivalent to high

quality industrial SCARA of the same reach.

• The ﬁne positioning mode consists of two steps.

In the ﬁrst step, the part is moved under the verti-

cal axis to point PI with the correct orientation us-

ing the four axes. The 1st axis θ

is set to

where

the lever arms of the 1st and second axis are mini-

mum and identical at PI so that the ﬁnal lever arm

length corresponds to L

× cos(

) =

√

= 20.1

mm and is 6 times shorter than the 2nd or 3rd arm

lengths of 120 mm. Then, in the second step, the

3rd and 4th axes are mechanically blocked using

the brakes and the positioning error can then be

reduced moving only the 1st and 2nd axes. The

choice of the blocked and moving axes depend

on the lever arm length and the mechanism is de-

signed to optimize the link lengths to reduce the

ﬁnal error. If the platform is considered to be the

entire workspace, all points of the workspace can

beneﬁt from the high precision performance.

Figure 4: Diagram of the XY-Theta platform Kinematics.

4 SETTING UP THE CAMERA TO

ESTIMATE THE

REPEATABILITY

The camera chosen for the vision system is a Basler

acA1600-20gm/gc with a telecentric imaging optics.

This optics is useful to reduce the distortion during

image acquisition. This camera is displayed in Fig. 5.

The connection to the computer is done with Ethernet

protocol. The camera has a high resolution of 1628 ×

CharacterizationofRepeatabilityofXY-ThetaPlatformHeldbyRoboticManipulatorArmsusingaCamera

423

Figure 5: Micropositioning platform: general view.

1236 Pixels, a small vision ﬁeld dimension of 7.1 ×

5.4 mm, a pixel size of 4.4 ×4.4µm and it is located

approximately 65mm above the platform. The 25 ×

25 mm calibration grid displayed in Fig. 6 is used to

calibrate this camera. It is a grid of small dots with a

0.0625 mm diameter, a inter space of 0.125 mm and a

thickness of 2 mm.

Figure 6: The calibration grid.

Four steps are necessary to use the camera as

a metrological tool to estimate repeatability. These

steps are detailed below.

4.1 Acquisition and Image Processing in

the Matrox Imaging Library (MIL)

MIL (mat, 2008) offers several toolboxes and func-

tions for image processing. First, the MIL is used to

load one image from the camera and store it for fur-

ther processing. A clear image is needed and for this

purpose the focus must be set properly. An autofocus

procedure is implemented as detailed below.

4.2 Autofocus of the Vision System

An autofocus procedure using the MIL functions is

proposed. The goal is to ﬁnd automatically the opti-

mal distance between the camera and the calibration

grid for optimal contrast. The camera is ﬁxed on a

motorized linear vertical axis as displayed in Fig. 7.

Figure 7: The camera and the calibration grid.

The camera is controlled to move slowly in an in-

terval of 0.25 mm. Meanwhile images are acquired

and stored. The contrast of each image is then com-

puted. The contrast is an intrinsic property of an im-

age that refers to and quantiﬁes the difference be-

tween the light and dark parts of an image. The

contrast is here calculated by the Root Mean Square

(RMS) (Peli, 1990) which is deﬁned as the standard

deviation of pixel intensities:

RMS =

M.N

N−1

∑

i=0

M−1

∑

j=0

i j

−I)

(1)

Where:

• Intensities I

i j

are the i

and j

element of the two

dimensional image of size M by N.

• M ×N is the resolution of the Image.

• I is the average intensity of all pixels values in the

image.

In the experimental setup, 20 images are captured

from several heights and the optimal height corre-

sponding to the maximum contrast is computed.

The image with maximum contrast is obtained but

its unit is in pixel and not in millimeters, so the im-

age has to be calibrated to obtain its coordinates in

millimeters (Tamadazte et al., 2009), (Ammi et al.,

2005), (Zhou and Nelson, 1999).

4.3 Camera Calibration

The objective of camera calibration is to determine all

the parameters necessary to predict the image pixel

coordinates (r, c) of the projection of a point in the

camera’s ﬁeld of view, given that the coordinates of

that point with respect to the world coordinate frame

are known (Tamadazte et al., 2009),(Ammi et al.,

2005),(Zhou and Nelson, 1999). In other words,

given the coordinates of P relative to the world coordi-

nate frame, the coordinate in mm could be read. After

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

424

performing the calibration, this ﬁle could be saved as

a calibration object and stored as a model. To cal-

ibrate another image, it is sufﬁcient to allocate this

model to the calibration object already saved in MIL.

4.4 Geometric Model Finder (GMF)

Before measuring repeatability, we must understand

how to deﬁne a pattern in the image and be able to

determine the difference of position of the pattern in

two different images.

MIL includes a tool for performing pattern recog-

nition that it is primarily used to locate complex ob-

jects for guiding a gantry, stage or robot, or for pro-

cessing measurement operations. This tool named

Geometric Model Finder (GMF) tool is based on a

patented technique that uses geometric features and

contours to ﬁnd an object.

In our case, a pattern of about 1 ×1 mm dimen-

sions is chosen, this pattern is engraved on a metal

sheet and an arbitrary letter (e) is chosen as a model

as displayed in Fig. 8 but it is of course possible to

choose any letter as model. The small square around

the letter shows that it is the model with 130 × 120

Pixels and the large square corresponds to a fraction

of the camera vision ﬁeld 640 ×480 Pixels.

Figure 8: The model chosen to estimate repeatability.

MIL computes directly the coordinates of the cen-

ter of gravity of a selected pattern. Moreover when

the image is calibrated, these coordinates are given in

millimeters.

5 REPEATABILITY

PERFORMANCES AND

DISCUSSION

5.1 Repeatability Performances in

Coarse Mode

In this repeatability estimation, the four axes are mov-

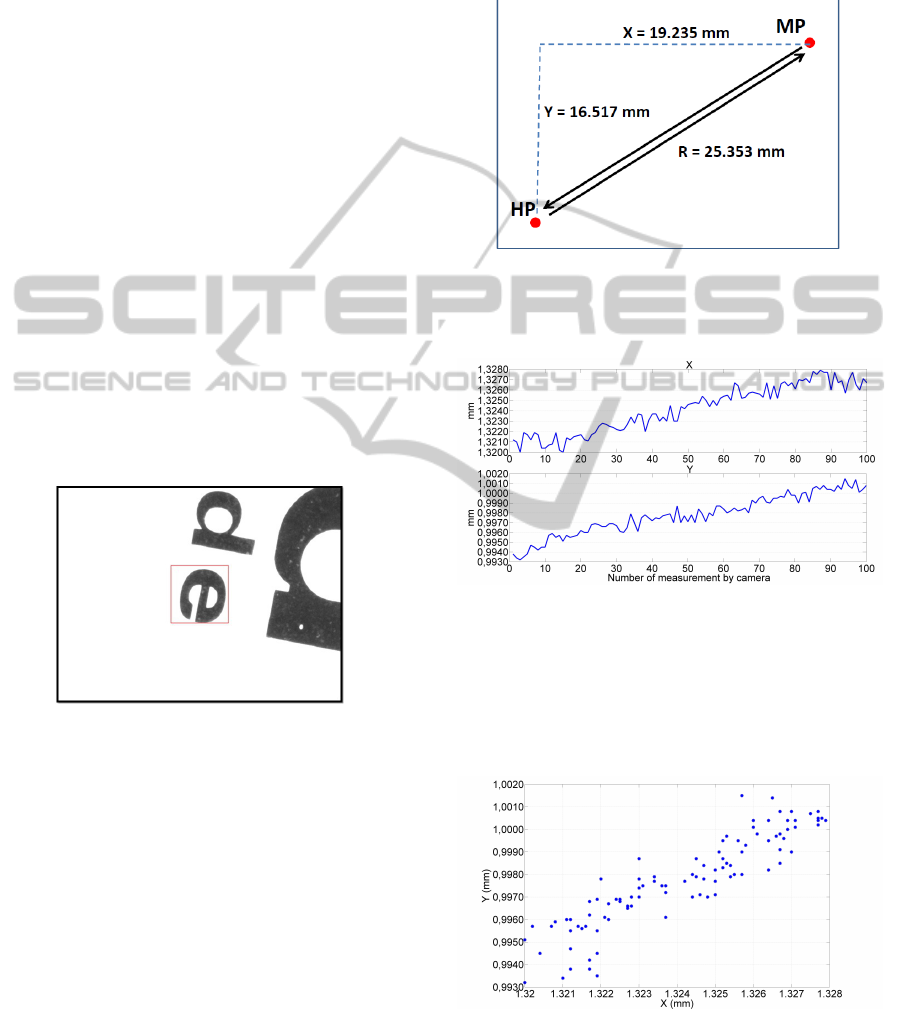
ing. The harmonization point (HP) is set 25.353 mm

away from the measurement point (MP). The target

is brought at the PI (point of interest), the position is

measured, then the tool moves to harmonization point

(HP) and the cycle is repeated 100 times. This trajec-

tory is displayed in the Fig. 9.

Figure 9: Trajectory which is carried out in coarse mode.

The resulting XY positions of the (MP) are dis-

played in Fig. 10.

Figure 10: XY ﬁnal position at MP when all axes are mov-

ing.

The width of the X and Y ﬁnal position interval

is between 7 and 8 micrometers. The computation of

the ISO repeatability based on the 100 sample leads

to a performance of 7.0µm. The corresponding cloud

of points is displayed in Fig. 11.

Figure 11: The cloud of points when arriving to MP in

coarse mode.

CharacterizationofRepeatabilityofXY-ThetaPlatformHeldbyRoboticManipulatorArmsusingaCamera

425

5.2 Repeatability Performances in Fine

Mode

The harmonization point (HP) is set 2.331 mm away

from the measured ﬁnal position. The (MP) is brought

at the PI, the position is measured, then the harmo-

nization point is brought at the PI, and the cycle is

repeated 100 times. In this repeatability estimation,

only the ﬁrst and second axes can move, the other axes

being mechanically blocked with the brakes. This tra-

jectory is displayed in the Fig. 12.

Figure 12: Trajectory which is carried out in ﬁne mode.

The resulting X and Y ﬁnal positions at MP in

ﬁne mode when 3rd and 4th axes are blocked are dis-

played in Fig. 13.

Figure 13: XY ﬁnal positions at MP when 3rd and 4th axes

are blocked.

The maximum width of the X and Y ﬁnal position

interval is between 2 and 4 micrometers. The compu-

tation of the ISO repeatability based on the 100 sam-

ple leads to a performance of 2.1µm. The correspond-

ing cloud of points is displayed in Fig. 14.

5.3 Discussion

In this paper, the vision system is used to estimate

repeatability, no mechanical contact occurs with the

robot. The repeatability in coarse mode is 7µm and in

ﬁne mode is 2µm.

Figure 14: The cloud of points arrived in X and Y directions

at MP in ﬁne mode.

It is worth mentioning that a larger measuring

campaign has been performed. Ten more trajectories

have been tested all around the workspace of 300 ×

300 mm. The results of these several tests lead to the

same conclusion.

In (Breth

e et al., 2013), the platform repeatability

performance was estimated with the stationary cube

method. The measurement device was using two Mi-

tutoyo micrometers with a resolution of one microm-

eter. The hardened steel cube was held by the verti-

cal axis. The Mitutoyo micrometers were on the plat-

form. In this method, there is a mechanical contact

between the micrometers and the hardened steel cube.

A general view of this measurement system is given

in Fig. 15. The repeatability in coarse mode was4µm

and in ﬁne mode it was 2µm.

Figure 15: Measuring with the Mitutoyo micrometers.

When comparing the repeatability estimation with

the two measuring systems, we notice that for the ﬁne

mode, the repeatability performance is nearly identi-

cal. On the other hand concerning the coarse mode,

the non-contact measurement system gives a global

estimation worst than the contact measurement sys-

tem. In fact, when using the Mitutoyo micrometers,

the maximum trajectory length is about 5 mm to keep

a constant contact between the micrometers and the

robot. But, when using the camera, any short or long

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

426

trajectory could be realized in the workspace. So

larger trajectories can be tested, for instance, some

trajectory lengths are about 25 mm. The possibility

to make the platform move along longer trajectories

is a major advantage of the measuring system based

on the camera compared to our previous measuring

method. But if the trajectory is longer, it makes sense

that the repeatability performance is lower. Another

advantage of the camera versus the mechanical mea-

suring system is its ﬂexibility and easy implementa-

tion.

6 CONCLUSIONS

In this paper, the XY-Theta Platform is presented, de-

signed with the same mechanical and control compo-

nents of usual industrial robots. But based on a spe-

ciﬁc design and control, this platform improves re-

peatability performances signiﬁcantly. The repeata-

bility performances of this platform have been previ-

ously estimated using the stationary cube method. In

this paper, another method based on a vision system is

used to compute the repeatability performances. The

results of these two methods all point in the same di-

rection: the repeatability in the ﬁne positioning mode

is close to 2µm when the repeatability in the coarse

positioning mode is close to 4 −7µm.

More studies will be performed on this plat-

form. For instance, the platform performances con-

cerning orientation repeatability of the workpiece are

now been investigating. Another scientiﬁc interest-

ing topic is the study of the singularities locations in

the workspace, dealing with redundancy and singu-

larities when planning a trajectory from (X

, Y

, Ω

)

to (X

, Y

, Ω

The GREAH laboratory is now looking for part-

ners to develop these concepts in industrial or aca-

demic applications with high precision performances.

REFERENCES

(October 20, 2008). Matrox Imaging Library (MIL).

Ammi, M., Fremont, V., and Ferreira, A. (Barcelona, Spain,

avril, 2005). Flexible microscope calibration using

virtual pattern for 3-d telemicromanipulation. In IEEE

International Conference Robotics and Automation.

Breth

e, J.-F. (2009). Manipulator robot and associated

control for ﬁne positioning of the terminal end.

PCT/FR2009/00459, Patent.

Brethe, J.-F. (2010). Innovative kinematics and control

to improve robot spatial resolution. In IROS, pages

3495–3500.

Breth

e, J.-F. (2011). High precision motorized micrometric

table. FR2011/02184, Patent.

Breth

e, J.-F. and Dakyo, B. (2002). A stochastic ellip-

soid approach to repeatability modelisation of indus-

trial robots. In IROS, pages 1608–1613.

Breth

e, J.-F., Hijazi, A., and Lefebvre, D. (2013). Innova-

tive xy-theta platform held by a serial redundant arm.

ECMSM, pages 146–151.

Breth

e, J.-F., Vasselin, E., Lefebvre, D., and Dakyo, B.

(2006). Modelling of repeatability phenomena us-

ing the stochastic ellipsoid approach. Robotica,

24(4):477–490.

Briot, S. and Bonev, I. A. (2007). Are parallel robots more

accurate than serial robots ? CSME Transactions,

31(4):445–456.

Institute, A. N. S. (1990). American National Standard for

Industrial Robots and Robot Systems - Point-to-Point

and Static Performance Characteristics -Evaluation,

R15.05-1-1990. ANSI.

ISO9283 (1998). Manipulating Industrial Robots - Perfor-

mance criteria and related test methods. ISO.

Joubair, A., Slamani, M., and Bonev, I. A. (2012). A novel

xy-theta precision table and a geometric procedure for

its kinematic calibration. Robotics and Computer-

Integrated Manufacturing, 28:57–65.

Merlet, J.-P. (2006). Parallel Robots. 2nd Ed. Springer.

Offodile, O. F. and Ugwu, K. (1991). Evaluating the effect

of speed and payload on robot repeatability. Robotics

and Computer-Integrated Manufacturing, 8:27–33.

Peli, E. (1990). Contrast in complex images. Journal of the

Optical Society of America, A 7 (10):20322040.

Rauf, A., Kim, S.-G., and Ryu, J. (2004.). A new measure-

ment device for complete parameter identiﬁcation of

parallel manipulators with partial pose measurements.

The Chemnitz Parallel Kinematics Seminar, pages 89–

106.

Riemer, R. and Edan, Y. (2000). Evaluation of inﬂuence

of target location on robot repeatability. Robotica,

18:443–449.

Tamadazte, B., Dembl, S., and Piat, N. L.-F. (March, 2009).

A multiscale calibration of a photon video microscope

for visual servo control. Application to MEMS Mi-

cromanipulation and Microassembly, In Sensors and

Transducers Journal (special issue in Robotic and

Sensors Environments), 5:37–52.

Zhou, Y. and Nelson, B. J. (september,1999). Calibration of

a parametric model of an optical microscope. Optical

Engeenering, 38 (12).

CharacterizationofRepeatabilityofXY-ThetaPlatformHeldbyRoboticManipulatorArmsusingaCamera

427