Self-calibration of Large Scale Camera Networks

Patrik Goorts, Steven Maesen, Yunjun Liu, Maarten Dumont, Philippe Bekaert and Gauthier Lafruit

Hasselt University - tUL - iMinds, Expertise Centre for Digital Media

Wetenschapspark 2, 3590 Diepenbeek, Belgium

Keywords:

Calibration, Feature Matching, Multicamera Matches, Outlier Filtering.

Abstract:

In this paper, we present a method to calibrate large scale camera networks for multi-camera computer vi-

sion applications in sport scenes. The calibration process determines precise camera parameters, both within

each camera (focal length, principal point, etc) and inbetween the cameras (their relative position and orien-

tation). To this end, we ﬁrst extract candidate image correspondences over adjacent cameras, without using

any calibration object, solely relying on existing feature matching computer vision algorithms applied on the

input video streams. We then pairwise propagate these camera feature matches over all adjacent cameras us-

ing a chained, conﬁdent-based voting mechanism and a selection relying on the general displacement across

the images. Experiments show that this removes a large amount of outliers before using existing calibration

toolboxes dedicated to small scale camera networks, that would otherwise fail to work properly in ﬁnding

the correct camera parameters over large scale camera networks. We succesfully validate our method on real

soccer scenes.

1 INTRODUCTION

In the current multimedia landscape, entertainment

delivery in the living room is more important than

ever. Users expect more and more impressive con-

tent to stay entertained. Therefore, new technologies

have been developed, such as 3D television, graphical

effects in movies, interactive television, and more.

We will focus on a single use case of novelcontent

creation, i.e. computer vision applications in soccer

scenes. In this application, a large number of cam-

eras are placed around the ﬁeld, creating a large scale

camera network. These cameras are then used to gen-

erate novel virtual viewpoints (Goorts et al., 2014) or

create tracking information of the players on the ﬁeld.

To make such applications possible, the cameras

should be geometrically calibrated, i.e. their intrin-

sic properties (focal length, principal point, etc) as

well as their relative position and orientation (extrin-

sic parameters) should be estimated (Hartley and Zis-

serman, 2003, page 178). For small scale camera net-

works many approaches exist for intrinsic and extrin-

sic calibration under controlled conditions. Most of

them work by moving calibration objects in front of

the cameras, such as checker board patterns (Zhang,

2000) and laser lights (Svoboda et al., 2005), pro-

viding corresponding feature points in the respective

camera views for extracting intrinsics and extrinsics,

as explained in section 3.

In this paper, we will present a system to calibrate

a large scale camera network placed around the pitch

of a sport scene, here demonstrated in a soccer game.

We demonstrate our method using eight cameras, but

any arbitrary number of cameras can be used. Be-

cause access to the pitch is restricted and the scale is

very large, we will present a self-calibration system

that does not use any calibration objects, such as the

methods of (Ohta et al., 2007) and (Grau et al., 2005).

The main contribution of this paper is the gen-

eration of reliable multicamera image correspon-

dences with a minimum of outliers, for efﬁcient self-

calibration. This avoids a calibration recording pro-

cess, reducing cost and effort. These correspondences

are used in calibration toolboxes intended for small

scale camera networks. We use the toolbox of (Svo-

boda et al., 2005) for estimating the intrinsic and ex-

trinsic parameters.

Correspondence determination and matching is

typically used between two images. Features are de-

tected out of each image separately, and their statisti-

cal descriptors are pairwise matched between two im-

ages. This will, however, not sufﬁce for our applica-

tion, where feature matches between multiple images

are required. Therefore, we present a system to gener-

ate multicamera matches by propagating the matches

between successive pairs of images.

107

Goorts P., Maesen S., Liu Y., Dumont M., Bekaert P. and Lafruit G..

Self-calibration of Large Scale Camera Networks.

DOI: 10.5220/0005057201070116

In Proceedings of the 11th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2014), pages 107-116

ISBN: 978-989-758-046-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b)

Figure 1: Two possible camera arrangements for soccer

scenes. Both arrangements have different properties. (a)

In the linear arrangement, all cameras are placed on a line

next to the long side of the pitch and have the same look-at

angle. (b) In the curved arrangement, all cameras are placed

around a corner of the pitch and point to a spot in the scene.

These multicamera matches might, however, be

unreliable. Therefore, we also present a ﬁltering ap-

proach that is speciﬁcally tailored to cameras placed

next to each other, without a relative rotation around

their optical axes. Even large scale, curved cam-

era pathways can be properly handled by following a

piecewise linear approach over each triple of adjacent

camera views. We remove many outliers that would

not be removed with existing calibration tools, effec-

tively improving the calibration quality.

There are a number of existing camera calibration

methods available for outdoor sport scenes that do not

use calibration objects. Most of these methods use the

lines of the soccer area to determine camera locations

(Farin et al., 2003; Farin et al., 2005; Li and Luo,

2004; Yu et al., 2009; Hayet et al., 2005; Thomas,

2007). They are therefore only applicable if the scene

is a soccer pitch, where the lines are planar and visible

over all camera views. This is, however, not always

the case. The pitch is seldom a plane and cameras

with a small ﬁeld of view do not always have lines in

their image stream. We therefore propose a solution

without this planar line assumption, which makes our

large-scale calibration solution more robust and more

widely applicable, with good self-calibration perfor-

mances (i.e. not requiring any speciﬁc calibration ob-

ject).

The rest of the paper is structured as follows. Sec-

tion 2 describes the used camera setup, with its geo-

metrical properties recorded into camera matrices, as

explained in section 3. Section 4 discusses the gen-

eration of the multicamera correspondences and their

propagation over adjacent cameras. Finally, section

5 describes our multicamera ﬁltering approach to fur-

ther dismiss apparant outliers.

2 CAMERA SETUP

We do not present a camera calibration method for

Figure 2: The projective camera model. A camera center

and an image plane is deﬁned. The image is formed by con-

necting a line between the camera center and the 3D point.

The intersection between this line and the image plane de-

ﬁnes the position of the projection for that 3D point.

all possible camera setups. Instead, we will present a

camera method for a large scale camera network, with

the following properties.

We considered two possible arrangements for the

cameras: a linear arrangement and a curved ar-

rangement with piecewise linear properties over large

scales. These camera topologies are shown in Fig-

ure 1. In both arrangements, the cameras are placed

around the pitch at a certain height to allow an

overview of the scene. Both the curved and linear ar-

rangement use cameras with a ﬁxed location and ori-

entation. Some overlap between the camera images is

required to allow feature matching. Overlap between

every camera is, however, not required.

Our method requires that the cameras are synchro-

nized at shutter level, i.e. all cameras take an image at

the exact same time stamp. To provide this, we use

a pulse generator that periodically transmits a trigger-

ing pulse to all cameras at the same time.

3 REPRESENTATION OF

CAMERA PARAMETERS

In this section, we giveanoverviewof projectivecam-

eras and their matrix representations, commonly used

in computer vision applications.

A simple pinhole camera maps each 3D scene

voxel to a corresponding 2D image pixel, through

projection along the light rays traversing the pinhole.

Any real camera with a lens and ﬁnite aperture fol-

lows this basic voxel-to-pixel mapping principle and

can hence conveniently be modeled by an equivalent

pinhole camera. We will assume that all cameras fol-

low the pinhole projective camera model, as deﬁned

by (Hartley and Zisserman, 2003, page 6) and shown

in Figure 2.

This projective process can be mathematically

represented in matrix notation as follows. Consider

a 3D point χ, represented in homogeneous coordi-

nates. In essence, homogeneous coordinates repre-

sent a point χ = [X,Y,Z]

, using four coordinates χ =

[WX,WY,WZ,W]

withW 6= 0 or χ = [X,Y, Z,1]

. A

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

108

Figure 3: Intinsic and extrinsic camera matrices explained.

The point χ and the camera center are deﬁned in an arbitrary

coordinate system. Multiplying by M will transfer the cam-

era to the origin of the coordinate system, and χ will have

the same relative position. Multiplying by K will project χ

to the image plane.

projective camera now transforms this 3D point χ in

a homogeneous 2D point x = [x,y,1]

using a projec-

tion matrix P:

x = Pχ ⇔









= P













Here, the projection matrix P can be split up in

two sets of components: intrinsic and extrinsic pa-

rameters, represented by the intrinsic matrix K and

the extrinsic matrix M, with P = KM.

The intrinsic camera parameters represent the re-

lation between a 2D pixel location and its correspond-

ing 3D ray, presuming the camera is placed at the ori-

gin, and the image plane is parallel to the XY plane

at Z = f, where f is the focal distance. The line per-

pendicular to the image plane and passing through the

center of projection is called the principal axis, while

the point where the principal axis intersects the image

plane is called the principal point. The principal point

can be represented as a 2D point (p

, p

) on the image

plane. The 3× 3 matrix K is then given by:

K =





f 0 p

0 f p

0 0 1





Using x = Kχ for a camera placed at the origin

with an image plane Z = f, x is the image coordinate

on the image plane with principal point (p

, p

However, the camera is seldomly placed at the

origin, especially if multiple cameras are involved.

Therefore, the 3×4 extrinsic matrix M is used, which

transforms 3D voxels to a new location and orienta-

tion, so that the intrinsic matrix K is applicable (Hart-

ley and Zisserman, 2003, page 155). The matrix M

consists of a rotation and a translation, as shown in

Figure 3, and has the following form:

M =



R −R



where R is a 3 × 3 rotation matrix and

C is the

camera location in non-homogeneous coordinates.

In essence, M will translate and rotate the world

such that the camera is placed at the world origin,

where K will then project the 3D voxels to the image

plane, resulting in the ﬁnal, projected image.

Using this camera model, the calibration process

then consists of determining these projection matri-

ces, when only the images of the cameras are given.

To this end, we acquire image correspondences using

feature matching, use them to generate the projection

matrices, and then ﬁnally split these projection matri-

ces into their intrinsic and extrinsic components using

the QR decomposition (Hartley and Zisserman, 2003,

page 579), which exploits the triangular shape of ma-

trix K.

4 DETERMINATION OF 2D

IMAGE CORRESPONDENCES

We determine image point correspondences by us-

ing a feature detector on all synchronously captured

images individually, followed by all possible combi-

nations of pairwaise matching. To increase robust-

ness, feature matching between each pair of images is

done in two directions, i.e. ﬁnd the matches from im-

age 1 to image 2, and cross-check with the matches

from image 2 to image 1. A number of pairwise fea-

ture detectors were tested (Doshi et al., 2010), includ-

ing the SIFT (Lowe, 2004) and SURF (Bay et al.,

2006), where SIFT proved to provide the most reli-

able matches on our dataset.

The conﬁguration of the cameras determine the

exact approach for ﬁnding matches. If the cameras

are far away from each other, only groups of three se-

quent cameras are considered to ﬁnd matches. This

avoids extreme outliers resulting from matches over

images that contain a very different part of the scene.

If the cameras are placed in an arc, one camera can

have a view angle perpendicular to the view angle of

another camera. This will make matching of features

on players unreliable and is therefore avoided by us-

ing only three successive cameras.

If the cameras are close to one another and there

is a large overlap between all cameras, matches be-

tween all pairs of images are searched for. We will

select matches between all cameras using a consen-

sus based searching approach.

For a multicamera match to qualify for use in cali-

bration, it has to contain features of at least three cam-

eras and the matching in each image pair has to be

Self-calibrationofLargeScaleCameraNetworks

109

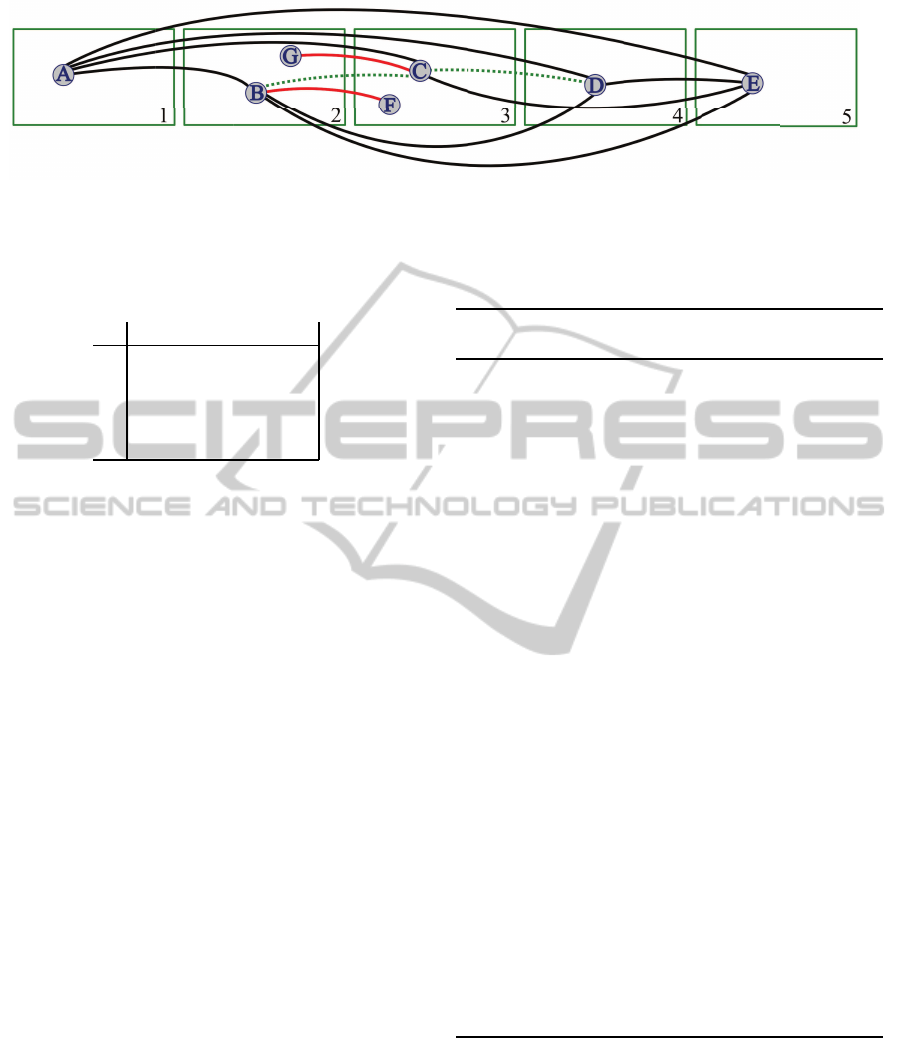
Figure 4: The graph used in our example. Nodes A - G are features detected in a set of images, each of which is taken by a

different camera at the same moment. The red edges show mismatches between features, the black correct matches between

features. The green, dashed lines show the feature matches that should have been found, but were not. After running our

algorithm, A, B, D, E are considered as accepted in the multicamera feature match; C, F, G are rejected.

From Camera

1 2 3 4 5

To camera 1 - A A A A

2 B - G B B

3 C F - - C

4 D D - - D

5 E E E E -

Figure 5: Resulting matrix of the example in Figure 4.

consistent, using the algorithm proposed in the next

paragraphs. An overview of the algorithm is given in

Algorithm 1.

The algorithm can better be explained using the

example of Figure 4. Here, a graph is shown, where

each node is a feature, belonging to a speciﬁc camera

image, and each edge represents matching features in

two directions. An edge between node A and B, cor-

responds to a match between feature A and feature B,

and vice versa.

We consider every pair of images and decide

which feature pair will be kept, and which will be

discarded. We decide which other features in other

images belong to this match, therefore creating a mul-

ticamera match. For example, we consider camera 1

and camera 2. One of the cameras is the primary cam-

era C

, the other is the subordinate camera C

. We

choose camera 1 as C

. Next, we construct a feature

cross check matrix for each feature F

that is a part

of a match between C

and C

. In our case, we con-

sider feature A. The matrix consists of N rows and

N columns (where N is the number of cameras) and

each row and column corresponds to a camera image.

We now complete every element of the matrix.

For each element there is a “from” camera C

and a

“to” camera C

. First, we select the match from C

, that is C

↔ C

, and use this feature to ﬁnd the

match to C

↔ C

). For C

= 1 with feature A,

= 4 and C

= 5, this would result in A ↔ D and

D ↔ E. The result is the ﬁnal feature from the sec-

ond match, and is placed in the matrix on row C

and

column C

. If there is no match, or if C

= C

, the

Algorithm 1: Overview of the multicamera feature match-

ing and selection algorithm.

Create empty list of multicamera matches L

for all Cameras C

, C

6= C

for all Feature F

↔ F

of C

↔ C

Construct matrix M

for all Cameras C

if c

= c

then

M[C

][C

] = unset

else if c

= c

then

Match F

↔ F

in C

↔ C

M[C

][C

] = F

else

Match F

↔ F

in C

↔ C

Match F

↔ F

in C

↔ C

M[C

][C

] = F

end if

end for

Create empty list of features L

for all Rows in M do

Select most occuring feature F

if Occurrence of F

≥ N/3∗ 2 then

Add F

to L

end if

end for

if L

has at least 3 features then

Add L

to L

end if

end for

position in the matrix is left empty. For our example

in Figure 4, this results in the matrix shown in Figure

There are several important elements worth notic-

ing. First, as shown in Figure 4, there is no match

between C and D, while there is a match A ↔ C and

E ↔ C, and a match A ↔ D, B ↔ D, and E ↔ D.

Therefore, we can conclude that the match between C

and D should exist (as indicated by the dashed green

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

110

Figure 6: Example of multicamera feature matching using 3 cameras. All pairwise features are connected with each other

using lines. Only a subset of the muticamera matches are shown, and the red mismatches will be removed later on in section

edge) and is just not found by the matching algorithm.

Second, B matches to F, but both A and E match to

both B and C. Furthermore, D matches to B. There-

fore, we conclude that the match from B to F is a mis-

match and should be eliminated. The same is true for

G ↔ C. These two cases are handled by selecting the

most occurring feature in each row.

To address the mismatches in Figure 4, we select

the most occurring feature in each row and keep this

feature only if it occurs more than two thirds of the

time (including the empty places). For row 2, we see

three times B and one time G. We can therefore con-

sider B as part of the complete match, and ignore G.

All rows in our example have a feature that is occur-

ring two thirds of the time, except for the third row.

Therefore, we will remove C (and F) from our multi-

camera feature set. Since C is only supported by two

cameras, it is too weak to be considered as a reliable

inlier, and is hence removed from the list.

By this method, we create a set of features for the

feature from C

, where we have calculated that they

all presumably belong together. We will add this set

of features to the global list of multicamera matches,

after checking for duplicates. This process is repeated

for every combination ofC

andC

, and for every fea-

ture pair between these cameras.

An example for three cameras is shown in Fig-

ure 6. Here, 318 matches were found over 3 cam-

eras. There were 2661, 3168, and 3011 matches in

the three images resulting in 1171, 951, and 1088

matching features between pairs of images. By using

the algorithm above, only 318 matches were retained,

therefore yielding a higher robustness.

5 ANGLE-BASED 2D IMAGE

CORRESPONDENCES

SELECTION

Once the multicamera matches are determined, we

perform an angle-based ﬁltering which further en-

hances the correctness of the ﬁnal result of the cali-

bration by eliminating possible mismatches. The ba-

sis of this approach lies on the observation that cor-

rectly matched features in adjacent images have sim-

ilar vertical displacement across images because our

cameras are not rotated around the optical axis. More

conﬁdence is given to features that are more vertically

“consistent” in adjacent images as large discrepancy

in features’ vertical position is a good indication of

mismatch.

To perform a ﬁltering based on this vertical dis-

placement, we place a pair of images next to each

other and connect all matches between these images.

Next, we determine the angles between the horizon-

tal and the lines connecting the features. Of these

angles, we erase the top and bottom 5% and calcu-

late the average of the remaining angle values. We

will now discard any match of which the angle differs

more than 3 degrees from the average. This param-

eter is determined empirically and can be adjusted if

required. This is an effective outlier removal method,

as demonstrated in Figure 7 and 8. Figure 7 shows

the matches that passed the angle test. There are

288 matches, compared to the previous 318 matches.

Most outliers are effectively removed, and no valid

multicamera matches are erroneously removed. Fig-

ure 8 shows the matches where the angle test failed.

All these matches are outliers, and are therefore re-

moved from the succeeding calibration process.

This process is only applicable if the cameras are

not too much rotated relative to each other, especially

around the optical axis. If that were the case, the as-

sumption that lines connecting matching features are

more or less parallel would not be correct. For the lin-

ear camera arrangement, all cameras are set up such

that they are upright relative to each other. For the

curved camera arrangement, only 3 cameras are con-

sidered at a time, so that this angle-based selection

remains effective.

6 CORRESPONDENCES TO

PROJECTION MATRICES

Once the 2D correspondences are extracted and ﬁl-

Self-calibrationofLargeScaleCameraNetworks

111

Figure 7: Multicamera feature matches, considered as inliers. Most outliers are removed using the angle-based ﬁltering. Only

a subset of the muticamera matches are shown.

Figure 8: Multicamera feature matches, considered as outliers. These matches were rejected using the angle-based ﬁltering

method. There are no false outliers in this example. Only a subset of the muticamera matches are shown.

tered, they are sent to the calibration toolbox of (Svo-

boda et al., 2005). RANSAC (Hartley and Zisserman,

2003, page 117) is then used to further remove re-

maining outliers, and the projection matrices P are de-

termined based on the correspondences using a bun-

dle adjustment approach (Triggs et al., 2000)(Hartley

and Zisserman, 2003, page 434).

Furthermore, radial distortion is determined

(Hartley and Zisserman, 2003, page 189) and re-

moved before the extraction of intrinsic and extrinsic

matrices.

7 RESULTS

We veriﬁed the correctness of the calibration method

by applying it to a real dataset of soccer games. We

recorded three different soccer games using a multi-

camera setup, as shown in Figure 9. Some recorded

images are shown in Figures 10 and 11. All cam-

eras recorded the soccer game as described in section

2, and all cameras were synchronized. We extracted

10 images from the video stream at a rate of 1 im-

age per minute. Using these sets of images, we apply

the calibration method described earlier and verify the

results, by simulating a plane sweep approach (Yang

et al., 2003) and validating the relation between the

depth hypothesis and the projection matrices P, de-

ﬁned in section 3.

In essence, an object in 3D space at a given

depth plane in the scene will be projected to all cam-

era views with their respective projection matrices P.

Conversely, all the object’s projected 2D images in the

different camera viewswill coincide with one location

in space, when performing the inverse projection P

−1

towards the 3D object’s depth plane. For instance,

in Figure 12(a) the inverse projection of the yellow

foreground player from the camera views towards his

depth plane will bring all his projections in perfect

overlap into a focused image, while all surrounding

players at a different depth plane will present ghost-

ing duplicates. A similar observation can be made for

the focused blue background player of Figure 12(b)

if the depth plane under test is put exactly at his 3D

position.

It’s worth noticing that the plane sweeping algo-

rithm (Yang et al., 2003) exactly relies on testing dif-

ferent depth planes and detecting the focused image

for estimating the object’s depth. Given this depth in-

formation, we can now validate the camera calibration

by estimating all the projection matrices P, and eval-

uate whether the inverse projections over all cameras

provide an object in focus at the given depth plane. If

not, at least one of the projection matrices would have

been incorrectly evaluated.

The results for our datasets are shown in Figure

12. We have chosen a few depth planes that coincide

with players in the scene. The above described proce-

dure brings the players at their corresponding depth

plane always in focus. This demonstrates the cor-

rectness of our method and the applicability in recon-

struction algorithms for soccer scenes (Goorts et al.,

2013; Goorts et al., 2014).

When using the multicamera matches without the

angle-based selection, no valid calibration is returned

by the calibration toolbox, clearly validating the use-

fulness of the approach.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

112

(a) (b)

Figure 9: The camera setup used to generate our datasets. (a) The linear setup. All cameras are placed on a line. (b) The

curved setup. The cameras cover a quarter circle.

(a) (b)

(e) (f)

Figure 10: Some frames from the input datasets. The cameras were placed in an arc setup at the top of the stadium. The

cameras were aimed at the penalty area.

Self-calibrationofLargeScaleCameraNetworks

113

(a) (b) (c)

(d) (e) (f)

(g) (h) (i)

(j) (k) (l)

Figure 11: Some frames from the input datasets. The cameras were placed in a linear setup at the top of the stadium. Two

focal lengths were used.

8 CONCLUSION

We presented a method to generate multicamera

feature correspondences for self-calibration in large

scale camera networks, using existing calibration

toolboxes. Pairwise feature matches are propagated

over all camera views using a conﬁdent-based voting

method. Features following a connecting line corre-

sponding to the apparent movement across adjacent

images are kept; all other features are considered as

outliers and discarded. The remaining multicamera

features can then reliably be used by existing calibra-

tion toolboxes,yielding correct camera calibration pa-

rameters. We demonstrated the quality of our method

using a multicamera projection-based approach. Fu-

ture effort will be directed to a more efﬁcient ap-

proach and a more general ﬁltering, i.e. allowing ro-

tation of the cameras over the optical axes.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

114

(a) (b)

(e) (f)

Figure 12: Visual results of reprojecting the calibrated images to a plane in the scene. If the same object in every image

projects to the same location on a single plane, then the camera calibration is correct. The images above show the projection

for some planes on different depths. The objects in the red boxes all project to the same location, demonstrating the correctness

of our method.

REFERENCES

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:

Speeded up robust features. In Computer Vision–

ECCV 2006, pages 404–417. Springer.

Doshi, A., Starck, J., and Hilton, A. (2010). An empirical

study of non-rigid surface feature matching of human

from 3d video. Journal of Virtual Reality and Broad-

casting, 7(10).

Farin, D., Han, J., and de With, P. H. (2005). Fast cam-

Self-calibrationofLargeScaleCameraNetworks

115

era calibration for the analysis of sport sequences. In

Multimedia and Expo, 2005. ICME 2005. IEEE Inter-

national Conference on, pages 4–pp. IEEE.

Farin, D., Krabbe, S., Effelsberg, W., et al. (2003). Robust

camera calibration for sport videos using court mod-

els. In Electronic Imaging 2004, pages 80–91. Inter-

national Society for Optics and Photonics.

Goorts, P., Ancuti, C., Dumont, M., and Bekaert, P. (2013).

Real-time video-based view interpolation of soccer

events using depth-selective plane sweeping. In Pro-

ceedings of the Eight International Conference on

Computer Vision Theory and Applications (VISAPP

2013). INSTICC.

Goorts, P., Maesen, S., Dumont, M., Rogmans, S., and

Bekaert, P. (2014). Free viewpoint video for soccer

using histogram-based validity maps in plane sweep-

ing. In Proceedings of the Ninth International Con-

ference on Computer Vision Theory and Applications

(VISAPP 2014). INSTICC.

Grau, O., Prior-Jones, M., and Thomas, G. (2005). 3d mod-

elling and rendering of studio and sport scenes for tv

applications. In Proceedings of WIAMIS.

Hartley, R. and Zisserman, A. (2003). Multiple view geom-

etry in computer vision, volume 2. Cambridge Univ

Press.

Hayet, J.-B., Piater, J. H., and Verly, J. G. (2005). Fast

2d model-to-image registration using vanishing points

for sports video analysis. In ICIP (3), pages 417–420.

Li, Q. and Luo, Y. (2004). Automatic camera calibration for

images of soccer match. In International Conference

on Computational Intelligence, pages 482–485.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International journal of computer

vision, 60(2):91–110.

Ohta, Y., Kitahara, I., Kameda, Y., Ishikawa, H., and

Koyama, T. (2007). Live 3D Video in Soccer Stadium.

International Journal of Computer Vision, 75(1):173–

187.

Svoboda, T., Martinec, D., and Pajdla, T. (2005). A conve-

nient multicamera self-calibration for virtual environ-

ments. Presence: Teleoperators & Virtual Environ-

ments, 14(4):407–422.

Thomas, G. (2007). Real-time camera tracking using sports

pitch markings. Journal of Real-Time Image Process-

ing, 2(2-3):117–132.

Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,

A. W. (2000). Bundle adjustmenta modern synthesis.

In Vision algorithms: theory and practice, pages 298–

372. Springer.

Yang, R., Welch, G., and Bishop, G. (2003). Real-time

consensus-based scene reconstruction using commod-

ity graphics hardware. Computer Graphics Forum,

22(2):207–216.

Yu, X., Jiang, N., Cheong, L.-F., Leong, H. W., and Yan,

X. (2009). Automatic camera calibration of broadcast

tennis video with applications to 3d virtual content in-

sertion and ball detection and tracking. Computer Vi-

sion and Image Understanding, 113(5):643–652.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 22(11):1330–1334.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

116