
Optimizing Elliptic Curve Scalar Multiplication
with Near-Factorization
Pratik Poddar, Achin Bansal and Bernard Menezes
Department of Computer Science, Indian Institute of Technology - Bombay , Mumbai 400076, India
Keywords: Elliptic Curve Cryptography, Scalar Multiplication, near-Factorization, NAF, Window NAF, Koblitz
Curves.
Abstract: Elliptic curve scalar multiplication ( P where is an integer and P is a point on the elliptic curve) is
widely used in encryption and signature generation. In this paper, we explore a factorization-based approach
called Near-Factorization that can be used in conjunction with existing optimization techniques such as
Window NAF (Non Adjacent Form). We present a performance model of Near-Factorization and validate
model results with those from a simulation. We compare Near-Factorization with wNAF for a range of
scalar sizes, window sizes, divisor lengths and Hamming weights of divisor. The use of Near-Factorization
with wNAF results in a considerable reduction in the effective Hamming weight of the scalar and a
reduction in overall computation cost for Koblitz curves.
1 INTRODUCTION
Elliptic Curve Cryptography (ECC) has received
much attention in recent years. For the same level of
security, its performance surpasses that of RSA and
other public key cryptographic schemes. All public
key cryptographic algorithms, however, are orders
of magnitude more compute-intensive compared to
their secret key counterparts and are the bottleneck
in widely used protocols such as SSL/TLS. Hence,
there is a dire need to optimize their performance.
The elliptic curve operation of scalar
multiplication is widely used in encryption,
decryption and signature generation/verification.
Denoted []P, where is an integer and P is a point
on the elliptic curve, it involves computing P + P +
. . . + P (times). Scalar multiplication is
implemented using point doublings and point
additions. Some of the best known methods of
reducing the number of additions are the use of the
NAF (Non Adjacent Form) (Morain, 1990) or
multi-base representation (Dimitrov, 2005) of the
scalar, . On the other hand, to reduce the
computation time of the point doublings, point
halving has been suggested as an alternative
(Knudsen, 1999), (Schroeppel, 2000). For the
special case of Koblitz curves (Koblitz, 1992),
(Solinas, 2000), the - adic operation replaces point
doubling and results in greatly reduced cost of scalar
multiplication. One of our goals is to investigate
whether the cost of cryptographic operations can be
reduced even further especially in the context of
Koblitz curves.
In this paper, we explore an optimization called
Near Factorization based on expressing the scalar
as where and are respectively the
quotient and remainder obtained by dividing by a
divisor, . This form of the scalar, , was earlier
studied in (Ciet, 2003) in a completely different
context that of resistance to side channel attacks
while our objective is to investigate the performance
implications of Near Factorization. is chosen to
have low Hamming weight (for example 3). For
each such , we compute the combined Hamming
weight of , and . We select the combination
with minimum Hamming weight to reduce the
number of point additions. Despite the considerably
reduced search space, the cost of this search will not
be insignificant. So, the application of Near
Factorization will likely be limited to scenarios
where P is unknown but the scalar may be chosen
beforehand as in Diffie-Hellman Key Agreement
(Diffie, 1976) or in encrypting a message
(Hankerson, 2004) using a public key just received
via a digital certificate.
We use Near Factorization in conjunction with
wNAF (window NAF). We develop an analytical
model to estimate the performance of NF+wNAF
and compare the model output with simulation
361
Poddar P., Bansal A. and Menezes B..
Optimizing Elliptic Curve Scalar Multiplication with Near-Factorization.
DOI: 10.5220/0005058703610370
In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 361-370
ISBN: 978-989-758-045-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

results. We experiment with a range of window
sizes, scalar lengths, divisor lengths and divisor
Hamming weights and identify the best combination
of these. Our main result is that NF+wNAF reduces
the number of point additions vis-à-vis wNAF by up
to 10% in the case of Koblitz curves.
Section 2 summarizes work related to this paper
while Section 3 contains a brief review of wNAF. In
Section 4, we introduce Near Factorization and
develop a model that captures the resulting reduction
in Hamming weight. Section 5 highlights practical
considerations and our main results. Section 6
contains a summary and our conclusions.
2 RELATED WORK
There are a myriad of proposed strategies for
minimizing the cost of scalar multiplication
(Gordon, 1998). If the entity computing kP has
the prerogative of crafting k, he may choose k with
low Hamming weight. This reduces security since it
results in a decrease in search space of k. For
example, (Coron, 2005), (Muir, 2006) present an
algorithm to efficiently solve the discrete logarithm
problem when the Hamming weight of k is known.
A tradeoff between security and performance is to
choose k as a product of low Hamming weight terms
k
, k
, . . . k
as in (Hoffstein, 2003). Here, the
cost of scalar multiplication is proportional to the
sum of the Hamming weights of the factors of k but
the total number of possible values for k is the
product of the number of possible values of each
factor.
The other option is to accept k from a “good”
random number generator and find alternate number
representations of k which minimize the Hamming
weight and the computation cost. NAF and wNAF
(Morain, 1990) are two such examples. The number
of point additions and doublings in scalar
multiplication was formalized through the notion of
an addition chain (Knuth, 1998). An addition chain
for k is a list of positive integers, k
= 1, k
=2, .
. . ,k
= k such that for each i 1, there is some
j and m, 1jmi, such that k
= k
k
.
(m j corresponds to point doubling while m j
corresponds to point addition in the context of scalar
multiplication). The optimal cost is obtained by
finding the shortest possible chain length, n.
Minimal chain lengths for small values of k are
readily available. However, for large values of k,
only upper and lower bounds have been derived
(Erdos , 1960). Also, point additions and doublings
are lumped together – this is clearly not appropriate
since, in the case of Koblitz curves, the cost of a τ-
adic operation (in lieu of doubling) is considerably
less than that of a point addition.
There have been a number of variations and
extensions to wNAF. Fractional wNAF, introduced
in (Moller, 2003), was motivated by considerations
of optimal memory utilization in resource-
constrained/embedded devices. It provides many
more options in the number of points that need to be
precomputed (rather than just2
1 ) – thus
the window size may be tailored to the available
storage. In addition, a left-to-right recoding scheme,
resulting in the MOF (Mutually Opposite Form)
representation of a scalar, was proposed in (Joye,
2000) for w = 2 and generalized for w > 2 in
(Okeya, 2004) to save memory. The non-zero
densities in fractional wNAF and fractional wMOF
were investigated in (Fan, 2005), (Schmidt, 2006). It
was shown that the Hamming weight in fractional
wNAF and wMOF was no better than in wNAF for
the same window size.
(Dimitrov, 2005) proposed a representation of
the scalar, k using mixed powers of 2 and 3. This
Double-Base representation is sparse and
consequently reduces the number of point additions
though it requires efficient algorithms for point
tripling. (Adikari, 2011) introduced an easily
computable hybrid binary-ternary number
representation for k (a special case of double base
chains). They studied its performance through a
Markov chain analysis as well as through software
implementation. (Dimitrov, 2007) added radix 5 thus
generalizing the two base representation to those
with three and more (multi-base representations).
Motivated by considerations of memory usage,
(Doche, 2006), (Barua, 2007) proposed a window-
based implementation. The work in this paper aims
to reduce the number of additions while leveraging
the extremely low cost of τ-adic operations in
Koblitz curves to reduce overall computation time.
The Near Factorization approach is closest in
spirit and indeed has been inspired by the “factor
method” suggested in (Knuth, 1998) wherein
working with the factors of k may yield a reduction
in cost. The scalar product, 55P , for example, may
be computed in two steps:
Q = 5P = 2 ( 2P ) + P and 55P = 11Q =
2 ( 2 ( 2Q ) ) + 2Q + Q
The factor approach involves a total of 8 adds
and doubling operations while the “binary method”
involves 9 operations. Near Factorization is a
SECRYPT2014-InternationalConferenceonSecurityandCryptography
362
generalization of the factor method which allows for
a non-zero remainder. As mentioned earlier, the
scalar, k, was represented as dqr in (Ciet, 2003),
where d is randomly selected. However, the main
goal of that work was to extend resistance to side-
channel attacks in ECC computations. There was no
attempt to reduce the combined Hamming weight of
d, q and r or to quantify the savings in computation
time resulting from a decrease in Hamming weight.
3 REVIEW OF WINDOW NAF
wNAF-based scalar multiplication involves two
steps – the wNAF representation of the scalar is first
computed followed by point doubling and point
addition on the wNAF representation.
The wNAF representation of a scalar, k is k =
∑
k
2
where k
∈{ 0 , 1 , …. , (2
- 3) ,
(2
- 1) }. l , the number of digits in the NAF
representation, is either |k| or |k| + 1 where |x| is the
number of bits in the binary representation of x . The
wNAF representation may be obtained by scanning
w-bit overlapping windows of the binary
representation of k from right to left. An important
feature of the wNAF representation of a scalar is
that there are at least w1 zeros separating two
non-zeros.
Example 1: The binary, 2NAF and 4NAF
representations of the scalar k = 796404706727234
are respectively
101101010001010011011010111010010001010101
01000010,
101
01
010100010101001
001
01
001
0100100010101
0101000010 and
10005
00050000050000700005
0001
0007
000100050
005000010
Here, x denotes a weight of -x. The Hamming
weight of the 4NAF representation is 12 compared
with 20 in the 2NAF representation and 23 in the
simple binary representation.
Scalar multiplication with an -bit scalar in
simple binary involves 1 point doublings and
⁄21 point additions on average. The expected
number of non-zeros in the wNAF representation of
an -digit scalar is roughly ⁄1 . With
wNAF, w > 2, the points 3P , 5P, . . . (2
– 1)P
and their negatives are first computed. So, this pre-
computation cost (ignoring unary negation) is that of
only 1 point doubling and 2
1 point additions
yielding total mean computation cost = D +
2
2
A where D and A are
respectively the times to compute a point doubling
and a point addition.
Table 1: Acronyms and Notation.
wNAF()
NAF representation of an
integer, with window size =
,
1
Probability that a wNAF string of
length has Hamming weight
1
NF+wNAF
Near Factorization on a wNAF
represented scalar
,
1
# of wNAF strings of length
with Hamming weight 1
P, Q Points on an Elliptic Curve
Total # of wNAF strings of length
,
is the length of scalar,
′,
Prob ( | across all
iterations)
, ,
Quotient and remainder
obtained by dividing by
divisor,
,
Prob ( | given that
digits of | are random )
′,′′
Shifted quotients
,
Probability that
|
||
Length of string,
′,
Prob( | across all
iterations)
|
Concatenation of strings and
Total # of possible values of
Hamming weight of string (#
of non-zeros in )
Total # of values of with random
digits
OptimizingEllipticCurveScalarMultiplicationwithNear-Factorization
363

4 NEAR-FACTORIZATION
4.1 Description of NF+Wnaf
With Near Factorization, the scalar,, is
represented as and are the
remainder and quotient obtained from dividing by
the divisor, ). []P is computed as follows
Step 1: Compute Q = []P
Step 2: Compute
[]P = []Q + []P
Instead of computing []Q and []P separately,
their computations are interleaved using Shamir’s
Ladder as below.
Input: Scalars , and
elliptic curve points Q , P
Output: R = []Q + []P
Let
|
|
…
and
|
|
…
denote the wNAF representations of
and .
R = O
for 0 to || 1 {
R ← [2]R
R ← R +
|
|
Q +
|
|
P
}
The cost of Step 1 is
|
|
1 point doublings
and
1 point additions while that of Step 2 is
|
|
1 point doublings and
1
point additions. The combined cost is
|
|
|
|
2
D
2
(1)
For 160-bit and an 80-bit divisor, an
exhaustive search of divisor space to minimize
Equation 1 is infeasible. Instead, we find a local
minimum of the computation cost (Equation 1) by
iterating over all possible values of with a positive
digit in the most significant position and low
Hamming weight (3 or less, for example). We refer
to this step as Step 0.
Example 2: Near Factorization on the scalar =
796404706727234 (in Example 1) with 2NAF
representations yields
= 1010000000000000000001
000
= 10010001001
0001
01
00000001
0
= 1000000000001010101
0010
The Hamming weights of , and are
respectively 3, 7 and 6 resulting in 14 point
additions. The corresponding number of additions
using NAF sans Near Factorization is 19. Thus,
NF+2NAF involves 26% fewer point additions. The
number of point doublings are 50 and 49 with 2NAF
and NF+2NAF respectively.
With NF+4NAF , and are
= 70000000500000000007
00000
= 300007000300000000003
0
= 3000005000000000010
The number of point additions with NF+4NAF is
8 versus 11 with 4NAF.
We next model the combined Hamming weight
of quotient and remainder obtained through Near
Factorization.
4.2 Modeling Cost of NF
The first step in our model is to compute ,
1 – the probability that an arbitrarily selected
and valid NAF string of digits has
Hamming weight 1. A valid NAF string
satisfies the following:
(i) The digits in the string are
drawn from the set
S = { - (2
- 1) , - (2
- 3) , …. , -1 , 0 , 1 , …. ,
(2
- 3) , (2
- 1) }
(ii) Any two non-zeros in the string
are separated by at least 1
zeros.
(iii) The string begins with a
positive integer from the above
set S
Let denote the number of NAF
strings of length starting with a 1. Since it is
equally likely that a NAF string begins with a 1 or
3or . . . , 2
1, the total population of
NAF strings of length is 2
. Also, let , 1 denote the number
of NAF strings of length and Hamming
weight 1.
So,
, 1
,
(2)
To compute ,1 , we note that the
leftmost non-zero in each NAF string accounted
for in the numerator can take 2
possible values
while each of the remaining non-zeros may take
SECRYPT2014-InternationalConferenceonSecurityandCryptography
364

one of 2
possible values. Further, each non-
zero digit, except for the rightmost, must be
followed by at least 1 zeros. The number of
ways the remaining
1
– 1
zeros may be placed in 1 possible bins
(corresponding to the 1 bins of zeros to the
right of each non-zero digit) is
1
w1
(This problem is analogous to counting the
number of non-negative integral solutions to the
equation
...
which is
1
1
). Here, 1
1 and 1.
So,
,1
2
2
1
w1
(3)
Substituting into Eq. 2
,1
2
1 w 1
(4)
To obtain a closed-form expression for
, we note that the first non-zero after the leftmost
digit of a wNAF string may take one of 2
possible values and be separated from the leftmost
digit by at least 1 zeros. So, can be
expressed recursively as
2
2
1
2
2 ......2
1
(5)
Expressing as a
th
order recurrence,
12
(6)
The characteristic equation of this recurrence is
–
2
0
Let r
1
, r
2
, …. , r
w
be the roots of the above
equation (these are unique at least up to =6). So,
….
(7)
From the initial conditions, 1 = 1, 2 = 1,
….., = 1, the coefficients,
, and hence
may be computed and used in Equation
4.
Let be the number of different divisors over
which the Near Factorization Algorithm iterates.
While the values of the quotients and remainders are
not unique across iterations, the concatenated
quotient and remainder, |, is. As explained below,
the values of | are not necessarily independent
across iterations.
Figure 1 illustrates the relationship between the
dividend, quotient and remainder (the dividend is the
original scalar, ). Three shifted quotients are shown
– the extent of their shifts is dictated by the positions
of the three non-zeros in the divisor, , as depicted
in the figure. The sum of the shifted quotients
(denoted , ’ and ’’) and remainder equals the
dividend. The Near Factorization Algorithm iterates
over all possible positions of the non-zeros in the
divisor. During each iteration, ’ and ’’ are
positioned differently. This, in turn, affects different
bits of the quotient and remainder and in seemingly
random ways.
Figure 1: Illustrating random and fixed digits in |.
Imagine projecting the positions of ’ and ’’ on
to the quotient and remainder as shown in Figure 1.
To a first order approximation, the remaining bits in
the quotient and remainder “inherit” directly from
the given scalar or dividend. Because the latter is a
given, these bits do not contribute to a possible
decrease in Hamming weight of quotient and
remainder. On the other hand, the bits of the
remainder and quotient which lie “directly under” ’
and ’’ are random and so potentially contribute to a
decrease in the Hamming weights of the quotient
and/or remainder across iterations.
Let denote the maximum length of | across
iterations. Of these, let denote the total number of
bits that appear directly under ’ or ’’. These bits
are random and the remaining are ‘fixed’.
From the property of the wNAF representation, the
OptimizingEllipticCurveScalarMultiplicationwithNear-Factorization
365
Hamming weight of the fixed bits is /
1 on average. Let
,
denote the conditional
probability that the -bit quotient + remainder in an
iteration of Near Factorization has Hamming weight
given that bits of the quotient + remainder are
random.
So,
,
,
,
0
(8)
Let
,
be the probability that an -bit
quotient + remainder has Hamming Weight . Of
the different values of divisor, , let
be the
number of values for which the quotient + remainder
has random bits. So,
,
,
(9)
There are three possibilities for . If the
Hamming weight of the divisor is 2, then ||.
If the Hamming weight of the divisor is 3, there are
two possibilities – either the positions of ’ and ’’
overlap or they don’t. In the former case,
2|| where is the number of positions in
which ’ and ’’ overlap. In the latter (non-
overlapping) case, 2||. Enumerating the
number of ways each case may occur, we get
||
2
|
|
(10)
|
|
2
|
|
|
|
1
|
|
(11)
|
|
2
||
|
|
|
|
if
|
|
|
|
0otherwise (12)
Let ′
,
denote the probability that the sum
of the Hamming weights of the quotient and
remainder across all iterations is greater than . So,
′
,
, 1
, 2
⋯,
(13)
The probability that this sum is precisely is
′
, 1–
′
,. Hence, the expectation of
the minimum Hamming weight is
′
,1
′
,
(14)
To test the accuracy of the above model, we
performed Near Factorization on 5000 randomly
generated 200-bit scalars. For each integer, we
experimented with divisor size, || ranging from 20
to 180 bits in steps of 20 bits and also for = 2, 3, 4
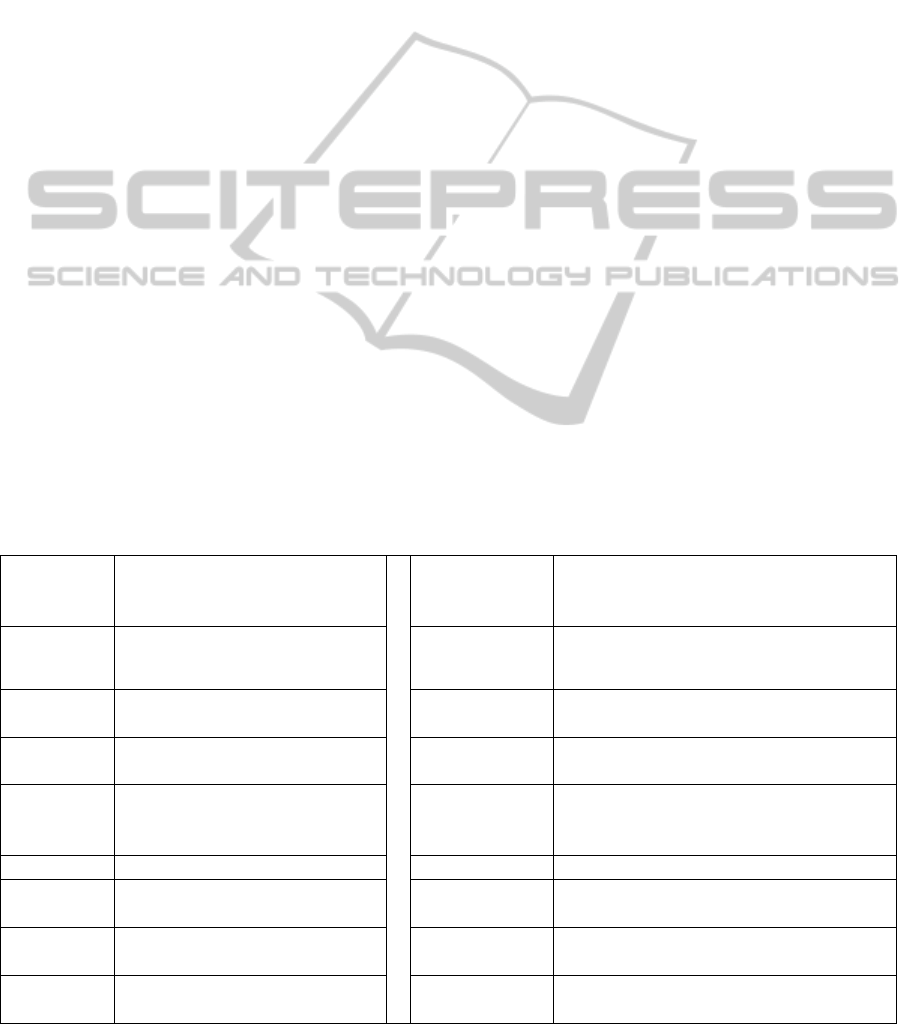
and 5. Figure 2 shows the Hamming weight of |
using Near Factorization averaged over the 5000
scalars. The figure juxtaposes the experimental and
model results. There is a close match between model
and experimental results for values of || up to
around 140. An important observation is that the
graphs obtained decrease monotonically up to
around 60 bits followed by a trough between ||= 60
and 120 followed by a sharp increase beyond
||=140.
Figure 2: Hamming Weight of q|r versus |d| - Model and
Exp. Results (|k| = 200).
5 RESULTS
5.1 NF+wNAF versus wNAF
Hamming Weight Comparison
To illustrate the advantage of Near Factorization, we
generated 200 random 200-bit scalars and computed
the Hamming weight of (a) q|r for each scalar
using its NF+wNAF representation with |d| = 100
(b) its simple binary representation.
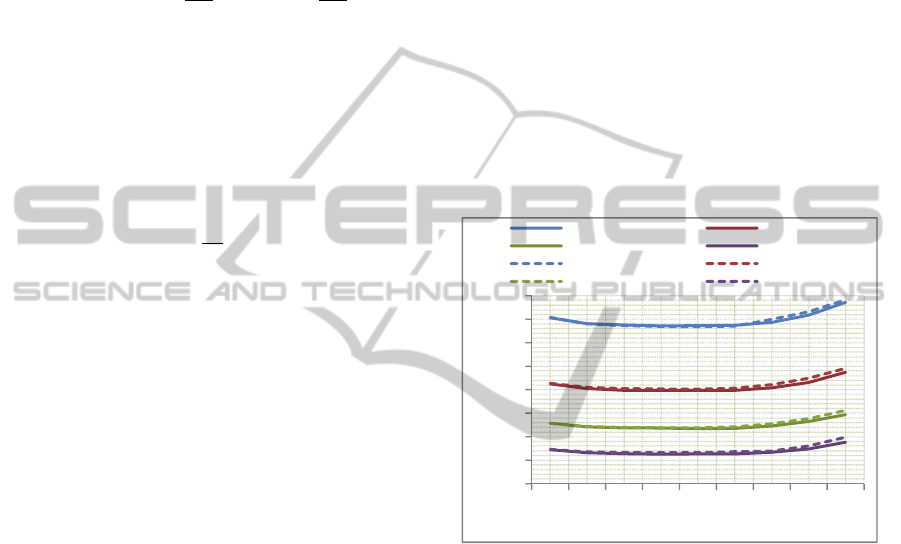
Figure 3 shows these values for = 2. For ease
of viewing, we arranged the scalars in increasing
order of the Hamming weights in their binary
representations and, within this ordering, in
increasing order of the Hamming weights in their
NAF representations. The average Hamming
20
25
30
35
40
45
50
55
60
20 40 60 80 100 120 140 160 180
HW(q|r)
|d|
Exp(w=2) Exp(w=3)
Exp(w=4) Exp(w=5)
New(w=2) New(w=3)
New(w=4) New(w=5)
SECRYPT2014-InternationalConferenceonSecurityandCryptography
366
weights for NF+wNAF and wNAF are respectively
53.3 and 67.
Figure 3: Hamming Weight – Binary versus NAF versus
NF+2NAF (|k| = 200, w = 2).
Figure 4: Hamming weight of Quotient + Remainder vs |k|
for NAF and NF+wNAF.
Figure 4 shows how the average Hamming
weight scales up with scalar size, |k|, in wNAF and
NF+wNAF for different window sizes. In each
case, the average Hamming weight and the decrease
in Hamming weight of NF+wNAF over wNAF
appears to be linear in the size of the scalar. It is well
established in the literature that the slope with
wNAF is 1/(+1). With NF+wNAF, the slopes are
.29 for w=2 (versus .33 for NAF), .22 for w=3
(versus .25 for NAF), .18 for w=4 (versus .2 for
NAF) and .15 for w=5 (versus .17 for NAF).
5.2 NF+wNAF versus NAF -
Comparison of Total Cost
In addition to the Hamming weight, the other major
contributors to cost are the point doublings and
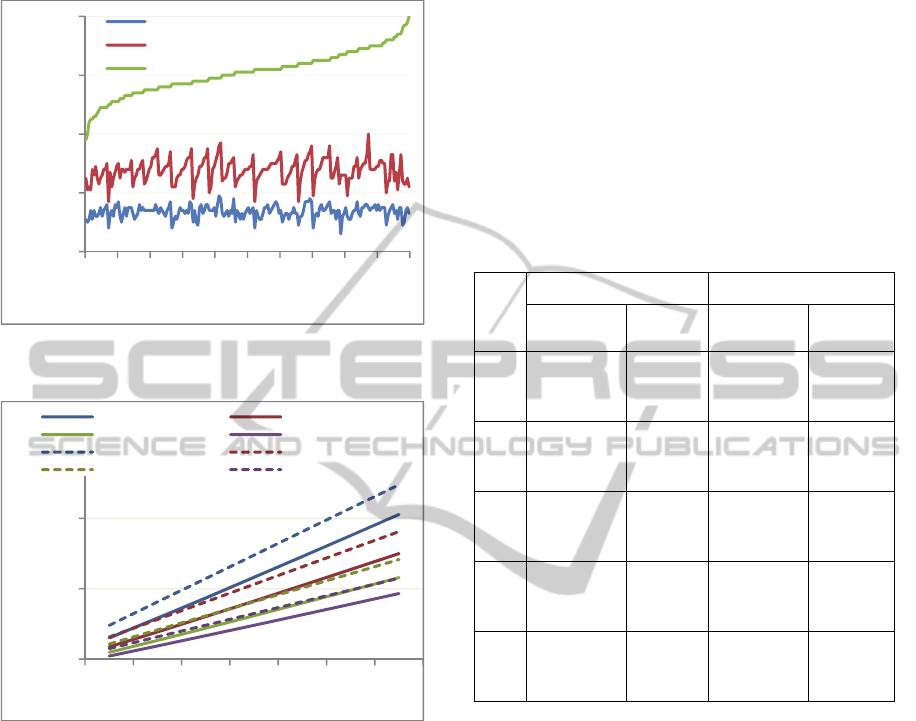
precomputation (for 2). Table 2 highlights
these for || = 200, || = 100. For both wNAF and
NF+wNAF, the number of point doublings is
|
|
1, independent of window size. For 2,
the precomputation cost (in Step 1) is an extra
doubling plus 2
– 1 point additions (shown to the
right of the plus sign under the “Avg # Additions”
columns of Table 2). These precomputations can be
reused in computing []P in Step 2. The need for
precomputations to obtain []Q is obviated by a
deliberate choice of = 2 in the representation of .
Table 2: Total Computation Cost ( |k| = 200 ) A = Cost of
Point Addition, D = Cost of Point Doubling.
WS
NAF NF+wNAF
Avg. #
Additions
Total
Cost
Avg. #
Additions
Total
Cost
2 65.6 + 0 65.6A
+
199D
54.4 + 0 54.4A+
199D
3 49 + 1 50A +
200D
42.1 + 1 43.1A
+
200D
4 39 + 3 42A +
200D
34.5 + 3 37.5A
+
200D
5 32.3 + 7 39.3A
+
200D
29.4 + 7 36.4A
+
200D
6 27.6 + 15 42.6A
+
200D
25.6 + 15 40.6A
+ 200D
From Table 2, it is clear that NF+wNAF
outperforms wNAF across all window sizes. In both
cases, the total number of point additions decreases
monotonically from =2 until =5 and then
increases because precomputation cost grows
exponentially with .
The work in this paper is particularly relevant to
Koblitz curves. These are elliptic curves defined
over F
2
but the co-ordinates of points on the curve
are elements of the binary field, F2
. Koblitz
curves are attractive in cryptography since the point
doubling operations can be substituted by the
inexpensive τ-adic operations. The τ-adic operation
on a point, ≡
,
returns the point with
coordinates
,
, i.e.,
,
,
and
∞
∞.
It is possible to represent each element in F(2
)
as a linear combination of elements in a normal
basis [28], ,
2
, . . .
. Each field
element is represented as an -bit vector and
40
60
80
100
120
1
21
41
61
81
101
121
141
161
181
HW(q|r) or HW(k)
Scalar Number
NF+wNAF(w=2)
wNAF(w=2)
Binary
10
60
110
100 150 200 250 300 350 400
Hamming Weight
|k|
NF+wNAF(w=2) NF+wNAF(w=3)
NF+wNAF(w=4) NF+wNAF(w=5)
wNAF(w=2) wNAF(w=3)
wNAF(w=4) wNAF(w=5)
OptimizingEllipticCurveScalarMultiplicationwithNear-Factorization
367

squaring is simply a left shift. Thus the τ-adic
operation has insignificant computation cost vis-à-
vis point addition. The ratio of elliptic curve point
addition to field squaring is likely to vary between
one and two orders of magnitude depending on
optimizations employed in the operations,
underlying platform (processor and operating
system) and compiler used. Above all, it will
depend on whether scalar multiplication is
implemented in hardware or in software. Analogous
to the wNAF representation, we use a –adic NAF
or TNAF representation for Koblitz curves. The
properties of TNAF are similar to the NAF
representation with average Hamming Weight = /3.
The algorithm to derive the TNAF representation
and perform scalar multiplication using TNAF are
described in (Solinas, 2000), (Hankerson, 2004).
Our final experiment was to vary all three
parameters – window size, divisor length and
Hamming weight of divisor. For ||=200, we
experimented with || ranging from 10% to 50% of
||in steps of 10%. As before, we fixed=2 for the
divisor but varied between 2 and 5 for the
quotient + remainder. We also experimented with
different Hamming weights for the divisor between
3 and 5. Table 3 lists the total number of additions
including pre-computations for the most attractive
combination of the above parameters.
From Table 3, the fewest number of point
additions with a 200-bit scalar occurs for = 5, ||
= 100 and maximum Hamming weight of divisor =
4. This represents an improvement of about 10% for
NF+wNAF over wNAF – 35.6 versus 39.3 additions
(see Table 2, = 5). The price to be paid for this
improvement is the large search space of divisors to
be processed in Step 0 – the numbers in parentheses
within each cell of Table 3 specify the number of
divisions to be performed which, in this case,
exceeds 1 million. On the other hand, decreasing the
length of divisor greatly reduces the cost of Step 0 at
the expense of a modest increase in the average cost
of the additions vis-a-vis || = 0.5|| (the optimal
choice from Figure 2). For example, with Hamming
weight = 3 and = 5, the improvements of
NF+wNAF over wNAF are 6.6% and 5.3%
respectively for || = 0.4|| and || = 0.2||. The
corresponding number of divisions in Step 0 shows a
drastic fall to 2740 and 580 respectively.
Even restricting the Hamming weight of divisor
to 3, the overhead of Step 0 is substantial –
,
where is the length of the scalar. Clearly, this
approach is only appropriate where the point P is
unknown but where the scalar, is known or may be
chosen beforehand as in Diffie-Hellman Key
Exchange (Diffie, 1976) where both parties derive
their common secret by performing a scalar
multiplication.
Table 3: Total Cost of Additions, |k|=200 DL = Divisor
Length.
DL
HW= 3 HW= 4
w = 4 w = 5 w = 4 w = 5
20
38.6
(580)
37.2
(580)
38.2
(5060)
37.1
(5060)
40
37.9
(2740)
36.7
(2740)
37.2
(59860)
36.3
(59860)
70
37.6
(8980)
36.4
(8980)
36.6
(375060)
35.8
(375060)
100
37.5
(18820)
36.4
(18820)
36.3
(1161860)
35.6
(1161860)
In response to receiving a partial key, P
A
from
A, B computes [
P
A
. Here, the scalar
, is a
random number chosen by B. But there is no reason
why
could not have been generated by B well
before session establishment. So long as
is
random, is not re-used and is stored safely in “near-
factorized form”, there is no drawback from the
perspective of security. Besides D-H key exchange,
the “unknown point, known scalar” situation occurs
in various encryption schemes.
Recently, (Taverne, 2011) have implemented
scalar multiplication in software while leveraging
the carry-less multiplier on newer Intel processors
for binary field multiplications. This results in a
dramatic improvement in performance to the extent
that the best implementation of scalar multiplication
on binary fields is about 17% faster than the best
implementation over prime fields. Moreover, scalar
multiplication with NIST Koblitz curves K-233 and
K-409 is about twice as fast as that over the
corresponding NIST random curves B-233 and B-
409. Near Factorization further improves on the best
albeit by a modest amount.
6 SUMMARY AND
CONCLUSIONS
This paper has explored an approach called Near
Factorization (a variation of the factor-based method
(Knuth, 1998)) to optimize scalar multiplication in
elliptic curves. The scalar , is divided by all
possible divisors of very low Hamming weight. The
divisor ’, quotient, ’ and remainder, ’ which
results in the lowest combined Hamming weight is
selected to obtain the “near factorized” form of ,
SECRYPT2014-InternationalConferenceonSecurityandCryptography
368

viz. ’ ’’. This form is employed in
two simple steps of NF-based scalar multiplication.
NF is used in conjunction with wNAF to further
improve performance. We constructed a model to
estimate the Hamming weight of |. Results of this
model closely match actual experimental results
across different scalar sizes, divisor lengths and
window sizes.
NF+wNAF reduces the number of point
additions over wNAF with no increase in point
doublings. In Koblitz curves, point doublings are
replaced by the inexpensive τ-adic operation. Hence,
the decrease in Hamming weight amplifies the
percentage improvement in overall computation time
of NF+wNAF over wNAF. For scalar length=200,
for example, NF+wNAF does 5-10% better than
wNAF – the actual improvement being a function of
the acceptable amount of Step 0 computation.
Other avenues for further exploration include the
use of Near Factorization twice to further reduce
cost. Another is a more efficient and effective search
of the space of divisors through intelligent pruning
to speed up Step 0.
REFERENCES
Erdos, P., 1960. “Remarks on number theory - On
addition chains,” Acta Arith., pp. 77–81.
Diffie, W., Hellman, M. 1976. “New Directions in
Cryptography”. In IEEE Trans. Information Theory,
vol. IT-22, no. 6, pp. 644-654.
Mullin, R., Onyszchuk, I., Vanstone, S., 1988. “Optimal
normal bases in GF(pn),” Discrete Applied
Mathematics, vol. 22, pp. 149-161.
Morain, F. Olivos, J. 1990. “Speeding up the
Computations on an Elliptic Curve Using Addition-
Subtraction Chains”. RAIRO Theoretical Informatics
and Applications, vol. 24, pp. 531-543.
Koblitz, N. 1992. “CM-curves with good cryptographic
properties”. In CRYPTO ’91, Advances in
Cryptology— (LNCS 576) [135], pp. 279–287.
Knuth, D., 1998."The Art of Computer Programming",
Semi numerical Algorithm, Vol. 2, 3rd Edn.,
Addison-Wesley, Reading, MA.
Gordon, D., 1998. “A survey of fast exponentiation
methods” . Algorithms,vol 27, pp. 129–146.
Cohen, H., Miyaji, A., Ono, T., 1998. “Efficient Elliptic
Curve Exponentiation Using Mixed Coordinates”. In
ASIACRYPT ’98, Proc. Int’l Conf. Theory and
Applications of Cryptology and Information Security
,pp. 51-65.
Knudsen, E., 1999. “Elliptic scalar multiplication using
point halving”. In ASIACRYPT ’99, Advances in
Cryptology— (LNCS 1716) [274], pp.135–149.
Lopez, J., Dahab, R., 1999. “Improved algorithms for
elliptic curve arithmetic in GF(2
n
)
”
. In SAC ’98,
Selected Areas in Cryptography (LNCS 1556) [457],
pp. 201–212.
Joye, M. Yen, S., 2000. “Optimal Left-to-Right Binary
Signed-Digit Recoding,” IEEE Trans. Computers, vol.
49, No. 7, pp. 740-748.
Schroeppel, R., 2000. “Elliptic Curve Point Halving Wins
Big”. Second Midwest Arithmetical Geometry in
Cryptography Workshop.
Solinas, J. , 2000. “Efficient arithmetic on Koblitz
curves”. Designs, Codes and Cryptography, 19: pp.
195–249.
Ciet, M., and Joye, M., 2003. "(Virtually) Free
Randomization Techniques for Elliptic Curve
Cryptography". In ICICS 2003, LNCS 2836, pp. 348-
359, Springer-Verlag.
Moller, B., 2003. “Improved Techniques for Fast
Exponentiation”. In ICISC 2003, LNCS 2587,
pp.298-312.
Hoffstein, J. Silverman, J., 2003. “Random small
Hamming weight products with applications to
cryptography”. Discrete Applied Mathematics 130(1):
pp. 37-49.
Hankerson, D., Menezes, A., Vanstone, S., 2004. "Guide
to Elliptic Curve Cryptography". Springer.
Moller, B. 2004. “Fractional Windows Revisited:
Improved Signed-Digit Representations for Efficient
Exponentiation”. In ICISC 2004, Proc. Int’l Conf.
Information Security and Cryptology , C. Park and S.
Chee, Eds., pp. 137-153.
Okeya, K., Schmidt-Samoa, K., Spahn, C., Takagi, T.,
2004. “Signed Binary Representations Revisited”. In
CRYPTO 2004, Proc., M.K. Franklin, ed., pp. 123-
139.
Coron, J., Lefranc, D., Poupard, G., 2005. “A New Baby-
Step Giant-Step Algorithm and some Applications to
Cryptanalysis”. In CHES 2005: pp. 47-60.
Fan, R., 2005. “On the efficiency analysis of wNAF and
wMOF”. Ph.D. Thesis, Technische Universitat
Darmstadt.
Dimitrov, V., Imbert, L., Mishra, P., 2005. “Efficient and
Secure Elliptic Curve Point Multiplication using
Double-Base Chains”. In Advances in Cryptology –
Asiacrypt 2005, LNCS Vol. 3788, pp. 59–78,
Springer,.
Doche, C., Icart, T., Kohel, D., 2006. “Efficient Scalar
Multiplication by Isogeny Decompositions”. Proc.
Conf. Public Key Cryptography, pp. 191-206.
Muir, J. Stinson, D., 2006. “On the low Hamming weight
discrete logarithm problem for non-adjacent
representations”. Appl. Algebra Eng. Commun.
Comput. 16(6): pp. 461-472.
Schmidt-Samoa, K., Semay, O.,Takagi, T., 2006.
“Analysis of Fractional Window Recoding Methods
and Their Application to Elliptic Curve
Cryptosystems”. In IEEE Transactions on Computers,
Vol.55, No.1, pp.48-57.
Doche, C., Imbert, L., 2006. “Extended Double-Base
Number System with Applications to Elliptic Curve
Cryptography”. In INDOCRYPT ’06, Proc. Conf.
Progress in Cryptology pp. 335-348.
OptimizingEllipticCurveScalarMultiplicationwithNear-Factorization
369

Dimitrov, V., Mishra, P., 2007. “Efficient Quintuple
Formulas for Elliptic Curves and Efficient Scalar
Multiplication using Multi base Number
Representation”. In ISC 2007, LNCS, vol. 4779, pp.
390-406. Springer, Heidelberg.
Barua, R., Pandey, S., Pankaj, R., 2007. “Efficient
Window-Based Scalar Multiplication on Elliptic
Curves using Double Base Number System”. In
Progress in Cryptology - Indocrypt 2007, LNCS Vol.
4859, pp. 351-360, Springer.
Taverne, J., Faz-Hernández, A., Aranha, D., Rodríguez-
Henríquez, F., Hankerson, D., López, J., 2011.
"Software implementation of binary elliptic curves:
impact of the carry-less multiplier on scalar
multiplication". In IACR Cryptology.
Adikari, J., Dimitrov, V., Imbert, L., 2011. “Hybrid
Binary-Ternary Number System for Elliptic Curve
Cryptosystems” . In IEEE Trans. Computers 60(2), pp.
254-265.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
370
