
Navigation of an Autonomous Mobile Robot Using Data Association
Method
Amir Monjazeb
1
, Jurek Z. Sasiadek
1
and Dan Necsulescu
2
1
Department of Mechanical and Aerospace Engineering, Carleton University, 1125 Colonel By Drive, Ottawa, Canada
2
Department of Mechanical Engineering, Ottawa University, 161 Louis Pasteur, CBY A205, Ottawa, Canada
Keywords: Simultaneous Localization and Mapping (SLAM) Problem, Unscented HybridSLAM, Unscented Kalman
Filter, Process Time, Root Mean Square (RMS) Position Error, Orientation Error.
Abstract: This paper presents an investigation on the performance of Unscented HybridSLAM using two different
mapping strategies. The global map estimation using Unscented Kalman Filter is scrutinized for different
scenarios, with and without the influence of a data association process. The accuracy of generated global
map under different vehicle speed settings and with different process time is demonstrated using computer
simulation. Results are discussed in terms of Root Mean Square (RMS) position error, orientation error, and
time of navigation process. Results show that depending on the application, and on a desired speed, a
compromise has to be done to get the best efficacy.
1 INTRODUCTION
Simultaneous Localization and Mapping (SLAM)
problem is often implemented in autonomous mobile
robots applications. SLAM is a situation in which a
mobile robot steers in an unknown environment and
constructs an instantaneous map and uses that map
to localize. Once localized, the robot updates the
map from its new location and this process occurs
simultaneously and in consequent fragments of time
(Durrant-Whyte, Bailey, 2006). SLAM was
introduced about three decades ago in terms of
uncertainty estimation of an erroneous dynamic
Bayesian network (Smith, Cheesman, 1986). Since
then, a continuous development of SLAM structure
and different solutions to the problem were
accomplished. Nowadays, SLAM is presented in
two major categories; feature-based and location-
based (Jaulin, 2011). This study focuses on some
aspects of the feature-based SLAM which furthers
the research on a new approach called Unscented
HybridSLAM (UHS) (Monjazeb et al., 2013). The
approach is combined of Unscented Kalman filter
(Julier, Uhlmann, 2001) and FastSLAM
(Montemerlo, et al., 2002) which is using the similar
navigational strategies in HybridSLAM (HS)
structure (Brooks, Bailey, 2009) and constrained
local sub-map filter (CLSF) technique (Williams, et
al., 2002). More specifically, this paper analyses the
UHS performance improvement using different
Scheduling of the application on CLSF. Some
aspects of sensor fusion were considered as well
(Sasiadek, 2002).
2 CONSTRAINED LOCAL
SUB-MAP FILTER
Constrained Local Sub-Map Filter (CLSF) is a
technique to fuse a local map to a global map. A
local map can be estimated using FastSLAM into the
whole picture of features in the environment
previously estimated by UKF. This technique
updates the full covariance matrix of the system
generated by UKF to be scheduled at “appropriate
intervals” (Williams, et al., 2002) defined by
FastSLAM based on Rao-Blackwellised Particle
Filter (RBPF) (Doucet, et al., 2000). This method
provides an independent, local sub-map estimate of
the point features in the environment in a small scale
and compares the local map that is statistically
sampled by particles (Bailey et al., 2006) with the
global map produced by UKF-SLAM algorithm.
Previous use of such method resulted in a map with
the reduction of uncertainty in EKF-SLAM (Brooks,
Bailey, 2009). Instead of using EKF to estimate
304
Monjazeb A., Z. Sasiadek J. and Necsulescu D..
Navigation of an Autonomous Mobile Robot Using Data Association Method.
DOI: 10.5220/0005059403040311
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 304-311
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

global and local maps separately and reducing
uncertainty, this approach may be substituted by a
combination of RBPF and UKF. The observations
are fused to create a local map by FastSLAM
referenced to a local frame of reference where its
global position is already estimated by UKF (Julier,
Uhlmann, 2004). At appropriate intervals, the
information contained in the local map is transferred
into the global map using formulated constraints
between the point landmark estimates. The
constraint would produce a map of the environment
and an estimated path that are identical to the ones
previously estimated by UKF. When the vehicle is at
location x
R
k
at time step k, a new frame of reference
is initiated (Negenborn, 2003). At this moment, the
path up to and including time step k is already
estimated in the same frame of reference with
respect to the global frame of reference and with its
minimum uncertainty (assuming it is zero). At the
same time step, the global local frame is initialized
under UKF calculation. However, the estimation in
the local frame of reference by RBPF is completely
independent of the estimation that is already done by
UKF in the Global frame of reference (Monjazeb et
al., 2012). At this time step, only a small state
covariance matrix of the system in the global frame
of reference is updated with the new observation.
Prior to the beginning of time step k+1, the key is
switched off to produce a fused map with minimum
uncertainty in the system. Once again, at the
beginning of time step k+1, the switch turns on to
send a local map and to fuse it into the global map
estimated by UKF to initiate the process of
generating a new global map (Monjazeb et al.,
2011).
3 SCHEDULINGS TECHNIQUES
The Unscented HybridSLAM algorithm is arranged
in such way so that UKF-SLAM estimates the whole
map of the environment and the RBPF estimates the
path and the local map in the vicinity of the current
robot position (Lijun, et al., 2011). At the CLSF
part, there will be an update only on features that are
observed in the current local frame of reference
(Lindemann, et al., 2006), and the remaining map
information will be untouched (Norgard et al.,
2000). When the information in the local map is
fused into the global map (Sasiadek, Hartana, 2000),
the resulting map is replaced with the map in the
previous time step. There are two distinct state
estimates independent from each other (Neira,
Tardos, 2001), and as a result, the augmented form
of posterior state in the process of map fusion can be
expressed as
k
x
ˆ
(CLSF)
={
G
k
x
ˆ
(robot)
,
G
m,
L
k
x
ˆ
(robot),
L
m}
(1)
where,
G
k
x
ˆ
(robot)
is the global posterior position of
the robot estimated by UKF,
L
k
x
ˆ
(robot)
is the local
posterior position of the robot estimated by RBPF,
G
m is the map of landmarks estimated by UKF and
L
m is the map of landmarks in the vicinity of the
robot’s pose only and estimated by RBPF. The
system covariance is defined as
k
P =
k
L
k
P
P
0
0
G
(2)
k
P
G
=
kmmkmL
kmLkLL
PP
PP
GG
GG
(3)
k
L
P =
k
L
mmk
L
mR
k
L
Rmk
L
RR
PP
PP
(4)
k
L
RR
P
is the robot covariance in the local frame of
reference,
k
L
mm
P
indicates covariance in the local
frame of reference related to landmarks,
k
L
Rm
P
and
k
L
mR
P
represent covariance on robots and landmarks
in the local frame of reference as well.
kmL
P
G
,
kmL
P
G
,
and
kmm
P
G
represent same covariance matrices as
above but in the global frame of reference. Finally,
kLL
P
G
is the covariance of the estimate of the local
frame of reference with respect to the global frame
of reference. In this approach, the position of the
robot and the map in the vicinity of the robot
position is estimated using particle filters. The
resulted data is converted to a single Gaussian and
by the use of CLSF the estimated local map is fused
to the Global map previously estimated by UKF
(Sasiadek et al., 2008). The position of the robot
estimated by RBPF in the local map is considered to
be as an additional landmark (Thrun, 2000). When
the local map covariance matrix is fused to the
global map, the related data stays in the main
covariance matrix until the next time step (Thrun, et
al., 2003).
Figure 1 illustrates a block diagram of the sub-
mapping strategy using RBPF, UKF, and CLSF. The
strategy in this scheduling is to give the posterior
sate of the system at time step k (previously
NavigationofanAutonomousMobileRobotUsingDataAssociationMethod
305

estimated by RBPF) to the UKF algorithm in order
to make an individual map of the environment (the
global map). The local map estimated by RBPF is
partially used to make an estimation of the path.
This local map is then added to the CLSF algorithm,
where it is matched with the global map previously
estimated by UKF. A new map will be generated
based on CLSF algorithm to moment-match the
features estimated by each individual algorithm;
UKF and RBPF.
Figure 1: Scheduling without data association
incorporation in UKF.
Figure 2: Scheduling with data association incorporation
in UKF.
A modified scheduling technique is presented as
depicted in figure 2. Instead of updating the global
map using a straight forward mean, the ambiguity of
the data association is reduced using a data
association process algorithm to reduce a cluster of
information (Bar-Shalom, Fortmann, 1998). The
UKF is then using this modified posterior to
generate the global map. The rest of the process is
the same as what explained in figure 1. The main
difficulty in the mapping process would be to add
new landmarks into the map when global and local
maps are matched by CLSF. There is a need for a
proper formulation in order to make the mapping
process reliable (Guivant, Nebot, 2001). If a specific
measurement is insufficient to constrain the new
landmark in all dimensions, the decision to add a
new landmark could be quite challenging. In
Kalman-based algorithms, only a single
measurement is made to initialize a new landmark.
In the RBPF, each observation may be represented
in a Gaussian form (Montemerlo, Thrun, 2003) as:
z
k
~ N (
k
z
ˆ
+
k
(
ik ,
z
–
n
ik ,1
μ
), R
k
)
(5)
This Gaussian can be written as
|Z
~
2π|
1
i,k
exp [A . B]
(6)
A = –
2
1
(z
k
−
k
z
ˆ
−
k
(
ik ,
z
–
n
ik ,1
μ
))
T
(7)
B= R
1
k
(z
k
−
k
z
ˆ
−
k
(
ik ,
z
–
n
ik ,1
μ
))
(8)
Q is defined as a function equal to the negative of
the exponent of this Gaussian:
Q =
2
1
C . D
(9)
C = (z
k
−
k
z
ˆ
−
k
(
ik ,
z
–
n
ik ,1
μ
))
T
(10)
D = R
1
k
(z
k
−
k
z
ˆ
−
k
(
ik ,
z
–
n
ik ,1
μ
)
(11)
The second derivative of Q with respect to
ik ,
z
will
be the inverse of the covariance matrix of the
Gaussian in landmark coordinates.
,ik
z
Q
= − (z
k
−
k
z
ˆ
−
k
(
ik ,
z
–
n
ik ,1
μ
))
T
R
1
k
k
(12)
2
,
2
ik
z
Q
=
T
k
R
1
kk
(13)
As a result, an invertible observation can be used to
create a new landmark as
n
ik ,1
μ
=
h
1
(
n
x
R
k
, z
k
)
(14)
n
ik ,
=
T
k
R
1
kk
(15)
n
ŵ
k
=P
0
(16)
The initialization of landmarks may be calculated
through a simpler formulation. By setting the
variance of each landmark parameter to a high value
and incorporating the initial observation, the exact
initial covariance does not have to be considered.
Higher KG values lead the process to a more
accurate approximation regarding the observation of
each landmark (Thrun et al, 2000).
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
306

n
ik ,1
μ
=
h
1
(
n
x
R
k
, z
k
)
(17)
n
ik ,
= K I
(18)
4 SIMULATIONS AND RESULTS
Figure 3 illustrates specifications and dimensions of
the vehicle defined as A=3.00m, ℓ=2.00m,
W=0.70m, and B=0.2m. Speed of the vehicle is
assumed to be a constant but changing from 1m/s to
5m/s in different scenarios.
Figure 3: Mobile robot dimensions.
The vehicle is equipped with a range/bearing finder
device and capable of detecting 100 visible
landmarks in the environment. The maximum range
defined for the range/bearing device is assumed
40.00m. An encoder attached to the vehicle’s rear
tire measures its revolutions and infers the linear
displacement. An accelerometer is also used to
measure the change in heading. A combination of
heading and displacement measurements is
incorporated into the UHS algorithm in order to
dead reckon the vehicle location in the global frame
of reference. Figure 4 depicts a situation in which
the autonomous robot is travelling in a 100m by
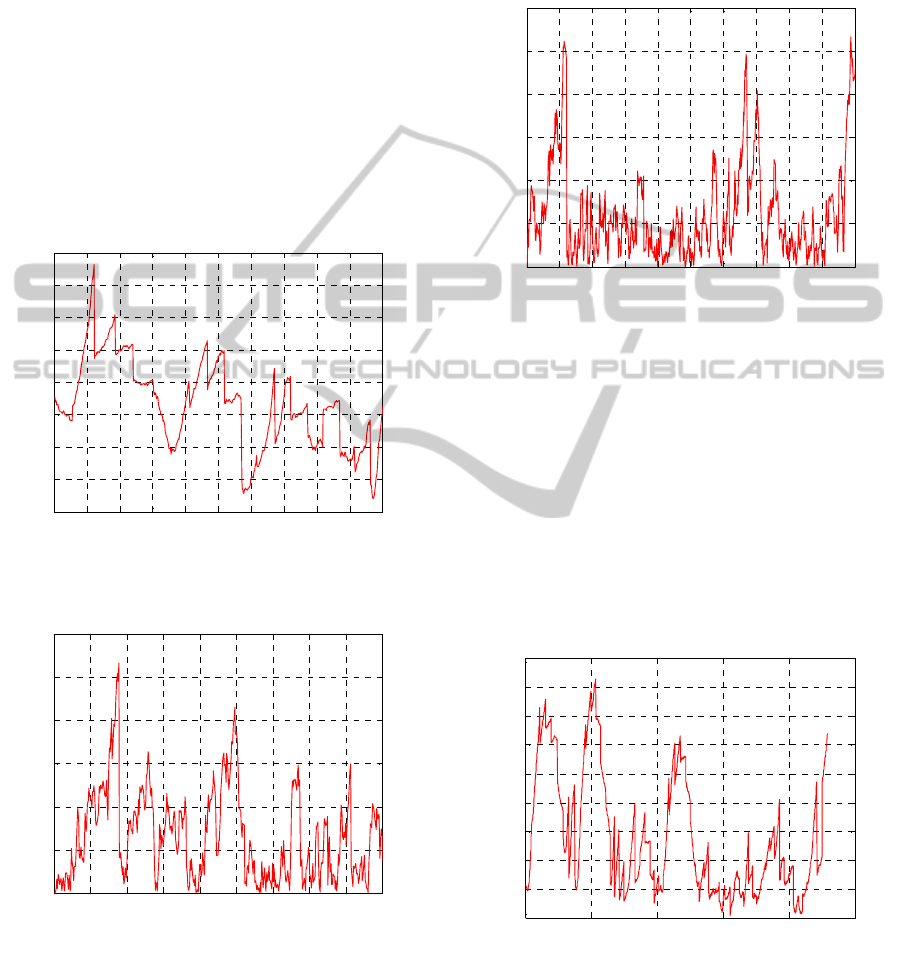
100m environment with a speed of 1m/s.
In order to compare two different scheduling
techniques, the RMS position error is depicted for
each situation. Figure 5 demonstrates the error in the
situation in which the data association is not
incorporated into the UKF map calculation. The
error in this case exceeds up to 0.5m. In figure 6, the
RMS position error fluctuations do not show much
of a difference if the data association process
interferes with the UKF map calculation. However,
the process time increases slightly (around 150s)
which indicates that adding the data association
calculation into UKF map building has its effect on
the process. Figures 7 and 8 depict the average
orientation error for both cases demonstrated in
figures 5 and 6. Results show that the error stays at
the same level (around 0.03rad) when the speed of
the vehicle is around 1m/s. It should be mentioned
that the system function that describes the
concurrent mapping of the environment is highly
non-linear. Furthermore, perturbations of the system
are quite hard to control due to a noisy
measurement. The significant amount of system
noise, affects the accuracy of map estimation
process. In real world applications, it is fair to
assume that both absolute and relative measurements
are functions of vehicle speed. As a result, the faster
the vehicle moves, the less accuracy is expected.
Figure 4: Autonomous robot travelling in a 100m×100m
square environment.
Figure 5: RMS position error for UKF mapping without
data association scheduling for ν=1m/s.
To further investigate the effect of data association
calculation on the mapping process, the speed of the
vehicle is set to 5m/s and the UKF mapping
calculation is done with and without influence of the
0 50 100 150 200 250 300 350 400 450
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Time (s)
RMS
P
os
i
ton
E
rror
(
m
)
NavigationofanAutonomousMobileRobotUsingDataAssociationMethod
307
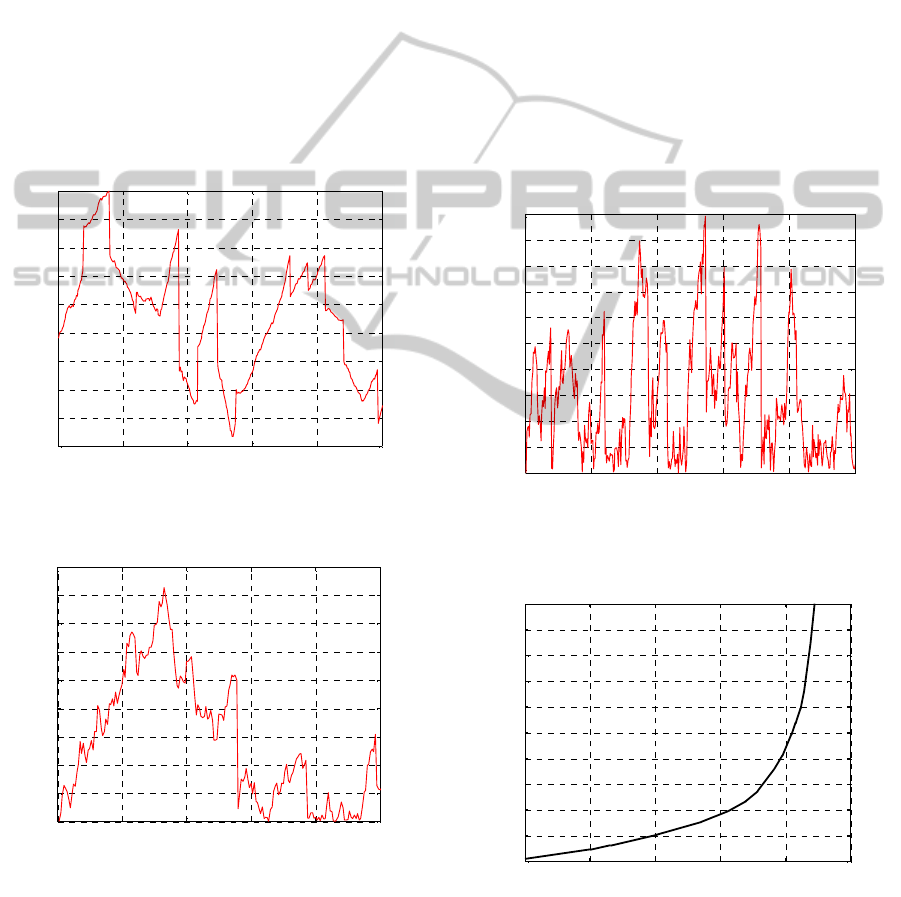
data association process. The average RMS position
error stays around 0.6m. The error is relatively
increased compared to the situation in which the
speed is 1m/s. It is expected to have such increase in
error because the accuracy of raw sensor data
extraction and converting it to lower dimensional
feature vector highly depends on the speed of the
vehicle which in turn, affects the accuracy of the
perception process. Figure 9 shows such increase in
error when the speed changes from 1m/s to 5m/s.
However, the increase in RMS position error is not
as much when the data association calculation is
influences the UKF mapping process. Figure 10
shows that as long as the UKF mapping stage takes
advantage of the data association process, the
change in speed would not affect the map accuracy.
Figure 6: RMS position error for UKF mapping with data
association scheduling for ν=1m/s.
Figure 7: Orientation error for UKF mapping without data
association scheduling for ν=1m/s.
The process time, however, increases substantially
which indicates that the mapping process is
consuming more than regular time when the data
association is processed in the UKF algorithm. The
same result is inferred from figures 11 and 12 in
terms of the orientation error. The orientation error
is not as much increased when the data association
process interfere the UKF mapping calculation once
the speed of the vehicle is increased to 5m/s.
Figure 8: Orientation error for UKF mapping with data
association scheduling for ν=1m/s.
One of the major reasons that the process time
increases is the computational power that is needed
to extract a real time image. Nowadays, current
CPUs are quite fast but not fast enough to provide
processing power for a real time application.
Depending on how much the data associated with
landmarks is incorporated into the map estimation
process, the demanding processing power for data
extraction varies. At a reasonable cost, a
compromise between the processing power and a
real time image must be considered.
Figure 9: RMS position error for UKF mapping without
data association scheduling for ν=5m/s.
A number of runs were performed and the UKF
estimated the global map at different speed. Figures
13 and 14 depict resulting RMS position error and
0 60 120 180 240 300 360 420 480 540 600
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Time (s)
RMS Positon Error (m)
0 50 100 150 200 250 300 350 400 450
0
0.02
0.04
0.06
0.08
0.1
0.12
Time (s)
Orientation Error (radians)
0 60 120 180 240 300 360 420 480 540 600
0
0.02
0.04
0.06
0.08
0.1
0.12
Time (s)
Orientation Error (radians)
0 40 80 120 160 200
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Time (s)
RMS Positon Error (m)
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
308
orientation error for two different scheduling. The
vehicle speed changes from 1m/s to 10m/s. As
illustrated in these figures, the error increases for
both scheduling techniques as the vehicle speed
increases. Ideally, at a low speed basis, the error
stays at the same level. Once the speed increases, the
performance of UKF with data association
calculation varies from the situation in which the
data association process does not influence the
global mapping estimation. At the speed of 5m/s
there is a substantial difference between two
techniques and this difference even grows at higher
speed sets. In practical situations, those scheduling
techniques may not always reflect the ideal
condition as plotted in figures 13 and 14. Other
factors such as system noise or device failures may
play major roles in the performance of the algorithm.
Figure 10: RMS position error for UKF mapping with data
association scheduling for ν=5m/s.
Figure 11: Orientation error for UKF mapping without
data association scheduling for ν=5m/s.
Nevertheless, the deterioration rate stays similar to
the ideal condition, meaning that, the higher the
vehicle speed is set to, the more erroneous
estimation is resulted. Figure 15 illustrates the
process time versus vehicle speed for both
scheduling techniques. Again, in low speed
conditions the effect of data association process on
the process time is negligible but as the vehicle
speed is added up, the process time increases
substantially. For relatively high speed situations,
the scheduling technique with the data association
influence in global mapping becomes nuisance even
though the error stays at a reasonable level. It should
be noted that one of the main intentions in a
scheduling technique is to bring the system enough
accuracy in estimation of the map and as close to
real time as possible. In order to achieve these goals,
an optimal point must be selected for each
scheduling technique. From figures 13 to 15 and for
this particular platform the map estimation
influences the UKF map calculation and with speed
set to 4m/s is the closest to the desired condition.
Figure 12: Orientation error for UKF mapping with data
association scheduling for ν=5m/s.
Figure 13: RMS position error for global map estimation
without data association technique for ν=1m/s to 10m/s.
It is interesting that the divergence between two
scheduling techniques occurs around 2m/s. This
0 80 160 240 320 400
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Time (s)
RMS Positon Error (m)
0 40 80 120 160 200
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
Time
(
s
)
Orientation Error (radians)
0 80 160 240 320 400
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
Time (s)
Orientation Error (radians)
0 2 4 6 8 10
0
1
2
3
4
5
6
7
8
9
10
RMS Position Error
(
m
)
Speed (m/s)
RMS Position Error vs. Speed Without Data Association Process
NavigationofanAutonomousMobileRobotUsingDataAssociationMethod
309
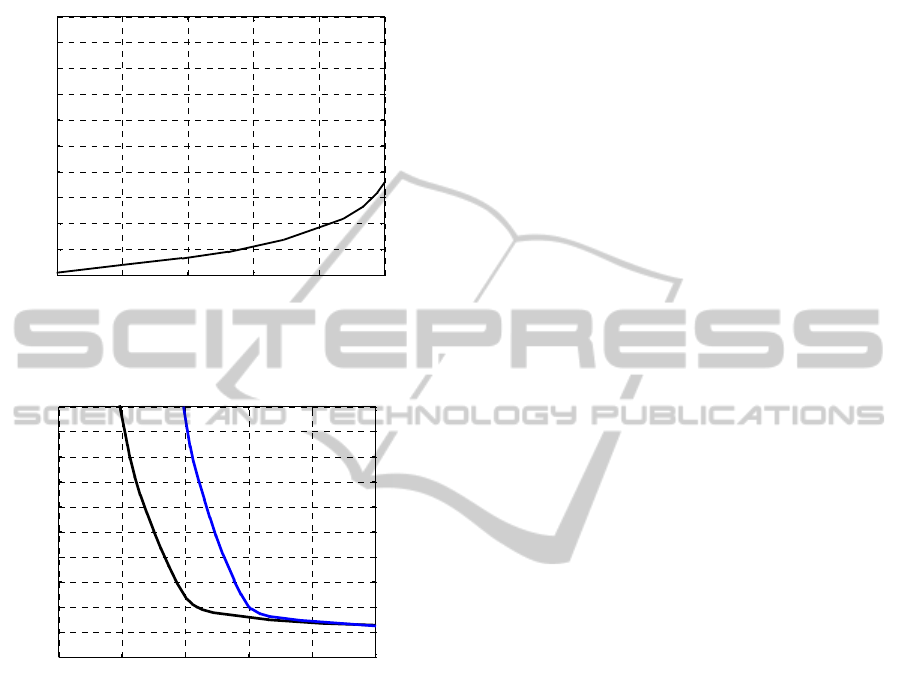
indicates that as long as the vehicle speed is
maintained around 2m/s, there is no need to use the
scheduling in the global map estimation by UKF.
Figure 14: RMS position error for global map estimation
with data association technique for ν=1m/s to 10m/s.
Figure 15: Computing time versus vehicle speed for
different scheduling techniques.
Once a specific combination of map accuracy and
process time is desired, depending on the
application, one can extract different variances of
the speed, time, and map accuracy. It is also evident
that for high speed settings, the data association
scheduling in the UKF map estimation process
causes an exponential increase in the process time.
5 CONCLUSION
In this paper, two different scheduling techniques
were briefly discussed and several mapping
scenarios were simulated via MATLAB and C++
codes for an autonomous robotic vehicle to map the
environment. The map accuracy through both
different techniques and in different settings was
discussed. Variations of each technique were
demonstrated in terms of Root Mean Square position
error and orientation error. In order to formalize the
mapping calculation, a data association process was
defined and applied for the global mapping
estimation using Unscented Kalman Filter. It was
concluded that depending on the application and in
order to get the best result, a compromise between
the process time and map accuracy is necessary. In
this particular scenario and for the specific platform
used in this study, the scheduling technique can be
used in global mapping estimation. The speed of the
vehicle in this case was set between 2m/s to 4m/s. It
was also concluded that for a desired accuracy, there
will be an unavoidable increase in the computing
time that is negligible for low speed settings.
However, if a shorter computing time is desired, a
decrease in vehicle speed setting is required.
ACKNOWLEDGEMENTS
A free software for robotics research was used in
this study. The software in form of both MATLAB
and C++ codes is available at http://www.lasmea.
univ-bpclermont.fr/ftp/pub/trassou/SLAM/SLAM_
Summer_School2002/SLAM%20Summer%20Scho
ol%202002.htm
REFERENCES
Durrant-Whyte H., Bailey T., 2006, Simultaneous
localization and mapping (SLAM): part I the essential
algorithms, IEEE Robatics and Automation Magazine,
Vol. 13, No. 2, pp. 99-108, June.
Smith R., Cheeseman P., 1986, The estimation and
representation of spatial uncertainty, International
Journal of Robotics Research, Vol. 5, Issue 4, pp. 56-
68.
Jaulin L., 2011, Range-only SLAM with occupancy maps:
A set-membership approach, IEEE Transaction on
Robotics, Vol. 27, Issue 5, pp. 1004-1010, May 31
st
.
Monjazeb A., Sasiadek J. Z., Necsulescu D., 2013,
Autonomous robot positioning using Unscented
HybridSLAM, Proc. International Conference on
Methods and Models in Automation and Robotics
(MMAR), pp. 588 – 593, Miedzyzdroje, Poland, 28-31
August.
Julier S. J., Uhlmann J. K., 2001, A counter example to the
theory of simultaneous localization and map building,
Proc. of IEEE International Conference on Robotics
and Automation, pp. 4238-4243, March.
Montemerlo M., Thrun S., Koller D., Wegbreit B., 2002,
“FastSLAM: A factored solution to the simultaneous
0 2 4 6 8 10
0
1
2
3
4
5
6
7
8
9
10
RMS Position Error
(
m
)
Speed (m/s)
RMS Position Error vs. Speed W ith Data Association Process
0 200 400 600 800 1000
0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Process Time
(
s
)
Speed (m/s)
Process Time vs. Vehicle Speed
With Data association
Without Data association
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
310

localization and mapping problem”, Proceedings of
AAAI National Conference of Artificial Intelligence.
Brooks A., Bailey T., 2009, HybridSLAM: Combining
FastSLAM and EKF-SLAM for reliable mapping,
Springer Tracts in Advanced Robotics, Volume 57, pp.
647-661.
Williams S. B., Dissanayake G., Durrant-Whyte H., 2002,
An Efficient Approach to the Simultaneous
Localisation and Mapping Problem, Proceedings of
the IEEE International Conference on Robotics &
Automation, Washington DC.
Sasiadek, J. Z., 2002, Sensor Fusion, Annual Reviews in
Control, IFAC Journal, pp. 203-228, No. 26.
Doucet A., Freitas N., Murphy K., Russell S., 2000, Rao-
Blackwellised particle filtering for dynamic Bayesian
Networks, Proceedings of Conference on Uncertainty
in Artificial Intelligence.
Bailey T., Nieto J., Nebot E., 2006, Consistency of
FastSLAM algorithm, Proceedings of IEEE
International Conference on Digital Object Identifier,
pp. 424-429.
Julier S. J., Uhlmann J. K., 2004, Unscented filtering and
nonlinear estimation, Proc. of IEEE Journal, Vol. 92,
Issue 3, pp. 401-422, March.
Negenborn R., 2003, Robot localization and Kalman
filters: on finding your position in a noisy world. MSc.
Thesis, Utrecht University, Netherland.
Monjazeb A., Sasiadek J. Z., Necsulescu D., 2012, An
approach to autonomous navigation based on
Unscented HybridSLAM, Proc. of 17
th
International
Conference on Methods and Models in Automation
and Robotics, pp. 369-374, Miedzyzdroje, Poland.
Monjazeb A., Sasiadek J. Z., Necsulescu D., 2011,
Autonomous navigation among large number of
nearby landmarks using FastSLAM and EKF-SLAM;
a comparative study, Proc. of 16
th
International
Conference on Methods and Models in Automation
and Robotics (MMAR), pp. 369-374, Miedzyzdroje,
Poland.
Lijun Z., Lianzheng G., Ke W., Ruifeng L., 2011, A
Hybrid SLAM method for service robots in Indoor
Environment, Proceedings of 30
th
Chinese Control
Conference (CCC), pp. 4034-4039, Yantai, China,
July.
Lindemann R. A. , Bickler D. B., Harrington B. D., Ortiz
G. M., Voothees C. J., 2006, Mars exploration rover
mobility development, IEEE Robotics and Automation
Magazine, pp. 19-26, Vol. 13, Issue 2.
Norgard M., Poulsen N., Ravn O., 2000, New
development in state estimation for nonlinear systems,
IFAC Automatica, pp. 1627-1638, Vol. 36, No. 11,
November.
Sasiadek J. Z., Hartana P., 2000, Odometery and sensor
data fusion for mobile robot navigation, Proceedings
of the 6
th
IFAC Symposium on Robot Control, pp. 531-
536, SYROCO.
Neira J., Tardos J., 2001, Data association in stochastic
mapping using the joint compatibility test, IEEE
Transactions on Robotics and Automation, pp. 890–
897, Vol. 17.
Sasiadek J. Z., Monjazeb A., Necsulescu D., 2008,
Navigation of an autonomous mobile robot using
EKF-SLAM and FastSLAM, Proc. of 16
th
Mediterranean Conference on Control and
Automation, pp. 517-522, Ajaccio, France.
Thrun S., 2000, Probabilistic algorithms in robotics, AI
Magazine 21, 4, pp. 93- 109.
Thrun S., Ferguson D., Haehnel D., Montemerlo M.,
Burgard W., Triebel R., 2003, A system for volumetric
robotic mapping of abandoned mines, Proceedings of
the IEEE International Conference on Robotics and
Automation (ICRA’03).
Bar-Shalom Y., Fortmann T., 1998, Tracking and data
association, Academic press, Inc.
Guivant J., Nebot E., 2001, Optimization of the
simultaneous localization and map building algorithm
for real time implementation, IEEE Transactions on
Robotics and Automation, 17(3):242–257.
Montemerlo M., Thrun S., 2003, Simultaneous
localization and mapping with unknown data
association using FastSLAM, Proceedings of the IEEE
International Conference on Robotics and
Automation, pp. 1985-1991, Vol. 2, September.
Thrun S., Fox D., Burgard W., 2000, Monte Carlo
Localization with mixture proposal distribution,
Proceedings of AAAI National Conference on
Artificial Intelligence, Austin, Texas, USA.
NavigationofanAutonomousMobileRobotUsingDataAssociationMethod
311
