
QoS based Resource Allocation and Service Selection in the Cloud
Rima Grati
1
, Khouloud Boukadi
1
and Hanêne Ben-Abdallah
2
1
Faculty of Economics and Management of Sfax, BP 1088, Sfax 3018, Tunisia
2
King Abdulaziz University, Jeddah, Saudi Arabia
Keywords: Web Service Selection, Resource Allocation, QoS Constraint, Cloud.
Abstract: Web service composition builds a new value-added web service using existing web services. A web service
may have many implementations, all of which have the same functionality, but may have different Quality
of Service (QoS) values. Hence, a challenging issue of web service composition is how to meet QoS and to
fulfil cloud customers’ expectations and preferences in the inherently dynamic environment of the Cloud.
Addressing the QoS based web service selection and resource allocation is the focus of this paper. This
challenge is a multi-objective optimization problem. To tackle this complex problem, we propose a new
Penalty Genetic Algorithm (PGA) to help a Cloud provider quickly determine a set of services that compose
the workflow of the composite web service. The proposed approach aims to, at the one hand, meet QoS
constraints prioritized by the Cloud customer and, at the other hand, respect the resource constraints of the
Cloud provider. To the best of our knowledge, this is the first attempt to handle the problem of the optimal
selection of web services while taking into account the resource allocation in order to guarantee the QoS
imposed by the Cloud customer and to maximize the profit of the Cloud provider. The experimental results
of Penalty Genetic Algorithm show that it outperforms the Integer Programming method when the number
of web services and the number of resources are large.
1 INTRODUCTION
Nowadays, web service composition is the ultimate
solution for building successful Software as a
Service application (SaaS) in the cloud environment
(Espadas et al., 2013). Recently, Cloud providers
have focused on developing SaaS that would be able
to effectively address different levels of customer
Quality of Service. In such context, introducing QoS
in service composition (i.e. SaaS application) raises
many challenges. Given a specific feature needed in
a service composition (abstract service), several
services (concrete services) realizing such a feature
may be available. All concrete services
corresponding to an abstract service are functionally
equivalent and thus the choice among them can be
dictated by QoS attributes. For instance, one may
decide to choose the cheapest service, the fastest, or
maybe a compromise between the two. Hence, given
a composition, a relevant problem is to determine
the set of concretizations (i.e., bindings between
abstract and concrete services) that satisfy the QoS
constraints imposed by the customer.
Furthermore, the deployment of a composite
service as a SaaS application in a cloud data centre
introduces new challenges for SaaS resource
management. Large-scale data centres usually
consist of thousands of physical machines
interconnected with network links. Virtualization
technology is used to guarantee simultaneous use of
resources in the physical servers. Thanks to the
virtualization technology, a physical server is sliced
into a number of virtual machines (VMs) (Qiang,
2010). These VMs are assigned as a chunk of their
physical servers' resources including processing
capacity, memory and storage and host the deployed
services. The VM must have sufficient capacities in
order to achieve the performance level of the
service, as dictated by the customer requirements.
Due to the dynamic environment of the cloud data
centre, where the workload of applications and the
resources capacities keep changing over time, the
placement of composite service is a challenging
issue (Yusoh et al., 2012). The SaaS provider should
consider the current resource capacities while
placing the composite service with the desired QoS.
It is not interesting to propose a good concretization
249
Grati R., Boukadi K. and Ben-Abdallah H..
QoS based Resource Allocation and Service Selection in the Cloud.
DOI: 10.5220/0005059602490256
In Proceedings of the 11th International Conference on e-Business (ICE-B-2014), pages 249-256
ISBN: 978-989-758-043-7
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

that reflects the QoS constraints imposed by the
customer while ignoring the placement as well as the
resource constraints.
Previous research papers for QoS aware
composition propose interesting applications of
constraint handling methods and search strategies
from operational or artificial intelligence research cf.
(Canfora et al., 2005; Li et al., 2013). However,
none of these approaches considers constraints on
provider related resources as a guarantee for the
desired QoS.
Our research question is as follows: Given the
abstract specification of a composite web service,
how can we select a web service implementation for
each of the tasks in the abstract specification so that
the overall QoS of the composition is optimal, whilst
accommodating constraints imposed by the provider
resources?
Finding a solution for this problem is NP-hard
(Yusoh et al., 2012) and the number of possible
combinations of web service implementations for
composite service grows as the number of tasks
involved in the composite service and the number of
web service implementations for each task increases.
In addition, the constraints on the provider resources
may make finding a feasible solution very difficult.
Therefore, scalable selection methods are necessary
to ensure a good quality composition solution in a
short time. To this end, different strategies can be
adopted like Integer Programming or meta-heuristic
optimization algorithms like Simulated Annealing or
Genetic Algorithms (GA).
The remaining of this paper is organized as
follows. Section 2 discusses the related work. The
problem formulation is described in Section 3.
Section 4 presents the proposed solution design
whose evaluation is discussed in Section 5. The
concluding remarks are presented in Section 6.
2 RELATED WORK
Several solutions to the service selection problem
have been reported (Canfora et al., 2005; Wada et
al., 2012; Wang et al., 2011). This problem consists
in determining the set of concretizations that satisfy
the QoS constraints imposed by the customer.
(Canfora et al., 2005)propose an approach based
on Genetic Algorithms to determine a set of concrete
services to be bound to the abstract services
composing the workflow of a composite service so
as to meet the QoS constraints established in the
SLA. Their approach aims also to optimize a
function of some other QoS parameters. In their
work, Canfora et al. do not address the selection of
the necessary amount of resources while selecting
the optimal service.
(Wada et al., 2012) propose an optimization
framework called Evolutionary multi objective
service composition optimizer (E3). E3 defines a
service deployment model and provides two multi
objective genetic algorithms (GAs): E3-MOGA and
Extreme-E3 (X-E3). Both of them produce a set of
Pareto solutions for service compositions that satisfy
the given SLAs. E3-MOGA and X-E3 determine
how many instances of each concrete service to be
selected in order to satisfy a certain SLA when a
definition of a workflow and a set of abstract
services are given. Similar to (Canfora et al., 2005)’s
approach, this one offers no means to select the set
of resources to run the selected services in order to
guarantee the QoS constraints. In addition the
proposed approach is not implemented on the cloud
environment.
(Wang et al., 2011) propose a QoS-aware service
selection approach which consists of two phases.
The first phase employs a cloud model to compute
the QoS uncertainty for pruning redundant services
while transforming the quantitative QoS to the
qualitative QoS for the QoS uncertainty
computation. The second phase aims to select the
optimal services based on the mixed integer
programming. Unlike our approach, this approach
does not consider the user preferences in their QoS
models. Besides, the service discovery ignores the
resource selection issue. In our approach, we define
weight values for each QoS using priority and the
selection of the optimal service taking into account
the resource allocation.
Yusoh et al. (Yusoh et al., 2012) present the
problem formulation and modelling of the multiple
composite SaaS component placement in the cloud.
They aim to reconfigure the initial placement by
clustering the components, for instance the new
placement can minimize the resources used while
satisfying the SaaS SLA. In order to address this
issue, a Grouping Genetic Algorithm (GGA) has
been proposed and implemented. The SaaS
placement approach tries to allocate the adequate
resource in order to guarantee the SLA. This way of
thinking is similar to our work. However, in their
work, the SaaS application is considered as a black
box (i.e a well-defined application) while in our
work we consider both the dynamic selection
services as well as the discovering resources that
meet the QoS constraints. In addition, in their
approach, the authors consider the response time of
the SaaS only as the SLA attribute. Unlike our
ICE-B2014-InternationalConferenceone-Business
250

approach, we consider the response time, the cost,
the reliability and the throughput and we also
consider a weight for each QoS Characteristics.
Linlin et al. (Linlin et al., 2011)propose a
resource allocation algorithms for SaaS providers
who want to minimize infrastructure cost and SLA
violations. The proposed algorithms are designed in
a way to ensure that SaaS providers are able to
manage the dynamic change of customers, mapping
customer requests to infrastructure level parameters
and handling heterogeneity of VM. They design and
implement scheduling mechanisms to ensure the
following issues. The scheduling mechanism
determines where and which type of VM has to be
initiated by incorporating the heterogeneity of VMs.
Unlike our approach, this approach does not
consider the service discovery.
Several approaches have been proposed to deal
with the resource allocation problem based on the
application workload (Zhu and Agrawal, 2012;
Papagianni et al., 2013; Karakoc et al., 2006;
BangYu et al., 2007). In our review, we will not
present these works, since they tackled only the
resource allocation and neglected the service
concretization problem. To the best of our
knowledge, this is the first attempt to handle the
service selection and the resource allocation in the
cloud to guarantee the QoS constraint of the cloud
customer and his preferences expressed by a weight
for each QoS Characteristic.
3 PROBLEM FORMULATION
Our work aims to propose an approach for cloud
provider to quickly determine, using a PGA, a set of
concrete services to be bound to abstract services
composing the workflow of a composite service.
The binding must:
1. Meet the QoS constraints expressed by the
cloud customer. For example, the customer
can have multiple QoS constraints for a
composite service, such as minimal response
time and price, maximal availability and
reliability simultaneously;
2. Optimize a function of some QoS
Characteristics. The customer may want to
minimize the response time while keeping
the cost below a limit. The customer may
also have preferences for the QoS
characteristics, which can be expressed in
terms of weighting of preferences; and
3. Meet the resource constraints of the
provider's IT infrastructure. For all service
components placed in a virtual machine, the
total requirements of the composite service
must not exceed the VM's capacities which
are defined by processing, memory, network
as well as storage capacities.
According to the above requirements, we
formulate the problem as follows:
A= {A
1
, A
2
, A
3
, A
4
,... A
n
} is a set of abstract
services involved in a composition scenario
where n is the total number of web services in
the composition;
Si = {S
i1
, S
i2
, S
i3
, S
i4
,... S
im
} is a set of
concrete services Si for each of the abstract
service A
i
where and m is the total number of
services for abstract service A
i
.
3.1 Concrete Services Related
Constraints: SC
We define the Concrete services related Constraints
by:
v
,v
,v
, and v
are the QoS Characteristic
values for concrete web service S
ij
.
M
Sij
is the Memory requirement for concrete
service S
ij
.
T
Sij
is the task size of concrete service S
ij
.
S
Sij
is the storage requirement of concrete
service S
ij
.
3.2 Customer Related Constraints: CC
We define the set of QoS Constraints imposed by the
Customer by CC where the inequality CC(X) 0
(Coello, 2010). The QoS constraints are assertions
on the overall values of QoS characteristics, e.g.:
Cost < 50 and ResponseTime < 100.
We consider w1, w2, w3, and w4 as the weights
for QoS characteristics: response time, cost,
reliability and throughput where:
∑
w
1
(1)
3.3 Resources related Constraints: RC
We consider R= {r
1
, r
2
, r
3
,…r
k
}as the set of
resources available within a Cloud Provider Data
centre where r
k
∈ R is the r
virtual machine (or
resource). Each resource r
k
is defined by four basic
attributes: M
rk
, S
rk
, P
rk
and U
rk
where:
M
rk
: is the Memory capacity of the resource r
k
.
QoSbasedResourceAllocationandServiceSelectionintheCloud
251

M
rkt
: is the Memory capacity of the resource
rk
at time t.
S
rk
: is the Storage capacity of the resource r
k
.
S
rkt
: is the Storage capacity of the resource rk
at time t.
P
rk
: is the Processing capacity of the resource
r
k
.
P
rkt
: is the Processing capacity of the resource
rk at time t.
U
rk
: is the Utilization rate of the resource r
k
.
U
rkt
: is the Utilization rate of the resource rk at
time t.
We define the set of resource capacities
constraints by the following constraints. The first
one is imposed on the memory capacity if the plan X
(the concrete web service) is placed on the
resourcer
. The second one is related to the storage
capacity. The last one concerns the processing
capacity.
∃r
∈RM
∈
M
M
|P
X
rk
(2)
∃r
∈R/S
∈
S
S
(3)
∃r
∈R/P
∈
P
P
(4)
The total response time of the candidate
composite web service is defined based on three
essential attributes: (i) the set of rules proposed by
(Cardoso, 2002) to compute all the possible paths
within the composite service, (ii) the processing time
of the candidate composite service in a selected
resource r, and (iii) the sum of the different paths.
By relying on these attributes the response time RT
(X) is determined. The RT must not exceed the
response time imposed by the customer. This
constraint is defined as:
∃
∈/RTX
(5)
The utilization rate of the resource r where the
plan X is executed should not be overloaded.
∃
∈/
100%
(6)
So, the problem is to find X (x
1
, x
2
, x
3
, x
n
),
meaning abstract web service A
i
uses concrete
service S
ix
such that:
∗
∗
(7)
Where F(X) is maximal subject to SC, CC and
RC (Concrete services-related Constraints,
Customer-related Constraints, and Resource-related
Constraints respectively), Function F(X) returns the
overall score of the web service selection plan X, in
which:
V
= max (v
,v
,v
…..v
: the
internal v
,v
,v
…..v
in the max
function refers to all values from the
considered QoS vectors referring to the
relevant QoS characteristic l. V
denotes the
maximal value of the l
th
QoS characteristic
(1l4),
V
denotes the minimal value of the l
th
QoS
characteristic (1l4),
V
X is the value of l
th
QoS Characteristic of
the composite service under the web service
selection plan X.
The chosen objective function for an individual
X is based on the simple additive weight method for
multiple QoS proposed by Jaeger in (Jaeger, 2006).
In the following part, we will discuss the design
of the penalty based GA to address the QoS-based
web service selection with constraints on the
underlying resources.
4 IMPLEMENTATION OF A
GENETIC ALGORITHM FOR
QoS BASED SELECTION IN
THE CLOUD
GA is a search heuristic that mimics the process
of natural selection where the survival of the fittest
is the major principal. In a genetic algorithm,
a population of candidate solutions (called
individuals, creatures, or phenotypes) to an
optimization problem is evolved toward better
solutions. Each candidate solution has a set of
properties (its chromosomes or genotype) which can
be mutated and altered. Applied to the selection
problem, an individual represents an assignment of a
candidate for each abstract service and thus can be
represented by a tuple. A population is a set of
ICE-B2014-InternationalConferenceone-Business
252
individuals and, thus, represents a set of concrete
service assignments. The fitness depicts a measure
that is considered by a genetic algorithm to select
individuals of the population for further evolution.
The problem formulated in section 3 is a
constrained optimization problem: how to achieve
the best QoS for a composite service while taking
into account the customer constraints (the optimality
issue), and how to ensure that a composite web
service satisfies the provider resources (the
resources responsible for achieving the desired
QoS). Traditionally GAs can only address
unconstraint problems. However, they can integrate
some constraints handling a method to take into
account constraints such as penalty function and
repairing methods among others(Coello, 2010). In
our work we propose a penalty based GA that
applies a penalty to an infeasible solution that
violates constraints.
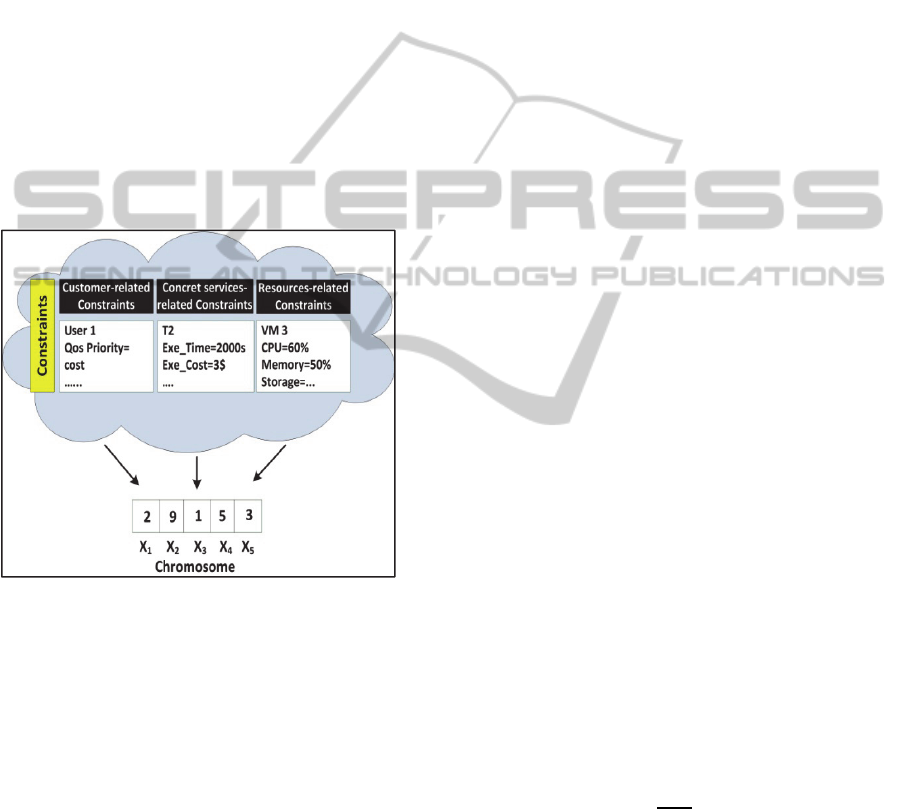
Figure 1: Problem encoding in the chromosome.
4.1 Chromosome Representation
To allow the GA to search for a solution, we first
need to encode the problem with a suitable
chromosome. In our case, the latter is represented by
an integer array with a number of items equals to the
number of distinct abstract services composing the
service. Each item, in turn, contains an index to the
array of the concrete services matching the abstract
service. Figure 1 shows an illustrative example of
the encoding procedure, where a composite web
service is represented by a chromosome with five
genes and having a set of constraints. In the
chromosome, X
1
=2 means the first abstract service
X
1
uses the second concrete web service from the
candidate web service set for the abstract web
service X
1
, and X
2
=9 means the second abstract
service X
2
uses the ninth concrete web service from
the candidate web service set for abstract web
service X
2
.
4.2 Infeasible Solutions
The chromosomes generated in a solution may be
infeasible due to some constraint violations. (See
Section 3 for the constraints). All the solutions that
do not comply with theses constraints are considered
as infeasible solutions, and their fitness value is
decreased by a penalty. The infeasible solutions
have less chance to survive in the evolution process
than feasible ones.
4.3 The Crossover and the Mutation
Operators
The crossover operator is the standard one-point
crossover (i.e., a single crossover point selects
randomly the parts of the two parents after the
crossover positions are exchanged to form two
offspring).
The mutation operator randomly selects an
abstract service (i.e., a position in the chromosome)
and randomly replaces the corresponding concrete
service with another one among those available.
4.4 The Fitness Function
In our work, the fitness function (8) is defined taking
into account two considerations: i) it should penalize
infeasible individuals in the sense that it should have
less fitness than a feasible one; and ii) it should
penalize more those individuals that violate more
constraints. We suppose that the penalty factors do
not depend on the current generation number in any
way, and therefore, remain constant during the entire
evolutionary process; that is, we adopt a static
penalty strategy as defined in equation (9).
Fitness Function= F(X)+P(X) (8)
P(X) =
0i
f
ϑ
X
0
0.9
,otherwise
(9)
Note that the proposed fitness function (equation
(8)) includes both the objective function defined in
section 3 and a penalty value P(X) given to the
individual X. The penalty function (equation (9))
adopts the most cited static penalty proposed by
Kuri morales in (Kuri Morales and C.V. Quezada,
1998), where ϑX is the total number of constraint
QoSbasedResourceAllocationandServiceSelectionintheCloud
253

violations of X, and ϑ
stands for the maximal
number of the constraint violations. According to the
fitness function, if an individual is feasible its
penalty value is 0. Otherwise, the penalty value is
computed based on the expression 0.9
,
which guarantees that more constraints an infeasible
individual violates, the higher penalty it has.
Besides, the value of the fitness function of a
fesasible individual is between 0 and 1, since the
objective function is in the range [0,1]. However an
infeasible individual’s fitness function is
F(X)0.9
, the value of which is less than 0,
which guarantee that an infeasible individual has
always less fitness value than any feasible one.
4.5 Penalty Genetic Algorithm
A penalty-based GA follows the same process as a
classic GA, its major specificity is the fitness
function which contains a penalty strategy to penalty
infeasible individuals that violate customer-related
constraints, concrete services-related constraints or
resources-related constraints or both. Figure 2depicts
the pseudo code of the PGA: the population is
initialized randomly. The fitness is computed for
each individual and the population then undergoes
the genetic operations and fitter individuals will be
copied in the next generation. This process will be
conducted iteratively until the termination condition
is met.
Figure 2: Pseudo code of the Penalty Genetic Algorithm.
5 EVALUATION
The Penalty GA described above has been
implemented using Java. Our evaluation covers three
factors: the number of composite services involved
in the problem, the number of concrete services for
each abstract service and the number of the available
resources in the data centre. These three parts of the
evaluation permit to determine how the variation of
the number of the three cited factors affects the
computation time and solution quality of the PGA.
These experiments show also the scalability and the
effectiveness of the Penalty GA (PGA) tested on a
number of problem instances with different sizes and
complexities. To better position our algorithm, we
compare its performance with the Integer
Programming method (IP) one.
The experiments were carried out on a desktop
computer with 3 GHz Intel Core 2 Duo CPU and
4GB RAM. The parameter settings for the PGA are
listed in Table 1. These parameters were obtained
through doing trials on randomly generated test
problems. We tested the PGA for 10 test cases
which represent combinations of the three factors
cited above. For the Integer Programming, we
performed each test case only once, because the
execution times and the solution found are fixed for
each test.
Table 1: Parameters setting for PGA.
Attribute Value/Condition
Population size 100
Initial population Randomly generated
solutions
Crossover probability 0,80
Mutation probability 0,10
Termination condition No improvement for the best
individual in 30 consecutive
generations
Test cases with different numbers of
composite web services
We build six tests by fixing the number of resources
and with different numbers of composite services
ranging from 5 to 30 with an increment of 5, each of
which has ten abstract services. From this test case,
we can construct the other four problems. This
experimentation shows how the quality of the
solution and the computation time of the PGA may
be affected by the number of composite web
services.
Figure 3 shows that the computation time, when
the number of composite service is small (5) Integer
ICE-B2014-InternationalConferenceone-Business
254

Programming outperforms PGA. For about 6
Composite services the performances of the two
approaches tend to be the same. Then, while the
PGA is able to keep its timing performance closely
to linear, the computation time of the Integer
Programming increases in super linear trend. So we
conclude that when we have a large number of
composite services, PGAs should be preferred
instead of Integer Programming. And in most cases,
the number of composed services is higher than 6.
Figure 3: the computation time of the PGA and IP when
varying the number of composite services.
Test problem with different numbers of
concrete services for each abstract service
We construct six tests with different concrete web
service by fixing the number of resources, the
number of composite web services and varying the
number of concrete web services from 5 to 30.
The growth trend of the computation time of the
Penalty GA, as the number of concrete services
increases, is shown in Figure 4. From the figure we
can see that when the number of concrete service is
small (5-9) Integer Programming exceeds PGA. For
about 10 concrete services the performances of the
two approaches tend to be the same. Then, while the
Penalty GA is able to keep its timing performance
almost constant, this is not the case for Integer
Programming, for which we see an exponential
growth. So we conclude that when we have a large
number of concrete services available for each
abstract service, GAs should be preferred instead of
Integer Programming. This will be the case of
widely used services, such as hotel booking, weather
services or e-commerce services. On the other hand,
whenever the number of concrete services available
is limited, Integer Programming is preferred. This
would be the case of very specific (e.g., scientific
computation) services.
Figure 4: the computation time of PGA and IP when
varying the number of concrete services.
Test problem with different resources
We construct six tests with different number of
resources by fixing the number of composite web
services, concrete web services and varying the
number of resource from 150 to 600 VMs with an
increment of 150. This experiment is an evaluation
of how the number of the resources affects the
computation time and solution quality of the Penalty
GA and Integer Programming. Figure 5visualizes the
computation time taken by the Penalty GA and the
Integer Programming for finding the solutions for
each of the test cases. It shows that when the number
of VM is small, the PGA and IP are similar, but
when the number of VM is up to 450 VMs, the GPA
grows slowly and outweighs IP which progresses
linearly.
Figure 5: Computation time of PGA and IP when varying
the number of VM.
6 CONCLUSION
This paper studied the application of penalty genetic
algorithms to the problem of QoS based web service
composition deployed on the cloud. It proposed and
developed a penalty genetic algorithm to address this
problem, which is characterized by complex, highly
0
50
100
150
200
250
5 1015202530
computation time (seconds)
Number of Composite Services
PGA
IP
0
20
40
60
80
100
120
0 5 10 15 20 25 30
Computation time
(seconds)
Number of concrete services
PGA
IP
0
50
100
150
200
250
150 300 450 600 750 900
Computation times
(seconds)
Number of reources
PGA
IP
QoSbasedResourceAllocationandServiceSelectionintheCloud
255

constrained and multi objective problem. More
precisely, our contribution allows SaaS provider to
quickly determine, using a penalty based GA, a set
of services (concrete services) to be bound to
abstract services composing the workflow of a
composite service. The binding both optimizes a
function of some QoS characteristics requested by
the customer with some weighing preferences, and
meets the resource constraints of the provider.
Indeed, for all service components placed in a virtual
machine, the total requirements of the composite
service must not exceed the VM's capacities. These
goals were successfully achieved by an evaluation
showing the effectiveness of the Penalty GA. To the
best of our knowledge, this is the first attempt to
handle the service selection and resource allocation
in a dynamic Cloud environment.
Based on our preliminary experimental results,
the proposed Penalty GA often produces a feasible
solution for all test problems. We are in the process
of conducting further experimental evaluations to
further confirm these results.
REFERENCES
Espadas, J.; Molina, A.; Jimeneza, G.; Molinab, M.;
Ramíreza, R. A tenant-based resource allocation
model for scaling Software-as-a-Service applications
over cloud computing infrastructures. Future Gener
Comput Syst. 2013;29(1):273-286.
Qiang, D. Resource allocation in buffered crossbar
switches for supporting network virtualization. High
Performance Switching and Routing (HPSR), 2010
International Conference on; 2010. p. 147-152.
Yusoh, M.; Izzah, Z.; Maolin, T. Clustering composite
SaaS components in Cloud computing using a
Grouping Genetic Algorithm. Evolutionary
Computation (CEC), 2012 IEEE Congress on; 2012. p.
1-8.
Canfora, G.; Penta, M.D.; Esposito, R.; Villani, M.L. An
approach for QoS-aware service composition based on
genetic algorithms. Proceedings of the 7th annual
conference on Genetic and evolutionary computation.
Washington DC, USA: ACM; 2005. p. 1069-1075.
Li, W.; Zhong, Y.; Wang, X.; Cao, Y. Resource
virtualization and service selection in cloud logistics. J
Netw Comput Appl. 2013;36(6):1696-1704.
Wada, H.; Suzuki, J.; Yamano, Y.; Oba, K. E3: A
Multiobjective Optimization Framework for SLA-
Aware Service Composition. IEEE Transactions on
Services Computing. 2012;5(3):358-372.
Wang, S.; Zibin, Z.; Qibo, S.; Hua, Z.; Fangchun, Y.
Cloud model for service selection. Computer
Communications Workshops (INFOCOM WKSHPS),
2011 IEEE Conference on; 2011. p. 666-671.
Linlin, W.; Garg, S.K.; Buyya, R. SLA-Based Resource
Allocation for Software as a Service Provider (SaaS)
in Cloud Computing Environments. Cluster, Cloud
and Grid Computing (CCGrid), 2011 11th IEEE/ACM
International Symposium on; 2011. p. 195-204.
Zhu, Q.; Agrawal, G. Resource provisioning with budget
constraints for adaptive applications in cloud
environments. Vol. Vol 5, IEEE Transactions on
Services Computing; 2012. p. 497–511.
Papagianni, C.; Leivadeas, A.; Papavassiliou, S.; Maglaris,
V.; Cervello-Pastor, C.; Monje, A. On the optimal
allocation of virtual resources in cloud computing
networks. Computers, IEEE Transactions on.
2013;62(6):1060-1071.
Karakoc, E.; Kardas, K.; Senkul, P. A Workflow-Based
Web Service Composition System. Web Intelligence
and Intelligent Agent Technology Workshops, 2006
WI-IAT 2006 Workshops 2006 IEEE/WIC/ACM
International Conference on; 2006. p. 113-116.
BangYu, W.; Chi-Hung, C.; Zhe, C. Resource Allocation
Based On Workflow For Enhancing the Performance
of Composite Service. Services Computing, 2007 SCC
2007 IEEE International Conference on; 2007. p. 552-
559.
Coello, C.A.C. Constraint-handling techniques used with
evolutionary algorithms. Proceedings of the 12th
annual conference companion on Genetic and
evolutionary computation. Portland, Oregon, USA:
ACM; 2010. p. 2603-2624.
Cardoso, J. Quality of service and semantic composition
of workflows [USA]: University of Georgia, Athens;
2002.
Jaeger, M. Optimising Quality of Service for the
composition of electronic services [Berlin]:
Technischte Universit; 2006.
Kuri Morales; C.V. Quezada. A universal eclectic genetic
algorithm for constrained optimization. 6th European
Congress on Intelligent Techniques and Soft
Computing, EUFIT’98. Verlag Mainz, Aachen,
Germany; 1998. p. 518–522.
ICE-B2014-InternationalConferenceone-Business
256
