Reconﬁgurable Priority Ceiling Protocol

Under Rate Monotonic Based Real-time Scheduling

Maroua Gasmi

1,2

, Olfa Mosbahi

, Mohamed Khalgui

and Luis Gomes

Computer Science Departement, Faculty of Science of Tunis, University Tunis el Manar, Tunis, Tunisia

Computer Science Departement, LISI Lab, INSAT Institute, University of Carthage, Tunis, Tunisia

Departamento de Engenharia Electrotcnica, Faculdade de Ciłncias e Tecnologia,

Universidade Nova de Lisboa, Caparica, Portugal

Keywords:

Real-time System, Reconﬁguration, Scheduling, Resource Sharing, Priority Ceiling Protocol.

Abstract:

This research paper deals with reconﬁgurable real-time systems to be adapted to their environment under user

requirements. A reconﬁguration scenario is a run-time software operation that allows the addition, removal

and update of real-time OS tasks which can share resources and should meet corresponding deadlines. We

propose a new Reconﬁgurable Priority Ceiling Protocol (denoted by RPCP) that avoids deadlocks after any

reconﬁguration scenario and changes the priorities of tasks in order to reduce their response and blocking

times, and to meet their deadlines. This protocol requires the use of two virtual processors in order to guarantee

the non-interruption of execution during the reconﬁguration step. We develop a tool that encodes this protocol

which is applied to a case study.

1 INTRODUCTION

Real-time constraints (Stankovic, 1996) are common

bases to most of the actual embedded systems (Lee

et al., 2007), since the latter have many time require-

ments imposed on their activities. These systems

follow a deﬁnite classiﬁcation (Colnaric and Verber,

2007). The functions performed by the real-time sys-

tems, are consistently, executed by a ﬁxed number of

tasks. Nevertheless, the notion of time is what makes

the difference between real-time and non-real-time

systems. The main rule is that the preeminent param-

eter, the deadline, has to be met under even the worst

circumstances (Kalinsky, 2003). In the case where

several tasks share a speciﬁc number of resources,

many issues can occur preventing these tasks from

meeting their deadlines. In the perspective of solving

these problems, Rate Monotonic schedule (Lehoczky

et al., 1989), is a scheduling algorithm that assigns

priorities on the basis of the period of the task. Al-

though, this algorithm, solves the mentioned prob-

This research paper is a collaboration between LISI

Lab (INSAT at University of Carthage in Tunisia), PASRI

(Ministry of High Study and Research in Tunisia) and Uni-

versidade Nova de Lisboa in Portugal. It is ﬁnancially sup-

ported as a MOBIDOC grant from the European Commis-

sion. We thank Mr. Wael Bouslama for his fruitful collabo-

ration in the experimental part.

lems, others can occur as a consequence. In fact, a

high priority task can be interrupted by a lower prior-

ity one, inverting the priorities of the two tasks (Sha

et al., 1990). This problematic scenario, called pri-

ority inheritance, is solved by dint of a synchroniza-

tion protocol called priority ceiling protocol (PCP).

Furthermore, a real-time system has the ability to

be reconﬁgured according to its surroundings (Bren-

nan et al., 2002). In fact, a reconﬁguration consists

on modifying the behavior of the system depending

of the modiﬁcations that occurred in its environment

(Wang et al., 1995). The reconﬁguration can either be

static, where it is only applied ofﬂine before the start-

ing of the system, or dynamic (Stewart et al., 1997).

The dynamic form of reconﬁguration can be either

manual (applied by a user) or automatic (applied by

intelligent agents within the system). In the literature,

the concept of reconﬁguration that we are introduc-

ing in this paper is indicated as a mode change since a

system is able to move from one mode of execution to

another. A mode change is deﬁned as the removal of

tasks, the addition of new ones and the change of their

parameters (Sha et al., 1989). As a matter of fact, the

particularity of the work that we propose in this paper

lies, essentially, in the possibility of reconﬁguring the

resources as well as the set of tasks, optimizing the

blocking times and lowering the response times after

Gasmi M., Mosbahi O., Khalgui M. and Gomes L..

Reconﬁgurable Priority Ceiling Protocol - Under Rate Monotonic Based Real-time Scheduling.

DOI: 10.5220/0005060900420052

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 42-52

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

each scenario of reconﬁguration. However, several

authors treated the mode change, proposing different

techniques. None of these techniques offers the ad-

vantages previously mentioned. In (Real and Crespo,

2004) the authors present a classiﬁcation and an eval-

uation of mode change protocols for single-processor,

ﬁxed priority, preemptively scheduled real-time sys-

tems. The contribution in (Stoimenov et al., 2009)

consists on presenting a method for timing analysis

of single-processor multi-mode systems with earliest

deadline ﬁrst (EDF) or ﬁxed priority (FP) scheduling

of tasks. In (Tindell et al., 1992) the mode changes are

deﬁned either as operations increasing a task sets pro-

cessor utilization, or operations that decrease it. The

analysis approach in the latter work is improved and

extended to deadline-monotonic scheduling in (Pedro

and Burns, 1998). The model is augmented with tran-

sition offsets in (Pedro and Burns, 1998), which per-

mits to avoid overload situations. In the idle time

protocol (Tindell and Alonso, 1996), when a mode

change request occurs, the activation of the new tasks

is not done until the next idle instant takes place. Al-

though its implementation is simple, the latter proto-

col is considered to be poor when it comes to prompt-

ness. The ceiling protocol in Multi-Moded Real-Time

Systems (Farcas, 2006) is an approach that combines

the mode changes and permits an important degree of

ﬂexibility with immediate inheritance priority ceiling

protocol (IIPCP). In the works presented in (Gharbi

et al., 2013; Gharbi et al., 2011; Khalgui et al., 2011)

the Priority Ceiling Protocol (PCP) is applied as an

approach to ensure the scheduling between periodic

tasks but the change of priorities of these tasks in

order to minimize the response time reconﬁguration

is not taken into account. Generally speaking, in a

random scenario of reconﬁguration, the problems of

deadlock and exceeding of deadline can occur. No

one in the related works treated this situation where

we can have activations of resources and tasks. we

propose an original solution, denoted as Reconﬁg-

urable Priority Ceiling Protocol (RPCP) to the pre-

viously deﬁned problems, in addition to the optimiza-

tion of blocking and response times. To guarantee the

non interruption of execution after any reconﬁgura-

tion scenario, the proposed solution starts by separat-

ing the physical processor into two virtual ones. The

ﬁrst continues the regular execution of PCP, while the

second one calculates the new periods and therefore

priorities that guarantee the previously deﬁned opti-

mizations. We developed a simulation tool at LISI

Lab (University of Carthage) which is applied to a

case study in order to show the contributions of the

paper.

The following section gives an overview on the dif-

ferent axes that create the context of the work. the

section case study takes an example of reconﬁgurable

tasks and resources and shows the impact of the ran-

dom reconﬁguration on causing issues in the sys-

tem. After that, we formalized the elements that form

mathematically our environment. Then we explain

our contribution step by step and ﬁnish by presenting

the proposed algorithm and exposing the simulation.

2 BACKGROUND

A real-time task (Liu and Layland, 1973), designated

in this paper as τ

, is essentially characterized by its:

(i) Arrival time A when τ

becomes ready for execu-

tion, (ii) Computation time C known as Worst Case

Execution Time (WCET), this parameter has to be de-

termined previously, (iii) Deadline D is the time limit

by which τ

must be accomplished, (iv) Starting time

S is the moment when the system decides to start τ

Indubitably, it cannot be earlier than the arrival time

A as before this time the task is totally unknown, (v)

Finish time E is the time when the execution of τi

ﬁnishes. It can be depicted by the sum of the start-

ing time S and the computation time C, (vi) Period T

which serves as a duration of one cycle on a repeating

execution of a periodic task and represents the interval

between two consecutive activations. It is important

to mention that in the case of an aperiodic task, the

concept of period is utterly missing, (vii) Work Left

W is the work left for a task to execute and ﬁnally

(vii) response time R is the length of time from the

moment of release to the instant when the task com-

pletes its execution. This time is given by the follow-

ing formula (Tokuda et al., 1990):

= 0, R

= C

+ B

∑

j>k

q−1

The response time of a task, denoted as R

, is ob-

tained once R

= R

q+1

. During its execution,

a task is able to use one or several resources, refer-

ring by the latter to any shared hardware or software

object (Mok et al., 2001). The execution runs reg-

ularly, until the moment when several tasks wish to

use a single resource (Lipari and Bini, 2003). It is

necessary to mention that a blocking can be caused

when several tasks wish to access a single resource

(Tokuda et al., 1990). Here comes the role of the real-

time scheduling. Its main goal is to assign processors

and resources to tasks in such a way that all the im-

posed constraints are respected. Among the schedul-

ing algorithms, Rate Monotonic scheduling (Liu and

Layland, 1973) occupies an important role. It assigns

ReconfigurablePriorityCeilingProtocol-UnderRateMonotonicBasedReal-timeScheduling

priorities in a static way: the shorter the period of the

task the higher its priority. In (Sha et al., 1990) the

authors prove that this scheduling protocol is optimal

among the rest of static policies . One major limita-

tion of ﬁxed-priority scheduling is that it is not always

possible to fully utilize the CPU (Sha et al., 1990).

The schedulability test for RMS is:

U =

∑

i=1

≤ n ∗ (2

− 1)

In a system with shared resources, it is impossible

to eliminate all priority inversions but it is possible

to limit the waiting time to minimize time and pre-

dict blocks. For this, several approaches are intro-

duced. PCP prevents the deadlock situation as well

as chained blocking (Sha et al., 1990). The rules in

PCP aim essentially to prohibit a task to enter the

critical section if there were any semaphores that may

block this task. This protocol supposes that every task

has a ﬁxed priority and the used resources are known

before the starting of the execution (Chen and Lin,

1991). In this protocol each resource is assigned a

priority ceiling, which is a priority equal to the high-

est priority of any task which may lock the resource.

Hence, it should be taken into consideration that un-

der the priority ceiling protocol, a task is blocked at

most once, by a lower priority task, for the duration

of a critical section, no matter how many tasks con-

ﬂict with it. With the given information in (Liu et al.,

2000), computing the maximum blocking time Bi for

a task is possible. Above all else, we should point out

that blocking time, when using PCP in particular, may

arise under 3 possibilities: Directly blocked tasks, In-

heritance blocked tasks or Avoidance blocked tasks.

Therefore, the proposed protocol RPCP is based upon

both RM and PCP since the ﬁrst is optimal and the

second is useful for shared resources; In fact, it is cus-

tomized to ﬁt the feasibility test and the condition im-

posed by RM. Besides, the particularities of this pro-

tocol lie in its ability to change priorities, reconﬁgure

both tasks and resources and minimize the response

as well as the blocking times.

3 CASE STUDY

We present in this section a case study to expose our

problem, and to be assumed in the following as a run-

ning example. Let us consider a system to be sched-

uled by both PCP and RM, and to be implemented by

OS tasks with shared resources. The details related

to these tasks are given by Table1. The task τ

for

example is periodically executed each 60 time units,

and uses the resource R1 for 5 time units.

Table 1: Parameters of the initial tasks.

Tasks Priorities Resources Computation times (Ci) Periods (Ti)

P1 R1 5 60

R1 2

R2 3

P3 R2 5 50

R5 2

45R6 3

R8 2

R6 4

R7 3

According to the simulator Cheddar (Singhoff et al.,

2004), the system is feasible since all the tasks meet

the related deadlines as depicted in Figure 1. We can

prove the system feasibility by applying the RM con-

dition

∑

i=1

= 60% and is lower than 5 ∗ (2

− 1) =

74%. We are interested in the current work in the soft-

ware reconﬁguration of tasks and resources. A recon-

ﬁguration is assumed to be an operation allowing the

addition-removal of tasks or resources. No one in all

related works dealing with real-time scheduling treats

this form of reconﬁguration. Let we assume the fol-

lowing reconﬁguration that adds the tasks τ

and τ

and removes τ

and τ

under well-deﬁned conditions

described in user requirements.

Figure 1: Execution graph of the tasks.

Table 2 depicts in detail the new conﬁguration of the

system.

Table 2: Parameter of the tasks after reconﬁguration.

Tasks Priorities Resources Computation times (Ci) Periods (Ti)

R1 8

R4 12

R1 15

R2 5

R2 3

R3 17

R3 14

R4 6

R4 2

R1 18

Note that this reconﬁguration scenario can allow the

violation of real-time properties or block and destroy

the whole system in some situations, since the new

tasks have higher priorities and the old ones have to

use new resources. We show in Figure 2 the run-time

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

problem that occurs in the system after this reconﬁg-

uration scenario. In fact, while τ

is holding the re-

source R

, the reconﬁguration adds the resource R

the list of the resources belonging to the latter task.

, the task added after the application of this sce-

nario, ﬁnishes the execution of R

and keeps waiting

for R

as shown in Figure 2. A deadlock happens in

this situation.

Figure 2: Deadlock due to the reconﬁguration scenario.

The random application of the new conﬁguration

causes a deadlock leading automatically to the vi-

olation of the feasibility conditions. In the related

works the deadlock problem was cured but without

taking into account the optimization of the compu-

tation time neither the possibility of minimizing the

blocking times and the response times of the different

tasks. The addition and removal of resources within

the system as well as changing the priorities of the

tasks are original particularities in our work that we

cannot ﬁnd in other works.

In this section, the remarked problem is essentially

due to an arbitrary choice of priorities after a recon-

ﬁguration scenario. For this reason, we introduce in

this paper, a new solution that does not only consist on

preventing any deadlocks owing to a sudden change

in the set of tasks caused by an incoming reconﬁgura-

tion, but also on drafting suitable priorities that offer

minimal blocking times for each task.

4 FORMALIZATION

In this section, we are interested in mathematically

deﬁning the elements of the system and their reactions

to any reconﬁguration scenario as well as the pro-

posed representation of their characteristics. Hence,

in addition to the existing parameters, mentioned in

the section background, we propose to add the fol-

lowing new ones to each task. (i) π(t): the state of

a task within the system (1 if the task is active either

executed or not, 0 else). (i) σ: the set of possible re-

sources that can be used by the task, (ii) Res(t): the

set of resources used by the task at t, (iii) Cond(t):

state of conditions (1 if the condition that activates

the task is met at t, 0 if not) and (iv) Request(t): the

set of resources required by the task at t. Let τ

Sys

and

Sys

respectively be the set of all possible tasks and

resources that may be executed within the system in-

dependently from the time. Therefore, a general sys-

tem that describes the global environment, denoted as

Sys, is deﬁned by the previously mentioned couple.

Sys = (τ

Sys

) (1)

Running example1:

Through the example given in the case study τ

Sys

and R

Sys

are expressed as follows:

Sys

= {τ

,τ

}

Sys

= {R

}

Let τ

Sys

(t) and R

Sys

(t) respectively be the set of active

tasks and resources within the system at a given mo-

ment t. Pointedly, the set of active tasks , denoted as

Sys

(t) at the moment t is represented by the group of

tasks whose the state is set to be active. This assort-

ment is given by the following formula:

Sys

(t) = {τ

∈ τ

Sys

/τ

.π(t) = 1} (2)

Respectively, the group of resources which are active

at t , denoted as R

Sys

(t), is represented by the re-

sources required by the active tasks at that moment.

This set of resources is given by the following for-

mula:

Sys

(t) = {R

∈ R

Sys

/∃τ

,τ

.π(t) = 1 ∧ R

∈ τ

.Request(t)}

(3)

As a consequence, the general system at that moment,

denoted as Sys(t), is deﬁned by the previously men-

tioned couple.

Sys(t) = (τ

Sys

(t), R

Sys

(t)) (4)

Running example 2:

Through the example given in the case study, Ta-

ble1 contains the list of the active tasks and re-

sources at t

before the application of the recon-

ﬁguration scenario. As a consequence, τ

Sys

)

and R

Sys

) are expressed as follows:

Sys

) = {τ

,τ

}

Sys

) = {R

}

According to user requirements, each reconﬁguration

scenario is automatically applied to add or remove

tasks from a system at a speciﬁc moment denoted as

. In fact, the couple τ

Sys

) and R

Sys

) that takes

place at t

, which is a moment coming right before the

ReconfigurablePriorityCeilingProtocol-UnderRateMonotonicBasedReal-timeScheduling

reconﬁguration, is replaced by τ

Sys

) and R

Sys

Let ξ

Sys

),described by the formula (5), be the group

of tasks to be added to the system. In fact, a task is

ready to be added when the condition that activates it

is met at t

Sys

) = {τ

∈ τ

Sys

/τ

.Cond(t

) = 1} (5)

Let ∆

Sys

),described by the formula (6), be the

group of tasks to be removed from the system. Simi-

larly, a task is ready to be removed when the condition

that deactivates it is met at t

∆

Sys

) = {τ

∈ τ

Sys

)/τ

.Cond(t

) = 0} (6)

Thereby, the new set of active tasks at t

after re-

conﬁguration is expressed as the addition of the tasks

Sys

) and the removal of the tasks ∆

Sys

) from the

old set of tasks established at t

. The formula describ-

ing τ

Sys

) is given as follows:

Sys

) = τ

Sys

) ∪ ξ

Sys

) \ ∆

Sys

) (7)

Running example 3:

Through the example given in the case study, the

changes from Table1 to Table2 represent a recon-

ﬁguration scenario that occurred in t

. In fact, the

actions of addition and removal of tasks are per-

formed. In our case, the added tasks (ξ

Sys

))

and the removed ones (∆

Sys

)) are given as fol-

lows:

Sys

) = {τ

,τ

}∆

Sys

) = {τ

,τ

}

Subsequently, the new set of active tasks after

reconﬁguration (τ

Sys

)) is expressed as follows:

Sys

) = τ

Sys

) ∪ ξ

Sys

) \ ∆

Sys

) =

{τ

,τ

}

Likewise, the subset of resources can be modiﬁed by

the reconﬁguration. Let ξ

) ,described by the for-

mula (8), be the group of resources to be added to the

system. In fact, a resource is considered to be active

when it is added to the system as required by a task

added through ξ

Sys

) = {R

∈ R

Sys

/∃τ

∈ ξ

Sys

)∧R

∈ τ

.Request(t

)}

(8)

However, the list of resources which need to be deac-

tivated is described by the ones that are no longer re-

quired by any task. It is to mention, that if a resource

is shared by several tasks, it cannot be removed when

some of them are removed. The group of resources

which cannot be removed is denoted by ∆

) and

described by the formula (9).

∆

) = {R

∈ R

Sys

)/∃τ

∈ τ

Sys

) \ ∆

Sys

∈ τ

.Request(t

)}

(9)

Conclusively, the set of resources to be deactivated

is deﬁned as the relative complement of R

Sys

) in

∆

) and described by the following formula:

∆

) = R

Sys

) \ ∆

) (10)

Finally the new set of active resources after recon-

ﬁguration (R

Sys

)) is expressed as the addition of

resources ξ

) and the removal of the tasks ∆

)

from the old set of tasks established at t

. The formula

describing R

Sys

) is given as follows:

Sys

) = R

Sys

) ∪ ξ

) \ ∆

) (11)

Running example 4:

Continuing from the previous running example,

the added resources (ξ

)) and the removed

ones (∆

)) are given as follows:

) = {R

,τ

}

∆

) = {R

} Subsequently, the new

set of active resources after reconﬁguration

Sys

)) is expressed as follows:

Sys

) = R

Sys

) ∪ ξ

) \ ∆

) =

{τ

,τ

}

5 CONTRIBUTION RPCP/RM

We propose in this section to resolve the paper’s orig-

inal problems that we detailed in the case study. In

fact, the automatic reconﬁguration of tasks and/or re-

sources can lead the system to deadlocks or the pos-

sible violation of deadlines by new or old tasks. Ex-

plicitly, the deadline is violated when a corresponding

task has some work left when it reaches it. As for the

deadlock, it happens when a task holds resources that

another one is waiting for and inversely.This is prop-

erly explained in the following formula:

Problem :







∃τ

/τ

.W > τ

.D −t

∃τ

,τ

/τ

.Request(t

) ∩ τ

.Res(t

) 6=

∧τ

.Request(t

) ∩ τ

.Res(t

) 6=

(12)

As a consequence to the mentioned problems, the exe-

cution of the hardware processor is split into two vir-

tual processors in the purpose of pre-computing the

proposed optimizations when applying the reconﬁg-

uration at t

. One of the virtual processors continues

the normal execution of old tasks normally without in-

terruption while the other one computes the right set

of periods and priorities. The latter mentioned proce-

dure is decomposed in several sub-steps: the blocking

time minimization of the new and old tasks, response

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

time minimization, assuring feasibility without dead-

lock due to the addition of resources and meeting the

RM condition.

5.1 Virtual Processors

In order to guarantee the non-interruption of the exe-

cution of the system, spreading the physical processor

into two distinguished virtual processors, which are

time slots, was taken into consideration. The idea be-

hind this, is to gain in terms of computation without

having any time gaps during the execution of the old

tasks. In this study, two virtual processors are pro-

posed. The ﬁrst one, denoted as V P

takes the respon-

sibility of computing the new appropriate periods and

priorities to be assigned to both the old and new tasks

after reconﬁguration. The second one, V P

, executes

normally the old tasks by using the regular PCP. Fig-

ure 3 explains how the two virtual processors operate

in order to switch safely from a conﬁguration to an-

other without interrupting the current execution.

Figure 3: Roles of the virtual processors within the system.

The instant t

, like we mentioned before, corresponds

to when exactly the reconﬁguration request occurred,

when the computation ended and t

when V P

ends

the freeing of resources. In fact, V P

executes the old

tasks and it does not switch to the new conﬁguration

until V P

ﬁnishes its computation and reveals the new

assortment of priorities and periods related to each

task. The step that proceeds the switch from a conﬁg-

uration to another, consists on allowing the tasks that

hold some resources to ﬁnish their execution under

the previous conﬁguration. Let Newconf be the group

of tasks saved at t

to be used in the computation done

by V P

. It is formulated by using (7). However, at

, τ

Sys

) changes and represents the group of tasks

which did not ﬁnish their execution time when the re-

conﬁguration took place. It is therefore given by the

following formula:

Sys

) = {τ

∈ τ

Sys

)/τ

.S < t

∧ τ

.W (t

) 6= 0}

(13)

As a consequence, The group of resources R

Sys

)

within the actual system depends on the change that

occurred to τ

Sys

) as remarked in the formula (3).

Thus, the moment t

, previously described as when

V P

ended freeing the resources, is disposed by the

following formula:

= max(τ

/τ

∈ τ

Sys

)) (14)

The phase of computation to be realized by V P

, con-

sists on ﬁnding the right set of periods and priorities.

After this phase, the actual virtual processor VP

will

be able to run under the new conﬁguration. The exact

moment when the latter virtual processor starts ap-

plying the new conﬁguration is depicted as t

new

and

described as follows:

new

= max(t

) (15)

Running example 5:

Proceeding further in the example given in the

case study, the results obtained at t

, t

and

new

are explained in details. At t

, Newconf =

{τ

,τ

} and τ

Sys

) = {τ

}. At t

, V P

ﬁnishes the computation and the application of

the new periods and priorities of the task set

Newconf. At t

, τ

ﬁnishes executing R

. At t

new

Sys

new

) = Newconf.

5.2 Appropriate Set of Periods

At t

new

, V P

is able to run the new set of tasks re-

sulting from the computation done by V P

. In our

contribution, τ

Sys

new

), previously deﬁned in (7), is

described as the modiﬁcation of the priorities and pe-

riods that belong to the group of tasks Newconf gener-

ated from the reconﬁguration request. This modiﬁca-

tion that we propose, described in the formula (16), is

performed by the recursive function Ψ which is com-

puted in several steps.

Sys

new

) = Ψ(Newcon f ) (16)

Furthermore, in order to calculate the new temporal

conﬁgurations of tasks, some steps need to be fol-

lowed. the function Ψ is the composition of several

other sub-functions such that each of one corresponds

to a step of calculation.This is shown by the formula

(17).

Ψ = Ψ

◦ Ψ

(17)

In fact, to calculate the new system conﬁgura-

tion τ

Sys

new

), we need to compute at ﬁrst time,

(Newcon f ) which is in charge of ﬁnding the right

arrangement of priorities that ensures a minimum

blocking time. Then we apply the sub-function Ψ

the result of Ψ

(Newcon f ) which is responsible for

ﬁnding the right periods for which the response time

of each task is minimum. Ψ

is applied to the result of

: it is bound to ﬁnd the periods for which the dead-

line constraint is respected. And ﬁnally, Ψ

is applied

ReconfigurablePriorityCeilingProtocol-UnderRateMonotonicBasedReal-timeScheduling

to the result of Ψ

: it adjusts the obtained periods to

meet the condition of RMS. It is to mention, that these

recursive functions are not contradictory and that they

are applied to this conﬁguration without proposing

apposed values.

5.2.1 Ψ

: Minimum Blocking Time

For the purpose of identifying the minimum array of

blocking times related to the tasks, we use an algo-

rithm that reads through all the possible arrangements

of priorities that the tasks may have. Thereafter, it

spots the right set for which the blocking times are

at their minimum. The number of possibilities of

priorities that a vector of tasks can have, is based

on the same principle in combinatorics. For each

of these arrangement possibilities, the corresponding

array of blocking times is computed. Accordingly,

the comparison between the resulting vectors is per-

formed by the calculation of the Euclidean norm. As

a result, the proposed function Ψ

is deﬁned as a n-

tuple formed by pairs of priorities and tasks. Let {(

,τ

),..., (P

,τ

)} denoted as E

be the actual n-tuple

corresponding to the group of tasks Newconf and {(

,τ

),..., (P

,τ

)} denoted as E

be the resulting ar-

rangement of tasks. The deﬁnition of the function is

regarded by the following formula:

: E1 → E2

/∀(P

,τ

) ∈ E

∑

i=1

= min(

∑

k=1,(P

,τ

)∈E

)

(18)

Where [P

,..., P

] is the same as the vector of priorities

,..., P

] just in a different order of its elements. It

is important to retain that the priority with the least

index is the highest among all priorities.

Running example 6:

This example aims to ﬁnd the right set of priori-

ties that guarantee a minimum blocking time for

each task in Newcon f . The following table con-

tains the resulting minimum blocking time and

the corresponding new priority to each task.

Tasks Initial blocking times Minimum blocking times Old Priority new priority

0 6 P

12 12 P

15 14 P

17 0 P

15 15 P

The norm of the values of the initial blocking

times is 29,71. As for the one corresponding to

the Minimum blocking times, its value is 24,51.

5.2.2 Ψ

: Minimum Response Time

Once the ﬁrst step dealing with Ψ

is done we apply

its result to the function Ψ

. Attaining a speciﬁc set

of priorities, is only effective when it comes to ac-

quiring the appropriate values of periods. As matter

of fact, the next step consists on ﬁnding the right pe-

riods for which the response time of each task is at

its minimum. In this contribution, we can deﬁne the

minimum response time that a task can have (as long

as the priority of the latter is not the maximum) as the

sum of its blocking time, its execution time and the

execution times of the tasks that are more prioritized.

For each task τi, the minimum response time, denoted

as R

i,min

, is therefore given by the following formula:

i,min

(

+ B

i f P

= max(P

,...,P

)

+ B

∑

else

(19)

The obtained response times allow the possibility of

deﬁning the boundaries of the period. In fact, the gen-

eralization consists on limiting the periods of all the

tasks (except the one with the lowest priority) with

the maximum of response times among the least pri-

oritized ones. Referring to the previous analysis, let

prior

be the set of tasks except the least prioritized

(respecting the order set by Ψ

). The function Ψ

replaces the values of periods of tasks belonging to

prior

with the maximum of response times of the pri-

oritized tasks incremented by one. This is given by

the following formula :

: τ

.T → max(R

) + 1/∀k : P

< P

(20)

Running example 7:

After assigning new priorities to the given tasks

mentioned in the case study, the process of ﬁnd-

ing the minimum possible periods starts.

Tasks Minimum response times new periods

11 23

22 23

19 45

22 0

44 23

Since τ

has the lowest priority, no period value

is affected to it yet.

5.2.3 Ψ

: Feasibility Test

Once the application of Ψ

is done, he results of the

previous steps are applied to Ψ

. Going further in

ﬁnding the periods, the respect of the constraint of

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

feasibility should be promulgated. In fact, bearing in

mind the feasibility condition imposed by the system

can allow limiting the period. So far, let Boundary

be the inferior limit of the resulting period.

Boundary



+ R

i f τ

is the least prioritized task

max(A

+ R

,τ

.T )) i f not

(21)

Thus, the deﬁnition of our submitted function Ψ

is:

: ∀τ

: τ

.T → Boundary

+ 1 (22)

Running example 8:

Continuing in the example of the case study, the

process of ﬁnding the possible periods that per-

mit the respect of the feasibility continues.

Tasks Starting times (A) A+R Periods obtained from Ψ

new Periods

3 14 23 24

1 23 23 24

5 24 45 46

2 28 0 29

4 48 23 49

The new periods obviously correspond to the

maximum between the sum of A and R, and the

periods previously obtained from Ψ

5.2.4 Ψ

: RM Condition Test

Once Ψ

is well executed,we apply its result to Ψ

Basically, the procedure is done by incrementing the

values of the periods until fulﬁlling the RM condition.

Therefore, we make a place for a system that min-

imizes the response time, allows the feasibility and

respects the condition imposed by the Rate Mono-

tonic Scheduling (RMS). Hence, the function Ψ

proposed to guarantee the respect of the latter condi-

tion which is expressed by the following formula:

: ∀τ

: τ

.T → τ

.T /

∑

j=1

C j

T j

≤ n ∗ (2

− 1) (23)

Running example 9:

Finally, the following table describes the list of

periods obtained after running a loop of incre-

mentation that allows to obtain the required peri-

ods of tasks that respect the RM condition.

Tasks Execution times new Periods

5 32

5 31

5 53

7 36

7 56

It is to mention that the obtained value of τ

and τ

is the same in this example. But, since

is less prioritized than τ

, we incremented it

in order to point out the distinct priorities. The

value of

∑

j=1

C j

T j

is around 73% which is less than

74,35% (the value of 5 ∗ (2

− 1)).

5.2.5 Solution

The global function Ψ allowing the correct reconﬁg-

uration of the real-time system (applied to both the

old and new tasks) is composed of Ψ

, Ψ

and

. It permits to have a group of tasks that imple-

ment the system while satisfying the following items:

(i) avoiding the deadlock anomaly, (ii) respecting the

RM condition as well as minimizing (iii) the response

time of the tasks and (iv) their blocking times. Sub-

sequently, the resulting group of tasks that implement

the system are free from the problems mentioned in

(12) and characterized as follow :

Solution :











(VirtualProcessors)∀τ

,∀τ

/τ

6= τ

∧τ

.Request(t) ∩ τ

.Rest(t) =

0(i)

(Ψ

) ∀τ

/τ

.B = Minimum(τ

.B)(iv)

(Ψ

) ∀τ

/τ

.R = Minimum(τ

.R)(iii)

(Ψ

) ∀τ

/τ

.W < τ

.D −t

(ii)

(Ψ

) ∀τ

∑

i=1

≤ n ∗ (2

− 1)(ii)

(24)

6 SIMULATION

Deﬁning the procedures mentioned in the formaliza-

tion in an algorithmic way consists on running two

distinguished threads Algorithm1. The ﬁrst one exe-

cutes the actually active tasks with regular PCP. The

second computes the blocking times and right ar-

rangements of priorities , then starts the procedure of

calculating the response times and the periods. Fi-

nally it checks the feasibility and the RM Condition in

order to deliver the new information to the ﬁrst thread.

For the purpose of simulating the RPCP and showing

its contribution compared to random behavior towards

reconﬁguration, we developed a tool at LISI Labora-

tory of INSAT Institute (Figure 4) that allows the user

to ﬁll in with the desired tasks parameters. Afterward,

it is possible to ﬁll with the parameters of the tasks

that had been added to the system after the reconﬁgu-

ration through the interface presented in Figure 5.

ReconfigurablePriorityCeilingProtocol-UnderRateMonotonicBasedReal-timeScheduling

Algorithm 1 : Proposed response to Reconﬁguration re-

quest.

Data: New Reconﬁguration Request

Tau Sys1 ← tasks holding resources

NewCon f ← tasks resulting f rom recon f iguration

while VP1.end = False And VP2.end = False do

Tau Sys2 ← V P1.Execute(NewCon f )

VP2.Execute(Tau Sys1)

end

VP2.Execute(Tau Sys2)

Figure 4: Initial tasks parameters interface.

The testing of the behavior of the system before and

after the application of RPCP is pin pointed through

the interface depicted in Figure 6. It is possible to no-

tice that a blocking occurred when using the random

reaction to the reconﬁguration and how this problem

was solved by using RPCP and the system continues

its execution smoothly. The response time is then

computed for each of the tasks and an average re-

sponse time for both before and after the application

of the RPCP (Figure 7). We show the gain in terms

of response time due to RPCP. Through the test done

over the case study, the improvement is noticeably ob-

vious. In fact the blocking time is managed to get

reduced to almost 80%. Consequently, the response

time decreased to 75% compared to the initial proce-

dures.

We note ﬁnally that no one in the related works

treated the problem of reconﬁgurable resources while

meeting deadline constraints for reconﬁgurable tasks.

Figure 5: Reconﬁguration tasks parameters interface.

Figure 6: Execution before and after RPCP.

This tool is original and the ﬁrst to treat this original

problem.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

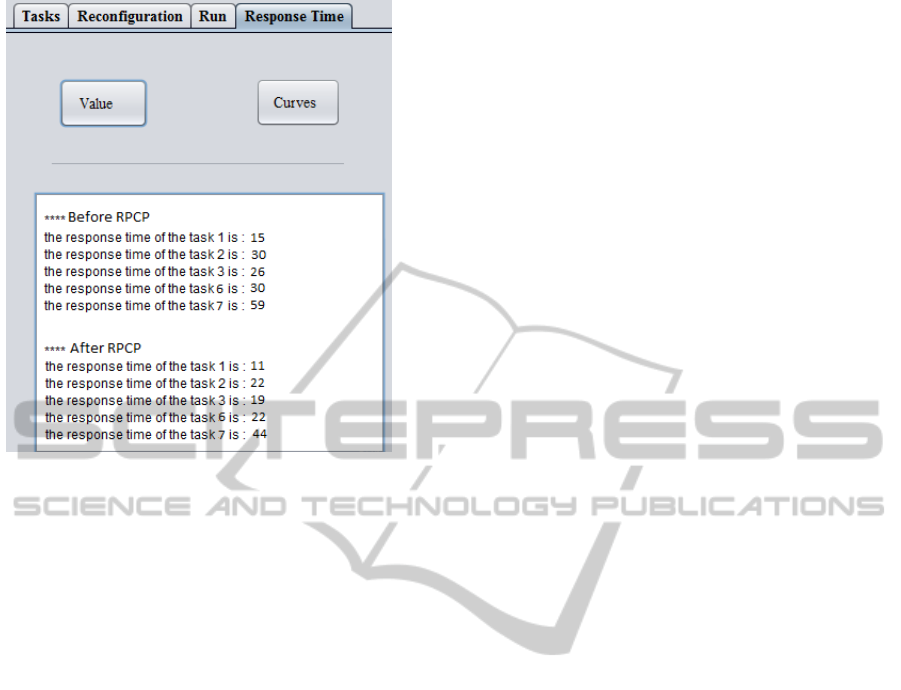
Figure 7: Response Time details.

7 CONCLUSION

In this paper, we introduce RPCP as a protocol that

solves well-deﬁned real-time problems due to random

reaction to reconﬁguration. In fact, the power within

this protocol lies on two different bases. The ﬁrst one,

corresponds to the choice of well-based scheduling

methods and their ability to solve problems and opti-

mize the parameters of the system. Surely, the use of

a solid scheduling algorithm such as Rate Monotonic

and an efﬁcient protocol like Priority Ceiling Proto-

col reﬂects an important beneﬁt to conclude from the

proposed solution. Since the ﬁrst one is known for its

utility and optimality in the industrial ﬁeld and the

second one is able to prevent deadlocks as well as

chained blocking. The second advantage of the pro-

posed protocol RPCP, is its ability to ﬁx the dead-

lock problems and to prevent exceeding the dead-

lines. Moreover, this protocol works on minimizing

the blocking and the response times by changing the

priorities of the tasks, leading to an optimal system

that runs effectively. We plan in the future to apply

this protocol to real complex case studies in order to

evaluate the contributions of the current paper.

REFERENCES

Brennan, R. W., Fletcher, M., and Norrie, D. H. (2002). An

agent-based approach to reconﬁguration of real-time

distributed control systems. Robotics and Automation,

IEEE Transactions on, 18(4):444–451.

Chen, M.-I. and Lin, K.-J. (1991). A priority ceiling proto-

col for multiple-instance resources. In Real-Time Sys-

tems Symposium, 1991. Proceedings., Twelfth, pages

140–149. IEEE.

Colnaric, M. and Verber, D. (2007). Distributed Embed-

ded Control Systems: Improving Dependability with

Coherent Design. Springer.

Farcas, E. (2006). Scheduling multi-mode real-time dis-

tributed components. PhD thesis, PhD thesis, Depart-

ment of Computer Sciences, University of Salzburg.

Gharbi, A., Gharsellaoui, H., Khalgui, M., and Valentini, A.

(2011). Safety reconﬁguration of embedded control

systems.

Gharbi, A., Khalgui, M., and Ben Ahmed, S. (2013).

The embedded control system through real-time task.

In Modeling, Simulation and Applied Optimization

(ICMSAO), 2013 5th International Conference on,

pages 1–8. IEEE.

Kalinsky, D. (2003). Basic concepts of real-time operating

systems. LinuxDevices magazine, Nov.

Khalgui, M., Mosbahi, O., Li, Z., and Hanisch, H.-M.

(2011). Reconﬁguration of distributed embedded-

control systems. Mechatronics, IEEE/ASME Trans-

actions on, 16(4):684–694.

Lee, I., Leung, J. Y., and Son, S. H. (2007). Handbook of

real-time and embedded systems. CRC Press.

Lehoczky, J., Sha, L., and Ding, Y. (1989). The rate mono-

tonic scheduling algorithm: Exact characterization

and average case behavior. In Real Time Systems Sym-

posium, 1989., Proceedings., pages 166–171. IEEE.

Lipari, G. and Bini, E. (2003). Resource partitioning among

real-time applications. In Real-Time Systems, 2003.

Proceedings. 15th Euromicro Conference on, pages

151–158. IEEE.

Liu, C. L. and Layland, J. W. (1973). Scheduling algo-

rithms for multiprogramming in a hard-real-time en-

vironment. Journal of the ACM (JACM), 20(1):46–61.

Liu, F., Narayanan, A., and Bai, Q. (2000). Real-time sys-

tems. Citeseer.

Mok, A. K., Feng, X., and Chen, D. (2001). Resource par-

tition for real-time systems. In Real-Time Technology

and Applications Symposium, 2001. Proceedings. Sev-

enth IEEE, pages 75–84. IEEE.

Pedro, P. and Burns, A. (1998). Schedulability analysis

for mode changes in ﬂexible real-time systems. In

Real-Time Systems, 1998. Proceedings. 10th Euromi-

cro Workshop on, pages 172–179. IEEE.

Real, J. and Crespo, A. (2004). Mode change protocols

for real-time systems: A survey and a new proposal.

Real-time systems, 26(2):161–197.

Sha, L., Rajkumar, R., Lehoczky, J., and Ramamritham,

K. (1989). Mode change protocols for priority-driven

preemptive scheduling. Real-Time Systems, 1(3):243–

264.

Sha, L., Rajkumar, R., and Lehoczky, J. P. (1990). Prior-

ity inheritance protocols: An approach to real-time

synchronization. IEEE Transactions on computers,

39(9):1175–1185.

ReconfigurablePriorityCeilingProtocol-UnderRateMonotonicBasedReal-timeScheduling

Singhoff, F., Legrand, J., Nana, L., and Marc

e, L. (2004).

Cheddar: a ﬂexible real time scheduling framework.

In ACM SIGAda Ada Letters, volume 24, pages 1–8.

ACM.

Stankovic, J. A. (1996). Real-time and embedded systems.

ACM Computing Surveys (CSUR), 28(1):205–208.

Stewart, D. B., Volpe, R. A., and Khosla, P. K. (1997). De-

sign of dynamically reconﬁgurable real-time software

using port-based objects. Software Engineering, IEEE

Transactions on, 23(12):759–776.

Stoimenov, N., Perathoner, S., and Thiele, L. (2009). Re-

liable mode changes in real-time systems with ﬁxed

priority or edf scheduling. In proceedings of the Con-

ference on Design, Automation and Test in Europe,

pages 99–104. European Design and Automation As-

sociation.

Tindell, K. and Alonso, A. (1996). A very simple proto-

col for mode changes in priority preemptive systems.

Universidad Polit

ecnica de Madrid, Tech. Rep.

Tindell, K. W., Burns, A., and Wellings, A. J. (1992). Mode

changes in priority preemptively scheduled systems.

In Real-Time Systems Symposium, 1992, pages 100–

109. IEEE.

Tokuda, H., Nakajima, T., and Rao, P. (1990). Real-time

mach: Towards a predictable real-time system. In

USENIX Mach Symposium, pages 73–82.

Wang, J.-C., Chiang, H.-D., and Darling, G. R. (1995).

An efﬁcient algorithm for real-time network recon-

ﬁguration in large scale unbalanced distribution sys-

tems. In Power Industry Computer Application Con-

ference, 1995. Conference Proceedings., 1995 IEEE,

pages 510–516. IEEE.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics