
Research on Routing and Wavelength/Subcarrier Assignment
Algorithm based on Layered-Graph Model in Optical Satellite
Networks
Yuanyue Guo, Dongjin Wang and Falin Liu
Key Laboratory of Electromagnetic Space Information, Chinese Academy of Science,
University of Science and Technology of China, Hefei, China
Keywords: Optical Satellite Networks, Two-Level Switching, Subcarrier Layered-Graph, Routing and
Wavelength/Subcarrier Assignment.
Abstract: In optical satellite networks with multi-wavelengths and multi-subcarriers, two-level switching mode
replace single wavelength switching, achieving better flexibility and network performance with its
disadvantages of more complex routing and network resource allocation. Based on subcarrier layered-graph
(SL-G), a novel dynamic routing and wavelength/subcarrier assignment (RWSA) algorithm is proposed to
find the shortest path with limited costs in the corresponding layered-graph. By defining different edge cost
functions in SL-G, centralized resource allocation strategy and decentralized resource allocation strategy in
dynamic RWSA are analysed for optical satellite networks with different types of constellations. Simulation
results demonstrate that, no matter whether optical satellite networks has single constellation with uniform
wavelength distribution or hybrid constellations with non-uniform wavelength distribution, the proposed
RWSA algorithms are superior to traditional routing and wavelength assignment algorithms with lower
network blocking probability.
1 INTRODUCTION
Optical satellite networks have been a research
hotspot in the satellite communication field (Sodnik
et al, 2010). With the performance improvement of
optical inter-satellite laser link (OISL), it is a very
important development direction to build an optical
satellite networks by wavelength division
multiplexing (WDM) and wavelength routing
technology for the future broadband, high-capacity
space communications (Yang et al, 2010; Yang et al,
2009). In order to establish OISLs, the required
wavelength number has to grow nearly at the speed
of square law while satellite nodes increases, which
limited the scale of optical satellite networks
severely (Baroni and Bayvel, 1997; Tan et al, 2010).
Considering microwave links are used between
satellites and ground, a scheme of optical satellite
networks with two-layered wavelength/subcarrier
routing (TWSR-OSN) has been proposed (Guo et al,
2003) to resolve its serious insufficient of
wavelength resources, which keeps its advantage of
wavelength routing and its better flexibility.
In optical satellite networks, each OISL can have
multiple wavelengths; and satellite nodes can
perform switching of data streams by wavelength-
routing algorithms. The issue is how to use fewer
network resources, such as nodes, ports,
wavelengths and so on, to obtain the most network
throughput with minimum time delay and least
blocking probability, so it becomes very critical to
adopt a better routing and wavelength assignment
algorithm (Poo et al, 2006; Cardoso et al, 2010).
In TWSR-OSN, wavelength and subcarrier are
expensive network resources. When a subcarrier
channel in a wavelength is established, two-layered
routing is helpful to improve the network
performance, so it is necessary to study its dynamic
RWSA algorithm. But its logical hierarchy with
double granularity switching is more complicated,
some switching belongs to subcarrier layer while the
others maybe belong to wavelength layer[6].
Distinguished to optical terrestrial networks with
WDM, most optical satellite networks consist of
different satellite constellations with its unique
attributes and features, such as low earth orbit (LEO),
medium earth orbit (MEO), geosychronons earth
69
Guo Y., Wang D. and Liu F..
Research on Routing and Wavelength/Subcarrier Assignment Algorithm Based on Layered-graph Model in Optical Satellite Networks.
DOI: 10.5220/0005061700690076
In Proceedings of the 5th International Conference on Optical Communication Systems (OPTICS-2014), pages 69-76
ISBN: 978-989-758-044-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

orbit (GEO), where its OISL distributions are
asymmetry obviously. Therefore WRSA problem
has to be studied respectively in two cases that
OISLs have uniform or non-uniform wavelength
distributions.
Based on a novel subcarrier layered-graph,
dynamic RSWA algorithm is presented with
centralized allocation strategy and decentralized
allocation strategy on the network resources, In
order to make the scheme more general, two types of
TWSR-OSN are analyzed: one has OISLs with
uniformly distributed wavelengths and the other has
OISLs with non-uniformly distributed wavelengths.
The remaining sections are organized as follows.
In section 2, two-layer switching structure is
analyzed, and SL-G model is set up in section 3. In
section 4, based on SL-G model, RSWA algorithms
are proposed with two strategies for different types
of TWSR-OSN. Section 5 shows the simulation
results of RWSA algorithms. Section 6 concludes
the work.
2 TWO-SWITCHING
STRUCTURE & WORKING
MECHANISM
Due to two relatively independent logical sub-layers
of wavelength and subcarrier, TWSR-OSN can
perform unique two-level switching, therefore
satellite node’s switching structure is a kind of
hybrid granularity exchanging of wavelength and
subcarrier. Its working mechanism is that each
satellite node can demultiplex the OISL into a single
wavelength, or a single subcarrier channel. Although
its switching structure become complicated with
higher cost, the traffic load can realize two-level
switching by adding and dropping in wavelength
layer or subcarrier layer, based on routing status in
TWSR-OSN.
Figure 1 shows two-level switching structure.
For the incoming wavelength link and subcarrier
channel, wavelength switching matrix and subcarrier
switching matrix act as a selector and a space
division switch so that input traffic can select
different switching granularity of wavelength or
subcarrier according to the switching matrix
configuration. Of course, switching matrix can
switch wavelength and subcarrier simultaneously, as
well as only wavelength.
Figure 1: Two-level switching structure.
Because both of the same wavelengths cannot
converge into one OISL at the same time while both
of the same subcarriers cannot converge into one
wavelength, both wavelength continuity constraints
and subcarrier continuity constraints have to be met
simultaneously. In Figure 1, wavelength switching
matrix can only exchange the same wavelength from
different OISLs, while subcarrier switching matrix
can only exchange the same subcarrier from
different wavelengths in different OISLs.
3 SL-G MODEL
According to subcarrier continuity constraints, each
available network path in multiple OISLs must be
assigned the same subcarrier, namely, in the same
subcarrier plane, each satellite node is divided into
multiple virtual nodes with different sub-layers,
where each sub-layer indicates only one wavelength
in OISL, therefore, two-level switching structure can
perform cross-connect between these virtual nodes,
and each edge between virtual nodes is determined
uniquely by one subcarrier and one wavelength.
Given a TWSR-OSN topology
()G N,L,W,S
,
where
N
represents physical satellite node sets, and
L
is all directed link sets among satellite nodes, for
any OISL,
a,b
l
is a link between node
a
and node
b
and
a,b
lL
;
a,b
W
is its available wavelengths sets of
a,b
l
, so all wavelength sets
W
a,b
W
;
S
is a
subcarrier sets
, , .....
K
123
S
SSS S
in each wavelength
channel. If
W
W
is a wavelength sets which are used
for wavelength switching, and
S
W
is a wavelength
sets that are used for subcarrier switching, then
WS
WW W.
The subcarrier layered-graph (
SL
-
G)
is a directed
graph. For OISLs in a given TWSR-OSN with
uniformly-distributed resources, each link
a,b
l
has the
same wavelength sets
W
, and each wavelength has
the same subcarrier sets
S
, so its
SL
-
G
(
V
,
E
)
can be
obtained by two steps.
Firstly, a subcarrier sub-graph
can be made by
the following steps:
OPTICS2014-InternationalConferenceonOpticalCommunicationSystems
70

1)Each node
a N
is replicated
|
|
W
times to
get a virtual nodes sets
s,1 s,2 s,w s,
|
W
|
aa a a
Vv,v,v v
, where
WS
VV V,
W
V
and
S
V
are two kinds of virtual
node sets corresponding to wavelength switching
ports and subcarrier switching ports respectively.
For any virtual node
s
,w
a
v
, when
W
wW
,
s
,w W
a
vV
,
similarly, when
S
wW
,
s,w S
a
vV
.
2)For an available link
a,b
l
, two virtual nodes
s
,i s,1 s,2 s,|W |
aaa a
vv,v,v
and
s, j s,1 s,2 s,|W |
bbb b
vv,v,v
can
be connected by two edges
s
,i, j
a,b
e
and
s
,j,i
b,a
e
in opposite
directions, where
s,i, j s, j,i
a,b b,a
e, e E
∈
and
E
is defined as an
all edge sets, and one edge corresponds to one
possible path between node
a
and
b
in
SL
-
G
(
V
,
E
)
.
3) In order to accomplish the adding/dropping
requests in subcarrier layer, two virtual nodes have
to be added for each node in
(, )
S
L-G V E
: source
node
s,o
a
v
denote a producing service entity of access
node
a
, and destination node
s
,d
a
v
represents an
absorbing service entity of dropping node
a
.
Meanwhile two directed edges have to been added
from source node
s
,o
a
v
to virtual nodes
12 |S|
s,w s,w s,
|
w
aa a
v,v, v
and from virtual nodes
12 |S|
s,w s,w s,
|
w
aa a
v,v, v
to destination node
s
,d
a
v
, and
,,
S12
|
S
|
Wwww
, where the costs of the two directed
edges are set to 0.
Secondly
,
by duplicating above sub-graph
||
S
times,
||
S
sub-graphs can be achieved with
||
S
different subcarrier planes, which make up a whole
SL
-
G
(
V
,
E
)
shown in Figure 2, where every
subcarrier plane is equivalent with each other.
Figure 2: SL-G Model.
Assuming that each OISL is bidirectional in
SL
-
G
(
V
,
E
)
, a subcarrier path corresponds to a pair of
edges in opposite direction. Figure 2 shows a
subcarrier path in subcarrier plane
s
2
via a route
2,1 1,5
ll
from node
2i
2
s
,w
V
to node
2j
5
s,w
V
, which
corresponds to a pair of directed edges
2,i, j
2,1
e
,
2,i, j
1,5
e
and
2, j,i
5,1
e
,
2, j,i
1,2
e
, and subcarrier
s
2
and wavelengths
ij
w,w W
are assigned to them. Consequently, dynamic
RWSA problem in optical satellite networks can be
solved simultaneously by the proposed
SL
-
G
(
V
,
E
)
model.
Obviously, subcarrier continuity constraint in
SL
-
G
(
V
,
E
)
can be ensured by allocating different
subcarrier channels in the different subcarrier planes
correspondingly, then RWSA problem in TWSR-
OSN is simplified to find a path with minimum cost
from source node
s
,o
a
v
to destination node
s
,d
b
v
, which
will provide a desired routing in a determined
subcarrier plane.
It is noticed that the edges of subcarrier channels
in all subcarrier planes are independent in
SL
-
G
(
V
,
E
)
, however, the edges of wavelength channels
between virtual nodes in different subcarrier planes
are dependent. Once a wavelength is used out in one
subcarrier plane, the cost of all edges which the
wavelength passes should be set to infinity,
meanwhile, the costs of related edges with the same
wavelength in else subcarrier planes are also set to
infinity.
4 DYNAMIC RWSA ALGORITHM
BASED ON SL-G MODEL
4.1 Definition of Edge Costs
In
SL-G
model, dynamic RSWA problem is
equivalent to find a minimum cost path in TWSR-
OSN, which should make full use of network
resources, including wavelengths and subcarriers,
and meet the service requests of network connection
of subcarrier channels as far as possible.
In TWSR-OSN, the cost of each edge in
SL-G
is
a scalar, which is much more complex and affected
by many factors, including inter-satellite distances,
QoS, different constellations and switching levels
etc. Different definitions of each edge cost will lead
to two different resource allocation strategies and the
corresponding RSWA algorithms. The definition of
different edges and its cost functions based on
different strategies are followed.
For edge
m,i, j
a,b
e
, subscript
a
is source node number
and
b
is terminal node number in satellite networks,
m
indicates the subcarrier plane which this edge
belongs to in the
SL-G
,
i
and
j
represent the
wavelength number of virtual nodes;
W
T
is
wavelength sets and
S
T
indicates subcarrier channel
sets.
ResearchonRoutingandWavelength/SubcarrierAssignmentAlgorithmBasedonLayered-graphModelinOpticalSatellite
Networks
71

4.1.1 Centralized Strategy
When
W
iW
and
W
j
W
,
m,i, j W
a,b
eT
12
,,
,1 2
,,
,
,,
,
,,
,
,
,
,,,,
()
, ,,,,
mf f
ab
si f
ab
mi j
ab
sf j
ab
W
ab
if flowis assignedtoe f i or f j
or to e f W f j s S s m
Ce
or to e f W f i s S s m
Cotherwise
(1)
When
S
iW
or
S
j
W
,
m,i, j S
a,b
eT
12
,,
,1 2
,,
,
,,
,
,,
,
,
,
,, ,,
()
,,,,
mf f
ab
si f W W
ab
mi j
ab
sf j W W
ab
S
ab
if flowis assigned toe f i or f j
or to e i W f W s S s m
Ce
or to e j W f W s S s m
Cotherwise
(2)
The constraint conditions are:
,,
,
()0, , , , ,
mi j
ab
Ce m S i W j W a N b N
(3)
Where
W
a,b
C
and
S
a,b
C
are the initial cost constants
of wavelength and subcarrier channel from node
a
to
node
b
respectively. It is noticed that if each
subcarrier plane is equivalent completely, cost
function of different edges corresponding to the
same link is exactly the same.
After the establishment of a new subcarrier
channel, if there are idle subcarrier channels in the
edge, its cost is
m,i, j
a,b
C(e )
, otherwise, its cost is set to
infinity. Concentrated strategy encourage optical
path to use least network source by setting up
subcarrier channels in less edges on the least
subcarrier planes as far as possible, so more network
resources can be reserved to meet much more
service requests of subcarrier channels.
4.1.2 Decentralized Strategy
Under the decentralized strategy, the edge cost of
m,i,
j
a,b
e
is given as follows:
When
W
iW
and
W
j
W
,
m,i,j W
a,b
eT
12
,,
,1 2
,,
,
,,
,,
,
,
,,
,, ,
,
,,,,
()
, ,,, ,
()
WW
mf f
ab
si f
ab
mi j
sf j
ab
ab
si j
ab ab ab
sS
if flowis assigned to e f i or f
j
or to e f W f j s S s m
Ce
or to e f W f i s S s m
COeotherwise
(4)
When
S
iW
or
S
j
W
,
m,i, j S
a,b
eT
12
,,
,1 2
,,
,
,,
,,
,
,
,,
,, ,
,
,, ,,
()
,,,,
()
S
mf f
ab
si f W W
ab
mi j
sf j W W
ab
ab
Ssij
ab ab ab
sS
if flowis assigned to e f i or f j
or to e i W f W s S s m
Ce
or to e j W f W s S s m
COeotherwise
(5)
Where
W
a,b
δ
is a coefficients used to adjust the
changing trend of edge cost of a wavelength as its
occupied subcarrier number changes, and
S
a,b
δ
is a
coefficients used to adjust the changing trend of
edge cost of a subcarrier channel as the occupied
subcarrier number changes in the same wavelength.
Both of them can be configured according to the
network conditions.
,,
,
()
s
ij
ab
eO
is used to judge if its edge cost of
s
,i, j
a,b
e
is
infinity, which is defined as follows:
,,
,
,,
,
1()
()
0otherwise
si j
ab
si j
ab
if C e
Oe
(6)
Because of its action of
W
δ
and
S
δ
, no matter
which kind of the shortest path algorithm is adopted,
decentralized strategy will promote the existing calls
to route in wavelength channel and subcarrier plane
with lower utilization, so that all traffic loads will be
distributed uniformly in all wavelength channels and
all subcarrier planes as far as possible.
By setting different
WS
a,b a,b a,b
CCorC
, two
strategies can derive different RSWA algorithms
suitable for different types of optical satellite
networks.
A) TWSR-OSN with uniform wavelength
distribution and different link costs
Set a link cost matrix
,| |
{}
ab
BC
N| |N
BC
, where
,ab
B
C
represents its basic cost of
a,b
s,i,
j
e
. If
a,b
s,i,
j
e
doesn't
exist,
,ab
BC
. For such a network, Let:
,,
,,
ab ab
ab ab
CBC
B
C
(7)
Obviously, the network with uniformly
distributed wavelengths and the same link costs is
just a special case when
a,b
C
=
a,b
δ
=1.
B) TWSR-OSN with non-uniform wavelength
distribution and the same link costs.
Matrix
,||||
{| |}
ab N N
W
WL
describes the wavelength
number distribution among OISLs,
LCM
(
WL
)
represents the least common multiple of all non-zero
element in matrix. For such a network, Let:
,,
,,
()/| |
()/| |
ab ab
ab ab
CLCMWLW
LCM WL W
(8)
OPTICS2014-InternationalConferenceonOpticalCommunicationSystems
72

In above formula, the less wavelength number an
OISL has, the bigger its corresponding
a,b
C
and
a,b
δ
are.
C) TWSR-OSN with non-uniform wavelength
distribution and different link costs.
For such a network, two types of definition of
a,b
C
and
a,b
δ
are given below.
,,,
,,,
()/| |
()/| |
ab ab ab
ab ab ab
CMCMWLWBC
M
CM WL W BC
(9)
,,
,,
()/| |
ab ab
ab ab
CBC
MCM WL W
(10)
If a calling request from node
a
to node
b
arrives,
let
a,b
P
represents all possible access path sets from
o
a
v
to
d
b
v
. If the edge
s
,i,
j
a,b
e
exists in a path
p
(
a,b
pP
),
let indicating function
s,i, j
a,b
x(
p
,e )= 1
, otherwise, let
s,i, j
a,b
x(p,e ) = 0
. If an new calling is established in path
p
, let indicating function
1y(p)
, otherwise, let
y
(
p
)=0
.
The minimum cost function
C(p)
of path
p
can
be expressed as:
,,
,
,
,, ,,
,,
() min{ ( ) (, ) ()}
si j
ab
ab
si j si j
ab ab
sSpP
eE
Cp ce xpe yp
(11)
The following condition must be met.
,
() 1
ab
pP
yp
(12)
For
ab
p
P
,
(){0,1}
s,i, j
a,b
xp,e
and
{0,1}
y(p)
.
Considering edge costs from source node
o
a
v
,
destination node
d
b
v
to its own virtual nodes has been
set to 0, formula (11) includes all edge sets
E
in
SL-
G
.
In summary, dynamic RSWA problem in
TWSR-OSN can be resolved by the shortest path
algorithm based on SL-G. If the shortest path with a
limited cost can be found from
o
a
v
to
d
b
v
in
corresponding
SL-G
, the calling request will be
accepted, otherwise, it will be rejected.
4.2 RWSA Algorithm Based on SL-G
By the shortest path algorithms, such as Dijkstra
algorithm, according to decentralized strategy and
centralized strategy, the dynamic RWSA based on
SL-G
can be performed by the following steps.
Step 1
: Convert a given TWSR-OSN with
G
(
N
,
L
,
W
,
S
) into
SL-G(V,E)
. According to different
types of satellite networks, proper
a,b
C
and
a,b
δ
is
defined by formula (7) to formula (10), and taken
into formula (1) and (2) or formula (4) and (5) based
on concentrated strategy or decentralized strategy ,
then initial cost of each edge
s
,i, j
a,b
e
can be achieved.
Step 2
: Waiting for the input calling. If a request
for subcarrier channel connection arrives, turn to
Step 3; if a request for releasing a connection
arrives, turn to Step 4.
Step 3
: According to the pair of nodes requested
by the input calling, the corresponding source node
and destination node
a
o
v
and
b
d
v
, as well as its edges
and its edge costs, are added into
SL-G
. By the
shortest path algorithm Dijkstra, search for the
shortest path
p
from
a
o
v
to
b
d
v
.
(1) If the shortest path cost
C
(p) is infinity, reject
the calling request, then turn to Step 2.
(2) If
C
(p) is limited, accept the request, and map
the shortest path
p
into the corresponding subcarrier
plane and wavelength channel in
SL-G
:
a) Map the distribution of all virtual nodes and
directed edges along the shortest path
p
into the
nodes and links in the physical optical satellite
networks, then a routing of the subcarrier path can
be obtained;
b) If the shortest path
p
passes through the k-th
subcarrier plane, assign subcarrier channel
s
k
to it;
c) According to the formula (1) and (2) or
formula (4) and (5), refresh the edge costs of related
links that the shortest path
p
passes through. Because
p
is a bidirectional path, edge cost functions of
s
,i, j
a,b
e
and
s
,j,i
b,a
e
must be refreshed at the same time, turn to
Step 2;
Step 4
: According to the formula (1) and (2) or
formula (4) and (5), refresh the edge costs of related
links that the subcarrier path passes through.
Step 5
: Release subcarrier path, turn to Step 2.
Considering the complexity of RSWA algorithm,
the influence of
a
o
v
and
b
d
v
and its edges connecting
to SL-G are ignored. The complexity of Step l is
proportional to the edge number of |E|, while the
complexity of Step 4 is nearly proportional to the
network diameter. Therefore the complexity of
dynamic RSWA algorithm is mainly determined by
the complexity of the shortest path algorithm
adopted in Step 3. If the shortest path algorithm with
the highest speed, such as Dijsktra algorithm, is
adopted, its complexity is
222
(| |) (| || |)OV O N S
.
5 SIMULATION RESULTS
Based on
S
L-G
model, numerical simulation will
be performed to compare the performance of two
RWSA algorithms in different types of TWSR-OSN:
one is denoted as RWSA-C derived from centralized
ResearchonRoutingandWavelength/SubcarrierAssignmentAlgorithmBasedonLayered-graphModelinOpticalSatellite
Networks
73
strategy while the other is named as RWSA-D
derived from decentralized strategy.
In simulations, two types of network topology
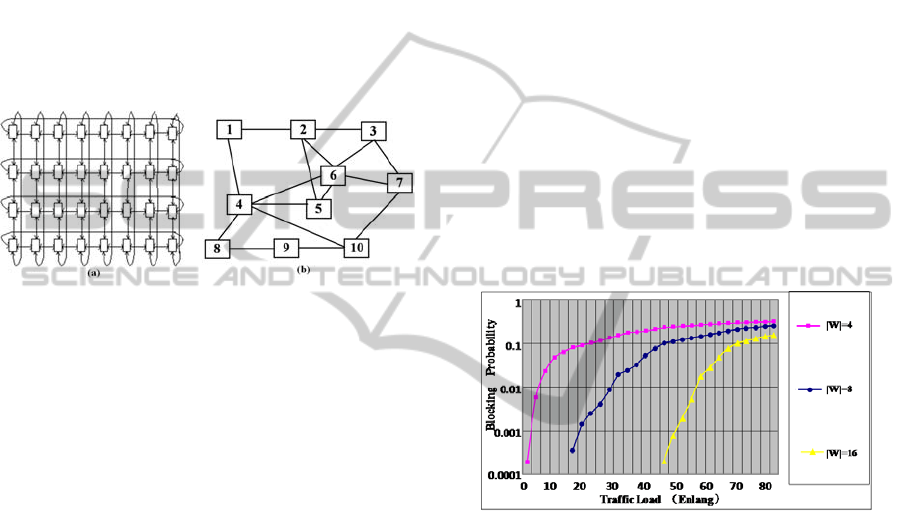
are used. As shown in Figure 3(a), a regular ring-
lattice topology represents TWSR-OSN with a
single constellation (such as LEO), which consists of
4 orbits with 8 satellites at each orbit, where each
satellite node has OISLs with four adjacent satellite
nodes at the same orbit and at the adjacent orbit,
meaning the whole network has 32 nodes and 64
OISLs. Figure 3(b) depicts an irregular network
topology, representing optical satellite networks
with hybrid constellations of LEO and MEO etc,
which has 10 nodes and16 OISLs.
Figure 3: (a) Regular network topology, (b) Irregular
network topology.
Assuming that requests for subcarrier channels
arrive randomly in Poisson Process with the network
arrival rate
, traffic intensity among all satellite
node pairs is distributed uniformly, while multiple
subcarrier paths between a pair of nodes are
permitted. After subcarrier paths are set up, its
services time depends on negative exponential
distribution with a mean value of
. The average
service time in TWSR-OSN is set to an unit time, so
it total network load is
. Once a subcarrier
channel connection request is rejected, it is
discarded immediately without a waiting queue
scheduling mode. In order to ensure the network into
a stable running status, 1
×
10
6
connection requests
are generated.
For comparison with the proposed RWSA
algorithm, two routing and wavelength assignment
algorithms are employed, including fixed routing
and First-Fit wavelength assignment algorithm
(FR/FF), fixed alternate routing and random
wavelength assignment algorithm (AR2) which
determines two alternate routes for each pair of
nodes by its basic costs.
A: TWSR-OSN with uniform wavelength
distribution and the same link costs
In TWSR-OSN with uniform wavelength
distribution and the same link costs, wavelength
number at each OISL is set to
||||
ij
W W
. For
simplicity, the basic cost
a,b
C
and
a,b
δ
of each edge in
any link
a,b
lL
in
S
L-G
are all set to 1.
Based on the regular network topology above,
the network performances of TWSR-OSN is
simulated firstly, where wavelength number of each
OISL is set to 4, 8 and 16 respectively, while each
wavelength has 16 subcarrier channels. By RWSA-
D algorithm, Figure 4 describes the network
performances with different wavelength numbers.
As expected, with the increasing wavelengths, its
network blocking probability is degraded sharply at
the same traffic load, while its network throughput
increases greatly at the same blocking probability.
For example, when the blocking probability is 0.01,
its throughput with 8 wavelengths is over 3 times of
that with 4 wavelengths, while its throughput with
16 wavelengths is over 8 times, that is, the network
throughput appears to increase rapidly at a nonlinear
rate, which reveals its advantage of the network
performance improvement by introducing two-
layered wavelength/subcarrier routing in optical
satellite networks.
Figure 4: Network performance of TWSR-OSN with
different wavelength numbers in the regular network
topology.
It is assumed that the network traffic load is
fixed, and its channel number in each ISL is set to
||||32
WS
, and the number of wavelengths |W|
changes from 1 to 32. Figure 5 illustrates the
network blocking probability by different
algorithms. The simulation result shows that AR2
algorithm appears better network performance with
lower blocking probability than FR/FF algorithm
obviously; meanwhile, once the wavelength number
|W| exceeds 4, the performance of RWSA-D
algorithm is far superior to two other algorithms.
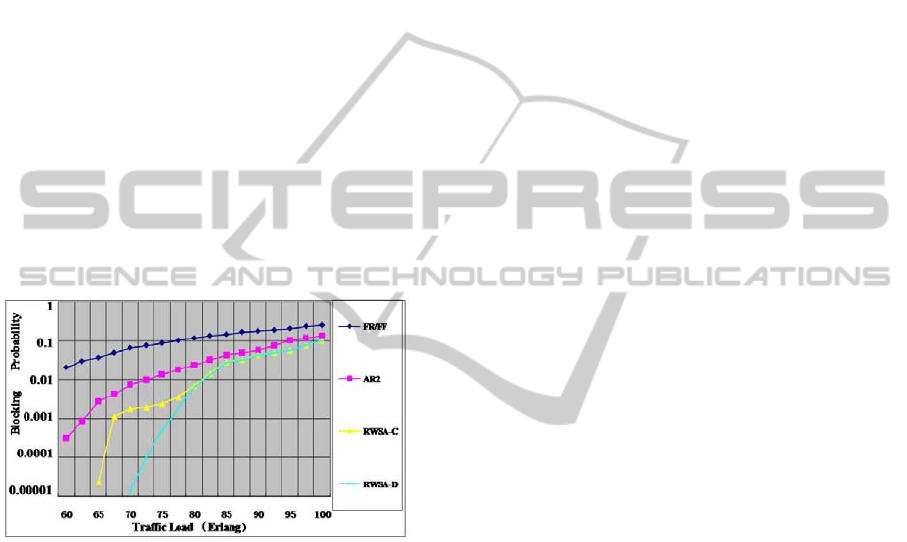
For a given irregular network topology of
TWSR-OSN, the total channel number of each OISL
is set to
||||16
WS
, while wavelength number |W|
is set to 4 and 16 separately. In Figure 6, the
blocking probability curve of RWSA algorithm
based on SL-G is compared with other algorithms,
OPTICS2014-InternationalConferenceonOpticalCommunicationSystems
74
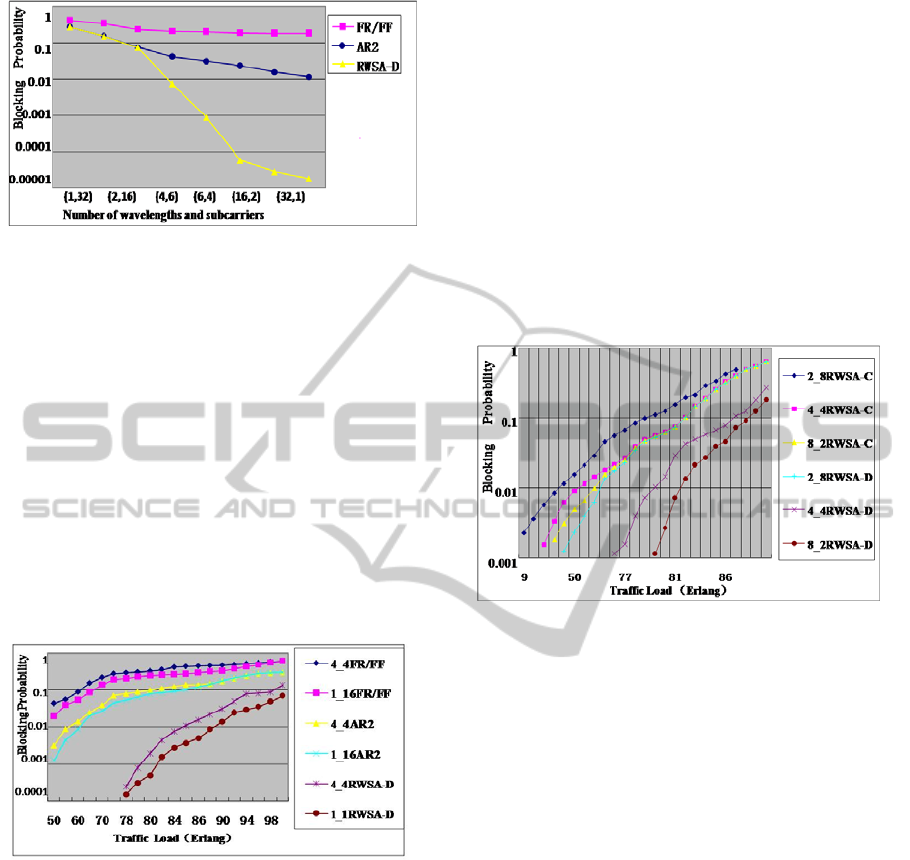
Figure 5: Network performance of TWSR-OSN with
different algorithms in the regular network topology.
based on SL-G is compared with other
algorithms, indicating similar simulation results to
the regular network topology, that is, RWSA-D
algorithm is far superior to FR/FF algorithm, and
also better than AR2 algorithm. When the network
blocking probability is 0.01, its throughput under
RWSA-D is over 1.7 times that of FR/FF, as well as
over 1.38 times that of AR2. If both wavelength
number and subcarrier channel number are set to 4
with the traffic load of 80 Erlangs, the blocking
probability by RWSA-D is only
3
1.1 10
, but the
blocking probability by FR/FF reaches up to
1
5.3 10
, and the blocking probability by AR2 is
2
9.8 10
.
Figure 6: Network performance of TWSR-OSN with
different algorithms in the irregular network topology.
Suppose that the total channel number of each
OISL is still set to
||||16WS
, while wavelength
number |W| is set to 2, 4 and 8 separately, the
performances of RWSA-D algorithm and RWSA-C
algorithm are simulated in the irregular network
topology. Figure7 shows the performance of RWSA-
D algorithm with lower blocking probability is better
than RWSA-C algorithm, while its actual difference
gap enlarges rapidly with the increasing wavelengths
|W|. For instance, when the blocking probability is
0.01, |S|=8 and |W|=2, the network throughput by
RWSA-D algorithm is 1.27 times that of RWSA-C
algorithm, while its corresponding ratio is 1.5 times
as |S|=4 and |W|
=
4, as well as 1.63 times as |S|=2
and |W|
=
8.
RWSA-C algorithm prefers to concentrate the
request callings on fewer subcarrier planes and
fewer edges, which results in so rapid exhaustion of
its channel resources that when an new calling
arrives at a node, it becomes difficult to find an
appropriate path in the subcarrier planes, even if a
large number of idle channels exist in the other
edges. Path length determined by RWSA-D
algorithm for a new calling may exceed that of
RWSA-C algorithm, but a long subcarrier path will
not necessarily lead to congestion, yet better
network performance probably.
Figure 7: Network performance of TWSR-OSN by
RWSA-D algorithm and RWSA-C algorithm in the
irregular network topology.
B: TWSR-OSN with non-uniform wavelength
distribution and the same link costs
In actual satellite networks of hybrid
constellations, owing to its different functions and
optical transceiver costs in different satellite
constellations, different types of OISLs appears non-
uniform wavelength distribution generally with its
different number of wavelengths, including inter-
satellite OISLs at the same orbit, different orbits and
different constellations. An OISL wavelength-
number matrix
WL
in the given irregular network
topology is followed below. Herein each element
indicates the wavelength number in the OISL of the
corresponding pair of nodes, and its element 0
represents no OISL between the corresponding
satellite node pair, meanwhile the subcarrier channel
number in each wavelength is set to |S|=4.
ResearchonRoutingandWavelength/SubcarrierAssignmentAlgorithmBasedonLayered-graphModelinOpticalSatellite
Networks
75
0884020004
8080200040
8800004400
4000400000
2000404000
0040040400
0040004040
0400000402
4000000020
WL
(13)
Figure 8 depicts the network performance of
different algorithms with non-uniform wavelength
distributions. It is observed that RWSA-D algorithm
and RWSA-C algorithm based on SL-G are still
better than FR/FF and AR2 algorithms significantly.
Especially, as the load is 75 Erlangs, the blocking
probability by RWSA-D algorithm is merely
4
6.5 10
, however the blocking probability of AR2
and FR/FF algorithms are
2
1.05 10
and
2
9.5 10
respectively; as the load is reduced to 70 Erlangs,
the blocking probability of RWSA-D algorithm is
lower than AR2 by two orders of magnitude, and
lower than FR/FF by three orders of magnitude.
Figure 8: Network performance of different algorithms
with non-uniform wavelength distributions.
6 CONCLUDING REMARKS
In this paper, a novel dynamic RWSA algorithm is
proposed to realize its two-layered routing and
wavelength/subcarrier assignment in TWSR-OSN.
Based on the two-level switching, a new SL-G
model is established, which can convert the RWSA
problem into finding the shortest path with limited
costs in the corresponding subcarrier layered graph,
therefore TWSR-OSN not only can provide the end-
to-end service access and aggregation for subcarrier
channel connection requests, but also its dynamic
RWSA problem can be achieved simultaneously.
By definitions of different edge cost functions in
SL-G, two types of network resource assignment
strategy of centralized strategy and decentralized
strategy are analysed, while two RWSA algorithms
are introduced, adapting to TWSR-OSN with
different kinds of constellations. Simulation results
demonstrate that, no matter whether TWSR-OSN
has single constellation with uniform wavelength
distribution or hybrid constellations with non-
uniform wavelength distribution, the proposed
RWSA algorithms based on SL-G model are
superior to traditional routing and wavelength
assignment algorithms, achieving lower network
blocking probability; Meanwhile RWSA-D
algorithm with balanced use of network resources is
better than RWSA-C algorithm that encourage the
centralized utilization of network resources.
REFERENCES
Sodnik Z., Furch B., Lutz H., 2010. Optical Intersatellite
Communication. IEEE Journal of Selected Topics in
Quantum Electronics, 16(5):1051-1057.
Yang Q., Tan L., Ma J., 2010. Analysis of Crosstalk in
Optical Satellite Networks with Wavelength Division
Multiplexing Architectures. Journal of Lightwave
Technology, 28(6):931-938.
Yang Q., Tan L., Ma J., 2009. Analysis of Doppler-effect
on satellite constellations with wavelength division
multiplexing architectures. Chinese Optics Letters,
7(1):19-22.
Baroni S., Bayvel P., 1997. Wavelength requirements in
arbitrarily connected wavelength-routed optical
networks. Journal of Lightwave Technology,
15(2):242-251.
Tan L., Yang Q., Ma J., Jiang S., 2010. Wavelength
Dimensioning of Optical Transport Networks Over
Nongeosychronous Satellite Constellations. Journal of
Optical Communications and Networking, 2(4):166-
174.
Guo Y., Miki T., Wang D., 2003. A novel scheme of
Multi-protocal subcarier/lambta Label Switching.
Joural of Electronics & Information and Technology,
26(8):1300-1305.
Poo G., Zhou Y., 2006. A new multicast wavelength
assignment algorithm in wavelength-routed WDM
networks. Journal on Selected Areas in
Communications, 24(4):2-12.
Cardoso F., Costa A., Francês L., 2010. A New Proposal
of an Efficient Algorithm for Routing and Wavelength
Assignment in Optical Networks. Joural of
Communication and Information Systems, 25(1):11-
18.
OPTICS2014-InternationalConferenceonOpticalCommunicationSystems
76
