Fuzzy Rule Bases Automated Design with Self-configuring

Evolutionary Algorithm

Eugene Semenkin and Vladimir Stanovov

Department of System Analysis and Operations Research, Siberian State Aerospace University,

“Krasnoyarskiy Rabochiy” avenue, 31, krasnoyarsk, 660014, Russia

Keywords: Genetic Fuzzy Systems, Fuzzy Rule Base Classifiers, Automated Design, Evolutionary Algorithms.

Abstract: Self-configuring evolutionary algorithm of fuzzy rule bases automated deign for solving classification

problems, which combines Pittsburgh and Michigan approaches, is introduced. The evolutionary algorithm

is based on the Pittsburgh approach where every individual is a rule base and the Michigan approach is used

as a mutation operator. A self-configuration method is used to adjust probabilities of the usage of selection,

mutation and Michigan part operators. Testing the algorithm on a number of real-world problems

demonstrates its efficiency comparing to several other commonly used approaches.

1 INTRODUCTION

Today the most popular methods for the automated

design of fuzzy rule bases and fuzzy systems are

evolutionary algorithms. Genetic algorithms (GA)

are mostly used, as well as their modifications, so

this field received the name of genetic fuzzy systems

(Cordon et al., 2001). The techniques for forming

fuzzy controllers take a special place here, but in this

paper we will focus on classification problems

solving.

The first works on data classification with fuzzy

rule bases appeared in the 90’s (Wang et al., 1992),

and several methods were developed, for example

(Alcala et. al., 2007) and (Fernández et. al, 2009). In

most of the works the design of a fuzzy logic system

was transformed into the problem of choosing rules

from a predefined set of good individual rules. There

are basically two approaches – the Michigan

approach (building rules) and the Pittsburg approach

(building an entire rule base). The first method

allows the formation of individual rules which

describe some part of the sample, but without a rule

base, so that classification is impossible. The second

method forms an entire rule base and is much more

difficult in terms of computational efforts, but it

provides a ready solution to the problem. Today

there appear more and more methods that combine

these two approaches (Bodenhofer et. al., 1997).

In this paper we consider a modification of an

algorithm, combining the Pittsburg and Michigan

approaches, that was described in (Ishibuchi et al.,

2005). One of the disadvantages of this algorithm, as

well as of any other evolutionary method, is the

existence of several genetic operators that influence

the properties of the search algorithm and must be

properly adjusted according to each problem. So, it

seems reasonable to use some self-configuration

methods, which adjust the operators’ application

probabilities during the algorithm run.

2 CLASSIFICATION WITH

FUZZY RULE BASES

Let the classification problem be given in n-

dimensional space with m measurements and M

classes. Every measurement is represented as a

vector x

=(x

, x

… x

), p=1…m. We assume that

every variable has been normalized into the [0,1]

interval. The rules used look as follows:

: if X

is A

q,1

and X

is A

q,2

and … and X

q,n

then

X is from class C

with level CF

is a rule, A

q,i

is a fuzzy set, C

is the number of

the corresponding class, CF

is the rule weight. This

is the standard rule representation, which is used in

classification problems. Unlike some other

representations, this rule has a weight CF

, which is

determined using the learning sample.

318

Semenkin E. and Stanovov V..

Fuzzy Rule Bases Automated Design with Self-conﬁguring Evolutionary Algorithm.

DOI: 10.5220/0005062003180323

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 318-323

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

There are four different variables’ space partitions

into 2, 3, 4 and 5 fuzzy sets plus a “don’t care” term,

so that a coded rule is an integer string with a

number from 0 to 14.

Figure 1: Fuzzy sets partitions.

The class number C

and the weight value CF

are captured separately. The “don’t care” term

means that the value of this variable is not

considered in the rule. This kind of technique allows

the creation of more general rules, reduces their

number and length, and gradually simplifies the rule

base. The compatibility grade of a certain

measurement x

in the rule R

is calculated as the

product of compatibility grades over all the

variables. For the ignored variables the compatibility

grade is considered as equal to one. Alternatively, a

minimum operator can be used instead of

multiplication.

The class number and the weight value are

calculated based on the confidence value in the same

way as in (Ishibuchi et al., 2005). For the rule R

the

class C

, is set if the confidence value for this class

is maximal among all other classes. If the confidence

value is less than 0.5, the rule is not generated. The

classification procedure is performed using the

winner-rule principle. This means that the rule that

has the highest product of compatibility by the

weight value is the winner rule. The measurement is

classified into the class number equal to the winner

rule class.

3 HYBRID EVOLUTIONARY

ALGORITHM OF FUZZY RULE

BASES FORMATION

The developed algorithm implements the Ishibuchi

approach (Ishibuchi et al., 2005). This algorithm can

be described in the following way:

 Population initialization;

 Rule bases fitness calculation;

 Selection, crossover, mutation;

 Applying the Michigan part to every individual;

 Forming a new generation;

 If the stop condition is satisfied, then exit, else

go to step 2;

The Michigan part contains the following steps:

 Classify the learning sample with a rule base and

set the rules’ fitness;

 Generate or delete rules from the population with

one of the methods;

 Return the obtained rules base into the Pittsburg

part.

The number of rules in the algorithm is not fixed

and it can be changed for every individual.

Nevertheless, the maximum number of rules is set.

So, the rule base is a matrix where every row is the

rule. Some of these rules can be muted and have

zero weight. During the initialization step every rule

of the rule base is formed based on randomly

selected examples from the learning sample. To

form a rule, the compatibility grades are calculated

for every term, and the greater these numbers are,

the more chances this fuzzy set has of being

included in the rule.

The fitness is calculated as a combination of

three objectives: the error in the learning sample in

percent, the number of rules in the base and the

overall length of all the rules. For the first criterion

the weight is equal to 100, and for the two others –

1. Multi-objective approaches can also be used, and

there are several examples, such as (Fazzolari et al.,

2013).

In a genetic algorithm, three selection types are

used – fitness proportional, rank-based and

tournament selection with a tournament size of

three. The crossover operator combines the genetic

information of parents and generates a new rule base

using the parents’ rules. The number of rules for the

offspring is equal to a random number from 1 to the

overall number of parents’ rules, if it does not

exceed the stated maximum number of rules.

The mutation operator is almost the same as the

mutation in standard GA, i.e. the mutation

probability depends on the number of rules and for

an average mutation equal to 1/(n*|S|), |S| is the

number of rules in the rule base. The weak and

strong mutations have probabilities 1/(3*n*|S|) and

3/(n*|S|) respectively in this algorithm.

The Michigan stage contains two main

operations – adding new rules and deleting them.

There are three possible types of Michigan stage –

only adding new rules, only deleting rules, and

replacement of rules by deleting and adding new

rules instead. The adding of new rules involves two

methods – genetic and heuristic. The heuristic

method includes new rules into the base, which are

formed using the misclassified measurements from

the sample in the same way as during the

initialization procedure. In the genetic method the

FuzzyRuleBasesAutomatedDesignwithSelf-configuringEvolutionaryAlgorithm

319

number of objects classified by this rule is used as a

fitness value. The rules are selected, then they

undergo crossover and mutation to form an

offspring. The tournament selection, uniform

crossover and average mutation are used. The

genetic and heuristic approaches are applied with

probability of 0,5. During the deleting procedure the

rules with the lowest fitness are removed from the

base.

The number k of deleted or added rules depends

on the current number of rules in the base and is

calculated so that 5(k-1) < |S| <= 5k. If the number

of rules in the base reaches the given maximum

number, new rules are not added to it.

The forming of a new population in the Pittsburg

part includes the best offspring and parents into the

new generation.

4 EVOLUTIONARY

ALGORITHM

SELF-CONFIGURATION

TECHNIQUE

Self-configuration means setting the application

probabilities of evolutionary operators based on the

success of the operators. Self-configuration needs to

be used as the algorithm efficiency highly depends

on the operators used.

The applied self-configuration method

(Semenkin et al., 2012-1) is based on encouraging

those operators which received the highest total

fitness in the current generation. This approach has

proved its efficiency in the solving of hard real

world optimization problems (Semenkin et al., 2012-

2, Semenkin et al., 2014) and has been

recommended for practical use.

Let z be the number of different operators of i-th

type. The starting probability values are set to

=1/z. The success estimation for every type of

operator is performed based on the averaged fitness

values:

, 1, 2,...,

vgFit i z







where n

is the number of offspring formed with i-th

operator, f

is the fitness value of j-th offspring,

obtained with i-th operator, AvgFit

is the average

fitness of the solutions, obtained with i-th operator.

Then the probability of applying the operator,

whose AvgFit

value is the highest among all the

operators of this type, is increased by (zK-K)/(zN),

and the probabilities of applying other operators are

decreased by K/(zN), where N is the number of

evolutionary algorithm generations, K is the constant

equal to 0,5.

The probabilities of the selection operators, the

mutation operators and the Michigan operators are

adjusted during the algorithm operation. In the first

generation equal probabilities are applied to all the

operators. For example, for the Michigan operators,

the probabilities of adding, deleting and replacement

procedures are equal when the algorithm starts.

5 ALGORITHM

IMPLEMENTATION AND

TESTING RESULTS

One of the advantages of this algorithm is that for

every rule in the base the compatibility grades for

every variable, as well as the class number and

weight, can be calculated only once and then

updated only for those rules that changed during the

algorithm run. This allows the sample to be used

fewer times, that results in a better computation

time.

Six heterogeneous classification problems from

the UCI repository (Asuncion et al., 2007) and the

KEEL repository (Alcalá-Fdez et al., 2009) were

chosen for the approach performance evaluation,

namely:

 Australian credit card problem, 690 instances, 14

variables, 2 classes – Australian;

 German bank client classification problem, 1000

instances, 24 variables, 2 classes – German;

 Image segments classification problem, 2310

instances, 19 variables, 7 classes – Segment;

 Text recognition sections classification problem,

5472 instances, 10 variables, 5 classes –

Pageblocks;

 Nasal and oral sounds classification problem,

5404 instances, 5 variables, 2 classes, –

Phoneme;

 Satellite image pixels classification problem,

6435 instances, 36 variables, 6 classes, –

Satimage.

To measure the classification quality the 10-fold

cross-validation procedure was used. In this method

the sample is split into 10 parts, 9 of them are used

as a learning sample, and the residual part as a test

sample, and then the parts are exchanged with each

other. The procedure is performed 10 times, so that

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

320

all the instances have been in the test sample at least

once. All the cross-validation procedures were

repeated three times, and the accuracy values on the

test and learning samples were averaged.

The maximum number of rules was set to 40 for

all the problems, the number of individuals in the

population – 100, the number of generations – 500,

the minimum probability of operators’ application

for self-adjustment – 0,125. Neural network models

and SVMs were built for all the problems using the

STATISTICA 10 program.

To see the effect of self-adjustment on the

algorithm performance, a set of tests of the standard

algorithm were performed with the parameters

presented in table 1.

Table 1: Algorithm configurations.

Configuration Selection type Mutation type

Proportional

Weak

2 Average

3 Strong

Rank

Weak

5 Average

6 Strong

Tournament (2)

Weak

8 Average

9 Strong

The next table represents a comparison of the

self-configured and standard algorithm efficiency for

six problems. The average classification rate of the

standard algorithm is also included.

Table 2: Test sample classification rates.

Cfg. Austr. Germ. Segm. Phon. Page. Satimage

1 0.839 0.701 0.791 0.784 0.920 0.790

2 0.839 0.707 0.790 0.790 0.931 0.785

3 0.841 0.710 0.767 0.789 0.932 0.782

4 0.872 0.759 0.880 0.805 0.942 0.831

5 0.869 0.748 0.888 0.807 0.950 0.840

6 0.861 0.768 0.893 0.810 0.947 0.835

7 0.857 0.743 0.878 0.806 0.939 0.827

8 0.860 0.746 0.885 0.810 0.945 0.836

9 0.874 0.743 0.883 0.806 0.950 0.830

Avg.

Std.

0.857 0.736 0.851 0.801 0.934 0.817

Self-

conf.

0.857 0.749 0.876 0.806 0.945 0.833

On average the self-configured algorithm

appears to be better than the standard algorithm but

worse than the best standard configuration for the

corresponding problem. One should mention that the

best results obtained by the standard algorithm were

found using different configurations for the different

problems solved. That is, the end user trying to solve

his/her problem in hand with fuzzy classifiers

designed automatically with a genetic algorithm can

occasionally choose the wrong configuration with a

very low performance. A self-configuring genetic

algorithm can guarantee at least average

effectiveness.

The accuracy of the self-configured algorithm on

the learning and test samples compared to alternative

methods are shown in tables 3 and 4. The

implemented method is called FHEA (Fuzzy hybrid

evolutionary algorithm).

Table 3: Learning accuracy.

Algorithm

FHEA SVM

Neural

Network

Problem

Australian 0.910 0.858

0.923

German 0.801 0.786

0.863

Segment 0.914

0.932

0.909

Pageblocks 0.958 0.944

0.966

Phoneme

0.830

0.768 0.815

Satimage 0.843

0.876

0.843

Table 4: Testing accuracy.

Algorithm

FHEA SVM

Neural

Network

Problem

Australian

0.857

0.826 0.852

German 0.749

0.770

0.758

Segment 0.876

0.926

0.898

Pageblocks 0.945 0.923

0.951

Phoneme

0.806

0.761 0.794

Satimage 0.835

0.870

0.819

As one can see from the tables, the proposed

algorithm has comparable results with other methods

for all the classification problems. For example, for

the phoneme problem it has shown even better

results than SVM and ANN.

It should be remembered that the main advantage

of FHEA is its ability to automatically design fuzzy

classifiers that give us “if-then” rules which can be

easily interpreted by a human. At the same time,

ANNs and SVMs, giving slightly better

computational results, cannot exhibit any kind of

transparency as they are “black boxes”.

One should also mention that the algorithm

performs quite fast, although the speed is not

comparable to specialized program systems. For

example, for the Australian problem the calculation

time is about 25 seconds. However this “drawback”

has no practical importance for the design of

classifiers that takes usually many hours.

To demonstrate the self-configuration procedure,

a graph showing the adjustment of the probabilities

FuzzyRuleBasesAutomatedDesignwithSelf-configuringEvolutionaryAlgorithm

321

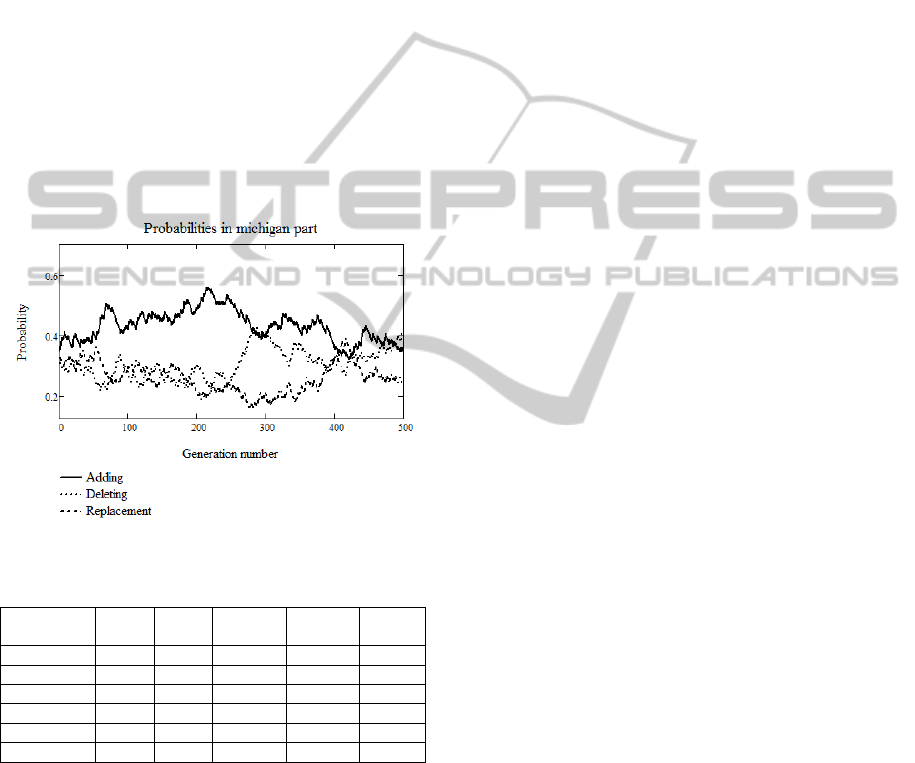
is shown in Figure 2. The graphs demonstrate the

change in the different Michigan operators’

probabilities during one of the runs. The testing was

performed for the Australian problem.

In the first stages, good fitness improvements can

be obtained by adding new rules to the base, so the

probability for adding increases as we can see and

the two others decrease. However, later, at about the

250

generation, the rule deleting operator becomes

as important as rule adding operator. At the stage of

about the 400

generation all three operators have

equal importance for a short time period, i.e. the

replacement operator receives resources back from

the other two. And, at the end of process, the

replacement operator again loses its importance. As

one can see, computational resources are actively

redistributed when the algorithm is executed.

Similar graphs can be obtained for the other

operator types.

Figure 2: Probabilities change during the algorithm run.

Table 5: Rule bases parameters.

Problem Learn Test

Number

of rules

Rule

length

Time

Australian 0.910 0.864 17,7 4,1 25.4s

German 0.801 0.748 22,3 5,3 48.9s

Segment 0.914 0.878 16,5 7,7 556s

Pageblocks 0.958 0.942 7,90 4,4 309s

Phoneme 0.830 0.807 12,2 2,7 313s

Satimage 0.843 0.822 27,8 16,6 822s

Also during the algorithm run the number of

rules in the best obtained solution, as well as the

average rule length, was captured. Table 3 contains

the averaged values of these parameters for all the

test problems. The number of rules is adjusted by the

algorithm and is different for every problem.

As an example, the rule base for the Pageblocks

(10 variables, 5 classes) problem is shown below. It

contains 7 rules with an average length of 5.28. The

learning accuracy with this rule base is 0.964, and

the testing accuracy is 0.959.

 If X

is A

and X

is A

and X

is A

and X

then class 4 with weight 1;

 If X

is A

and X

is A

and X

is A

then class 1

with weight 0.869;

 If X

is A

and X

is A

and X

is A

and X

is A

and X

is A

and X

is A

and

is A

then class 3 with weight 0.693;

 If X

is A

and X

is A

and X

is A

and X

is A

then class 4 with weight 0.775;

 If X

is A

and X

is A

and X

is A

and X

is A

and X

is A

and X

is A

and X

is A

and X

is A

then class 0 with weight 0.584;

 If X

is A

and X

is A

and X

is A

and X

is A

and X

is A

then class 0 with weight 0.932;

 If X

is A

and X

is A

and X

is A

then class

2 with weight 1.

6 CONCLUSIONS

In this paper, the self-configuring evolutionary

algorithm for automated design of fuzzy rule bases

was considered.

This method is much like the genetic algorithm,

which is often used to form fuzzy systems, but it has

the ability to adjust the number and the length of

rules, has special crossover and initialization

operators and the Michigan part. The Michigan part

of the algorithm allows accurate adjustment of rule

bases for the classification problem using

misclassified objects for building new rules. It also

deletes the rules that describe only a small part of

the sample to simplify the rule base. The algorithm

can find accurate and small rule bases quite quickly,

and its performance is comparable to other well-

known methods.

Further improvements of this approach may

include the use of multi-objective techniques and

some speed optimization.

ACKNOWLEDGEMENTS

This research is supported by the Ministry of

Education and Science of Russian Federation within

State Assignment № 2.1889.2014/K.

The authors express their gratitude to Mr.

Ashley Whitfield for his efforts to improve the text

of this article.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

322

REFERENCES

Alcala R., Alcala-Fernandez J., Herrera F., Otero J.

Genetic learning of accurate and compact fuzzy rule

based systems based on the 2-tuples linguistic

representation, International Journal of Approximate

Reasoning 44. – 2007. – p. 45–64.

Alcalá-Fdez J., L. Sánchez, S. Garcia, M. J. del Jesus, S.

Ventura, J. M. Garrell, J. Otero, C. Romero, J.

Bacardit, V. M. Rivas, J. C. Fernández, and F. Herrera,

KEEL: A software tool to assess evolutionary

algorithms for data mining problems, Soft Comput.,

vol. 13, no. 3, pp. 307–318, Feb. 2009.

Asuncion A., D. Newman, 2007. UCI machine learning

repository. University of California, Irvine, School of

Information and Computer Sciences. URL:

http://www.ics.uci.edu/~mlearn/MLRepository.html.

Bodenhofer U., Herrera F. Ten Lectures on Genetic Fuzzy

Systems // Preprints of the International Summer

School: Advanced Control—Fuzzy, Neural, Genetic. –

Slovak Technical University, Bratislava. – 1997. p. 1–

69.

Cordon O., F. Herrera, F. Hoffmann and L.

Magdalena, Genetic Fuzzy Systems. Evolutionary

tuning and learning of fuzzy knowledge bases,

Advances in Fuzzy Systems: Applications and Theory,

World Scientific, 2001.

Fazzolari M., R. Alcalá, Y. Nojima, H. Ishibuchi, F.

Herrera, A Review of the Application of Multi-

Objective Evolutionary Fuzzy Systems: Current Status

and Further Directions. IEEE Transactions on Fuzzy

Systems, 21:1 (2013) 45-65.

Fernández A., Jesus M., Herrera F. Hierarchical fuzzy rule

based classification systems with genetic rule selection

for imbalanced data-sets International Journal of

Approximate Reasoning 50. – 2009. – p. 561–577.

Ishibuchi H., T. Yamamoto, Rule weight specification in

fuzzy rule-based classification systems, IEEE Trans.

Fuzzy Systems 13 (2005) 428–435.

Semenkin E., Semenkina M. Self-configuring Genetic

Algorithm with Modified Uniform Crossover Operator

// Y. Tan, Y. Shi, and Z. Ji (Eds.): Advances in Swarm

Intelligence. – Lecture Notes in Computer Science

7331. – Springer-Verlag, Berlin Heidelberg, 2012. –

P. 414-421.

Semenkin, E. S., Semenkina, M. E. The Choice of

Spacecrafts' Control Systems Effective Variants with

Self-Configuring Genetic Algorithm // Ferrier, J.L. et

al (Eds.): Informatics in Control, Automation and

Robotics: Proceedings of the 9th International

Conference ICINCO’2012. – Vol. 1. – Rome: Italy,

2012. – P. 84-93.

Semenkin E., Semenkina M. Stochastic Models and

Optimization Algorithms for Decision Support in

Spacecraft Control Systems Preliminary Design //

Informatics in Control, Automation and Robotics. -

Lecture Notes in Electrical Engineering, Volume 283.

– Springer-Verlag, Berlin Heidelberg, 2014. – P. 51-

65.

L. X. Wang, J. M. Mendel, Generating fuzzy rules by

learning from examples, IEEE Transactions on

Systems, Man, and Cybernetics 22:6 (1992) 1414-

1427.

FuzzyRuleBasesAutomatedDesignwithSelf-configuringEvolutionaryAlgorithm

323