Quadrupedal Locomotion Based in a Purely Reflex Controller
C
´
esar Ferreira
1
, Vitor Matos
1
, Cristina P. Santos
1
and Auke Ijspeert
2
1
Industrial Electronic Department, University of Minho, Azurem Campus, Guimar
˜
aes, Portugal
2
Biorobotics Laboratory, EPFL, Lausanne, Switzerland
Keywords:
Quadruped Locomotion, Reflexes, Sensory Information.
Abstract:
Quadruped locomotion in irregular and unknown terrains is still a problem to solve. The concept of reflexes is
used in this work to contribute for the continuous search of answers about this theme. Biological researches
show that spinal reflexes are crucial for a successful locomotion in the most varied terrains, so robotics inves-
tigation in this area could be a great advance in the robot’s locomotion.
In this work, we present a sensory driven reflex controller, capable of generating locomotion in a quadruped
compliant robot. This controller is totally dependent on sensory information, so the robot’s movements are the
result of the robot interactions with the environment. Results show that the proposed controller is capable of
generating movements in a flat terrain and is resilient to unexpected perturbations such as a small ramp.
1 INTRODUCTION
It is generally accepted that locomotion in animals is
generated at the spinal cord level by a combination of
central pattern generators (CPG) and reflexes(Geyer
and Herr, 2010),(Kimura et al., 2007). In order to
achieve adaptation to irregular terrains, the robot must
have ”motor intelligence”(Cruse et al., 1998), and
adapts its moves according to unexpected situations.
Animals show an efficient solution to the locomotion
problem and so appear as an interesting alternative to
mimic in robotics.
Locomotion generation is largely dependent on re-
flexes: animals react to specific stimulus by generat-
ing particular movements. In fact, Charles S. Sher-
rington (Burke, 2007), defended that rhythms could
be the result of a chain of reflexes triggered and gov-
erned by external sensorial events, producing the final
rhythmic locomotor activity. Even though locomo-
tion is a centrally generated process, sensory feedback
plays an important role in the adaptation and correc-
tion of legged locomotion (see (Pearson, 2004) for an
important review).
It has been shown that the CPG and locomo-
tion generation is highly integrated and dependent on
feedback pathways. For instance, it has been demon-
strated (Rossignol et al., 2006) that sensory events
can adjust the duration of the rhythmic activity, stim-
ulation of sensory afferents can elicit locomotion and
sensory removal deteriorates locomotor abilities, such
as precise foot placement. Moreover, the generation
of locomotion is adapted according to sensory infor-
mation, and this occurs at different levels.
All these aspects evidence the fact that locomo-
tion generation is much more complex than a simple
feedforward process of muscle activations. In this pa-
per, we further tackle this problematic and we propose
a purely sensory-driven reflex controller inspired on
biological studies performed in animals, mainly cats.
The proposed controller is only based on the inter-
actions of the robot with the environment, therefore
sensory information is a crucial element in the move-
ment of the robot. The goal is to accomplish a parsi-
monious controller, resorting to the minimum number
of reflexes to produce a successful quadruped walking
behavior. The final controller should be able to gener-
ate a sequence of motor actions triggered by external
sensory events, accomplishing stepping motor behav-
iors. Moreover, the quadruped robot should be able
of avoiding small external disturbances of the ground
such as small ramps. It is assumed that the final tra-
jectories are not previously known, and should result
from the interplay between the motor actions and the
sensory information. The walking behavior should be
an emergent realization of motor actions reflecting the
general rules as encoded in the reflexes, and not a re-
sult from strict tracking of a predefined desired be-
havior.
Locomotion has also been achieved by the appli-
cation of simple sensory driven reflexes rules, both in
324
Ferreira C., Matos V., P. Santos C. and Ijspeert A..
Quadrupedal Locomotion Based in a Purely Reflex Controller.
DOI: 10.5220/0005062403240331
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 324-331
ISBN: 978-989-758-039-0
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

simulations and in robotic platforms (Geyer and Herr,
2010; Cruse et al., 1998). Several works comprising
CPG and reflexes have been made in the last twenty
years. In the earliest studies with reflexes Ekeberg
and Wadden implemented a neuronal model of a sin-
gle leg, that combines properties of mechanical and
neuronal systems(Wadden and Ekeberg, 1998). Cruse
et al. projected a bio-inspired controller of a hexa-
pod robot that generates locomotion based on sen-
sory events(Cruse et al., 1998). Kimura et al. pre-
sented various quadruped robots, Patrush, Tekken,
Tekken2, capable of walk dinamically on irregular
terrain, using nervous system models based on CPG
and reflexes(Kimura et al., 2000),(Fukuoka et al.,
2003),(Kimura et al., 2007). Based on Ekeberg work,
Maufroy
et al.
presented a simulation model of the
two hind legs of a quadruped robot, which also has a
controller based on CPG and sensory events(Maufroy
et al., 2008). An implementation on the Oncilla robot
is also described in (Ajallooeian et al., 2013a; Ajal-
looeian et al., 2013b). Finally, Geyer and Herr pre-
sented a muscular model of human locomotion only
controlled by muscle reflexes, exploiting principles of
legged mechanics(Geyer and Herr, 2010).
Most of the presented works on reflex based loco-
motion are implemented in simulation, using models
of musculoskeletal fore and hind legs, with the so-
lution producing muscle activations, or the torques
to be applied at the joints calculated from the mus-
culoskeletal models. Considering only reflexes, the
work by H. Cruse and the work by W
¨
org
¨
otter are ap-
plied to rotational controlled DOFs in robots. In the
case of H. Cruse the generator outputs the joint veloc-
ities for the hexapod robot, and in W
¨
org
¨
otter’s work,
the locomotion generator outputs motor voltages for
the biped robot. However, in all these works three
sensory events are used to trigger locomotor actions
(reflex based walking) or regulate the rhythm activity
of the CPGs. In common is the use of the angle of
the hip joint, regulating the timing of the stance and
swing phases. It is also used the signals indicating
ground contact from foot sensors, or even leg load,
used to inhibit the transition from the stance phase to
the swing phase.
The proposed controller is based on these works.
The proposed reflex system controls a quadruped
robot with position controlled hips and retractable,
passive compliant knees. Some of these reflexes ex-
press motor activities as a continuous activity depend-
ing on sensory information, e.g. ground contact pro-
moting/reinforcing the stance phase of the step. It is
therefore assumed that joint velocity is the best ab-
straction for the output of the system based on the
reflexes. Reflexes reflect a rate of change depen-
dent on sensory information, producing motor actions
while a determinate sensory condition is maintained,
or mimic positive feedback mechanisms found in the
motor control of animals. This assumption accepts
that joint positions change while necessary, and sen-
sory events determine the final output trajectory.
Simulations were produced in the simulated On-
cilla quadruped robot with position controlled hips
and retractable, passive compliant knees. Results
show that the projected controller fulfills the required
goals. Further, the robot becomes quite resilient to
external disturbances, such as small ramps.
2 REFLEX-BASED QUADRUPED
LOCOMOTION
We define some bio-inspired conditions for the suc-
cess of quadruped locomotion:
(a) The hip position is key factor in the transition be-
tween the stance and swing phases (Grillner and
Rossignol, 1978),(McVea et al., 2005),(Pearson,
2008);
(b) The stimulation of the footpad promotes the
stance phase (Duysens and Pearson, 1976);
(c) The unloading of the leg is a necessary condi-
tion for swing phase initiation (Hiebert et al.,
1994),(Hiebert et al., 1995),(Pearson, 2008);
3 REFLEX NETWORK
The proposed sensory-driven controller, depicted in
figure 1, includes four distinct modules: sensory in-
formation , sensor neurons, external inputs and phase
neurons, as described in the following.
It is considered that one step cycle is divided into
four motor actions: Lift-off - reduction of the leg
length by flexing the knee; Swing - bring the leg for-
ward by acting on the hip; Touchdown - having the
leg in the rostral (to the front) position, increase the
leg length to support the foot on the ground, by ex-
tending the knee; Stance - propulsion of the robot by
acting on the hip.
These motor actions are not mutually exclusive in
time, for example, the swing action could be executed
just after lift-off has started.
The position controlled joints track the position as
integrated from the reflex system output in joint ve-
locity,
˙
θ
i
, i = h, k for hip and knee joints, respectively.
For the hip joint: a) By specifying a positive ve-
locity for the hip joint, the leg produces the motion of
QuadrupedalLocomotionBasedinaPurelyReflexController
325

Sensory Information
GC AEP PEP
Sensor
Neurons
ʅ
GC
ʅ
AEP
ʅ
PEP
Hip
Ɏ
stance
ɲ
Ɏ
swing
ɶ
ɽ
h
Knee
Ɏ
touchdown
ɲ
Ɏ
liftoff
ɶ
ɽ
k
Excitatory conection
Inhibitory conection
Figure 1: Proposed Controller for a robot’s leg.
propulsion, reflecting the hip action in the stance; b)
A negative velocity for the hip joint transfers the leg
to the front, reflecting what happens in the swing.
For the Knee joint: a) A positive velocity in
the knee flexes the leg and decreases the leg length,
achieving lift-off; b) And a negative velocity in the
knee releases the spring, extending the leg, achieving
touchdown.
These motor actions are implemented by assign-
ing fixed rates of change, activated by discrete neu-
ron activations from a reflexive network dependent on
sensory information.
Despite the joint output generator being in the
form of velocity the desired output is the joint posi-
tion. The velocity joint output is directly dependent
on the neuronal activity of the phase neurons, as fol-
lows:
˙
θ
h
= α
h
Ψ
stance
− γ
h
Ψ
swing
(1)
˙
θ
k
= −(α
k
Ψ
touchdown
− γ
k
Ψ
liftoff
)
+ g
lim
(θ
k
− Θ
k,max
)exp
−
(θ
k
−Θ
k,max
)
2
2σ
2
(2)
+ g
lim
(θ
k
− Θ
k,min
)exp
−
(θ
k
−Θ
k,min
)
2
2σ
2
where Ψ are the phase neuron activations of the de-
scribed actions (Ψ ∈ [0, 1]), and α and γ are the fixed
rates of change for hip and knee joints. To limit the
range of activity on the knee, due to its limited range
of action, two joint limiting terms are included. Pa-
rameters g
lim
and σ define the strength and width of
the repeller, respectively. The values of Θ
k,max
and
Θ
k,min
are the maximum and minimum knee joint lim-
its, respectively.
3.1 Sensory Inputs
The sensory inputs to the reflex network translate sen-
sory events based on the leg’s sensory information:
the touch sensor of foot-pad to detect ground contact;
joint position to be able to detect the anterior extreme
position (AEP) and posterior extreme position (PEP).
These sensory events are detected through the sen-
sor neurons, µ
GC
, µ
AEP
, µ
PEP
, implemented as logis-
tic functions, activated (= 1) when the sensory values
cross a defined threshold: µ
GC
becomes active when
the touch sensor of the foot-pad exceeds a threshold;
µ
AEP
becomes active if hip exceeds the AEP angle;
and µ
PEP
becomes active if hip exceeds the PEP angle.
These neurons are implemented with sigmoid func-
tions, allowing the sensor neurons to become active
when the sensory value exceeds a certain threshold:
µ
AEP
=
1
1 + exp
−b(θ
h
−Θ
AEP
)
(3)
µ
PEP
=
1
1 + exp
b(θ
h
−Θ
PEP
)
(4)
µ
GC
=
1
1 + exp
b(F
threshold
−F
touch
)
(5)
where Θ
AEP
, Θ
PEP
and F
threshold
are the specified
threshold values; θ
h
is the measured hip joint angle
and F
touch
is the sensor reading.
3.2 Phase Neurons
A single leg is controlled by four neurons, which de-
termine the activation of the four motor actions of the
robot step cycle. Two motor actions are assigned to
the hip joint, each governed by one neuron, swing
and stance. The other two motor actions, lift-off and
touch-down are assigned to the knee joint. The ve-
locity joint output is directly dependent on the neu-
ronal activity of these phase neurons.
The reflex network is based on a non-spiking neu-
ron model. These neurons are simple leaky integra-
tors and have a output value between 0 and 1. The
excitatory (ξ
+ j
) and inhibitory (ξ
− j
) synaptic inputs
are calculated from first-order differential equations
and were adapted from (Wadden and Ekeberg, 1998),
as follows:
˙
ξ
+ j
=
1
τ

∑
i∈ϒ
+
µ
i
w
i
− ξ
+ j

(6)
˙
ξ
− j
=
1
τ

∑
i∈ϒ
−
µ
i
w
i
− ξ
− j

(7)
where j represents the phase neuron (stance, swing,
touchdown, liftoff), τ is the time constant,ϒ
+
and ϒ
−
are the sets of excitatory and inhibitory synapses, w
i
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
326

is the strength of synapse: w ∈ [0, 1] and u
i
is the out-
put value from the corresponding presynaptic neuron.
The neuron activation of the phase neurons was also
adapted from (Wadden and Ekeberg, 1998), as fol-
lows:
Ψ
j
=

1 − exp((Θ − ξ
+ j
)Γ) − ξ
− j
, if positive
0 , otherwise
(8)
The output of the neuron model reflects a mean
firing rate, between 0 and 1, and is characterized by its
time constant, the gain Γ and the activation threshold
Θ.
3.3 Network Behavior
Based on the description of the biological rules and
the four sensory events, the following behaviors are
encoded in the reflex network as excitatory and in-
hibitory connections (i stands for one leg):
• Hip reaching AEP elicits the touchdown action
on the knee, exciting the touchdown neuron, ex-
tending the knee: ϒ
+,touchdown,i
⊃
{
(µ
AEP,i
)
}
and
w
AEP,touchdown,i
= 1.
• Hip reaching AEP inhibits the continuation
of hip protraction: ϒ
−,swing,i
⊃
{
(µ
AEP,i
)
}
and
w
AEP,swing,i
= 1.
• Hip reaching PEP elicits liftoff, making the knee
flex: ϒ
+,liftoff,i
⊃
{
(µ
PEP,i
)
}
and w
PEP,liftoff,i
= 1.
• Ground contact elicits and reinforces the stance,
propelling the robot forward: ϒ
+,stance,i
⊃
{
(µ
GC,i
)
}
and w
GC,stance,i
= 1.
• Lack of ground contact excites the swing neu-
ron: ϒ
+,swing,i
⊃
{
(1 − µ
GC,i
)
}
and w
GC,swing,i
= 1.
Note the relationships between the excitations
and inhibitions of the neurons and the used biologi-
cal rules: ground contact activates µ
GC
, exciting the
stance neuron and promoting stance phase - rule (b);
hip reaching the anterior extreme position activates
µ
AEP
, inhibiting the swing neuron and exciting the
touchdown neuron - rule (a); Lack of ground contact
de-activates µ
GC
, exciting swing neuron and promot-
ing swing phase - rule (c); hip reaching the posterior
extreme position activates µ
PEP
, exciting the liftoff
neuron - rule (a);
3.4 Contralateral and Ipsilateral
Coordination
The simple reflex network depicted in figure 1 is
enough to produce stepping motions in a single leg.
Although independent leg reflex networks pro-
duce alternated stepping in a girdle, the addition of
an inhibitory contralateral connection imposes strict
alternation of step phases, preventing the execution
of simultaneous swing motor action on contralateral
legs.
Ipsilateral leg coordination is necessary to prevent
the execution of the swing motor action in ipsilateral
legs, as in a pace gait, and impose some phase re-
lationship in ipsilateral legs to achieve walk or trot
gaits. Ipsilateral coordination (fig. 2) can be achieved
by applying an inhibitory connection when a strict al-
ternation of ipsilateral legs is desired: Lack of ground
contact in the ipsilateral leg (o), inhibits the initiation
of the lift-off (in leg i): ϒ
−,liftoff,i
⊃
{
(1 − µ
GC,o
)
}
and
w
GC,liftoff,o
= 1.
The inhibitory contralateral connection (fig. 3)
comes from the contralateral ground contact sensory
neuron, to the lift-off motor action in the knee: Lack
of ground contact in the contralateral leg ( j), inhibits
the initiation of the lift-off (in leg i): ϒ
−,liftoff,i
⊃

(1 − µ
GC, j
)

and w
GC,liftoff, j
= 1.
4 SIMULATIONS
In this section we describe some Webots simula-
tions made on the compliant quadruped robot On-
cilla. The Oncilla is a small quadruped robot,
with pantograph, three-segment leg design, provid-
ing passive compliant behavior to the cable driven re-
tractable knees. It has 12 degrees-of-freedom, three
on each leg: hip-swing, hip-flap and knee. The
robot has compliant knees and the hip joints are po-
sition controlled. Pertaining videos are available at
http://asbg.dei.uminho.pt/user/1.
The reflex network is parameterized empirically
and based on other works (Wadden and Ekeberg,
1998; Maufroy et al., 2008; Ekeberg and Pearson,
2005).
The experiments are divided into two experimen-
tal setups. The first setup is intended to accomplish
the full quadruped walking on straight, flat terrain.
The second one is intended to verify the ability of the
robot to deal with perturbations, namely to climb up a
ramp with a maximum inclination of 8.9 degrees. As
far as startup conditions are concerned, the joint posi-
tions are established such that the contralateral limbs
are at the AEP and PEP positions, and initial neuron
activities are set to the respective step phase. Table
1 shows the set of parameters used for these exper-
iments, setting the sensory thresholds necessary for
the the sensory neurons and the joint output parame-
ters.
QuadrupedalLocomotionBasedinaPurelyReflexController
327

Sensory Information
GC AEP PEP
Sensory
Neurons
ʅ
GC
ʅ
AEP
ʅ
PEP
Hip
Ɏ
stance
ɲ
Ɏ
swing
ɶ
ɽ
h
Knee
Ɏ
touchdown
ɲ
Ɏ
liftoff
ɶ
ɽ
k
Sensory Information
GC AEP PEP
Sensory
Neurons
ʅ
GC
ʅ
AEP
ʅ
PEP
Hip
Ɏ
stance
ɲ
Ɏ
swing
ɶ
ɽ
h
Knee
Ɏ
touchdown
ɲ
Ɏ
liftoff
ɶ
ɽ
k
Excitatory conection Inhibitory conection
Fore Leg Hind Leg
Figure 2: Proposed Controller for ipsilateral leg coordination. The lack of ground contact inhibits the ipsilateral liftoff phase
on the knee.
Table 1: Sensory Thresholds and Joint output Parameters.
Parameters Fore legs Hind Legs
Θ
AEP
12 10
Θ
PEP
7 5
F
threshold
1 1
α
h
50 50
γ
h
400 400
α
k
300 300
γ
k
500 500
Simulations show that the robot is able to move in
a flat terrain and to go up a ramp, with a controller
only based on the robot interactions with the environ-
ment.
4.1 Flat Terrain Experiment
In this simulation the robot uses both fore and hind
girdles, thus accomplishing stepping motions of the
legs while propelling and maintaining the robot’s bal-
ance (fig. 4). First we will focus on how the sensory
events trigger the sequence of reflexes which produce
the motor actions.
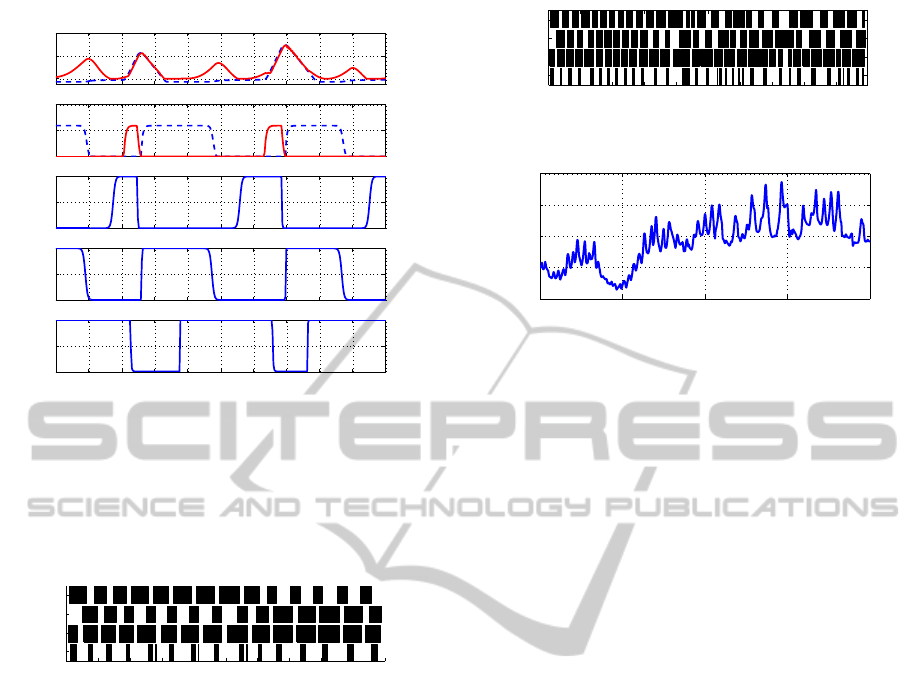
Figures 5 and 6 depict fore left leg’s hip and knee
joint movement, respectively, the phase neurons, as
well as the sequence of activation of the sensory neu-
rons. Initially, the stance neuron is active (Ψ
stance
= 1,
dashed blue line in fig. 5) due to the existence of
ground contact µ
GC
, producing a constant propulsive
motion in the hip. After the hip angle reaches the
PEP value (µ
PEP
= 1), the lift-off neuron is activated
(Ψ
liftoff
, solid red line in fig. 6), producing a flex-
ion motion of the knee, shortening the leg’s length
and lifting the foot from the ground. The lack of
ground contact (µ
GC
= 0) activates the swing neuron
Ψ
swing
(solid red line in fig. 5) which produces a flex-
ion motion of the hip, transferring the leg to a rostral
position. After reaching the AEP value (µ
AEP
= 1),
the swing neuron (Ψ
swing
, solid red line in fig. 5)
is deactivated halting the motion of the hip, and the
touchdown neuron (Ψ
touchdown
, dashed blue line in
fig. 6) becomes active, producing the extension of the
knee and the consequent foot placement. Just as the
foot regains contact with the ground (µ
GC
= 1), the
stance neuron becomes active (Ψ
stance
= 1, dashed
blue line in fig. 5) and produces the propulsive motion
of stance. The sequence repeats onwards, producing
the stereotyped motions of walking.
Figure 7 presents the obtained stepping sequence.
Note that the obtained robot stepping sequence is ir-
regular. In table 2 we present the locomotion char-
acteristics of this experiment: the swing time (T
sw
),
the stance time (T
st
), the duty factor (β) and the robot
velocity.
The obtained motor behavior can be said to re-
semble a walk, despite the lack of a constant periodic
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
328

Table 2: Locomotion Characteristics in Flat (ramp) Terrain.
Characteristics FL FR HL HR
T
sw
(s) 0.231 (0.231) 0.256 (0.235) 0.123 (0.119) 0.120 (0.124)
T
st
(s) 0.403 (0.380) 0.380 (0.374) 0.488 (0.426) 0.439 (0.434)
β 0.636 (0.622) 0.598 (0.614) 0.799 (0.781) 0.785 (0.778)
Velocity(m.s
−1
) 0.088 (0.079)
Sensory Information
GC AEP PEP
Sensory
Neurons
ʅ
GC
ʅ
AEP
ʅ
PEP
Hip
Ɏ
stance
ɲ
Ɏ
swing
ɶ
ɽ
h
Knee
Ɏ
touchdown
ɲ
Ɏ
liftoff
ɶ
ɽ
k
Sensory Information
GC AEP PEP
Sensory
Neurons
ʅ
GC
ʅ
AEP
ʅ
PEP
Hip
Ɏ
stance
ɲ
Ɏ
swing
ɶ
ɽ
h
Ɏ
touchdown
ɲ
Ɏ
liftoff
ɶ
ɽ
k
Knee
Excitatory conection Inhibitory conection
Right Leg
Left Leg
Figure 3: Proposed Controller for contralateral leg coordi-
nation. The lack of ground contact inhibits the contralateral
liftoff phase on the knee.
pattern. From the stepping sequence it is possible to
ascertain that the robot performs a walking behavior
which resembles a mix between a trot and a diagonal
sequence walk. The stepping sequence also evidences
an asymmetry along the sagittal plane, concerning the
fore legs. In the fore girdle, there is an asymmetry
in duty factor, with one leg having a greater support
duration, randomly alternating between the right fore
1
2
3
4
Figure 4: Simulation of quadruped walking using the reflex
network.
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
10
20
Hip angle
Fore left leg − Hip
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
Ψ
stance
,
Ψ
swing
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
u
PEP
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
u
AEP
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
u
GC
Time(s)
Figure 5: Fore left leg’s hip joint movement, swing and
stance phase neurons and sensory neurons. For the hip an-
gle, the dashed blue line represents the reference hip value
and the red solid line the produced joint angle. For the phase
neurons (stance and swing), the dashed blue line represents
the stance neuron and the solid red line the swing neuron.
and the left fore. In fig. 7 at around 3 s and at 6 s it is
noticeable this asymmetric pattern (red box).
Despite a not ideal stepping sequence pattern, the
robot effectively propels itself forward while main-
taining an upright posture, without falling over.
QuadrupedalLocomotionBasedinaPurelyReflexController
329

25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
20
40
Knee angle
Fore left leg − Knee
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
Ψ
touchdown
,
Ψ
liftoff
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
u
PEP
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
u
AEP
25 25.2 25.4 25.6 25.8 26 26.2 26.4 26.6 26.8 27
0
0.5
1
u
GC
Time(s)
Figure 6: Fore left leg’s knee joint movement, touchdown
and liftoff phase neurons and sensory neurons. For the knee
angle, the dashed blue line represents the reference knee
value and the red solid line the produced joint angle. For
the phase neurons, the dashed blue line represents the touch-
down neuron and the solid red line the liftoff neuron.
0 1 2 3 4 5 6 7 8 9 10
HR
HL
FR
FL
Time (s)
Figure 7: Oncilla stepping sequence pattern in flat terrain.
4.2 Climbing a Ramp
Figure 8 presents the obtained stepping sequence for
the climbing ramp scenario, when the robot has to
climb a ramp of 8.9 degrees. In table 2 we present
the locomotion characteristics of this experiment.
The robot is capable of dealing with ramps even
though it does not have specific mechanisms to do so.
It goes up with difficulty and the sequence stepping
gets worse, but propulsive stepping was produced.
This shows up the intrinsic robustness of the con-
troller. The figure 8 shows the robot walking patterns
in the ramp and although its irregularity, it is percep-
tible the walking movement of the robot. Compar-
ing the obtained values in table 2 we can see that the
robots velocity decreased in the climbing ramp situa-
tion, as expected.
Figure 9 shows the body pitch angle of the robot
in the ramp climbing situation.
0 2 4 6 8 10 12 14 16 18 20
HR
HL
FR
FL
Time (s)
Figure 8: Oncilla stepping sequence pattern on a ramp.
0 5 10 15 20
−5
0
5
10
15
Pitch angle
Time(s)
Figure 9: Robot’s body pitch angle when going up a ramp.
5 CONCLUSION
In this contribution we present a purely reflex neu-
ral controller capable of generate stable locomotion
in a quadruped robot. This work is the first step in
the development of a bio-inspired controller capable
of generating robust locomotion in many types of en-
vironments.
Future work includes the implementation of more
reflexes to improve the robot locomotion and add
noise to the sensory system to test the robot’s behav-
ior. We also want to implement a evaluation stabil-
ity system to validate our experiments and finally add
a feed-forward component in order to have a robust
controller.
ACKNOWLEDGEMENTS
This work has been supported by FCT – Fundac¸
˜
ao
para a Ci
ˆ
encia e Tecnologia within the Project Scope
PEst OE/EEI/UI0319/2014.
REFERENCES
Ajallooeian, M., Gay, S., Tuleu, A., Sprowitz, A., and
Ijspeert, A. J. (2013a). Modular control of limit cycle
locomotion over unperceived rough terrain. In Intelli-
gent Robots and Systems (IROS), 2013 IEEE/RSJ In-
ternational Conference on, pages 3390–3397. IEEE.
Ajallooeian, M., Pouya, S., Sproewitz, A., and Ijspeert, A. J.
(2013b). Central pattern generators augmented with
virtual model control for quadruped rough terrain lo-
comotion. In Robotics and Automation (ICRA), 2013
IEEE International Conference on, pages 3321–3328.
IEEE.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
330

Burke, R. E. (2007). Sir charles sherrington’s the integra-
tive action of the nervous system: a centenary appre-
ciation. Brain, 130(4):887–894.
Cruse, H., Kindermann, T., Schumm, M., Dean, J., and
Schmitz, J. (1998). Walkneta biologically inspired
network to control six-legged walking. Neural net-
works, 11(7):1435–1447.
Duysens, J. and Pearson, K. (1976). The role of cutaneous
afferents from the distal hindlimb in the regulation of
the step cycle of thalamic cats. Experimental Brain
Research, 24(3):245–255.
Ekeberg,
¨
O. and Pearson, K. (2005). Computer simulation
of stepping in the hind legs of the cat: an examination
of mechanisms regulating the stance-to-swing transi-
tion. Journal of Neurophysiology, 94(6):4256–4268.
Fukuoka, Y., Kimura, H., and Cohen, A. H. (2003). Adap-
tive dynamic walking of a quadruped robot on irreg-
ular terrain based on biological concepts. The Inter-
national Journal of Robotics Research, 22(3-4):187–
202.
Geyer, H. and Herr, H. (2010). A muscle-reflex model that
encodes principles of legged mechanics produces hu-
man walking dynamics and muscle activities. Neural
Systems and Rehabilitation Engineering, IEEE Trans-
actions on, 18(3):263–273.
Grillner, S. and Rossignol, S. (1978). On the initiation of
the swing phase of locomotion in chronic spinal cats.
Brain research, 146(2):269–277.
Hiebert, G. W., Gorassini, M. A., Jiang, W., Prochazka, A.,
and Pearson, K. G. (1994). Corrective responses to
loss of ground support during walking. ii. comparison
of intact and chronic spinal cats. Journal of neuro-
physiology, 71:611–611.
Hiebert, G. W., Whelan, P. J., Prochazka, A., and Pearson,
K. G. (1995). Suppression of the corrective response
to loss of ground support by stimulation of extensor
group i afferents. Journal of neurophysiology.
Kimura, H., Fukuoka, Y., and Cohen, A. H. (2007). Adap-
tive dynamic walking of a quadruped robot on natu-
ral ground based on biological concepts. The Interna-
tional Journal of Robotics Research, 26(5):475–490.
Kimura, H., Fukuoka, Y., and Nakamura, H. (2000).
Biologically inspired adaptive dynamic walking of
the quadruped on irregular terrain. In ROBOTICS
RESEARCH-INTERNATIONAL SYMPOSIUM-, vol-
ume 9, pages 329–336.
Maufroy, C., Kimura, H., and Takase, K. (2008). Towards a
general neural controller for quadrupedal locomotion.
Neural Networks, 21(4):667–681.
McVea, D., Donelan, J., Tachibana, A., and Pearson, K.
(2005). A role for hip position in initiating the swing-
to-stance transition in walking cats. J Neurophysiol,
94:3497–3508.
Pearson, K. (2008). Role of sensory feedback in the con-
trol of stance duration in walking cats. Brain research
reviews, 57(1):222–227.
Pearson, K. G. (2004). Generating the walking gait: role
of sensory feedback. Progress in brain research,
143:123–129.
Rossignol, S., Dubuc, R., and Gossard, J.-P. (2006). Dy-
namic sensorimotor interactions in locomotion. Phys-
iological reviews, 86(1):89–154.
Wadden, T. and Ekeberg,
¨
O. (1998). A neuro-mechanical
model of legged locomotion: single leg control. Bio-
logical cybernetics, 79(2):161–173.
QuadrupedalLocomotionBasedinaPurelyReflexController
331