Hand-projector Self-calibration Using Structured Light

Christian S. Wieghardt and Bernardo Wagner

Institute for Systems Engineering, Real Time Systems Group

Leibniz Universit

at Hannover, Appelstrae 9A, D-30167 Hannover, Germany

Keywords:

Self-calibration, Pattern Projection, Structured Light System, Motion Estimation.

Abstract:

This paper describes two methods for determining the extrinsic calibration parameters of a projector with

respect to the robot hand. One of them simultaneously solves the transformation between a camera with

respect to the robot base. Self-calibration means that no sort of calibration rig like a chessboard is needed.

Since the projector has no exteroceptive capabilities, a camera is placed in the environment or rigidly attached

to the robot base to detect the projected pattern. At different robot conﬁgurations correspondences between

the camera and projector are established to recover the transformation between them up to an unknown scale

factor. The common known formulations AX = XB and AX = ZB can be arranged in a linear form with

respect to the unknown extrinsic parameters and scale factors, and solved in least square sense.

1 INTRODUCTION

In robotics, a projector is typically used as an inter-

face or as a sensor in combination with at least one

camera. Recent developments have lead to a signif-

icant decrease in projector size, which facilitates the

usage in mobile applications. In our case, we are in-

terested in tracking the robot end-effector by means of

the projector. Because of the mobility we propose the

set-up shown in Figure 1. In order to apply a projector

appropriately on a robot hand, its homogeneous trans-

formation to the manipulator has to be determined.

This external calibration is addressed in this paper.

The main challenge is the restraint of calibration

rigs. They are not allowed by deﬁnition of self-

calibration. For calibration it is essential to move

the robot arm to different poses and capture the mo-

tions of the projector. But with no known objects

or constraints it is impossible to link the projector to

the environment. However, by detecting the relative

pose between the camera and the projector the hand-

projector transformation is still recoverable.

The projector can be described as the inverse of

the pinhole model - equal to most cameras. There-

fore we can identify the cameras and projectors intrin-

sic parameters with camera calibration based meth-

ods e.g. (Zhang, 2000). We assume that these

internal unknowns are determined beforehand with

one of the structured light system calibration meth-

ods, such as (Zhang and Huang, 2006) or (Moreno

Figure 1: An LED pico projector AXAA P2 Jr mounted

on the KUKA youBots manipulator and a uEye camera

UI-1241LE-C-HQ on its platform.

and Taubin, 2012). The camera duality furthermore

enables the use of techniques known from existing

Hand-Eye-Calibrations. This problem was ﬁrst ad-

dressed in (Shiu and Ahmad, 1989) and (Tsai and

Lenz, 1989). Later works considered simultaneous

robot-workspace calibration (Zhuang et al., 1994),

(Dornaika and Horaud, 1998), which allows the cali-

bration of an external camera. Of interest to our work

is (Andreff et al., 2001), where an unknown scale fac-

Wieghardt C. and Wagner B..

Hand-projector Self-calibration Using Structured Light.

DOI: 10.5220/0005065200850091

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 85-91

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

tor in the camera motion is incorporated.

So far, there are few publications with hand-

mounted projectors, that are usually calibrated only

to a second device on the robot arm. In (Reinhart

et al., 2007) a tracking system is used to manually

assign the projected points to world coordinates. Cal-

ibration was implemented with respect to the robot’s

tool ﬂange. In (De Tommaso et al., 2012) the pro-

jector is calibrated to an rgb-d camera via homogra-

phies to planes observed by both devices. Calibration

to the end-effector was not concerned. Even though

no robot arm was applied, (Gavaghan et al., 2011)

utilized a projector to reference system calibration.

Markers were mounted on the device and on a cali-

bration plane to detect both movements with a stereo

camera. Extrinsic and intrinsic calibration was done

by projecting chessboard patterns on the plane and

identifying them with the stereo camera.

Notice that an additional camera mounted beside

the projector on the end-effector would result in a

structured light system. That second device would

ease the presented calibration, because the scale is

given by the baseline. But we argue the renounce-

ment of the camera with payload and space limita-

tions of the end-effector. The device is also not nec-

essary when tracking the robot hand by means of the

projector, on which we will focus in future research.

Therein we will increase the number of cameras to

obtain higher accuracy and robustness. So the re-

verse set-up, where the camera is mounted on the end-

effector and the projector placed e.g. at the robot base,

is not relevant for us.

The presented method eases the calibration proce-

dure since the calibration rig can be omitted. Thus, no

limitations are arising by the necessity of fully cover-

ing the rig by the projection during the determination

of good calibration robot arm poses. Furthermore,

all projector-camera correspondences can be used for

calibration.

The paper is organized as follows: In Section 2 it

is shown how to obtain the transformation between

the camera and the projector up to an unknown scale

factor. Those are needed for the calibration proce-

dure discussed in Section 3. We then present the ex-

perimental results in Section 4, and ﬁnally Section 5

offers a conclusion and an outlook to some future

works.

2 RELATIVE POSE ESTIMATION

This section introduces a procedure to establish the

relative pose between the camera and the projector.

Due to the unknown environment the translation can

only be recovered up the scale factor. This reduces

the homogeneous transformation between the camera

and the projector to a three-dimensional rotation and

a two-dimensional translation. As it is assumed that

the camera’s and projector’s intrinsic parameters are

known, ﬁve unknown parameters need to be deter-

mined.

2.1 Establishing Correspondences

First of all, correspondences between the projector

and the camera are established by projecting vertical

and horizontal fringe patterns onto the environment.

The sequence of patterns is coded to match the pro-

jector points x

= (x

,1)

with the camera points

= (x

,1)

. We use Gray coded patterns, as they

are easy to implement and allow for high density of

points (Salvi et al., 2004). The sequence of the Gray

code in one direction is shown in Figure 2 (a) and one

typical captured image of fringes consisting patterns

is given in Figure 2 (b).

(a) (b)

Figure 2: (a): Gray code, (b): One image of the Gray coded

image sequence.

The pattern is temporary coded, thus the robot

hand has to keep its pose during the image capturing.

The projector pixels x

are given by the Gray code.

However, to obtain the camera pixels x

, decoding has

to be done. For each image every pixel illumination

(on/off) is speciﬁed by comparison to a reference im-

age. The Gray code position is deﬁned by the vertical

and horizontal sequence of illumination. The mean of

the covered pixels gives x

2.2 Determining the Rotation and the

Direction of Translation

The epipolar geometry describes the intrinsic projec-

tive geometry for two views. This is also applicable

for our camera/projector combination since the pro-

jector is modelled as an inverse camera. The epipo-

lar geometry depends only on the intrinsic parame-

ters and the relative pose, not on the environment’s

structure - an essential property for self-calibration.

The fundamental matrix F relates the image points to-

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

gether:

= 0. (1)

F can be transformed in a linear normalized form,

ﬁlled with all correspondences and it can be solved

in least square sense (Hartley, 1997). Notice that

even though the fundamental matrix encapsulates

the internal parameters, it can also be determined

without them. The essential matrix E will be re-

covered with the projector’s and camera’s intrinsic

matrices K

and K

E = K

. (2)

The essential matrix E has ﬁve degrees of free-

dom, depends only on the pose between the camera

and the projector and can be also expressed by:

E = [t]

R, (3)

where [t]

is an antisymmetric matrix deﬁned as

[t]





0 −t

−t





. (4)

R and t can be recovered from E and t up to scale.

(Hartley and Zisserman, 2000) extract out of the sin-

gular value decomposition of E:

E = UΣV

(5)

the four solutions:

(R,t) = (UWV

,±u

),W =





0 ±1 0

∓1 0 0

0 0 1





, (6)

one for which all points appear in front of the devices.

The solution of (6) can be further reﬁned via nonlinear

optimization methods. We minimize the reprojection

error:

argmin

R,t

∑

d(x

)

+ d(x

)

(7)

by means of the Levenberg-Marquardt algorithm, im-

plemented in (Lourakis, 2004).

3 CALIBRATION METHOD

In this Section we introduce two linear formulations

of the hand-projector calibration, one of which in-

cludes simultaneous robot-camera calibration. There-

fore we alter the hand-eye and robot-workspace cal-

ibrations to support our calibrations by taking the

unique scale factors for each pose into account. This

procedure follows (Andreff et al., 2001), who intro-

duces a linear formulation of the hand-eye calibra-

tion A

(λ)X = XB

for structure-from-motion meth-

ods, thus containing one scale factor.

3.1 Hand-projector

For hand-projector calibration we need to determine

X out of the common equation:

(λ

,λ

)X = XB

, (8)

which is supplemented with the unknown scale fac-

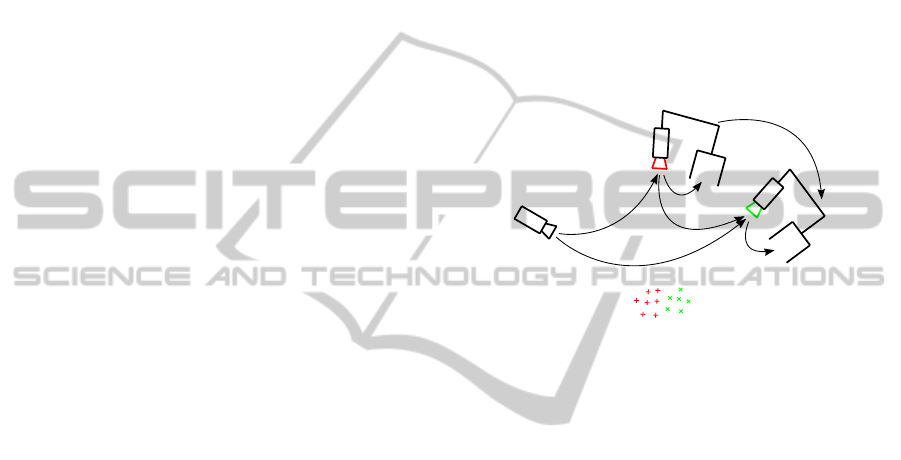
tors - see Figure 3. A

are the projectors and B

the

robot end-effectors movements. Movement i is de-

ﬁned by transformation from pose k to l:

(λ

,λ

) = P

−1

(λ

) (9)

= (R

(λ

− λ

)). (10)

Equation (8) can be split into a rotational and trans-

(λ

)

(λ

)

(λ

,λ

)

unknown environment

Figure 3: A projector is mounted on the end-effector and a

camera placed in the environment. For each movement i the

projected points change, involving different λs.

lational part:

= R

(11)

+ R

(λ

− λ

)) = R

+ t

. (12)

Using the vector operator:

vec(R) = (R

,...,R

2,1

,...,R

), (13)

which rearranges matrices into vectors and its prop-

erty on matrix multiplications (Brewer, 1978):

vec(CDE) = (C ⊗ E

)vec(D). (14)

Equation (11) can be arranged in a linear form with

respect to the unknown paramters:

vec



)



= vec (R

) (15)

⊗ R

)vec(R

) = vec (R

) (16)

⊗ R

)vec(R

) − I

vec(R

) = 0

9×1

. (17)

The same applies to the translational part (12):



⊗ t



vec(R

) + t

− R

(18)

−R

(λ

− λ

)) = 0

3×1

. (19)

Both parts result in the overall system:



− R

⊗ R

9×3

9×N

⊗ t

− R

−R







vec(R

)





= 0

12×1

(20)

Hand-projectorSelf-calibrationUsingStructuredLight

with the scale-free translation matrix and the corre-

sponding unknown scale factors:

= u

− u

, Λ = (λ

,...,λ

)

. (21)

3.2 Hand-projector and Camera-robot

Basis is the common equation:

(λ

)X = ZB

, (22)

which is supplemented with the unknown scale fac-

tors as well - see Figure 4. Here, A

are the

projector-camera and B

the robot end-effector poses.

Equation (22) can be split into a rotational and trans-

(λ

)

unknown environment

Figure 4: A projector is mounted on the end-effector and a

camera is placed in the environment or attached to robot

platform. The camera optical frame coincides with the

world frame. For each pose i the projected points change,

resulting in a new λ

lational part:

= R

(23)

+ λ

= R

+ t

. (24)

Using the vector operator and the property (Brewer,

1978) equation (23) can be arranged in a linear form

with respect to the unknown paramters:

⊗ R

)vec(R

) − I

vec(R

) = 0

9×1

. (25)

The same applies to the translational part (24):



⊗ t



vec(R

) + t

− R

− λ

= 0

3×1

. (26)

Both parts result in the overall system:



⊗ R

−I

9×3

9×N

3×9

⊗ t

−R

−U









vec(R

)

vec(R

)







= 0

12×1

(27)

with the scale-free translation matrix and the corre-

sponding unknown scale factors:

= u

, Λ = (λ

,...,λ

)

. (28)

3.3 Formulations with Known Scale

Here we give the ﬁnal single linear systems to avoid

duplicity. Following previous sections, the formula-

tions are straightforward to get. With fully known t

(20) reduces to:



− R

⊗ R

9×3

⊗ t

− R



vec(R

)





9×1



. (29)

and (27) reduces to:



⊗ R

−I

9×3

3×9

⊗ t

−R









vec(R

)

vec(R

)









9×1



(30)

3.4 Solvability

From (20) we see, that we have 12 + i unknowns and

can solve for 12i. In (27) we have 24 + i unknowns

and can also solve for 12i. Thus, at least three robot

arm poses have to be approached in both methods to

solve the homogeneous systems. Furthermore, we

notice from (Tsai and Lenz, 1989) that at least two

movements with nonparallel rotational axes are nec-

essary to get a unique solution of the hand-eye cali-

bration. This also applies for the cases with known

scale (29) and (30).

The homogeneous systems (20) and (27) are lin-

ear in the parameters and can be solved in least square

sense. Optionally, one can separately estimate the ro-

tational parameters R

and R

of the upper part and

afterwards the translational parameters t

, t

and Λ of

the lower part. Separating is reasonable having good

rotational data. Otherwise the error would propagate

into the translational data.

4 EXPERIMENTAL RESULTS

In this section the performances of both proposed

self-calibration formulations are presented. Further

comparison is given by their linear calibration equiv-

alent without any scale factors. All methods were car-

ried out in simulation and with real hardware.

Simulations validate the algorithm based on

ground truths and show the effect resulting from noisy

transformation data of the robot arm and the camera-

projector pair. Due to the increase of unknown pa-

rameters by one for each pose, less accurate results

are to be expected. This inﬂuence of the parameter

growth will also be shown in simulation by means of

their equivalents.

Since the physical robot arm and camera data

is strongly noisy, we also give a comparison to the

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

equivalents with the help of a chessboard. This out-

lines the achievable accuracy.

For evaluation, we used 135 different robot arm

conﬁgurations. The poses for computation were ran-

domly selected in a clustered manner to enlarge trans-

lation and rotation between the poses. We calculated

the rotational error e

of the estimated

R by recov-

ering its rotation vector and determine the angle be-

tween its ground truth R

, so that 0 ≤ e

≤ π is ful-

ﬁlled. The average transformations given by:

t =

∑

i=1

||t

|| + ||t

. (31)

Thus, the relative error results in e

= ||

t − t

||/

t. We

took all possible movements between the poses into

account, leading to (N − 1)N/2 homogeneous trans-

formations. All four applied formulations are listed in

Table 1 and referenced in the following by their num-

ber.

Table 1: Applied Methods.

#1 Hand-Projector

(λ

,λ

)XXB

#2 Hand-Projector and Camera-Robot

(λ

)XZB

#3 Hand-Projector, known scale

XXB

#4 Hand-Projector and Camera-Robot, known scale

XZB

4.1 Synthesized Data

For our simulation, the robot arm poses B

are uni-

formly placed on a circle and alternately rotated

around two distinguished axes at each position. This

arrangement is based on the later used manipula-

tor’s workspace. With known X and Z the projector-

camera transformation is given by:

= ZB

−1

. (32)

We considered two sources of error: Noise in

translation and noise in rotation. Both are applied to

the robot arm poses and the camera-projector trans-

formations. For translation and rotation distribution

we randomly generated unit vectors with zero mean.

Either of them were multiplied by their corresponding

Gaussian distributed standard deviation σ

and σ

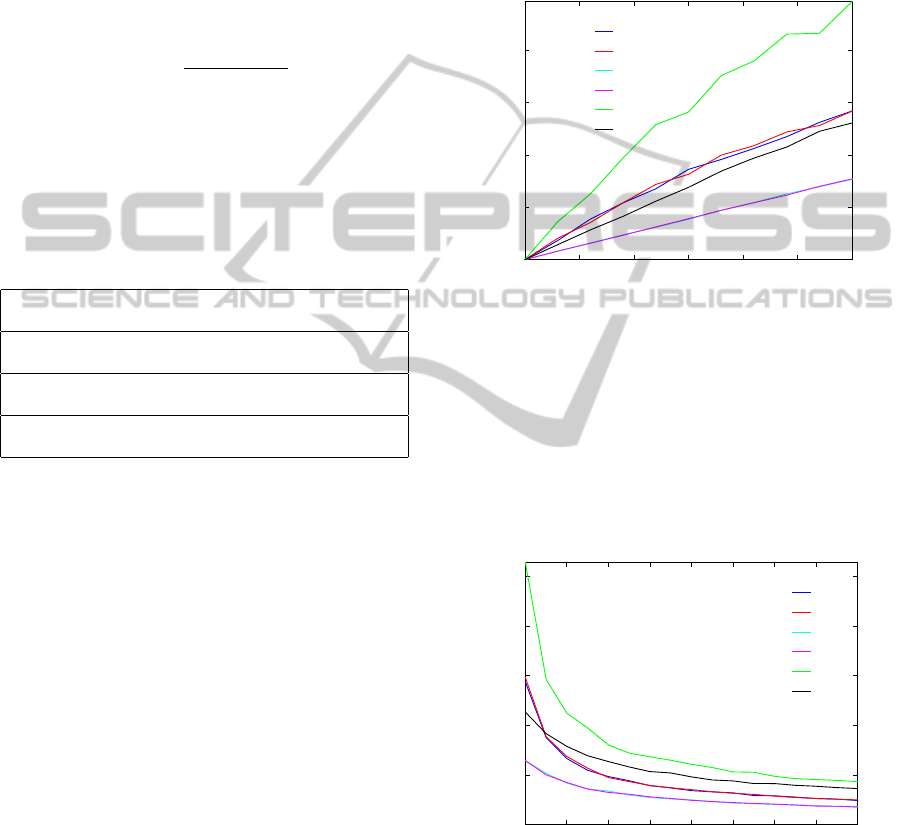
First, we show the dependency of transformation

perturbation in Figure 5 for N = 4 poses. A good cri-

terium is given by the relative position error of X,

since it is calculated for all four methods. By compar-

ing ¯e(t

#1−4

) we can conclude, that the most robust so-

lutions against translational error are #3 and #4, even

though #4 determines twice as many parameters as

#3. Whereas, incorporating the unknown scale fac-

tors Λ lead to a noticeable increase of errors in #1 and

#2. Thus, at no expense of accuracy in X one can ad-

ditionally solve for the camera pose Z. The errors of

X and Z depend on the set-up and the used manip-

ulator conﬁgurations, therefore usually deviate from

each other.

¯e

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

0.05

0.1

0.15

0.2

0 0.005 0.01 0.015 0.02 0.025 0.03

Figure 5: Average relative error of t

and t

In Figure 6 we depicted the average relative error

for different numbers of poses. We deviated the cam-

era and robot arm poses with σ

= 0.01. It is shown,

that even for a high number of used poses, a gap be-

tween the solutions #1 ↔ #3 and #2 ↔ #4 remains

due to the unknown scale factors. Again, the com-

parison of #1 ↔ #2 and #3 ↔ #4 reveals that solving

for the unknown Z does not effect the accuracy.

¯e

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

Number Poses N

0.02

0.04

0.06

0.08

0.1

4 6 8 10 12 14 16 18 20

Figure 6: Average relative error of t

and t

at σ

= 0.01.

The dependency of rotation perturbation in shown

Figure 7 for N = 4 poses. It can bee clearly seen that

the rotation uncertainty has almost the same inﬂuence

on all methods. That is due to the high weighted ro-

tational parts of the linear systems. Since the upper

parts of systems (20) resp. (27) coincide with (29)

Hand-projectorSelf-calibrationUsingStructuredLight

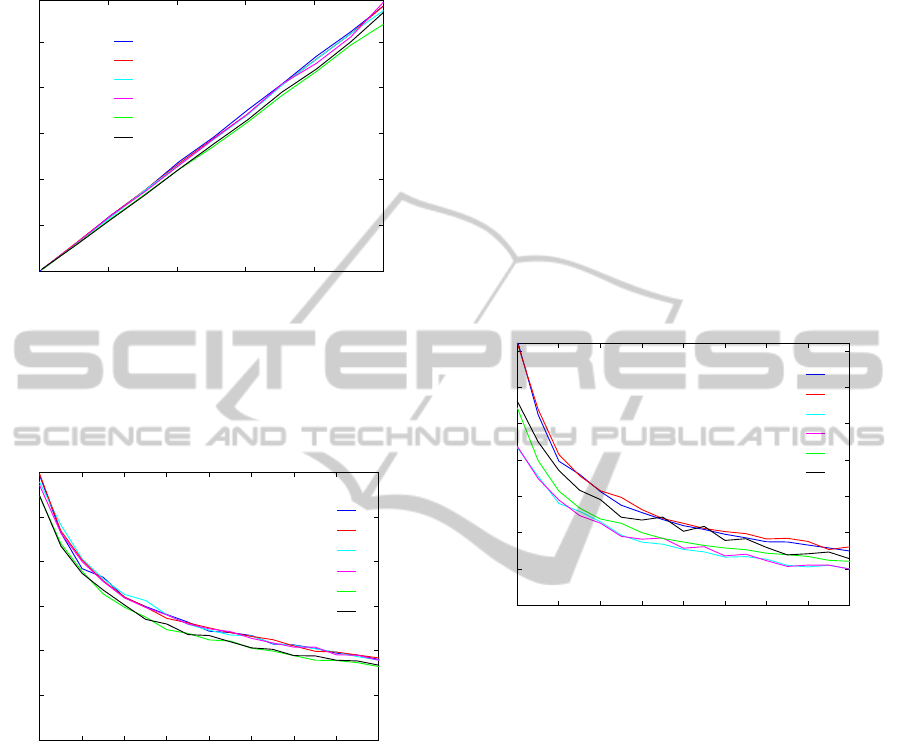
resp. (30) the average rotational errors are mostly de-

pendent of R

and R

¯e

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

0.1

0.2

0.3

0.4

0.5

0 0.2 0.4 0.6 0.8 1

Figure 7: Average rotational error of R

and R

In Figure 8 we depicted the average relative error

for different numbers of poses. We deviated the cam-

era and robot arm poses with σ

= 1.0

◦

. As assumed,

the congruence continues at more applied poses.

¯e

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

Number Poses N

0.1

0.2

0.3

0.4

0.5

0.6

4 6 8 10 12 14 16 18 20

Figure 8: Average rotational error of R

and R

at σ

1.0

◦

4.2 Real Data

The experimental set-up is shown in Figure 1. The

KUKA youBot articulated robot arm consists of ﬁve

serial rotary joints. Due to the robot arm kinematic,

the end-effector poses are limited to those planes with

the axis of the ﬁrst joint as a common line. The LED

pico projector AXAA P2 Jr at the end-effector has

a resolution of 1920x1080 pixels. The uEye cam-

era UI-1241LE-C-HQ from IDS has a resolution of

1280x1024 pixels. The presented hand-projector con-

ﬁguration is convenient since the projector is pointed

at the workspace. For full calibration, two distinct ro-

tations between the poses are necessary. This can be-

come a difﬁcult task, because the projector has to be

pointed to the same workspace in all poses. A good

rotation axis is given by the last joint since the pro-

jector’s view is just slightly changing. The second

rotation is given by the second to fourth joints. As

no ground truth is given, we select n = 1000 sets of

N = 20 poses and take the average solution.

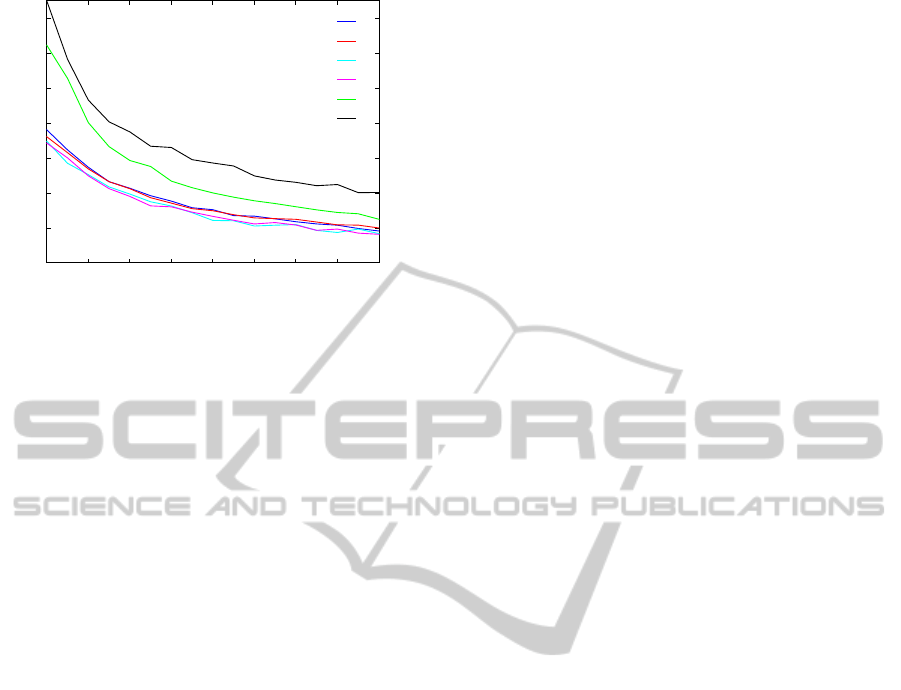
To show the ability of self-calibration, the meth-

ods #1 and #2 were applied in an unknown environ-

ment with few desktop items - see Figure 2 (b). For

methods #3 and #4 we established the projectors mo-

tion by means of a chessboard, placed in the envi-

ronment. Local homographies are used to determine

the homogeneous transformation between the projec-

tor and the camera to the chessboard (Moreno and

Taubin, 2012). The results are given in Figure 9 and

Figure 10.

¯e

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

¯e(t

)

Number Poses N

0.01

0.02

0.03

0.04

0.05

0.06

0.07

4 6 8 10 12 14 16 18 20

Figure 9: Average relative error of t

and t

over the number

of poses N.

As already shown with help of the synthesized

data, the errors of X through #1 and #2 respectively #3

and #4 coincide. Notice that in the simulation we used

the transformations X and Z determined from the real

data. The main difference is the restricted workspace

of the manipulator. With these changed manipula-

tor conﬁgurations the resulting relation of accuracies

shifts. Compared with Z, the error of X increases in

position and decreases in orientation. The effect ap-

pears in a different amount for the methods, since #1

and #2 used slightly different conﬁgurations than #3

and #4.

In this experiment, we emphasized the achiev-

able accuracy of the applied hardware. Even though

the solutions converge well compared to their move-

ments, some errors remain. Unfortunately, the biggest

source of noise can not be assigned.

As assumed, the use of chessboard gives more

accurate results, since full pose data has been used.

Figure 10 conﬁrms the good rotational data, follow-

ing the procedure of Section 2.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

¯e

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

¯e(R

)

Number Poses N

0.05

0.1

0.15

0.2

0.25

0.3

0.35

4 6 8 10 12 14 16 18 20

Figure 10: Average rotational error of R

and R

over the

number of poses N.

5 CONCLUSIONS

This paper presents two self-calibration methods for

externally calibrating a projector to a robotic hand.

One of them additionally gives the solution of the

transformation between the robot base and an exter-

nal camera.

In contrast to existing approaches, the presented

solutions need neither any additional device at the

end-effector nor any calibration unit in the environ-

ment. The capability is demonstrated by the posi-

tive results of using real hardware. Provided with

ground truth data, simulations prove the accuracy of

the methods.

It has been shown that the error that results from

the unknown scale factors quickly converges by in-

creasing the number of poses. The additional error

resulting from simultaneously estimating the camera

pose is negligible. This is beneﬁcial since the camera-

projector pair can be used as a structured light sensor.

Future works will tackle optimizing of the solu-

tion and identifying good robot arm poses for calibra-

tion. Spatial coded light will be considered, as it en-

ables us to use the method in dynamic environments.

REFERENCES

Andreff, N., Horaud, R., and Espiau, B. (2001). Robot

hand-eye calibration using structure-from-motion. In-

ternational Journal of Robotics Research, 20(3):228–

248.

Brewer, J. W. (1978). Kronecker products and matrix calcu-

lus in system theory. IEEE Trans Circuits Syst, CAS-

25(9):772–781.

De Tommaso, D., Calinon, S., and Caldwell, D. (2012).

Using compliant robots as projective interfaces in dy-

namic environments. Lecture Notes in Computer Sci-

ence, 7621:338–347.

Dornaika, F. and Horaud, R. (1998). Simultaneous robot-

world and hand-eye calibration. IEEE Transactions

on Robotics and Automation, 14(4):617–622.

Gavaghan, K., Peterhans, M., Oliveira-Santos, T., and

Weber, S. (2011). A portable image overlay

projection device for computer-aided open liver

surgery. IEEE Transactions on Biomedical Engineer-

ing, 58(6):1855–1864.

Hartley, R. (1997). In defense of the eight-point algorithm.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 19(6):580–593.

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-

etry in Computer Vision.

Lourakis, M. (Jul. 2004). levmar: Levenberg-marquardt

nonlinear least squares algorithms in C/C++. [web

page] http://www.ics.forth.gr/∼lourakis/levmar/. [Ac-

cessed on 31 Jan. 2005.].

Moreno, D. and Taubin, G. (2012). Simple, accurate, and

robust projector-camera calibration. In 3D Imaging,

Modeling, Processing, Visualization and Transmis-

sion (3DIMPVT), 2012 Second International Confer-

ence on, pages 464–471.

Reinhart, G., Vogl, W., and Kresse, I. (2007). A projection-

based user interface for industrial robots. In Proceed-

ings of the 2007 IEEE International Conference on

Virtual Environments, Human-Computer Interfaces,

and Measurement Systems, VECIMS 2007, pages 67–

71.

Salvi, J., Pags, J., and Batlle, J. (2004). Pattern codiﬁcation

strategies in structured light systems. Pattern Recog-

nition, 37(4):827–849.

Shiu, Y. C. and Ahmad, S. (1989). Calibration of wrist-

mounted robotic sensors by solving homogeneous

transform equations of the form ax = xb. IEEE Trans-

actions on Robotics and Automation, 5(1):16–29.

Tsai, R. Y. and Lenz, R. K. (1989). New technique for fully

autonomous and efﬁcient 3d robotics hand/eye cali-

bration. IEEE Transactions on Robotics and Automa-

tion, 5(3):345–358.

Zhang, S. and Huang, P. (2006). Novel method for struc-

tured light system calibration. Optical Engineering,

45(8).

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(11):1330–1334.

Zhuang, H., Roth, Z. S., and Sudhakar, R. (1994). Si-

multaneous robot/world and tool/ﬂange calibration

by solving homogeneous transformation equations of

the form ax=yb. IEEE T. Robotics and Automation,

10(4):549–554.

Hand-projectorSelf-calibrationUsingStructuredLight