
Noise Mitigation over Powerline Communication Using
LDPC-Convolutional Code and Fusion of Mean and Median Filters
Yassine Himeur
12
and Abdelkrim Boukabou
1
1
Department of Electronic, Jijel University, Jijel, Algeria
2
Centre de Développement des Technologies Avancées (CDTA), Algiers, Algeria
Keywords: Powerline Communication, OFDM, LDPC-CC, Median Filter, Mean Filter, Impulse Noise.
Abstract: In this paper, we propose a new impulse noise mitigation approach in Orthogonal Frequency Division
Multiplexing (OFDM) signals over Powerline communication (PLC) channel. Recently LDPC-
Convolutional Code (LDPC-CC) has received much interest as an alternative to LDPC codes for its
advantages and low complexity. The proposed approach exploits the redundancy introduced by LDPC-CC
and cyclic prefix (CP) added to the OFDM transmitter to recover noisy coefficients. It is based on the fusion
of median and mean of their neighboring coefficients using a window and a dynamic threshold calculated
on the basis of noise variance and the peak value of the noise in the received signal. Detection of noisy
coefficients takes into consideration the neighboring coefficients. The proposed technique presents a good
robustness to impulse noise performance without adding a big complexity to the transmission system.
Promising results have been achieved by the proposed approach when compared to filtering and coding
techniques alone.
1 INTRODUCTION
Interest in PLC technology as a broadband
multimedia connectivity solution to and within the
home continues to grow in a rapid pace. The driving
advantage of this technology is that it exploits the
already existing and ubiquitous power line
distribution infrastructure to provide broadband
multimedia services to customers. Because power
lines were originally designed for AC power
distribution at 50 Hz and 60 Hz, the characteristics
of this channel present some technical challenges for
data transmission at higher frequencies. A big
degradation can be caused by impulse noise
generated over powerline channel.
OFDM modulation, deployed in the vast majority of
today's networks is used in the PLC channel
(Anatory et al., 2009). It is a promising technique for
increasing the bandwidth of narrowband power line
communications (Lakshmi et al., 2008). Although
OFDM reduces the effect of impulsive noise in data
transmission, it is necessary to employ mitigation
techniques in order to cope with PLC channel
conditions and achieve higher data rates.
Recent investigations have studied different
approaches for noise mitigation over PLC. The
simplest of such methods is to precede the
conventional OFDM demodulator with a blanker or
a clipper (Haffenden et al., 2000). This method is
widely used in practice because of its simplicity and
ease of implementation. Theoretical performance
analysis and optimization of blanking was first
investigated by Zhidkov in (Zhidkov, 2004) and
(Zhidkov, 2006), where a closed-form expression for
the signal-to-noise ratio (SNR) at the output of the
blanker was derived and the problem of blanking
threshold selection in the presence of impulse noise
was addressed. On the other side, a multitude of
works have studied the performance of LDPC codes
on PLC channel (Tanner, 1981 and MacKay, 1999).
The authors of (Andreadou, 2007), e.g., have shown
that LDPC codes can perform better than Reed–
Solomon or convolutional codes on PLC channel. In
(Wada, 2004), it was found that the performance of
LDPC codes is superior to that of the Turbo codes
(Berrou et al., 1993) under a cyclo-stationary
Gaussian noise environment.
In this paper we present an OFDM-PLC noise
mitigation in two steps: first, we use LDPC-CC to
protect the source data, since they present more
advantages over the LDPC codes. Then, in the
second step, we use a fusion of mean and median
5
Himeur Y. and Boukabou A..
Noise Mitigation over Powerline Communication Using LDPC-Convolutional Code and Fusion of Mean and Median Filters.
DOI: 10.5220/0005065500050013
In Proceedings of the 11th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2014), pages 5-13
ISBN: 978-989-758-046-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

filter (FMMF) to compensate the impulse noise
generated over PLC channel by exploiting the
redundancy introduced by LDPC-CC and CP.
The rest of the paper is organized as follows. In
section 2 the models for OFDM system, PLC
channel and impulsive noise are reviewed. In section
3, the proposed noise mitigation approach based
LDPC-CC/FMMF is explained. Section 4 presents
the simulation results of the proposed technique in
practically proven PLC channel conditions. Then in
section 5 conclusions and perspectives are drawn.
2 SYSTEM MODEL
A general system model of indoor PLC OFDM
systems is depicted in Fig. 1. With a LDPC-CC
coded OFDM transmitter, the signal sequence to be
transmitted, given as
, is first LDPC-CC coded
and then serial-to-parallel (S/P) converted to form
the N data streams
, where 0 ≤ n ≤ N − 1. The S/P
output is subcarrier modulated using BPSK, QPSK
or QAM, etc., prior to the application of the N-point
inverse discrete Fourier transform (IDFT) process
(Canete et al., 2006), that is,
exp
2
,01
(1)
where IDFT indicates IDFT process, and
is the
subcarrier modulated signal. In order to combat
inter-channel interference (ICI) and inter-symbol
interference (ISI), OFDM uses a CP that is appended
at the start of OFDM symbols.
The output streams of
are then parallel-to-
serial (P/S) converted and used to modulate a radio
frequency (RF) carrier for transmission over the
desired communications channel.
Generally, noise in the channel can be considered
as impulsive noise (Zimmermann and Dostert, 2002)
The OFDM receiver simply reverses the
transmission process and after the RF demodulation,
the received OFDM signal
is modeled as follows:
∗
∗
(2)
where
,
, and
are the channel impulse
response, AWGN, and impulsive noise
representations, respectively. * indicates a
convolution operation and
is the aggregation of
and
. The resulting sequence
is then S/P
transformed into a parallel format and CP was being
removed. A N-point DFT process is applied:
exp
2
,01
(3)
where DFT indicates DFT process. The N-point
DFT is then P/S converted with a subcarrier
demodulation process corresponding to the
subcarrier modulation used during transmission. In
our research, the FFT and IFFT are utilized for the
implementation of DFT and IDFT, respectively.
When a channel equalizer is not considered, we can
represent
as
(4)
where
is the channel frequency response and
is impulsive noise in frequency domain.
2.1 Powerline Channel Model
The power line network differs than other
communication channels in topology, structure, and
physical properties.
In this paper, we adopt a widely accepted and
practically proven PLC multipath channel model
(Canete et al., 2011).
Numerous reflections are caused at the joints of the
network topology due to impedance variations.
Factors such as multipath propagation and
attenuation are considered when designing PLC
model.
The PLC model used is a bottom-up model
which is usually based on transmission line theory.
This approach requires perfect knowledge of the
targeting power network, including its topology, the
used power line cable and load impedances of
terminals. These network elements are modeled
mathematically so that they can be incorporated to
generate the channel. The channel model was
proposed in (Canete et al., 2011), it is shown in Fig.
2 and is based on a particularly simple topology of a
PLC network with few transmission lines and loads
to derive a parametric model that still preserves the
essential behavior of these channels in the HF band
(up to 30 MHz). The line lengths or the loads
impedance are generated from independent
statistical distributions, the topology gives a natural
correlation to the behavioral parameters of the
channel response, like the attenuation and the RMS-
DS (root mean squared delay spread).
After measuring many electrical appliances
(Canete et al., 2006), the observed behavior can be
classified into three groups: approximately constant
impedances (a not very common case); time-
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
6
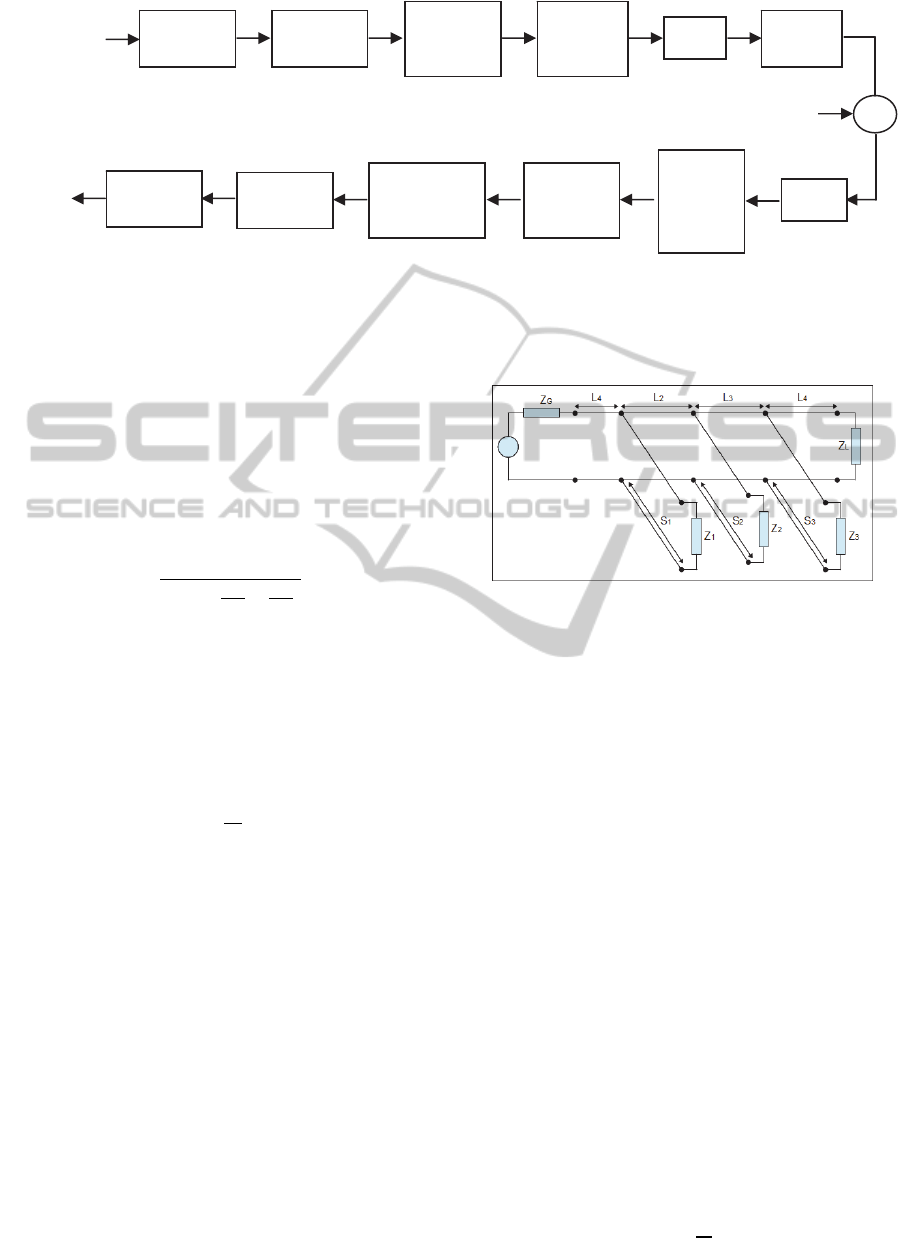
Figure 1: OFDM-PLC system model used in the simulation process.
invariant but frequency-selective impedances; and
time-varying and frequency selective impedances.
For the constant impedances, reasonable values
are {5, 50, 150, 1000, ∞}Ω. They represent,
respectively, low, RF standard, similar to
transmission line Z0, high, and open circuit
impedances. For the frequency-selective impedances
an adequate model is a parallel RLC resonant circuit,
whose impedance can be described as,
Z
w
R
1jQ
ω
ω
ω
ω
(5)
where R is the resistance at resonance;
,
resonance angular frequency; and Q, quality factor
(which determines selectivity).The second group
corresponds to a more “harmonic” impedance
variation along the mains period that can be modeled
as,
Z
ω,t
Z
ω
Z
ω
sin
2π
T
t∅;0tT
(6)
This function contains a rectified sinusoid
synchronized with the mains voltage. It has three
parameters: the offset impedance,
; the amplitude
of the variation,
; and a phase term ∅, which
serves to reference the variation with respect to the
mains voltage zero-crossing. The simplified network
layout used in PLC modeling can be observed in
Fig.2.
The model presented so far permits the
generation of PLC channels at random to create
representative channels in a statistical sense. The
generation is addressed by proposing parameter
values or ranges, based on many channel and load
measurements, and on some intuitive decisions from
the physics of the problem. The following
parameters are suggested for LTI channel generation
in the frequency band up to 30 MHz: Discrete-
frequency resolution: N = 2048 points in the positive
axis, the resolution is 14 kHz (Canete et al., 2011).
Figure 2: Network topology for the PLC model used in the
simulation.
2.2 Impulse Noise Model
Serious efforts have been made in order to find the
time and frequency characteristics of the impulse
noise ((Zimmermann and Dostert, 2002, Degardin et
al., 2002) and prevent severe signal degradations.
Interference generated by this noise at a receiver
within a PLC network can be modeled by a Poisson
model (Korki et al., 2011). The impulse noise used
in evaluation step is given by
(7)
where
is the Poisson process which is the arrival
of impulsive noise, and
is white Gaussian process
with mean zero and variance
. The arrival of
impulses is modeled according to the Poisson
process, and the impulsive noise amplitudes are
modeled based on the Gaussian process with a mean
of zero and variance σ
. This means that impulsive
noise will occur according to a Poisson distribution
with a rate λ units per second, so that the probability
of an event of m arrivals in unit time is:
P
t
P
Tt
e
λ
t!
,t0,1,2,…
(8)
+
BPSK
Ma
pp
e
r
OFDM
Modulator
(IFFT)
Fusion of
mean and
Median
Filter
(FMMF)
OFDM
Demodulator
(FFT)
Transmitted
data
PLC
Channel
BPSK
Dema
pp
e
r
Received
data
Cyclic
extension
addition
DAC
ADC
Cyclic
extension
removal
Impulse
noise
LDPC-CC
encoding
LDPC-CC
decoding
NoiseMitigationoverPowerlineCommunicationUsingLDPC-ConvolutionalCodeandFusionofMeanandMedianFilters
7

3 IMPULSE NOISE MITIGATION
SYSTEM
3.1 LDPC-Convolutional Codes
In this paper, we use a class of convolutional codes
defined by a low density parity-check matrix and an
iterative algorithm of the decoding of these codes
(Felstrom and Zigangirov, 1999) in order to reduce
the impulse noise generated over the powerline
channel.
The choice of using LDPC-CC is motivated by
the fact that it is simple to encode, since the original
code construction method yields to a shift register
based systematic encoding. It is suitable for
transmission of continuous data as well as block
transmissions in frames of arbitrary size where
LDPC can transmit only block of fixed length. For a
given complexity LDPC-CC has better performance
than LDPC block codes and has excellent BER
performance under AWGN.
An
,, regular LDPC convolutional code
is a set of sequences satisfying equation
0,
where
...
⋱ ⋱
...
⋱ ⋱
(9)
where
is the memory and is the period of the
LDPC-CC, and t ∈ Z is the time index (Felstrom and
Zigangirov, 1999). The submatrices
,
0,..., are binary matrices, where is
the number of information bits that enter the
encoder, and is the number of coded bits that exit
the encoder at a given time index. The rate of the
code is /. Submatrices
are defined as
,
...
,
⋮ ⋮
⋮ ⋮
,
...
,
(10)
The memory is equal to the largest such that
is a nonzero matrix, and .
An example parity-check matrix for 6 rate-1/2
LDPC-CC is shown in Figure 3.
The associated constraint length is defined as
1
.. The Tanner graph of an LDPC
convolutional code has an infinite number of nodes.
However, the distance between two variables nodes
that are connected by the same check node is limited
by the syndrome former memory
of the code.
Figure 3: An example parity-check matrix,
, for a rate-
1/2 LDPC-CC.
As a consequence, the decoding of two variable
nodes that are at least
1
time units apart
from each other can be performed independently,
since they do not participate in the same parity-
check equation. This allows continuous decoding
that operates on a finite window sliding along the
received sequence. Encoder structure is shown in
Fig. 4. Message passing LDPC codes decoding bases
on min-sum algorithms. The corresponding
generated from with parity check matrix is used for
decoding. The decoder will only update statistics
corresponding to the non-highlighted section of
.
It manages data flow between sub-decoder (min-sum
decoder) period and between iterations.
Figure 4: Convolutional codes encoder structure.
u
n
v
1,n
,v
2,n
h
1
0
h
2
0
h
1
M
h
2
M
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
8

|
α.+.Med
|
, if
|
|
≥
|
|
and
|
|
, if
|
|
(11)
3.2 Fusion of Mean and Median Filter
All practical Coded OFDM (COFDM) systems
contain redundancy not only in the form of an error
control code (e. g. Turbo-code or LDPC), but also in
the form of a cyclic prefix (CP), added by the
OFDM transmitter to reduce the inter-block
interference (IBI) caused by multipath propagation.
By exploiting the redundancy introduced by LDPC-
CC and CP we propose an impulse noise mitigation
based on the fusion of mean and median values of
their neighboring coefficients using a window, as
shown in Fig. 5. The window size is selected based
on the performances obtained for each size in term
of SNR and BER of reconstructed data approach that
recovers denoised OFDM coefficients of the
transmitted signal based on the fusion of median and
mean.
3.2.1 Fusion Strategy
Mean filter is arithmetic simpleness and rapid
calculation speed. But there are some disadvantages
given as follows. Signal coefficients will be blurred
by mean filter processing with equal weighting
coefficient. It is very sensitive to impulse noise, the
bad effect of the extremeness coefficients can be
diffused to other coefficients around. Also, it doesn’t
consider the relativity between signal samples. From
the analysis above, the typical mean filter algorithm
can be improved greatly by optimizing the weighting
coefficient.
Adaptive median filter can reduce the distortion
of signal through removing the extremeness value of
window and reserving the pic value with middle
level. However, with the increase of noise density,
the denoising effect of adaptive median filter gets
worse, especially when Gaussian noise exists too. In
order to achieve the better denoising effect and
preserve the signal coefficients well, mean filter
technique is necessary to be combined.
3.2.2 Noise Detection and Reduction
The detection of noisy coefficients in the received
OFDM signal is performed by calculating a noise
threshold and by comparing the central pixel in the
window to its neighbors. If the central coefficient is
bigger than the noise threshold and their neighbors,
it will be considered as a noisy coefficient and it will
replaced by the fusion of mean and median values of
neighbors as indicated in equation (11). Else if it is
bigger than the noise threshold and smaller or equal
to one of their neighbors, it will be considered as
noiseless coefficient and its value will be preserved.
where
is the noise threshold value,
and
are
the input and output of the thresholding system,
respectively.
α and denote the relative weights of
importance of mean and median filters of the
neighboring coefficients. and reprente the
mean and median values repectively.
By analyzing the effect of impulse noise on
OFDM signal, we can see that it generates a series of
peak values which have large amplitudes in
comparison with other coefficients values.
Based on the work realized by Donoho et al
(Donoho and Johnstone, 1995) and on an
experimental study, we have found that the noise
threshold
has a relation with the noise variance
and the peak value of the noisy signal. For these
reasons, we have proposed a new threshold function
that estimates noise threshold in OFDM signal, as it
is mentioned in the equation (12)
.
2.log
1
1
2
(12)
where is the signal length, is the noise variance
which is well known in wavelet literature as the
Universal threshold. It is the optimal threshold in the
asymptotic sense and minimizes the cost function
(Donoho and Johnstone , 1995).
An estimate of the noise level was defined based
on the median absolute deviation given by
|
(i)
|
0
.
6
74
5
,1,2,…,
(13)
and
max
|
(i)
|
|
(i)
|
(14)
NoiseMitigationoverPowerlineCommunicationUsingLDPC-ConvolutionalCodeandFusionofMeanandMedianFilters
9

Figure 5: The different windows used in the simulation.
Estimate the noise threshold
is a delicate task;
it must be carefully selected to minimize the BER in
the receiver. If
is too small, most of the received
samples of the OFDM signal will be clipped
resulting in poor BER performance. On the other
hand, for very large
, clipping will have a
negligible effect on the received signal, allowing
most of the impulse noise to be part of the detected
signal, hence degrading performance. Therefore, a
simulation based on the proposed method is used to
analyze the effects of different window sizes. It
seems that larger window includes more
information. However, the statistical results in Table
1 indicate that it is not so. As the window size
becoming larger, SNR declines proportionally.
Therefore, the OFDM signal coefficients are
correlated in a small neighborhood. So we choose
the window (L = 3). The proposed algorithm can be
summarized in the following steps
Step 1. Calculate the peak value of the received
noisy OFDM signal and estimate the Noise
variance using equation (14) and (13) respectively.
Step 2. Estimate the noise threshold value
using
equation (12).
Step 3. Filter the received signal using equation (11)
and a 1x3 window.
Step 4. Repeat steps 1,2 et 3 for all coefficients of
the noisy OFDM signal.
4 SIMULATION RESULTS
Matlab software was utilized to study the
performance of the proposed combined LDPC-
CC/FMMF impulsive noise mitigation technique.
A random signal is mapped into a BPSK symbols
and modulated using OFDM with 128 subcarriers
and passed through a PLC multipath channel. The
noise generated is considered as an impulse noise.
The arrival of this noise is assumed to follow a
Poisson distribution and is added to the transmitted
signal. Clipping, blanking and proposed noise
mitigation approaches are then employed in the
OFDM receiver and their performances are
compared.
Table 1: Improvement reached by the proposed adaptive
noise clipping system for different window sizes at 0 [dB].
Windows
size
SNR(d
B)
L=3 9.842
9.315 L=5
L=7 8.679
8.213 L=9
In the clipping approach, we precede the OFDM
receiver with clipping nonlinearity as indicated in
the equation (15), where
is the clipping threshold.
While in the blanking scheme we use a blanking
nonlinearity as show in the following equation (16),
where
is the blanking threshold. Note that both
nonlinearities are of amplitude type (i.e. phase of the
signal is not modified).
Different scenarios of impulsive noise, with
different impulse burst probabilities of occurrence
are considered to evaluate the performance of
proposed noise mitigation system. For the presented
work, simulation results are obtained using the
following fusion parameters, α 0.7, 1.2.
4.1 Impact of LDPC-CC
Since the performance of LDPC decoder depends on
the convolutional code period, it is reasonable to
discuss the impact of this period on the LDPCCC
performance against impulse noise. Fig. 6 shows
how this period can affect the BER.
Secondly, the effect of the impulse busts probability
is studied. Figure 7 shows how different values of
the impulse probabilities occurrence impinge the
system performance.
It is observed that when the impulse burst
probability increases, the system performance drops.
,
|
|
,otherwise
,0,1,…,1
(15)
,
|
|
0,otherwise
,0,1,…,1
(16)
OFDM coefficient
to be filteredQPSK
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
10

In fact, Fig. 7 shows a serious degradation of LDPC-
CC performance under PLC circumstances with the
increasing of impulse bursts probability. It is clear,
that LDPC-CC shows less obvious improvement
under impulse probability occurrences 0.05 and
0.1 as compared with the performance obtained
under 0.005 and 0.01.
Figure 6: Impact of convolution period on LDPC-CC
performance against impulse noise.
Figure 7: Impact of impulse noise probability on LDPC-
CC performance.
This behavior is anticipated, because when the
impulse noise lasts longer, it damages more data
blocks leading to greater errors at the receiver.
Moreover, LDPC-CC codes are designed for AWGN
reduction, the error correction capability drops to a
large extent since noise in practice differentiates
seriously from the assumed AWGN in the decoding
process
4.2 Impact of FMM Filter
A FMMF has been introduced earlier in Section 2.3
for the detection and removal of impulse noise.
Various impulse noise probabilities are considered
0.01, 0.05 and 0.1 and which implies that 1%, 5%
and 10% of the received OFDM samples will be
affected by impulse noise, respectively.
Here, we give the results obtained by comparison
of proposed FMMF against clipping and blanking
approaches. As can be observed from Fig. 8, the
proposed FMMF algorithm greatly improves the
performance in terms of BER. It has a good aptitude
for noise reduction especially with low SNR. For
example at a SNR=0 dB, more than 5% gain in BER
can be obtained.
The results of this comparative study show that
proposed HMMF performs better than the clipping
and blanking nonlinearities in the three impulse
noise scenarios. On the other hand, in a weakly
impulsive environment, clipping nonlinearity may
slightly outperform the blanking scheme.
4.3 Impact of LDPC-CC/FMMF
Data transmission is carried out on a PLC channel.
The combination of FMMF and LDPCCC helps to
improve the robustness of transmitted data against
multipath effect and impulse noise generated over
the PLC channel. In this simulation, the BER
performances of LDPC-CC/FMMF with LDPC rate-
1/2 and a convolutional code period T=256, and at
various impulse noise probabilities are illustrated in
Figure 9. As one can see, the BER results of joint
FMMF-LDPCCC system has been improved with
comparison of using only LDPCCC or FMMF alone.
For example, we have more than 12% improvement
in BER in case of applying the proposed LDPC-
CC/FMMF system at a SNR=0 in comparison with
using OFDM-PLC without a noise reduction
approach.
Also, it can be concluded from Figure 9 that
proposed LDPC-CC/HMMF scheme has more noise
reduction capability for lower impulse bursts
probabilities, as illustrated in Figure 9.a (e.g., for
0.01). While this capability is decrease with the
increasing of impulse probabilities occurrence, as
indicated in Figure 9.b and 9.c (e.g, for 0.1).
The result verifies the principle that combined
LDPC-CC/FMMF has superiority in performance
but with slower convergence speed with the
increasing of impulse probability occurrence. The
proposed scheme succeeds in improving the
performance; however the result is still not good
enough for real world application especially for high
impulse bursts probability.
0 5 10 15
10
-4
10
-3
10
-2
10
-1
10
0
EbN0[dB]
BER
OFDM
T=32
T=64
T=128
T=256
0 5 10 15
10
-4
10
-3
10
-2
10
-1
EbN0[dB]
BER
P(T=t)=0.01
P(T=t)=0.05
P(T=t)=0.1
P(T=t)=0.5
NoiseMitigationoverPowerlineCommunicationUsingLDPC-ConvolutionalCodeandFusionofMeanandMedianFilters
11

(a) (b) (c)
Figure 8: Performance comparison of FMMF, clipping, blanking nonlinearity for OFDM-Based PLC for: a) 0.01 , b)
0.05 and c) 0.1.
(a) (b) (c)
Figure 9: Performance of LDPC-CC and combination of LDPCCC and FMM filter for: a) 0.01 , b) 0.05 and c)
0.1.
5 CONCLUSIONS
From the simulation results, the Combination of
LDPC-CC and FMMF gives more enhancement in
respect of BER than using LDPC-CC or FMMF
alone. When SNR is about 12dB, the BER drops
down below 10
for 0.01 and below 10
for
0.05 and 0.1. However, the increase of
impulse probability occurrence affects LDPC-CC
capacity of noise detection and correction which can
reduce the efficacy of this decoding scheme.
As a perspective to this work, we propose to
adapt the LDPC-CC decoding process to increase
error correction capability for impulse noise.
REFERENCES
Anatory. J, Theethayi N., Thottappillil R., Mwase C. and
Mvungi. N.H., 2009. The effects of multipath on
OFDM systems for broadband power-line
communications a case of medium voltage channel. In
World Academy of Science, Eng. and Technology 54.
Andreadou N., Assimakopoulos C., Pavlidou F. N., 2007.
Performance Evaluation of LDPC Codes on PLC
Channel Compared to Other Coding Schemes, In
IEEE ISPLC, pp. 296–301.
Berrou C., Glavieux. A, Thitimajshima P., 1993. Near
Shannon Limit Error Correcting Coding and
Decoding: Turbo Codes. In Proc. IEEE Int. Conf.
Commun, pp. 1064–1070.
Canete F. J., Cortés J. A., Diez, L. and Entrambasaguas J.
T., 2006. Analysis of the Cyclic Short-Term Variation
of Indoor Power-Line Channels. In IEEE JSAC, 24(7),
pp. 1327–38.
Canete F. J., Cortés J. A., Díez L. and Entrambasaguas J.
T., 2011. A Channel Model Proposal for Indoor Power
Line Communications. In IEEE Communications
Magazine, 49(12), pp. 166–174.
Cowley N. P, Payne A., and Dawkins M., 2002. COFDM
Tuner With Impulse Noise Reduction. In Eur. Patent
Appl. EP1180851.
Degardin V., Lienard M., Zeddam A., Gauthier F., 2002.
Classification and Characterization of Impulsive Noise
on Indoor Power Line Used For Data
Communications. In IEEE Trans. on Consumer Elect.,
4( 4), pp. 913–918.
Donoho D. L. and Johnstone I. M., 1995. Denoising by
Soft Thresholding. In IEEE Trans. on Inform. Theory,
Vol. 41, pp. 613–627.
0 3 6 9 12 15 1
8
10
-4
10
-3
10
-2
10
-1
EbN0[dB]
BER
OFDM
Blanking
Clipping
FMMF
0 3 6 9 12 15 18
10
-3
10
-2
10
-1
EbN0[dB]
BER
OFDM
Blanking
Clipping
Fusion
0 3 6 9 12 15 18
10
-2
10
-1
EbN0[dB]
BER
OFDM
Blanking
Clipping
FMMF
0 2 4 6 8 10 12 14 16 18
10
-4
10
-3
10
-2
10
-1
EbN0[dB]
BER
OFDM
LDPC-CC
LDPC-CC/FMMF
0 2 4 6 8 10 12 14 16 18
10
-4
10
-3
10
-2
10
-1
EbN0[dB]
BER
OFDM
LDPC-CC
LDPC-CC/FMMF
0 2 4 6 8 10 12 14 16 18
10
-4
10
-3
10
-2
10
-1
EbN0[dB]
BER
OFDM
LDPC-CC
LDPC-CC/FMMF
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
12

Felstrom A. J., Zigangirov K Sh., 1999. Time-Varying
Periodic Convolutional Codes with Low-Density
Parity-Check Matrix. In IEEE Trans on Inf. Theory,
45(6), 2181–91.
Haffenden O. P. et al., 2000. Detection and Removal of
Clipping in Multicarrier Receivers. In Eur. Patent
Appl. EP1043874, Bull. 20000/41.
Korki M., Hosseinzadeh N., and Moazzeni T., 2011.
Performance Evaluation of a Narrowband Power Line
Communication for Smart Grid with Noise Reduction
Technique. In IEEE Transactions on Consumer
Electronics, 57(4), pp. 1598–1606.
Lakshmi A., Koomullil G., and Bapat J., 2008. Coding and
Diversity Schemes for OFDM Based Narrowband
Power-Line Communications. In International
Conference on Advanced Technologies for
Communications, (ATC), pp. 73–76.
MacKay D. J. C., 1999. Good Error-Correcting Codes
Based on Very Sparse Matrices, In IEEE Trans. Inf.
Theory 45 (3), pp. 399–432.
Tanner M., 1981. A Recursive Approach to Low
Complexity Codes, In IEEE Trans. Inf. Theory IT,
27(5): 533–547.
Wada T., 2004. A Study on Performance of LDPC Codes
on Power Line Communications. In IEEE Int. Conf.
Commun., vol. 1, pp. 109–113.
Zhidkov S. V., 2004. On the Analysisof OFDM Receiver
with Blanking Nonlinearity in Impulsive Noise
Channels. In Proc. Int. Symp. Intell. Signal Process.
Commun. Syst., pp. 492–496.
Zhidkov S. V., 2004. On the Analysisof OFDM Receiver
with Blanking Nonlinearity in Impulsive Noise
Channels. In Proc. Int. Symp. Intell. Signal Process.
Commun. Syst., pp. 492–496.
Zhidkov S. V., 2006. Performance Analysis and
Optimization of OFDM Receiver with Blanking
Nonlinearity in Impulsive Noise Environment. In
IEEE Trans. Veh. Technol., 55( 1), pp. 234–242.
Zimmermann M. and Dostert K., 'Analysis and Modeling
of Impulsive Noise in Broad-Band Powerline
Communications. In IEEE Trans. On Elect. Compt,
vol. 44, no. 1, FEBRUARY 2002.
NoiseMitigationoverPowerlineCommunicationUsingLDPC-ConvolutionalCodeandFusionofMeanandMedianFilters
13
