Adaptive Embedded Systems

New Composed Technical Solutions for Feasible Low-Power and Real-time Flexible

OS Tasks

Hamza Chniter

1,2,3

, Mohamed Khalgui

1,2

and Fethi Jarray

3,4

INSAT Institute, University of Carthage, Carthage, Tunisia

FST faculty, University of Elmanar, Elmanar, Tunisia

ISI Institute, Mednine, Tunisia

Laboratoire CEDRIC, CNAM, 292 rue St-Martin 75141, Paris cedex 03, France

Keywords:

Flexible Embedded System, Reconﬁguration, Real-time and Low-power Scheduling, Integer Programming,

Heuristic.

Abstract:

The paper deals with low-power adaptive scheduling of synchronous and ﬂexible real-time OS tasks. A soft-

ware reconﬁguration scenario is assumed to be any run-time operation allowing the addition-removal-update

of OS tasks to adapt the system to its environment under well-deﬁned conditions. The problem is that any

reconﬁguration can push the system to an unfeasible behavior where temporal properties are violated or the

energy consumption is possibly high and unacceptable. A task in the system can change its characteristics

at any time when a reconﬁguration scenario is applied, it can also be stopped or replaced by another one.

The difﬁculty is how to ﬁnd the new temporal parameters of the systems tasks after any reconﬁguration. We

use a DVS processor which is with a variable speed to support run-time solutions that re-obtain the system’s

feasibility. The challenge is how to compute the best combinations between available processor speeds for a

good compromise between execution time and energy consumption. We propose a combinatorial optimization

method based on integer programming and heuristics. We propose also a solution when the available speeds

do not allow the feasibility of the system. Both approaches include a mechanism to adjust the deadlines of

tasks to satisfy the feasibility conditions and overcome the problem of rejected tasks. This mechanism makes

the scheduling more ﬂexible and able to react in accordance with its environment.

1 INTRODUCTION

An embedded system(ES) is a device with a dedi-

cated function including hardware and software parts

which form a unique component of a larger physical

system which is expected to run without human in-

tervention. The embedded systems should often run

under real-time constraints that determine their relia-

bility and correctness (Liu and Layland, 1973; Barr,

2007; Heath and Steve, 2003). ES are designed to

control many devices in common use today to meet

a large range of user requirements. Modern embed-

ded systems are often based on microcontrollers and

integrated in more complex systems to perform spe-

ciﬁc tasks (Heath and Steve, 2003). The goal is to

optimize it in order to reduce the size, the cost of the

product, and increase the reliability as well as perfor-

mance. Some embedded systems also have real-time

performance constraints that must be met for many

reasons such as safety and usability. Others may have

power constraints that can be violated after particu-

lar reconﬁguration scenarios. A conﬁguration sce-

nario is assumed as a runtime software intervention

which act on the system state to allow the addition-

removal-update of OS tasks and consequently adapt

the system to its environment under functional and

extra-functional requirements. A reconﬁguration can

change the system behavior where temporal prop-

erties are violated or the energy consumption over-

comes its limit and push the system to a unfeasible

state. One challenge with embedded systems is de-

livering predictably good performance on monitoring

and controlling. In fact, embedded systems have hard

real-time requirements: if computations are not com-

pleted before a deadline, the system will fail, possi-

bly injuring users and can causes many side effects.

Hence the challenge for real-time system researchers

is to develop approaches to design fast systems with

Chniter H., Khalgui M. and Jarray F..

Adaptive Embedded Systems - New Composed Technical Solutions for Feasible Low-Power and Real-time Flexible OS Tasks.

DOI: 10.5220/0005066000920101

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 92-101

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

high predicted performance that must provide real-

time response. When a processor is running, reconﬁg-

urable embedded systems can undergo different dis-

turbances into their environments due to a reconﬁg-

uration scenario (Imran Raﬁq Quadri et al., 2012).

This can lead to the violation of temporal constraints

such as deadlines, increasing in energy consumption

and following a non-feasible system. Conﬁguration

scenarios can be a result of the addition-removal-

update of the tasks in the system. To reach a sys-

tem that gather between providing real-time responses

and low-power consumption, modern embedded sys-

tems integrate new processor technology called DVS

(Dynamic Voltage Scaling)(PARAIN et al., 2000) al-

lowing to dynamically change the processor speed of

OS tasks to make tradeoff between the energy con-

sumption and the execution time. Each processor

will have a set of available operating speeds which

it can operate with. This technology tries to change

the voltage of the chip which is related with the pro-

cessor speed and the duration of tasks execution (He

et al., 2012). The difﬁculty lies in determining the

best scaling factor of voltage for the whole system at

any instant when a reconﬁguration occurs in order to

achieve a new behavior or implementation of the sys-

tem that meets all timing constraints and consumes

less energy. To overcome the problem, we propose a

combinatorial optimization approach based on integer

programming (Hladik et al., 2008), and fast heuristic

(Jeannenot et al., 2004)). The objective is to ﬁnd the

optimal scaling factor in order to obtain a new fea-

sible system after any reconﬁguration such as adding

new tasks to the system. The approach tries to give

additional solutions when the processor drains all the

available scaling factors and the system lies unfeasi-

ble. Those solutions try to adjust the deadlines of the

tasks by using fast optimization approaches to provide

a more ﬂexible system that can properly be adapted to

its environment when any overload condition occurs.

The remainder of this paper is organized as follows.

In Section 2, we discuss the originality of this paper

by studying the state of the art. In section 3, we ex-

pose the problem. We present in Section 4 some ter-

minologies and the contribution dealing with integer

program formulation and proposed heuristic to ﬁnd

the optimal scaling factors and adjusted deadlines. Fi-

nally, numerical results are presented and discussed in

Section 5.

2 RELATED WORKS

Nowadays, real-time reconﬁgurable systems need

more and more solutions for ﬂexible and adaptive

scheduling of their tasks under power constraints. The

problem of real-time scheduling is classically to en-

sure the execution of all the tasks at run-time with-

out missing the deadlines where the total energy con-

sumption is minimized (Letters, 1996). The use of

maximum scaling factor of the processor can acceler-

ate the execution time of all tasks and meet the tem-

poral constraints. This can produce signiﬁcant en-

ergy consumption that exceeds the system capacity,

hence the fact to vary the scaling factor during ex-

ecution becomes a need. A new technology known

as DVS(Dynamic Voltage Scaling) (PARAIN et al.,

2000) is integrated in the new processors for this

purpose to dynamically change the processor speed.

Choosing the suitable scaling factor for the tasks

to ensure the best compromise between the execu-

tion time and the energy consumption remains the

most desired constraint. Several studies have been

performed in this context such as integer program-

ming (Hladik et al., 2008), graph traverse (Heilmann,

2003), branch and bound (Xu, 1993). In (Fang and

Lin, 2013), the authors presented a linear integer pro-

gram to solve the problem by applying DVS tech-

nique for mobile computing platforms. In (cic¸ek and

Celik, 2011) and (Fidanova, 2006), the low-power

scheduling problem was studied for parallel proces-

sors architecture, a simulated annealing and a tabu

search approaches were proposed to solve the prob-

lem. Each task can be divided into a number of parts

called sub-tasks, and each part must be executed on

a separate processor. In (Ying and Cheng, 2010), it

was assumed that all the processors are available and

each processor can handle work on time without pre-

emption. In addition, each arriving job can be pro-

cessed properly. The author in (He et al., 2012) tries

to solve the problem by breaking down the processor

to active and inactive state. He presents a mechanism

to adjust the supply voltage depending on the load

working system for low-power energy consumption.

Genetic algorithms have been also applied to solve

the scheduling problems for multiprocessor schedul-

ing periodic dependent tasks such as in (Nossal, 1998;

Dalfard and Mohammadi, 2012). Two approaches

was proposed in (Chniter et al., 2014) to solve the

scheduling problem in a reconﬁgurable real-time sys-

tem. The objective is to determine the suitable pro-

cessor scaling factor which meet the corresponding

deadlines and to decrease the energy consumption. In

another way and to reach a ﬂexible system that react

correctly with it environment, (Chantem et al., 2009;

Dwivedi, 2012) present an elastic real-time model

based on period and deadline adjustment. The objec-

tive is to ﬁnd a solution for rejected tasks in the sys-

tem by changing the period or deadline of OS tasks.

AdaptiveEmbeddedSystems-NewComposedTechnicalSolutionsforFeasibleLow-PowerandReal-timeFlexibleOS

Tasks

Among this category, there are those which try to

solve the problem of real-time scheduling by ﬁxing

the adequate scaling factor of processor for a fea-

sible system with a low-power energy consumption.

Nevertheless, no one in related works addresses this

problem by using integer programming and heuristics

to allow optimal reconﬁguration real-time scheduling

with power constraints. In addition, they did not con-

sider the case when all the available scaling factors

with which the processor can operate, may not guar-

antee a solution for violated temporal constraints. In

this case, the system may not react in accordance with

its environment and can miss interesting tasks. Other

works like (Buttazzo et al., 1998; Chantem et al.,

2009; Dwivedi, 2012) try this problem but they did

not take into account the energy constraints. They try

to ﬁnd the adjusted parameters without ﬁxing the ex-

ecution sequence of tasks.

In the present paper we propose an elastic method to

determine the appropriate scaling factor of processor

for a feasible reconﬁgurable system with a low-power

energy consumption. If the system lies unfeasible,

a proposed solution based in deadline adjustment is

used to meet the new requested constraints after re-

conﬁguration. The proposed method produces the op-

timal scaling factor of processor, new adjusted dead-

lines and the execution sequence of tasks.

3 PROBLEM AND NOTATIONS

We assume a reconﬁgurable real-time system to

be composed of periodic independent synchronous

tasks. A reconﬁguration scenario is any run-time

operation allowing the addition-removal-update

of tasks to adapt the system to its environment.

Nevertheless, the application of a scenario can

increase the energy consumption or push some tasks

to violate the corresponding deadlines. Our goal is to

provide some solutions that will optimize the energy

consumption and guarantee the respect of deadlines

after each reconﬁguration scenario. We propose an

Integer Programming model and a heuristic to ﬁnd

the required solution by changing the scaling factor

of the processor. We construct also a mechanism

that will be applied when no available scaling factor

can fulﬁll the system requirements. This mechanism

is based on the deadlines adjustment to meet the

corresponding constraints and it presents a solution

for a more ﬂexible and relaxed system which can

react properly with its environment .

Notation:

Let us assume a reconﬁgurable system to be initially

composed of n periodic tasks T

,i = 1 . . . n. We

assume a reconﬁguration scenario to add m new

tasks. Each task is characterized by four parameters

according to (Liu and Layland, 1973). Firstly by its

release (or arrival) time r

, i.e each task T

cannot

begin execution before r

. Secondly by its absolute

deadline constraint d

, i.e. each task should ﬁnish

before d

. Thirdly by its computation time at the nor-

malized processor frequency C

. Finally by its period

which is equal to the deadline. It is assumed that the

WCET(Worst Case Execution Time) is constant and

that the tasks will be executed on a single processor

with a variable operating frequency according to

the EDF scheduling policy. We denote respectively

by f

and V

the normalized frequency and the

voltage of the system. the actual execution time

(i.e. computational delay) of the task is prolonged

when the voltage is decreased to save the energy.

The reason is that the frequency of the processor is

approximately linearly proportional to the supply

voltage(Zhu, 2005). We see that reducing voltage

cuts down the energy dissipation, but the operating

frequency will decrease accordingly. We can see that

the task execution time is inversely proportional to

the voltage. In order to provide the required system

performance, the supply voltage should be scaled as

low as possible to minimize the energy consumption,

while guaranteeing the temporal properties. We

suppose that each task T

is executed at frequency

and at voltage V

. We denote by η

the reduction

factor of voltage when T

is executed, V

. So the

WCET is equal to C

= C

.The power consumption

is P = CV

F where C is a constant related to the

circuit type of the processor ensuring that P

has

the dimension of a power(He et al., 2012). Hence,

if the system is running over x times, the energy

consumption is E = Px. The problem is then to

allow a low-power and real-time optimal scheduling

of reconﬁgurable tasks after each reconﬁguration

scenario. We assume a simpliﬁed model of power,

i.e. The power P

consumed by the task T

is :

= CV

= C

The energy E

consumed by the task T

is:

= P

= C

= K

with K = CV

So the total energy consumption of the system is:

E =

∑

i=1

= K

∑

i=1

(1)

the CPU charge factor U is calculated by:

U =

∑

i=1

(2)

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

where we remember that n denotes the number of

tasks in the system and C

, d

are respectively the ex-

ecution time and the deadline of the task i.

4 CONTRIBUTION: FLEXIBLE

RECONFIGURABLE

REAL-TIME SCHEDULING

WITH DEADLINE

ADJUSTMENT

This section deals with the proposed methods to com-

pute the scaling factor and estimate the deadline ad-

justment for the tasks after any reconﬁguration sce-

nario. The originality of our contribution consists in

ﬁnding not only the optimal scaling factors to ensure

temporal constraints but also the adjusted deadlines

which represent a ﬂexible proposed solution when the

processor drains all the available scaling factors and

the system lies unfeasible.

4.1 Mixed Integer Programming Model

The model tries to ﬁnd the optimal scaling factors and

minimize the total energy consumption of the system

under various operating constraints. We assume that

the tasks will be executed in a single processor sys-

tem with variable scaling factors. It is assumed that

the processor has a set of p available scaling factor.

we denote by m

: k = 1..p the k

available scaling

factors. We introduce a binary variable to describe the

combination between the scaling factor k and tasks i.







1 If the task i is executed with the scaling factor k

i = 1 ...n,k = 1 ... p

0 Otherwise

(3)

Let t

be the effective starting time of the task T

. Our

goal is to minimize the total consumed energy under

the following operating constraints:

a) No simultaneously executed tasks:

To ensure a single executed task in a time,

we should have either t

− t

− Cn

≥ 0

or t

− t

− Cn

≥ 0 or for every pair

of tasks T

and T

. This condition can be

rewritten as t

− t

≥ Cn

− Mα

i j

and

− t

≥ Cn

− M(1 − α

i j

) where α

i j

is a

binary variable and M is a big constant. α

i j

= 1

means that T

is executed before T

b) The deadline of each task should be respected

+Cn

≤ d

∀ k (4)

c) The the release time should be respected: t

≥

∀ i.

Thus the basic model is the following:











Minimize α

+ K

∑

i=1

s.t.

−t

≥ Cn

− Mα

i j

−t

≥ Cn

− M (1 − α

i j

)

αi (t

+Cn

i j

) ≤ d

∀ i

≥ r

∀ i

≤ 1

∑

i=1

≤ 1

∑

k=1

= 1 ∀ i

≥ 0 ∀ i

i j

∈ {0,1} ∀ i < j

(5)

With f

∑

k=1

) is the scaling factor of the

processor to execute the task i.

Case Study

We assume a real-time embedded system to be

composed of 5 tasks as depicted in table 1. The

Table 1: Current system conﬁguration.

Tasks Release time WCET deadline period

0 13 80 80

0 6 70 70

0 30 90 90

0 13 110 110

0 26 100 100

current system is feasible since the CPU charge is

equal to 0.959. The energy consumption is equal

to 2.112J = 2112mW . The CPU charge factor U

was calculated by equation (2) and the energy by

the equation (1) previously presented. We assume

a reconﬁguration scenario by adding 3 additional

tasks (table 2). The new system becomes infeasible

because the tasks (T

) miss their deadlines

and the CPU charge factor is equal to 1.327. The

energy consumption is also increased and becomes

2,952J = 2952mW .

The goal is to ensure that the feasibility of the

eight tasks while satisfying the energy constraints. So

AdaptiveEmbeddedSystems-NewComposedTechnicalSolutionsforFeasibleLow-PowerandReal-timeFlexibleOS

Tasks

Table 2: New system conﬁguration.

Tasks Release time WCET deadline period

0 13 80 80

0 6 70 70

0 30 90 90

0 13 110 110

0 26 100 100

0 10 85 85

0 11 94 94

0 14 105 105

Table 3: Applied model for WCET reconﬁguration.

Tasks WCET New

WCET

Start

time

Finish

time

Deadline Scaling

factor

13.00 10.40 0.00 10.40 80.00 0.80

6.00 4.80 10.40 15.20 70.00 0.80

39.00 31.20 36.20 67.40 90.00 0.80

13.00 10.40 99.60 110.00 110.00 0.80

26.00 20.80 15.20 36.00 100.00 0.80

10.00 10.00 67.40 77.40 85.00 1.00

11.00 11.00 77.40 88.40 94.00 1.00

14.00 11.20 88.40 99.60 105.00 0.80

Table 4: New system conﬁguration.

Tasks Release time WCET deadline period

0 73 80 80

0 65 70 70

0 83 90 90

0 103 110 110

0 96 100 100

0 75 85 85

0 81 94 94

0 100 105 105

we need to modify the scaling factor of the proces-

sor to ﬁnd an optimal combination for the execution

of the corresponding tasks. Our model was applied to

the system recently presented to resolve the problem.

It computes for each task, the start time, the ﬁnish

time, the scaling factor of the processor , the previ-

ous deadline, the new deadline and the new WCET

after changing the scaling factors. The results are pre-

sented in table 6. Now let us study the case when no

available scaling factor can fulﬁll the needs. We as-

sume that a reconﬁguration scenario has been applied

and the parameters of the tasks have been updated as

depicted in Table 4. Our model tries to adjust the

deadlines of tasks as a ﬂexible solution to meet the

corresponding requested constraints with a minimum

energy consumption. The model was solved with the

CPLEX solver Version 12.0. The computational re-

sults are shown in table 5.

4.2 Heuristic Approach

In this section, we present another method based

on heuristic optimization approach that aim to ﬁnd

Table 5: Applied model for WCET reconﬁguration.

Tasks WCET Start

time

Finish

time

scaling

factor

Last

dead-

line

New

dead-

line

New

WCET

73.00 95.40 110.00 0.2 80.00 119.80 14.60

65.00 53.20 79.20 0.4 70.00 104.80 26.00

83.00 00.00 33.20 0.4 90.00 134.80 33.20

103.00 144.20 164.80 0.2 110.00 164.80 20.60

96.00 125.00 144.20 0.2 100.00 149.80 19.20

75.00 110.00 125.00 0.2 85.00 125.30 15.00

81.00 79.20 95.40 0.2 94.00 140.80 16.20

100.00 33.20 53.20 0.2 105.00 157.3 20.00

the appropriate scaling factor and meet a feasible

system if possible, if not, the heuristic tries to adjust

the deadlines of the tasks so that all the temporal

constraints are respected without any energy lost.

The processor has a set of available operating speeds

such that each task can be executed with its own

speed.

Deﬁnition1:

Let S be a system of n periodic tasks. We denote

by V = (V

)

1≤i≤n

the vector of speeds where: V

the

execution speed of the task i.

Deﬁnition2:

Let A and B be two vectors of size n. We denote

A ≤ B (reads A is smaller than B) if A

≤ B

∀i.

Proposition1 :

Let V and V

be two vectors of speeds such as V ≤ V

If S is feasible with V then it is necessarily feasible

with V

Proof :

Let A be the feasible schedule of S under V that meets

the following three constraints:

• Release time r

of the task i,

• The worst execution time c

of the task i,

• The deadline d

of the task i.

A is also feasible under V

because ﬁrstly, S under

V and S under V

have the same release times and

secondly, the execution times of the tasks of S in

are smaller than those in V. We assume that the

processor has m levels of speeds V

< V

< · · · < V

We denote by V

max

= (V

,...,V

) the maximum

execution speed of all the tasks.

Proposition2 :

If S is not feasible under V

max

, then S is not feasible

under any speed. We assume that all the tasks are

activated at the time t = 0 i.e r

= 0∀i.

The heuristic is based on the following idea: ﬁrst, we

set a maximum speed for all the n tasks, if the system

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

is feasible (the CPU charge is equal or less than

1), we move to a lower speed and the operation is

repeated until the system becomes unfeasible. In this

case, the last value of the speed at which the system

is feasible is ﬁxed for the ﬁrst task and the procedure

is repeated with n − 1 remaining tasks. If the system

remains unfeasible (the CPU charge is greater than

1), the algorithm tries to increment the deadlines of

all the tasks and repeat the last process until reaching

the feasibility conditions.

Algorithm 1: Scheduling with deadline adjustment.

Inputs :

n number of tasks in the system

m Number of available levels of speed

Outputs :

A schedulable system

Begin :

repeat

V ← {V

,. .. ,V

}: set of available speeds

init

← {T

,. .. ,T

}: initial set of tasks

T ← T

init

Sort the tasks by increasing order of the priorities

i ← 1; j ← 1

while T is not empty do

repeat

Assign speed V

to all tasks in T

Compute the total charge U of the processor

Calculate the consumed energy E of the system

i ← i + 1

until (U > 1

if (i > 2) then

Assign V

i−2

to T

i ← i − 1

T ← T /{T

}

j ← j + 1

else

System can not be schedulable

T ←

end if

end while

Increase the deadline of all tasks

until (System is feasible)

End

Case Study

Let we have a processor with the following set of

scaling factor : {0.2,0.4,0.6,0.8,1} and the nominal

speed is equal to 1. The processor is charged to exe-

cute the following tasks (Table 6). The goal is to af-

fect the suitable processor speed to execute each task

in order to achieve a feasible system with low-power

energy consumption according to the proposed algo-

rithm. We compute in each iteration, the CPU charge

of the processor and the consumed energy. If the

available scaling factors of the processor cannot push

to a feasible system, the algorithm tries to change the

deadlines of the tasks as proposed solution.

Table 6: System conﬁguration.

Tasks Release time WCET deadline period

0 73 80 80

0 65 70 70

0 83 90 90

0 103 110 110

0 96 100 100

0 75 85 85

0 81 94 94

0 100 105 105

Iteration1: We affect the maximum speed V

= 5 for all

the assumed tasks (scaling factor=0.2).

5 5 5 5 5 5 5 5

(

110

100

105

) =

0.265 ≤ 1

I feasible system E

= 67.800mW

Iteration2: We affect the speed V

to all the

tasks : (scaling factor=0.4 ).

(

110

100

105

) =

0.530 ≤ 1 I feasible system E

= 16.950J

Iteration3: We affect the speed V

to all the

tasks: (scaling factor=0.6 ). V

for all task :

(

110

100

105

) =

0.769 ≤ 1

I feasible system

= 7.533J

Iteration4: We affect the speed V

to all the

tasks: (scaling factor=0.6).

(

110

100

105

) =

1.061 ≥ 1

I unfeasible system, I we allocate the speedV

to T

= 4.237J

AdaptiveEmbeddedSystems-NewComposedTechnicalSolutionsforFeasibleLow-PowerandReal-timeFlexibleOS

Tasks

Iteration5: We affect the speed V

to the tasks

,. .. ,T

}(scaling factor=0.8).

(

110

100

105

) =

1.029 ≥ 1

I unfeasible system, I we allocate speed V

to T

= 4.200J

Iteration6: We affect the speed V

to the tasks

,. .. ,T

}(scaling factor=0.8).

(

) +

(

110

100

105

) =

1.0119 ≥ 1

I unfeasible system, I we affect the speed V

to T

= 4.207J

Iteration7: We the affect speed V

to the tasks

,. .. ,T

}(scaling factor=0.8)

for tasks {T

,. .. ,T

}

(

) +

(

110

100

105

) =

0.945 ≤ 1

I feasible system, E

= 4.243J

Iteration8: We affect the speed V

= 1 to the tasks

,. .. ,T

}(scaling factor=1).

(

) + (

110

100

105

) =

1 1 1 1 1 1

1.095 ≥ 1

I system unfeasible, I we affects the speed V

to T

= 3.522J

Iteration9: We affect the speed V

= 1 to the tasks

,. .. ,T

}(scaling factor=1).

1 1 1 1

(

) +

110

+ (

100

105

) =

1.0713 ≥ 1

I system unfeasible, I we affect the speed V

to T

= 4.730J

Iteration10: We affect the speed V

= 1 to the tasks

,. .. ,T

}(scaling factor=1).

1 1 1

(

110

100

)+(

105

) =

1.0193 ≥ 1

I unfeasible system, I we affect the speed V

to T

= 4.745J

Iteration11 : We affect the speed V

= 1 to the tasks

,. .. ,T

}(scaling factor=1).

1 1

(

110

100

)+(

105

) =

0.9958 ≤ 1

I feasible system, I we affect the speed V

= 1 to

andT

, E

= 4.710J. I Final solution:

1 1

Table 7: System conﬁguration.

Tasks WCET deadline period

18 100 100

5 NUMERICAL RESULTS

We note that the implemented approaches in this pa-

per to solve the problem of non feasibility of a recon-

ﬁgurable real-time embedded system, provides more

efﬁcient results compared to those in (Chetto and

Chetto, 1990; Dwivedi, 2012). Our models allow

to compute the scaling factor more than the execu-

tion sequence of tasks, the start and the ﬁnish time of

each task. Our approaches give also good results in

the case when no available scaling factor can fulﬁll

the system requirements. To compare our developed

approaches(Integer programming approaches IP and

Heuristic) to theme presented in (Chetto and Chetto,

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Table 8: Comparation between IP ,Heuristic and (Dwivedi, 2012) models for Deadline adjustment.

Last WCET New WCET Last Deadline New Deadline

Task IP & Heuristic & (Dwivedi, 2012) IP Heuristic (Dwivedi, 2012) IP & Heuristic & (Dwivedi, 2012) IP Heuristic (Dwivedi, 2012)

18 7.2 7.2 18 50 90 85 50

18 7.2 10.8 18 50 90 93 80

18 7.2 10.8 18 50 90 102 110

18 7.2 7.2 18 50 90 64 138

18 7.2 7.2 18 50 90 108 150

Table 9: Comparation between integer programming and Heuristic approach.

Heuristic approach Integer programming approach

basic system+added tasks Time Energy CPU charge Time Energy CPU charge

5+5 54ms 63.31 0,9853 2.77s 24.075 0,9776

15+5 68ms 121.78 0,8821 11.76s 43.74 0,9799

20+10 71ms 169.26 0,99703 34.11s 54.18 0,9991

30+10 56ms 257.72 0,9885 387.52s 63.19 0,9836

40+10 87ms 269.13 0,9867 1706.09s 153.04 0,9831

45+15 97ms 364.05 0,9714 1787.23s 168.17 0,9362

50+20 124ms 353.25 0,9809 1792.42s 167.11 0,8929

60+20 142ms 451.93 0,9794 1801.65s 163.68 0,9652

70+20 178ms 467.49 0,9744 1831.46s 239.24 0,9310

80+20 193ms 557.91 0,9827 1807.96s 315.62 0,9440

150+50 308ms 1181.43 0,9720 1973.39s 756,81 0,9915

250+50 742ms 1737.40 1 2051.71s 1244.15 0,8791

300+100 3s 2201.21 0,9251 2408.15s 1423.52 0,8636

1990; Dwivedi, 2012), we consider a period selection

with da deadline to be equal to the corresponding pe-

riod. The parameters of the task system are depicted

in Table 7: By applying our developed approaches to

this task system, we obtain the following results: Ta-

ble 8 shows that our approaches (IP and Heuristic)

give results better than works presented in (Dwivedi,

2012) according to the deadline adjustment. In fact,

the gap between the last deadlines and the new dead-

lines is less for our applied methods. In addition, our

approaches try to modify the WCET by acting on the

scaling factor of the processor. In our experimenta-

tion, we have also randomly generated instances with

10 to 400 jobs. The numerical results are depicted

in table 9. The ﬁrst column shows the size of the

problem i.e the number of jobs. The sub-column la-

beled ”time” indicates the running time in millisec-

onds for each method. The sub-column labeled ”En-

ergy” gives the total energy consumption. The sub-

column labeled ”CPU charge” gives the total charge

of the processor. For example in Table 9 line 1, for

a system composed of 10 tasks(5 initial tasks with

other 5 added after a reconﬁguration scenario) we ob-

tain 63.31J as a consumed energy and a CPU charge

equal to 0,9853 in a time of 54ms by using the heuris-

tic approach. According to the integer programming

approach, we obtain for the same OS tasks 24.075

as the consumed energy and a CPU charge equal to

0,9776 in a time of 2.77s. Table 9 shows that the

energy consumption result of the applied integer pro-

gram is lower than that of the heuristic. However for

the large size instances, the heuristic is much faster.

We conclude that the integer programming is more

efﬁcient for the small instances. Moreover the two

approaches guarantee that all the constraints are re-

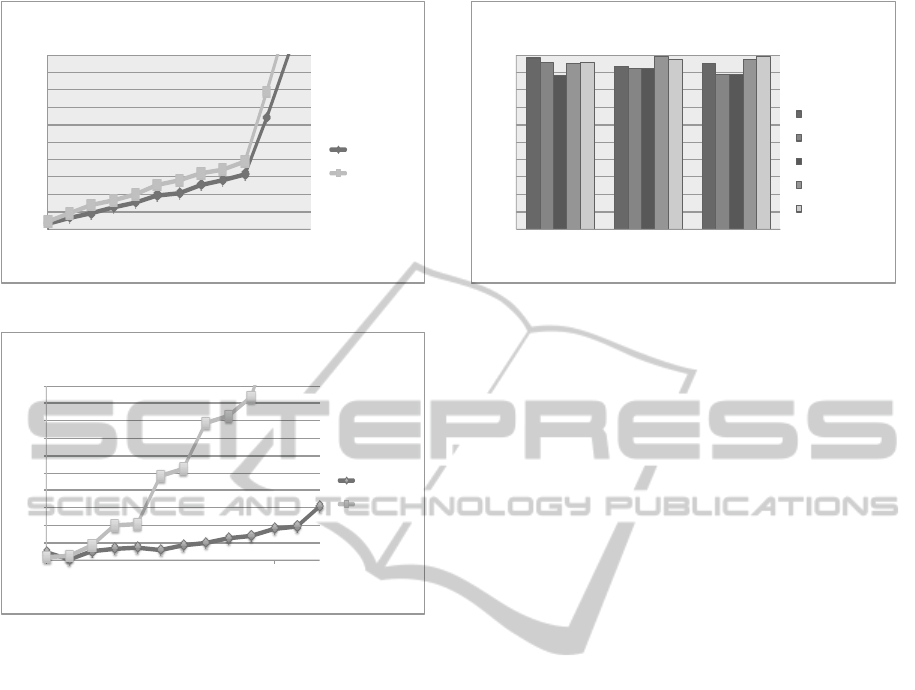
spected. Figures 1 and 2 present a graphic compa-

ration between the heuristic and the integer program-

ming in term of the CPU charge and the energy con-

sumption. According to the energy consumption, we

0,1"

0,2"

0,3"

0,4"

0,5"

0,6"

0,7"

0,8"

0,9"

5" 10" 15"

CPU$charge$

Size$of$problem$

Average$for$CPU$charge$$

integer"programming"*"

Heuris;c"method"*"

Constant"speed"step"

Descent"Cascade"

Simulated"annealing"

Figure 1: Comparation from CPU charge.

observe in Figure 2 that integer programming is more

effective as the number of instances increases because

it allows to explore more the search space of solutions

and can give a fairly optimal solution. We can observe

also that the heuristic is too fast than the integer pro-

gramming mainly for the large instances Figure 3. In

Figure 4, we compare the average CPU charge for the

AdaptiveEmbeddedSystems-NewComposedTechnicalSolutionsforFeasibleLow-PowerandReal-timeFlexibleOS

Tasks

200"

400"

600"

800"

1000"

1200"

1400"

1600"

1800"

2000"

10" 20" 30" 40" 50" 60" 70" 80" 90" 100" 200" 300" 400"

Energy'

Size'of'problem'

Energy'consump4on'

Integer"programming"

Heuris:c"method"

Figure 2: Comparation from energy consumption.

#!!"

$!!"

%!!"

&!!"

'!!"

(!!"

)!!"

*!!"

+!!"

#!!!"

#!" $!" %!" &!" '!" (!" )!" *!" +!" #!!" $!!" %!!" &!!"

Execu&on)&me))

Size)of)problem)

Execu&on)&me))

,-./0123"455/6437"

89:-;-/"5/6;/4<09;"

Figure 3: Comparation from energy consumption.

two proposed approaches and those presented as fol-

lows in (Jeannenot et al., 2004) on instances of 5 to

15 tasks. The solutions marked with ’*’ correspond

to our proposed approach in this paper, the rest refer

to (Jeannenot et al., 2004). The proposed models in

(Jeannenot et al., 2004) and(Chniter et al., 2014) try

to determine the correspondent scaling factors to en-

sure a feasible system, yet they they doesn’t take into

account the energy constraints, in addition, the pro-

posed model may not provide a solution in the case

where scaling factors do not allow a feasible system.

Our approaches try to exploit the ﬂexibility of the pro-

cessor to meet the new deadlines of tasks and to min-

imize the energy cost because in our contribution ap-

proaches will work in a reconﬁgurable real-time em-

bedded system so that the feasibility constraint after

a reconﬁguration scenario requires more resources of

processors.

6 CONCLUSIONS

In this paper, We have presented two combinato-

rial optimization approaches to solve the scheduling

0,1"

0,2"

0,3"

0,4"

0,5"

0,6"

0,7"

0,8"

0,9"

5" 10" 15"

CPU$charge$

Size$of$problem$

Average$for$CPU$charge$$

integer"programming"*"

Heuris;c"method"*"

Constant"speed"step"

Descent"Cascade"

Simulated"annealing"

Figure 4: Average CPU charge from each approach.

problem in a reconﬁgurable real-time embedded sys-

tem while minimizing the energy consumption. The

numerical results show that the integer programing

model provides more relevant results than the heuris-

tic approach. However, the heuristic is faster to exe-

cute large instances. Globally, the methods give more

chance to meet the timing requirements and overcome

the failure caused by the rejected tasks. As a fu-

ture work, our proposed models can be extended to

include other constraints such as multiprocessor sys-

tems and other criteria such as minimization of the

communication between the tasks and can include

other categories of tasks such as sporadic and aperi-

odic.

REFERENCES

Barr, M. (2007). ”embedded systems glossary”. Neutrino

Technical Library, 4(21).

Buttazzo, G. C., Lipari, G., and Abeni, L. (1998). Elastic

task model for adaptive rate control. RTSS, pages 286–

295.

Chantem, T., Hu, X. S., and Lemmon, M. D. (2009). Gen-

eralized elastic scheduling for real-time tasks. IEEE

Trans, Computers 58(4):480–495.

Chetto, H. and Chetto, M. (1990). A feasibility test for

scheduling tasks in a distributed hard real-time sys-

tem. APII, pages 239–25.

Chniter, H., Jarray, F., and Khalgui, M. (2014). Combinato-

rial approaches for low-power and real -time adaptive

reconﬁgurable embedded systems. International Con-

ference on Pervasive and Embedded Computing and

Communication Systems(PECCS).

cic¸ek, I. S. and Celik, C. (2011). Two meta-heuristics

for parallel processor scheduling with job splitting to

minimize total tardiness. Applied Mathematical Mod-

elling, 35(8).

Dalfard, V. M. and Mohammadi, G. (2012). Two meta-

heuristic algorithms for solving multi-objective ﬂex-

ible job-shop scheduling with parallel processor and

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

100

maintenance constraints. Computers & Mathematics

with Applications, 64(6):2111–2117.

Dwivedi, S. P. (2012). Adaptive scheduling in real-time

systems through period adjustment. CoRR abs/1212,

(3502).

Fang, K.-T. and Lin, B. M. T. (2013). Parallel-

processor scheduling to minimize tardiness penalty

and power cost. Computers & Industrial Engineering,

64(1):224–234.

Fidanova, S. (2006). Simulated annealing for grid schedul-

ing problem. In JVA ’06: Proceedings of the IEEE

John Vincent Atanasoff 2006 International Sympo-

sium on Modern Computing, pages 41–45.

He, C., Zhu, X., Hui Guo, A. Q., and Jiang, J. (2012).

Rolling-horizon scheduling for energy constrained

distributed real-time embedded systems. Journal of

Systems and Software, 85(4):780–794.

Heath and Steve (2003). Embedded systems design. EDN

series for design engineers (2 ed.), Newnes. p. 2.

ISBN 978-0-7506-5546-0.

Heilmann, R. (2003). A branch-and-bound procedure for

the multi-mode resource-constrained project schedul-

ing problem with minimum and maximum time

lags. European Journal of Operational Research,

144(2):348–365.

Hladik, P.-E., Cambazard, H., Deplanche, A.-M., and

Jussien, N. (2008). Solving a real-time allocation

problem with constraint programming. J. Syst. Softw,

81(1):132–149.

Imran Raﬁq Quadri, A. G., Boulet, P., Meftali, S., and

Dekeyser, J.-L. (2012). Expressing embedded sys-

tems conﬁgurations at high abstraction levels with uml

marte proﬁle: Advantages, limitations and alterna-

tives. Journal of Systems Architecture - Embedded

Systems Design, 58(5):178–194.

Jeannenot, S., RICHARD, P., and RIDOUARD, F. (2004).

Ordonnancement temps r

eel avec proﬁls variables de

consommation d’

energie. Real-Time Embedded Sys-

tems.

Letters, I. P., editor (1996). A note on scheduling on a sin-

gle processor with speed dependent on a number of

executed jobs, volume 297-300.

Liu, C. L. and Layland, J. W. (1973). Scheduling algo-

rithms for multiprogramming in a hard-real-time en-

vironment. J. ACM, 20(1):46–61.

Nossal, R. (1998). An evolutionary approach to multipro-

cessor scheduling of dependent tasks. In 1st Interna-

tional Workshop on Biologically Scheduling of Depen-

dent Tasks, Orlando, Florida, USA.

PARAIN, F., BANATRE, M., CABILIIC, G., HIGUERA,

T., ISSARNY, V., and LSEOT, J. (2000). Tenchiques

de r

eduction de la consommation dans les syst

emes

embarqu

es temps r

eel. INRIA Research report,

(3932).

Xu, R. (1993). Multiprocessor scheduling of processes with

release times, deadlines, precedence, and exclusion

relations. EEE Transactions, 19(2).

Ying, K.-C. and Cheng, H.-M. (2010). Dynamic parallel

processor scheduling with sequence-dependent setup

times using an iterated greedy heuristic. Expert Syst.

Appl, 37(4):2848–2852.

Zhu, Y. (2005). Dynamic voltage scaling with feedback edf

scheduling for real-time embedded systems. Master’s

thesis, North Carolina State University.

AdaptiveEmbeddedSystems-NewComposedTechnicalSolutionsforFeasibleLow-PowerandReal-timeFlexibleOS

Tasks

101