
Dynamical Model of Asphalt-Roller Interaction During Compaction
Syed Asif Imran
1
, Fares Beainy
2
, Sesh Commuri
1
and Musharraf Zaman
3
1
School of Electrical and Computer Enginnering, University of Oklahoma, W. Boyd St, Norman, Oklahoma, U.S.A.
2
Volvo Construction Equipment, Volvo Way, Shippensburg, Pennsylvania U.S.A.
3
School of Civil Enginnering and Environmental Science, University of Oklahoma, W. Boyd St, Norman, Oklahoma, U.S.A.
Keywords: Intelligent Compaction, Vibration Analysis, Asphalt Pavements, Roller Dynamics, Construction
Engineering.
Abstract: Proper and uniform compaction during construction is of utmost importance for the long term performance
of asphalt pavement. Variations in the conditions of freshly laid pavements require adjustment of the
compaction effort in order to obtain uniform and adequate density. One of the goals of on-going research in
Intelligent Compaction (IC) is the development of adaptive feedback control mechanism to adjust the
compaction effort according to the field and pavement conditions. Such feedback control systems require a
good understanding of compaction dynamics. In this study, a dynamical model is developed to study the
interaction between a moving vibratory roller and the underlying asphalt pavement during compaction. The
asphalt pavement is represented as a lumped element model with visco-elastic-plastic properties. A
procedure is presented to estimate the parameters of this model from standard tests on asphalt mix
conducted in the laboratory. The combined roller-pavement dynamical model is used to replicate field
compaction of an asphalt pavement using a vibratory roller. Numerical simulation results indicate good
agreement with results observed during compaction of pavements in the field. Comparison between the
simulation results and the results collected from the actual pavement construction job show that the model
could be used as a mathematical basis for the development of advanced compaction methods.
1 INTRODUCTION
Compaction is one of the important steps in
pavement construction that affect the quality of
asphalt pavement. Proper compaction increases the
load bearing capacity of the pavement and provides
a smooth riding surface. It also increases the useful
life of a pavement by reducing its susceptibility to
early failure due to fatigue, rutting, low temperature
cracking and aging (US Army Corps, 2000). The
construction of an asphalt pavement begins with the
preparation of the base and subsequent laydown of
asphalt mix of desired thickness. Rollers with
rotating eccentric masses in the drum are then used
to impart static and vibratory energy to the asphalt
mat to reduce the air voids and improve the stiffness
of the pavement. Several factors like the
composition of asphalt mix, its temperature at
laydown, thickness of the layer, temperature and
stiffness of the underlying layer, temperature,
velocity and humidity of air, and solar radiation
levels affect the compactbility of asphalt mix
(Brown et al., 2009). Unless these factors are
addressed during the construction process, they can
lead to non-uniform compaction of the pavement.
Intelligent Compaction (IC) technologies are being
developed to provide continuous real-time quality
control by monitoring the level of compaction of the
pavement and adjusting the amount of compaction
energy applied by the roller in order to obtain
uniform stiffness/density.
One of the goals of IC is to develop an automatic
feedback control system that can take into account
compaction quality and modify in real time, roller
parameters such as speed, frequency and amplitude
of vibration, to improve the overall quality of the
construction (Chang et al., 2012). Intelligent
Compaction is based on the hypothesis that the
vibratory roller and the underlying pavement layers
form a coupled system. The response of the roller is
determined by the frequency of its vibratory motors
and the natural vibratory modes of the coupled
system (Imran et al, 2012). Compaction of the
pavement increases its stiffness and as a result, the
vibrations of the compactor are altered. The
559
Imran S., Beainy F., Commuri S. and Zaman M..
Dynamical Model of Asphalt-Roller Interaction During Compaction.
DOI: 10.5220/0005066905590567
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 559-567
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

knowledge of the field conditions and the vibration
spectra of the compactor can, therefore, be used to
estimate the properties of the pavement layer
(Beainy et al., 2012, Commuri et al., 2009, Commuri
and Zaman, 2010, Commuri, 2012). A feedback
controller can utilize these estimated properties to
adjust the amount of compaction energy applied at
any given location on the pavement. These
adjustments are designed to ensure that the energy is
applied only to those areas of the pavement that are
under-compacted while avoiding over-compaction
of areas that are adequately compacted. Such a
process is expected to improve the uniformity of
density/stiffness of the pavement over its entirety
and increase its useful life.
Development and analysis of an IC feedback
control system requires a good understanding of the
interaction of the roller and asphalt pavement and a
model that can accurately represent the dynamics of
the coupled system. The model has to account for
factors such as temperature, density, and thickness
of the pavement and loading frequency of the roller
that affect the dynamics of the coupled system.
Since these factors can change during the course of
the compaction process, the model should adapt to
these changes.
In recent years, attempts have been made to
develop numerical techniques and analytical models
to examine the response of asphalt mixes during
compaction. Lodewikus (Lodewikus, 2004)
developed a Finite Element Method (FEM) approach
based on critical state theory to analyze the behavior
of asphalt mix. Masad et al. (Masad et al., 2010)
developed a thermodynamics-based nonlinear
viscoelastic model for capturing the response of
asphalt mix during compaction. Pei-Hui Shen and
Shu-Wen Lin (Shen and Lin, 2008) derived an
asymmetrical model of hysteresis based on the
classical Bouc-Wen hysteresis model to investigate
the dynamic characteristics of a vibratory
compaction system.
Researchers have utilized analytical models such
as Maxwell, generalized Maxwell, Kelvin–Voigt,
generalized Kelvin, Huet–Sayegh, and Burger
models to represent the asphalt pavement as a
combination of springs and dampers (Nillson et al.,
2002; Pronk, 2005; Dave et al., 2006; Xu and
Solaimanian, 2009). These models were mostly used
to study the long term behavior of the pavement
under traffic loads. Their applicability in
representing the pavement during field compaction
is not widely studied. Among the analytical models,
Burger’s model is simple and can accurately
describe the viscoelastic behavior of an asphalt
pavement (Liu and You, 2009; Liu et al., 2009).
Beainy et al. (2013a, 2013b) showed that Burger’s
model can be used to develop a Visco-Elastic-Plastic
model that can represent the dynamical properties of
asphalt pavement during compaction.
Although Beainy’s model provides a good
insight into the compaction dynamics, it does not
consider the longitudinal and lateral movement of
the roller. Only the interaction between the drum and
the asphalt mat in the vertical direction is taken into
acount. However, during compaction, the roller
moves at a speed of 4-7 km/h along the pavement as
it compacts the mix. Therefore, there is a spatial
separation between each impact. In this research,
Beiany’s visco-elastic-plastic model is enhanced to
incorporate the effect of spatial movement of the
roller. A mathematical model is developed to
describe the asphalt-roller interaction as the roller
traverses the pavement using a conventional rolling
pattern. Simulation is performed to obtain the
density profile for the asphalt pavement after a
traditional compaction is complete. Simulation
results show that the model can be used to
understand the dynamics of field compaction and to
represent the densification achieved during field
compaction. This understanding will be useful in
studying the performance of different types of
asphalt mixes and in developing techniques for
improving the quality of constructed pavements.
The rest of the paper is organized as follows. The
development of the dynamics of the coupled system
is detailed in Section 2. A method to determine the
parameters of the model based on experimental
results from standard laboratory tests is discussed in
Section 3. Verification of the proposed approach
through numerical simulations is presented in
Section 4 and the conclusions and scope of future
work are discussed in Section 5.
2 DEVELOPMENT OF THE
MODEL
The model developed for this research is an
extension of Beainy’s model (Beainy et al, 2013a,
Beainy et al., 2013b) which is based on the
assumption that the roller and the underlying
pavement form a coupled system during compaction.
Therefore any changes in the stiffness of the asphalt
pavement would affect the vibration of the drum of
the roller. The roller uses both the static force
(weight of the drum and frame) and an impact force
to compact the asphalt material. The impact force is
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
560

a result of an eccentric mass rotating around the axle
of the drum. It can be expressed as
sin
sin
2
(1)
Where,
is the moment of the eccentric
mass and
is the angular frequency of rotation.
It should be noted that only the movement of the
drum in vertical direction is considered in the
derivation of the model. The coupling between the
drum and the frame of the roller is modelled as a
parallel combination of a spring and a dashpot. The
spring elements follow Hooke’s law (; where
is the applied stress, is the resulting strain and
is the Young’s modulus of the spring). The dashpot
elements are assumed to follow the Newton’s law (
, where ‘’ is the applied stress, ‘’ is the
strain and ‘’ is the viscosity).
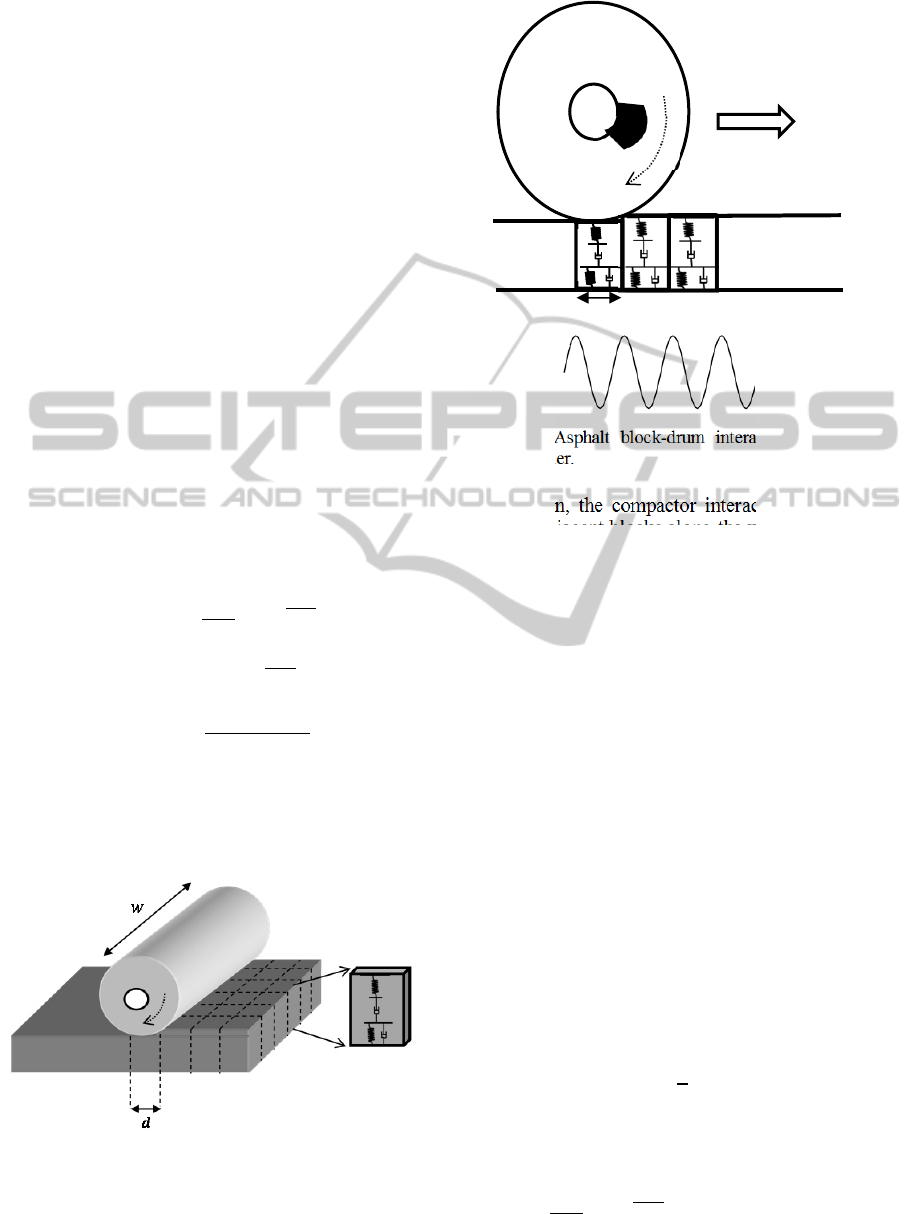
The underlying asphalt pavement is modelled as
a collection of blocks of Burger’s material arranged
in a grid. Burger’s material can be represented by a
series combination of a spring representing the of
spring and dashpot representing the delayed
(viscous) response, and a dashpot that represents the
permanent deformation (Figure 1). It is considered
that at any given time the roller drum interacts with
adjacent blocks of equal width that are in contact
with the drum. The reaction force of the pavement to
the drum is the sum of the force exerted by each of
the blocks. In the development presented in this
paper, the asphalt pavement is considered to be laid
on top of a rigid base.
The total deformation occurring in th block of the
asphalt pavement due to stress applied by the roller
is comprised of an instantaneous elastic deformation
‘
’, a delayed viscous deformation ‘
’, and a
permanent deformation ‘
’. The constitutive
equation of the strain can be expressed as
1
(2)
where
is the force experienced by the th block.
The viscous property of the block is represented as
using a spring of stiffness
and a dashpot of
damping
. The elastic strain is represented by the
displacement of a spring of stiffness
and the
permanent deformation is modelled as a dashpot of
coefficient
for th block.
, and
are
constants that represent the boundary conditions
(Beainy et al, 2013a, Beainy et al., 2013b).
The dynamics of interaction between the roller
and the asphalt mat can be formulated as
Figure 1: Viscoelastic-plastic model of asphalt-roller interaction.
Ri
g
id
Viscous
ε
(
t
)
Instantaneous
Permanen
t
Asphalt
DynamicalModelofAsphalt-RollerInteractionDuringCompaction
561
sin
(3)
(4)
(5)
where
is the displacement of the asphalt layer;
is the reaction force of the asphalt layer;
is the
drum-asphalt contact force;
is the displacement
of the drum;
is the displacement of the frame;
is the drum-frame stiffness coefficient;
is the
velocity of the drum;
is the velocity of the frame;
is the drum-frame damping coefficient;
is
the asphalt weight;
is the vertical acceleration of
the drum;
is the vertical acceleration of the
asphalt pavement;
is the acceleration of the frame.
The reaction force of the asphalt mat
can be
expressed as
1
(6)
For simplicity of calculation, the drum is
considered to be in constant contact with the asphalt
mat. The bouncing of the drum due to excessive
vibrations is being studied in on-going research.
Figure 2: Block representation of asphalt pavement.
In this study, the pavement is considered as a
grid of small blocks. At each impact during
Figure 3: Asphalt block-drum interaction model for a
moving roller.
compaction, the compactor interacts with only one
set of 6 adjacent blocks along the width of the drum.
The size of each block is dependent on the geometry
of the drum and asphalt layer, the velocity of the
roller and the frequency of the vibration. Its height is
equal to the thickness of the pavement layer. The
width corresponds to 1/6 th of the width of the drum.
The length is the distance the roller travels along the
pavement while making one impact. At the
beginning of each impact cycle the drum moves on
top of a new set of blocks. The interaction between
the roller and each set of block continues for one
cycle of the vibration. Then in the next cycle the
roller moves to the next block set. The parameter
values of each block are dependent on the density
and temperature of the block.
During the first pass of the roller each grid
element representing the pavement is assumed have
no initial permanent or visco-elastic deformation.
The elastic deformation comes into play the moment
the roller drum comes into contact with the grid
element. Therefore,
0
(7)
1
6
(8)
Using these boundary conditions, the constants
and
can be determined. Setting
1
0
(9)
Roller
Vibration
Direction
of Roller
Motion
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
562

Similarly, setting
0
.
(10)
Where,
is the time at which the drum starts
compacting the nth block of the stretch.
However, from the second pass of the roller, the
constant
of each block is equal to the resultant
permanent deformation after the previous pass. The
viscous deformation is considered to be recovered
between consecutive passes. Therefore
is
calculated in the same manner for all the passes.
3 DETERMINATION OF MODEL
PARAMETERS
3.1 Roller Parameters
Roller parameters include mass of the drum, mass of
the frame, drum-asphalt contact area, width and
diameter of the drum, stiffness coefficient and
damping coefficient of drum-frame, rotational
frequency of eccentrics and the eccentric moment.
These parameters can be determined from the
manufacturer’s specifications of the roller. The IR
DD 118HF vibratory compactor is considered in this
study in order to illustrate the procedure.
The drum-asphalt contact area is dependent on
the drum width, weight of the compactor, stiffness
of asphalt pavement, and total eccentric force
applied to the pavement (Kröber et al. 2001).
However, in this study, since the roller is assumed to
be interacting with only 6 blocks that are underneath
the drum for any given cycle period. The total
contact force is assumed to be evenly distributed in
the whole surface area of the block. The contact area
is also assumed to be equal to the surface area of the
blocks. The contact area between the drum and each
block is calculated according to the following
equation,
/6
(11)
where,
is the drum-asphalt block contact area,
is the length of the block underneath and is the
width of the drum. The mass of the blocks in contact
with the roller can then be determined using the
contact area and the thickness of the pavement layer
as well as the asphalt mix properties.
3.2 Pavement Parameters
Liu et al. (2009) developed a procedure to determine
Burger’s model parameters by fitting the parameters
with the complex modulus test data. This procedure
is enhanced to estimate the four parameters
(
,
,
, and
) of the asphalt pavement
section of the model (Beainy et al., 2013a, Beainy et
al., 2013b). A laboratory testing according to
AASHTO TP-62 standard procedure (AASHTO
2007) is first performed to determine the dynamic
modulus |E* | and the phase angle ϕ of the asphalt
mix at different temperatures, air void contents, and
loading frequencies. The relationship between the
dynamic modulus and phase angle of the mix and
the model parameters can be expressed as follows
1
∗
1
1
12
(12)
tan
1
tan
(13)
lim
⟶
|
∗
|
(14)
and
lim
⟶
|
∗
|
(15)
An iterative procedure is adopted to determine
the model parameter values at the different loading
frequencies and temperature values used in
laboratory testing. The procedure is shown in the
flow chart (Figure 4) where
,
are the
maximum and minimum values of angular
frequencies in laboratory tests.
The parameters
,
,
, and
are
obtained for different test loading frequencies and
temperatures. These values are then extrapolated
using a power curve fitting method to get estimated
values at operating frequency of the roller. The
pavement properties such as temperature () and air
void content (
) of the mix vary during compaction.
DynamicalModelofAsphalt-RollerInteractionDuringCompaction
563
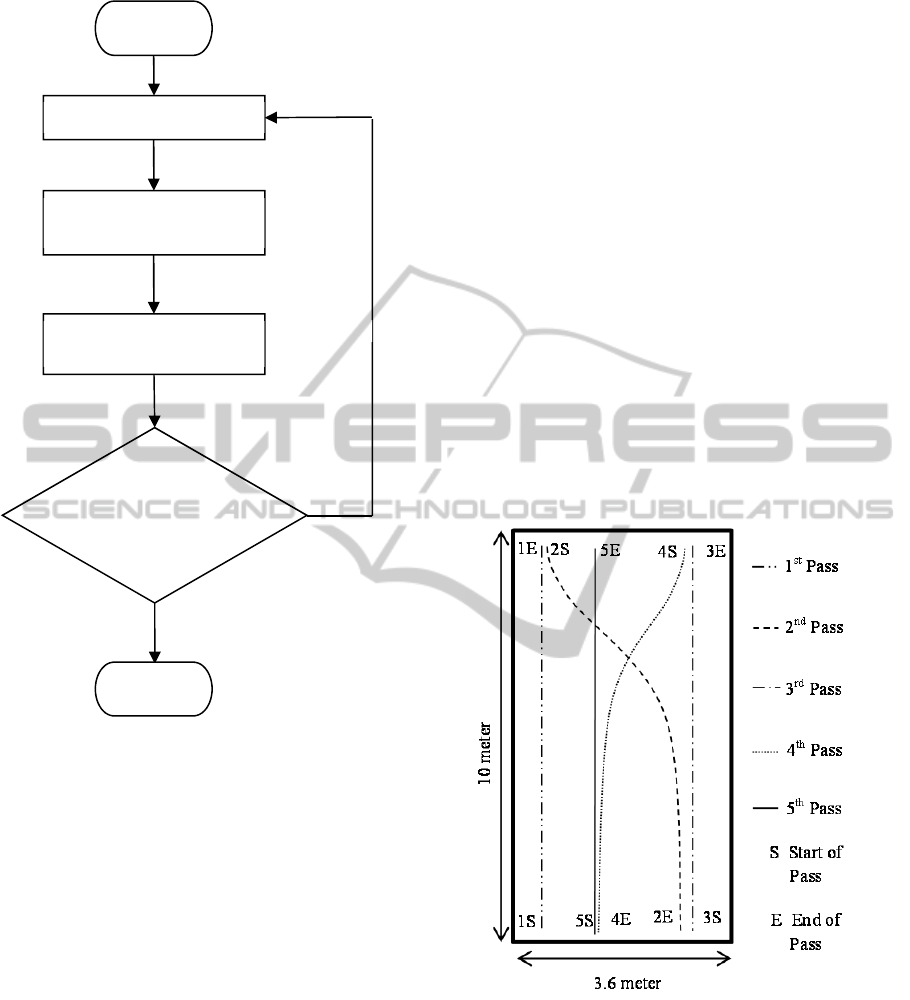
Figure 4: Flow chart of the iteration process to determine
the Burger’s model parameters.
This affects the stiffness and viscosity of the
pavement. Equations are developed to estimate the
parameter values taking into account the pavement
temperature and air void content. These are
expressed as follows.
534084
5428.5
0.23
0.31
0
0.15
0.0085
0.00054
(16)
71291373
125.1106.9
5.1
0.831
0
0.5673
0.01493
0.001496
(17)
4088384.4
41.5312.7
2.677
0.1767
0
0.0657
0.00446
0.0002987
(18)
349.487.32
0.96647.825
0.0933
0.003178
0.2273
0.003858
0.000065
0.0000056
(19)
4 NUMERICAL SIMULATION
Simulation is performed to study and evaluate the
response of the model. The physical model includes
an IR DD 118HF smooth drum vibratory roller
compacting a 76.2 mm thick layer of asphalt mix
with a nominal maximum aggregate size of 12.5mm
and PG 76 -28 binder. The roller is assumed to
operate at rated frequency of 50 Hz and moving at a
constant speed of 6.4km/h throughout the process.
The parameters of the grid elements representing the
asphalt pavement are varied with the variation of
operating frequency of the roller, and the
temperature and density of the mix. The parameter
values are calculated using the set of equations (Eq
16-19) discussed in the previous section. During
simulation, the model continuously monitors the
roller operating frequency, temperature and air void
contents of the pavement for each block and adjusts
its parameter values accordingly. The roller is
assumed to be initially at rest and in contact with the
asphalt mix.
Figure 5: Rolling passes performed by the roller.
Simulations are performed for 5 consecutive
passes of the roller using a conventional rolling
pattern on the compaction stretch. The pavement is
considered to be 10 meter long and 3.6 meter wide.
The rolling pattern is shown in Figure 5. Since the
drum width is 2 meters, there is some overlap
between adjacent passes as the roller moves back
and forth while executing the rolling pattern.
Therefore, some grid elements representing the
Yes
Start
Adjust
and
Calculate
and
for
all test fre
q
uencies
Are
>0
and
>0for
all test
Estimate
and
for
the new
and
End
No
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
564
pavement are compacted with only one pass while
other regions are compacted during each roller pass.
In the simulation examples presented, the
temperature of the asphalt mix at laydown is
considered to be 150
0
C and the material is assumed
to comprise of 12% air voids over the entire stretch.
This is done in order to replicate conditions
commonly encountered in the field. Therefore, the
parameter values are same for each block at
laydown. After simulation of each roller pass, the
model parameters of each grid element is stored and
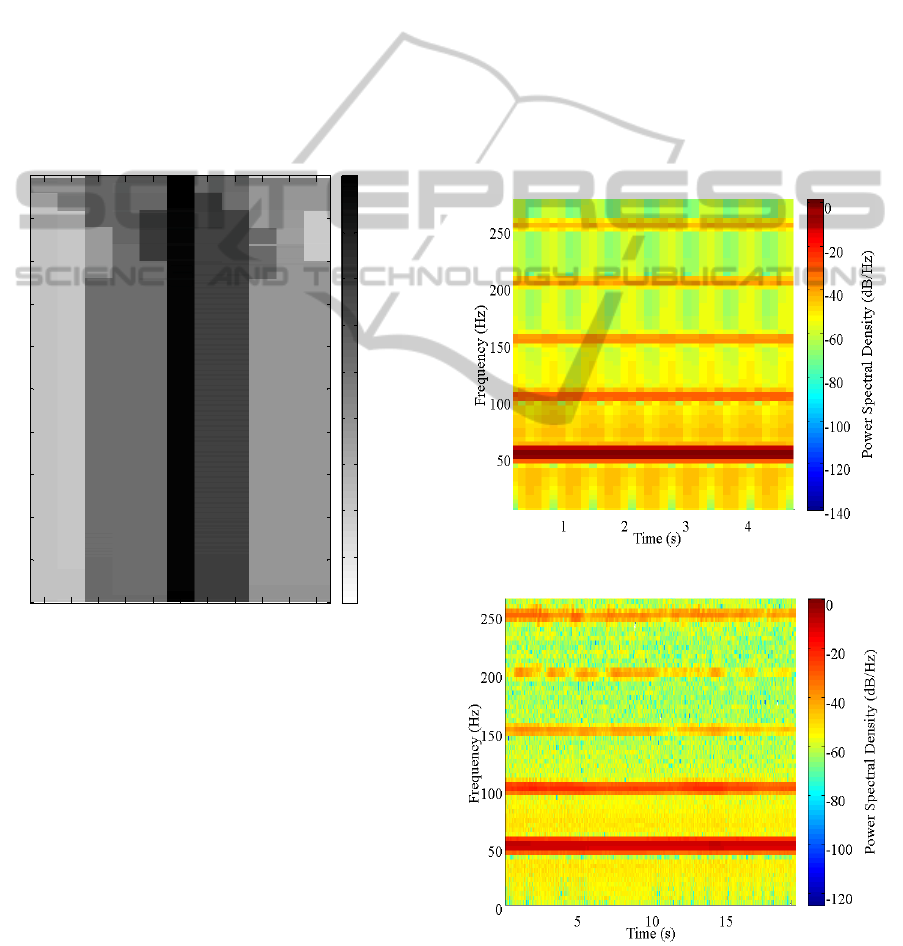
used as initial condition for the next pass. Figure 6
shows the density profile of the pavement after the
compaction of the roller. In this figure, darker
shading indicates higher density (represented as a
percentage of maximum theoretical density) of the
pavement.
Figure 6: Density profile of the pavement after rolling
passes.
From simulation results (Figure 6) it can be seen
that up to 2% variability in density is possible
between locations a few inches apart on the
pavement. Previous field investigation performed by
researchers at the University of Oklahoma (Beainy
et al., 2011) on interstate I 86 near Hornell, New
York also observed variability in density for up to
1.8% between cores with spatial distance of just a
few inches.
Results of the simulations of the model are
compared with actual data collected during the
construction of Interstate I-35 in Norman, Oklahoma
using a IR DD 118HF vibratory compactor. The
vibrations of the roller were captured using a
13,200C uniaxial accelerometer from Summit
Instruments is mounted on the axle of the drum.
These vibrations were recorded during compaction
of a 50.8 mm thick asphalt pavement comprising of
a 12.5 mm PG 76 -28 OK Superpave asphalt
mixture. Model parameters were determined for this
asphalt mix and used to simulate the compaction in
the field. The spectrogram of the vibrations obtained
using numerical simulations is shown in Figure 7.
Figure 8 shows the spectrogram of the vibrations of
the roller observed during field compaction. In these
figures, the normalized power in each frequency
band is depicted using a color coded map. It is
evident that the model presented in this paper
captures not only the response of the roller at the
fundamental frequency (frequency of the eccentrics),
but also the response at the harmonics.
Figure 7: Simulated roller vibration spectrum.
Figure 8: Measured roller vibration spectrum.
Pavement Width (meter)
Pavem ent Length (m eter)
0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4 2.7 3.0 3.3
9
8
7
6
5
4
3
2
1
0
Density (% )
88
88.5
89
89.5
90
90.5
91
91.5
92
92.5
DynamicalModelofAsphalt-RollerInteractionDuringCompaction
565

5 CONCLUSIONS
The development and validation of a dynamical
model that can emulate the field compaction of
asphalt mixes during construction of asphalt
pavements was presented in this paper. A method to
determine the parameters of the model using
laboratory test data and roller information was
developed and the use of this model in replication
field compaction was studied. The model was
developed using established visco-elastic-plastic
representation of asphalt mixes and for the first time,
extended such modelling to the study of field
compaction of asphalt pavements.
Numerical simulations show that this approach
captures the compaction process well and can be
used to study the performance of different type of
mixes used for the construction of asphalt
pavements. The approach presented in this paper is a
first step towards the development and testing of
closed-loop techniques for intelligent compaction of
pavements.
The model used in this paper was derived
assuming rigid base, fixed contact area between
roller drum and asphalt pavement, and constant
speed of the roller during compaction. The effects of
shear flow of asphalt as well as the effects of
confinement at the edges were also not considered.
Future research is aimed at relaxing these
assumptions.
REFERENCES
American Association of State Highway and
Transportation Officials. 2007. Standard Method for
Determining Dynamic Modulus of Hot-Mix Asphalt
Concrete Mixtures: TP 62-03. AASHTO Provisional
Standards.
Beainy, F., Commuri, S., and Zaman, M. 2010. Asphalt
compaction quality control using artificial neural
network. 49th IEEE Conference on Decision and
Control (CDC), 4643-4648.
Beainy, F., Commuri, S., and Zaman, M. 2011. Quality
assurance of hot mix asphalt pavements using the
intelligent asphalt compaction analyser. ASCE Journal
of Construction Engineering and Management,
138(2), 178-187.
Beainy, F. 2011. Non-contact sensor for the real-time
measurement of stiffness of asphalt pavements during
compaction. Ph.D. Dissertation, The University of
Oklahoma.
Beainy, F., Commuri, S., Zaman, M., & Imran, S. 2013a.
Viscoelastic-Plastic Model of Asphalt-Roller
Interaction. ASCE International Journal of
Geomechanics, 13(5), 581-594.
Beainy, F., Commuri, S., and Zaman, M. 2013b.
Dynamical Response of Vibratory Rollers during the
Compaction of Asphalt Pavements. ASCE Journal of
Engineering Mechanics. Published online, 16 October
2013.
Brown, E., Kandhal, P. S., Roberts, F. L., Kim, Y., Lee,
D., and Kennedy, T. 2009. Hot Mix Asphalt Materials,
Mixture Design, and Construction. Third Edition,
NAPA Research and Education Foundation, 60, 321-
384, 459.
Chang, G., Xu, Q., Horan, B., and Michael, L. 2010.
Accelerated Implementation of Intelligent Compaction
Technology for Embankment Subgrade Soils,
Aggregate Base, and Asphalt Pavement Materials -
Final Report for the PennDOT HMA IC
Demonstration. Report FHWA-IF-07, Federal
Highway Administration, Washington, D.C.
Commuri, S., Mai, A.T., and Zaman, M. 2009. Calibration
Procedures for the Intelligent Asphalt Compaction
Analyzer. ASTM Journal of Testing and Evaluation,
37(5), 454-462.
Commuri, S., and Zaman, M. 2010. Method and apparatus
for predicting the density of asphalt. USPTO,
7,669,458, March 02, 2010.
Commuri, S. 2012. Method and apparatus for compaction
of roadway materials. USPTO, Patent 8,190,338 B2,
May 29, 2012.
Corps of Engineers. 2000. Hot-Mix Asphalt Paving
Handbook 2000. AC 150/5370-14A, US Army Corps
of Engineers, Washington, D.C.
Dave, E., Buttlar, W., Paulino, G., and Hilton, H. 2006.
Graded Viscoelastic Approach for Modeling Asphalt
Concrete Pavements. International Conference FGM
IX, American Institute of Physics, 736-741, Oahu
Island, Hawaii.
Imran, S., Beainy, F., Commuri, S., and Zaman, M. 2012.
Transient response of a vibratory roller during
compaction. IEEE 51st Annual Conference on
Decision and Control (CDC), 4378-4383.
Kröber, W., Floss, R., and Wallrath, W. 2001. Dynamic
soil stiffness as quality criterion for soil compaction.
Geotechnics for roads, rail tracks, and earth structures,
Balkema, Lisse, Netherlands.
Lodewikus, H. 2004. Compaction of asphalt road
pavements: using finite elements and critical state
theory. PhD Dissertation. University of Twente,
Enschede, Netherlands.
Liu, Y., and You, Z. 2009. Determining Burger’s Model
Parameters of Asphalt Materials using Creep-recovery
Testing Data. Pavements and Materials: Modeling,
Testing, and Performance. ASCE Geotechnical
Special Publication, 184, 26-36.
Masad, E., Koneru, S., Scarpas, T., Kassem, E., and
Rajagopal, K. 2010. Modeling of Hot-Mix Asphalt
Compaction: A Thermodynamics-Based Compressible
Viscoelastic Model. Texas Transportation Institute,
Office of Acquisition Management, Federal Highway
Administration, Washington, D.C.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
566

Nillson, R., Hopman, P., and Isacsson, U. 2002. Influence
of different rheological models on predicted pavement
responses in flexible pavements. Road Materials and
Pavement Design: An International Journal, 3, 117-
149.
Pronk, A. 2005. The Huet–Sayegh model: a simple and
excellent rheological model for master curves of
asphaltic mixes. Lytton Symposium on Mechanics of
Flexible Pavements, Baton Rouge, LA.
Shen, P. H., and Lin, S. W. 2008. Mathematic modeling
and characteristic analysis for dynamic system with
asymmetrical hysteresis in vibratory compaction.
Meccanica, 43(5), 505-515.
Xu, Q., and Solaimanian, M. 2009. Modelling linear
viscoelastic properties of asphaltconcrete by the Huet–
Sayegh model. International Journal of Pavement
Engineering, Taylor & Francis, 10(6), 401-422.
DynamicalModelofAsphalt-RollerInteractionDuringCompaction
567
