Evaluation of Acoustic Feedback Cancellation

Methods with Multiple Feedback Paths

B. C. Bispo and D. R. Freitas

Department of Electrical and Computer Engineering, University of Porto, Porto, Portugal

Keywords:

Public Address System, Acoustic Feedback Cancellation, Evaluation, Multiple Feedback Paths.

Abstract:

Acoustic feedback limits the maximum stable gain of a public address system and may cause the system to be-

come unstable. Acoustic feedback cancellation methods use an adaptive ﬁlter to identify the impulse response

of the acoustic feedback path and then remove its inﬂuence from the system. However, if the traditional adap-

tive ﬁltering algorithms are used, a bias is introduced in the estimate of the acoustic feedback path obtained by

the adaptive ﬁlter. Several methods have been proposed to overcome the bias problem but they are generally

evaluated considering a public address system with only one microphone and one loudspeaker. This work

evaluates some of the state-of-art methods considering a public address system with one microphone and four

loudspeakers that results in multiple feedback paths and corresponds to a more realistic scenario of a typical

system. Simulation results demonstrated that, with multiple feedback paths, the acoustic feedback cancellation

methods are able to increase in 12 dB the maximum stable gain of the public address system when the source

signal is speech.

1 INTRODUCTION

In a typical public address (PA) system, a speaker uses

loudspeakers and microphones along with an ampliﬁ-

cation system to apply a gain on his/her voice signal,

aiming to be heard by a large amount of people in

the same acoustic environment. The speaker’s speech

signal v(n), after being picked up by the micro-

phones, ampliﬁed and played back by the loudspeak-

ers, may return to the microphones going through sev-

eral paths. Such a system is illustrated in Fig. 1 with,

as usual, only one microphone and one loudspeaker.

Forward Feedback

PathPath

P P

u(n) v(n)

r(n)

x(n)

y(n)

G(z, n) F (z, n)

Figure 1: Acoustic feedback in a PA system.

Among these paths are included the direct one, if

it exists, as well as the ones given by a large num-

ber of reﬂections. In all cases there is some signal

attenuation which becomes more intense with the in-

crease in length and therefore only a ﬁnite number

of reﬂections can be considered in the feedback path.

For simplicity, the feedback path also includes the

characteristics of the D/A converter, loudspeaker, mi-

crophone and A/D converter. Although some non-

linearities may occur due to saturation of the loud-

speaker, almost invariably it is considered that these

devices have unit responses and that the feedback path

is linear. Hence, the acoustic feedback path is usually

deﬁned as a ﬁnite impulse response (FIR) ﬁlter

F(z,n) = f

(n) + f

(n)z

−1

+ . .. + f

−1

(n)z

−(L

−1)

= [ f

(n) f

(n) ... f

−1

(n)]





−1

−(L

−1)





= f

(n)z (1)

with length L

The forward path includes the characteristics of

the ampliﬁer as well as of any other signal processing

device inserted in the signal loop, such as an equal-

izer. Once again, although some non-linearities may

exist because of compression, the forward path is usu-

127

Bispo B. and Freitas D..

Evaluation of Acoustic Feedback Cancellation Methods with Multiple Feedback Paths.

DOI: 10.5220/0005068201270133

In Proceedings of the 11th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2014), pages 127-133

ISBN: 978-989-758-046-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ally assumed to be linear and deﬁned as an FIR ﬁlter

G(z,n) = g

(n) + g

(n)z

−1

+ . .. + g

−1

(n)z

−(L

−1)

= g

(n)z (2)

with length L

and has g

(n) = 0, ∀n, for closed-loop

analysis.

Let the system input signal u(n) be the source sig-

nal v(n) added to the ambient noise signal r(n), i.e.,

u(n) = v(n) + r(n), and, for simplicity, also include

the characteristics of the microphone and A/D con-

verter. The system input signal u(n) and the loud-

speaker signal x(n) are related by the system closed-

loop transfer function as

X(z) =

G(z,n)

1− G(z,n)F(z,n)

U(z). (3)

According to the Nyquist’s stability criterion, the

closed-loop system will become unstable if there is at

least one frequency ω such that

(



G(e

,n)F(e

,n)



≥ 1

∠G(e

,n)F(e

,n) = 2kπ, k ∈ Z.

(4)

It means that if at least one frequency compo-

nent is reinforced after traversing the system open-

loop transfer function G(z,n)F(z,n) and is added to

the input signal u(n) with no phase shift, this fre-

quency component will never disappear from the sys-

tem even if there is no more input signal. After each

loop through the system, its amplitude will increase

causing a howling at that frequency, a phenomenon

known as Larsen effect (Rombouts et al., 2006; van

Waterschoot and Moonen, 2011). This howling will

be very annoying for all listeners present and the sys-

tem gain generally has to be reduced. As a conse-

quence, the maximum stable gain (MSG) of the PA

system is limited by the occurrence of acoustic feed-

back (Rombouts et al., 2006; van Waterschoot and

Moonen, 2011).

In order to eliminate or, at least, to control the

Larsen effect, several methods have been developed

over the past decades (van Waterschoot and Moonen,

2011). The acoustic feedback cancellation (AFC)

methods identify and track the acoustic feedback path

F(z,n) using an adaptive ﬁlter that is generally de-

ﬁned as an FIR ﬁlter

H(z,n) = h

(n) + h

(n)z

−1

+ . .. + h

−1

(n)z

−(L

−1)

= h

(n)z (5)

with length L

. Then, the feedback signal f(n) ∗ x(n)

is estimated as h(n) ∗ x(n) and subtracted from the

microphone signal y(n) so that, ideally, only the sys-

tem input signal u(n) is processed by the forward path

G(z,n). Such a scheme is shown in Fig. 2.

Forward

Path

Adaptive Feedback

Path

Filter

P P

G(z, n)

H(z, n)

y(n) u(n) v(n)

r(n)

F (z, n)

e(n)

x(n)

Figure 2: Typical AFC system.

But, because of the presence of the forward path

G(z,n), the estimation noise (system input u(n)) and

input (loudspeaker x(n)) signals to the adaptive ﬁlter

are highly correlated. Then, if the traditional adap-

tive ﬁltering algorithms based on the Wiener theory

or least squares are used, a bias is introduced in the

estimate of the acoustic feedback path (Siqueira and

Alwan, 2000; Hellgren and Forssell, 2001). As un-

desired consequences, the adaptive ﬁlter H(z,n) will

only partially cancel the feedback signal f(n) ∗ x(n)

and will also apply distortions in the system input sig-

nal u(n).

Mostly, the solutions existing in the literature to

overcome the bias in the estimate of the feedback

path try to, somehow, decorrelate the loudspeaker

x(n) and system input u(n) signals. Among them, the

PEM-AFROW stands out for having the best perfor-

mance (Rombouts et al., 2006; van Waterschoot and

Moonen, 2011). Recently, one method that extracts

well-deﬁned information from the cepstrum of the mi-

crophone signal to update the adaptive ﬁlter was pro-

posed (Bispo et al., 2013). However, until nowadays,

only results in PA systems with a single feedback path

were presented.

The present work evaluates the performance of

some state-of-art AFC methods in a more realistic

scenario with multiple feedback paths. The paper

is organized as follows: Section 2 presents a typical

PA system with multiple feedback paths; Section 3

brieﬂy presents the AFC methods under evaluation;

Section 4 describes the conﬁguration of the simulated

experiments; in Section 5, the obtained results are pre-

sented and discussed. Finally, Section 6 concludes the

paper emphasizing its main contributions.

2 AFC SYSTEM WITH

MULTIPLE FEEDBACK PATHS

Typically, aiming to be heard by a large audience in

the same acoustic environment, a speaker uses a PA

system with one microphone, responsible for picking

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

128

up his/her own voice, one ampliﬁcation system, re-

sponsible for amplifying the voice signal, and several

loudspeakers placed in different positions, responsi-

ble for playback and distributing the voice signal in

the acoustic environment so that everyone in the au-

dience can hear it.

Such typical PA system with 1 microphone and

C loudspeakers is showed in Fig.3. The loudspeaker

signal x(n), after played back by the kth-loudspeaker,

may be picked up by the microphone going through

the feedback path F

(z,n). The C acoustic feedback

signals f

(n) ∗ x(n) are added to the system input sig-

nal u(n), generating the microphone signal

y(n) = u(n) +

∑

k=1

(n) ∗ x(n). (6)

Then, the feedback signals are estimated as h(n)∗

x(n) and subtracted from the microphone signal y(n),

generating the error signal

e(n) = u(n) +

∑

k=1

(n) ∗ x(n) − h(n) ∗ x(n)

= u(n) +

∑

k=1

(n) − h(n)

∗ x(n),

(7)

which is effectively the signal to be processed by the

forward path G(z,n). The error signal e(n) will con-

tain no acoustic feedback as desired if

H(z,n) =

∑

k=1

(z,n). (8)

In this multiple feedback paths scenario, the adap-

tive ﬁlter has an optimum solution equal to the sum of

the single acoustic feedback paths. Indeed, the AFC

system with multiple feedback paths in Fig.3 can be

simpliﬁed to the AFC system with single feedback

path in Fig. 2 by considering F(z,n) as the overall

acoustic feedback path such that

F(z,n) =

∑

k=1

(z,n). (9)

However, in this case, F(z,n) generally has more

prominent peaks and a lower sparseness which have

inﬂuence on the performance of adaptive ﬁltering al-

gorithms (Das and Chakraborty,2012). Therefore, the

evaluation of AFC methods using multiple feedback

paths is essential because it corresponds to a more re-

alistic scenario of a typical PA system.

3 EVALUATED AFC METHODS

In this Section, a brief description of the AFC meth-

ods under evaluation is presented.

Feedback

Path

Feedback

Path

Forward

Path

Adaptive

Filter

P P

y(n)e(n)

(z, n) F

(z, n)G(z, n)

H(z, n)

x(n)

u(n)

Figure 3: Typical AFC system with multiple feedback

paths.

3.1 AFC Based on Whitening

Pre-ﬁltering

The PEM-AFROW method considers that the system

input signal u(n) can be approximated according to

U(z) = M(z,n)W(z), (10)

where w(n) is a white noise with zero mean and the

inverse source model M

−1

(z,n) is deﬁned as

−1

(z,n) = A(z,n)B(z,n), (11)

where A(z,n) is a short-time prediction ﬁlter that

models the vocal tract and B(z,n) is a long-time pre-

diction ﬁlter that models the periodicity.

From each frame of the error signal e(n) which

is expected to be close to u(n), the PEM-AFROW

method estimates A(z, n) using the well-known

Levinson-Durbin algorithm and thereafter B(z,n) us-

ing a one-tap ﬁlter with lag equal to the pitch pe-

riod. Then, the method pre-ﬁlters the loudspeaker

x(n) and microphone y(n) signals with the inverse

source model in order to obtain whitened versions of

them. Finally, these whitened signals are used to up-

date the adaptive ﬁlter according to the NLMS algo-

rithm (Rombouts et al., 2006).

3.2 AFC Based on Cepstrum of the

Microphone Signal

In an AFC system as depicted in

Fig. 2, if



G(e

jω

,n)H(e

jω

,n)



< 1 and



G(e

jω

,n)



F(e

jω

,n) − H(e

jω

,n)





< 1, the cep-

strum of the microphone signal y(n) is deﬁned

as (Bispo et al., 2013)

(τ) =c

(τ) +

∞

∑

k=1

∗k

(n)

∗

[f(n) − h(n)]

∗k

+ (−1)

k+1

∗k

(n)

(12)

where {·}

∗k

denotes the kth convolution power.

EvaluationofAcousticFeedbackCancellation-MethodswithMultipleFeedbackPaths

129

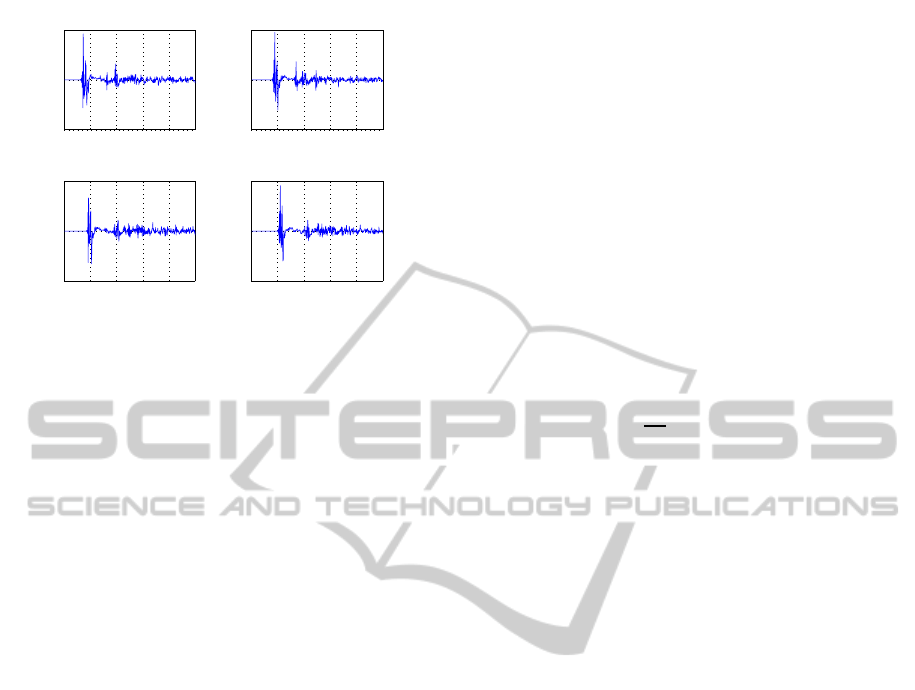
0 100 200 300 400 500

−0.2

0.2

Samples

Amplitude

0 100 200 300 400 500

−0.2

0.2

Samples

Amplitude

0 100 200 300 400 500

−0.2

0.2

Samples

Amplitude

0 100 200 300 400 500

−0.2

0.2

Samples

Amplitude

Figure 4: Impulse responses of the acoustic feedback paths

(zoom in the ﬁrst 500 samples).

From (12), the AFC-CM method extracts {g(n) ∗

f(n)}b, an instantaneous estimate of the system open-

loop impulse response, and thereafter obtains

f(n), an

instantaneous estimate of the impulse response of the

feedback path. Finally, the method updates the adap-

tive ﬁlter according to (Bispo et al., 2013)

h(n) = λh(n− 1) + (1− λ)

f(n), (13)

where 0 ≤ λ < 1 is the factor that controls the trade-

off between robustness and tracking rate of the adap-

tive ﬁlter.

4 SIMULATION

CONFIGURATIONS

To assess the performance of the AFC methods, an

experiment was made in a simulated environment to

measure its abilities to increase the maximum stable

gain of a PA system. For this purpose, the following

conﬁguration was used.

4.1 Simulated Environment

In order to simulate a PA environment with multi-

ple feedback paths, 4 measured impulse responses of

the same room, from (Jeub et al., 2009), were used

as the impulse response f

of the acoustic feedback

paths. The impulse responses was downsampled to

= 16 kHz and then truncated to length L

= 4000

samples, and are illustrated in Fig. 4.

The forward path, that is the ampliﬁer of the PA

system, was simply deﬁned as an unity delay and a

gain according to

G(z,n) = g

(n)z

−1

, (14)

with length L

= 2.

The insertion of a delay ﬁlter immediately after

the forward path G(z,n) is a common practice in the

AFC methods. Then, the forward path G(z,n) was

followed by a delay ﬁlter

D(z) = z

−(L

−1)

(15)

with length L

= 401 so that generates a time delay

of 25 ms.

4.2 Maximum Stable Gain

In order to measure the maximum stable gain of

the PA system, a broadband gain K(n) was deﬁned,

similarly to (van Waterschoot and Moonen, 2011),

as the average magnitude of the frequency response

G(e

jω

,n) of the forward path

K(n) =

2π

∑

ω=0

|G(e

jω

,n)|, (16)

and is extracted from G(z,n) by

G(z,n) = K(n)J(z,n). (17)

Considering that J(z,n) is known, the maximum

stable gain (MSG) was deﬁned as

MSG(n)(dB) = 20log

K(n)

such that max

ω∈P(n)



G(e

jω

,n)D(e

jω

)F(e

jω

,n)



= 1,

(18)

resulting in (19), where P(n) denotes the set of fre-

quencies that fulﬁll the phase condition in (4), also

called critical frequencies of the PA system, and is

deﬁned as (20).

The MSG of the PA system with no AFC method

was deﬁned as MSG

= 20log

. K(n) was initial-

ized to a value K

such that 20log

< MSG

order to allow the AFC method to operate in a stable

condition and thus the adaptive ﬁlter to converge. As

suggested in (van Waterschoot and Moonen, 2011), it

was deﬁned that 20log

= MSG

− 3, i.e., a 3 dB

initial gain margin.

In a ﬁrst conﬁguration, K(n) remained at the same

value, K(n) = K

, during all the simulation time

T = 20 s in order to verify the methods’ performance

for a time-invariant forward path G(z, n). In a more

practical conﬁguration, K(n) = K

until 5 s and then

20log

K(n) was increased at the rate of

1dB

/s up to

20log

such that 20log

= 20log

+ ∆K.

Finally, K(n) = K

during 10 s totaling a simulation

time T = 15+ ∆K s.

As the main goal of the AFC methods is to in-

crease the MSG of the PA system, it is necessary to in-

clude the frequencyresponse H(e

jω

,n) of the adaptive

ﬁlter in the MSG measurement. Then, the MSG of a

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

130

MSG(n)(dB) = −20log



max

ω∈P(n)



J(e

jω

,n)D(e

jω

)F(e

jω

,n)





. (19)

P(n) =



ω|∠G(e

jω

,n)D(e

jω

)F(e

jω

,n)= 2kπ,k ∈ Z



. (20)

MSG(n)(dB) = −20log



max

ω∈P

(n)



J(e

jω

,n)D(e

jω

)



F(e

jω

,n) − H(e

jω

,n)







. (21)

∆MSG(n)(dB) = −20log

max

ω∈P

(n)



J(e

jω

,n)D(e

jω

)



F(e

jω

,n) − H(e

jω

,n)





max

ω∈P(n)

|J(e

jω

,n)D(e

jω

)F(e

jω

,n)|

. (22)

(n) =



ω|∠G(e

jω

,n)D(e

jω

)



F(e

jω

,n) − H(e

jω

,n)



= 2kπ, k ∈ Z



. (23)

PA system with an AFC method was deﬁned as (21).

Moreover, the increase in MSG provided by the AFC

method, ∆MSG, was deﬁned as (22). In both equa-

tions, P

denotes the set of frequencies that fulﬁll the

phase condition of the system with the insertion of

the adaptive ﬁlter, also called critical frequencies of

the AFC system, as deﬁned according to (23).

4.3 Frequency-weighted Log-spectral

Signal Distortion

The sound quality was measured by the frequency-

weighted log-spectral signal distortion deﬁned as (van

Waterschoot and Moonen, 2011)

SD(n) =

∑

ω=ω

w(ω)



10log

jω

,n)

jω

,n)



, (24)

where S

jω

,n) and S

jω

,n) are the short-term

power spectrum density of the error signal e(n) and

system input signal u(n), respectively, and w(ω)

is a weighting function that gives equal weight to

each auditory critical band between ω

= 0.0375π

(equivalent to 300 Hz) and ω

= 0.8π (equivalent to

6400 Hz) (ANSI, 1997). The short-term power spec-

trum densities S

jω

,n) and S

jω

,n) are computed

using frames of 20 ms.

Indeed, SD(n) quantiﬁes the distortion inserted in

the error signal e(n) in comparison with the system

input signal u(n). The SD(n) value will be as low

as the inserted distortion is and has optimum value

SD(n) = 0 when e(n) = u(n). In general, SD(n) → 0

as long as e(n) → u(n).

4.4 Speech database

The signals database used in the simulations was

formed by 10 speech signals. Each speech signal

was composed of several basic signals from a speech

database. Each basic signal consisted of one 4 s short

sentence with original sampling rate of 48 kHz but

downsampled to f

= 16 kHz. All basic signals were

recorded in the talkers native language, and their na-

tionalities and genders were the following:

• 4 Americans (2 males and 2 females)

• 2 British (1 male and 1 female)

• 2 French (1 male and 1 female)

• 2 Germans (1 male and 1 female)

But since the performance assessment of adap-

tive ﬁlters needs longer signals, several basic sig-

nals from the same talker were concatenated and had

their silence parts removed by a voice activity detec-

tor (VAD), resulting in the mentioned 10 speech sig-

nals (1 signal per talker).

5 SIMULATION RESULTS

This Section compares the performance of the AFC

methods under evaluation using speech signal as the

source signal v(n). The evaluation was done in a situ-

ation close to real-world conditions where the source-

signal-to-noise ratio (SNR) was 30 dB. With the ex-

ception of the adaptive ﬁlters’ parameters, the param-

eters of all methods had the same values as originally

proposed(adjusted to f

= 16 kHz in the case of PEM-

AFROW).

The optimization of the adaptive ﬁlter parameters

(λ and L

in the case of the AFC-CM, and stepsize

µ, normalization parameter δ and L

of the PEM-

AFROW) was performed for each signal. From a pre-

deﬁned range for each one, the values were chosen

empirically in order to optimize the curve MSG(n),

and consequently ∆MSG(n), in terms of minimum

area of instability and, secondarily, of maximum

mean value within the simulation time. The optimal

curves for the kth signal were deﬁned as MSG

(n)

and ∆MSG

(n) while the respective SD(n) curve as

(n).

EvaluationofAcousticFeedbackCancellation-MethodswithMultipleFeedbackPaths

131

Then, the optimal average curves MSG

(n),

∆MSG

(n) and SD

(n) were obtained by averaging

the optimal curves of each signal according to

MSG

(n) =

∑

k=1

MSG

(n), (25)

∆MSG

(n) =

∑

k=1

∆MSG

(n), (26)

and

(n) =

∑

k=1

(n). (27)

And their respective mean values were deﬁned as

MSG

∑

n=1

MSG

(n), (28)

∆MSG

∑

n=1

∆MSG

(n), (29)

and

∑

n=1

(n), (30)

where N

is the number of samples relating to the

simulation time. In addition, the asymptotic value of

∆MSG

was deﬁned as

−−−−→

∆MSG

, which represents the

MSG increase provided by the AFC methods, and was

estimated only by inspection of the curve.

In the ﬁrst conﬁguration, the broadband gain K(n)

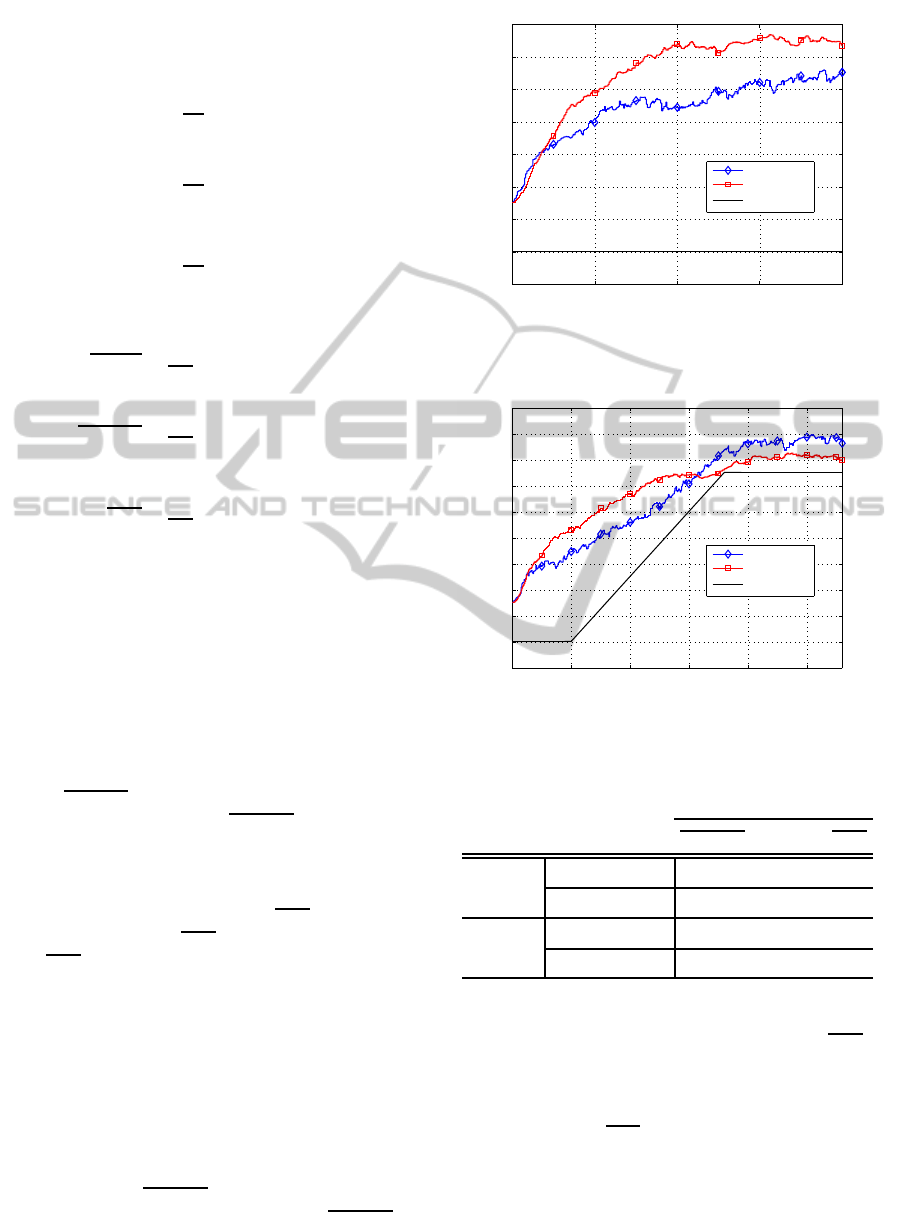
remained constant, i.e., ∆K = 0. Fig. 5 shows the re-

sults obtained by the AFC methods under evaluation

for ∆K = 0. As can be observed, the AFC-CM method

outperformed the PEM-AFROW. The PEM-AFROW

obtained

∆MSG

= 5.6 dB and

−−−−→

∆MSG

≈ 7.4 dB

while the AFC-CM achieved

∆MSG

= 7.9 dB and

−−−−→

∆MSG

≈ 10 dB.

With respect to sound quality, the same order of

performance was obtained but with very similar re-

sults. The PEM-AFROW obtained

= 1.9 while

the AFC-CM achieved SD

= 1.8. These low and

similar

values may be explained by the fact that,

with such ﬁxed value of K(n) and with the increase in

MSG provided by all the AFC methods, the systems

were too far from the instability.

In the second conﬁguration, K(n) was increased

by ∆K = 13 dB. Fig. 6 shows the results obtained

by the AFC methods for ∆K = 13 dB. As can

be observed, the AFC-CM outperformed the PEM-

AFROW in the ﬁrst half of the simulation runtime

while the opposite occurs in the second half. The

AFC-CM obtained

∆MSG

= 8.5 dB and

−−−−→

∆MSG

≈

11.2 dB while the PEM-AFROW achieved

∆MSG

8.2 dB and

−−−−→

∆MSG

≈ 12.4 dB.

0 5 10 15 20

−14

−12

−10

−8

−6

−4

−2

Time (s)

MSG

(n) (dB)

PEM−AFROW

AFC−CM

20log

K(n)

Figure 5: Average results of the methods for speech signal

and ∆K = 0.

0 5 10 15 20 25

−14

−12

−10

−8

−6

−4

−2

Time (s)

MSG

(n) (dB)

PEM−AFROW

AFC−CM

20log

K(n)

Figure 6: Average results of the methods for speech signal

and ∆K = 13.

Table 1: Summary of results obtained by the PEM-AFROW

and AFC-CM methods using speech as source signal.

∆MSG

−−−−→

∆MSG

∆K = 0

PEM-AFROW 5.6 7.4 1.9

AFC-CM 7.9 10 1.8

∆K = 13

PEM-AFROW 8.2 12.4 3.1

AFC-CM 8.5 11.2 3.7

In terms of sound quality, the AFC-CM method

presented the worst performance by achieving SD

3.7 because it had a low stability margin after t = 17 s,

as can be observed in Fig. 6, which resulted in an ex-

cess reverberation in the error signal e(n). The PEM-

AFROW obtained

= 3.1.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

132

6 CONCLUSIONS

Acoustic feedback limits the maximum stable gain of

a public address system and thus may cause the sys-

tem to become unstable resulting in a howling at a

speciﬁc frequency, a phenomenon known as Larsen

effect. Acoustic feedback cancellation methods use

an adaptive ﬁlter to identify the impulse response of

the acoustic feedback path and then remove its in-

ﬂuence from the system. However, since in such a

system the source and loudspeaker signals are corre-

lated, acoustic feedback cancellation methods that use

traditional adaptive ﬁltering algorithms based on the

Wiener theory or least squares present a bias in the

estimate of the acoustic feedback path if no decorre-

lation algorithm is used.

Several methods have been proposed to overcome

the bias problem. However, the methods are generally

evaluated considering a public address system with

only one microphone and one loudspeaker. This work

evaluates some of the state-of-art methods consider-

ing a public address system with one microphone and

four loudspeakers that results in multiple feedback

paths and corresponds to a more realistic scenario of

a typical system.

Simulation results demonstrated that, with multi-

ple feedback paths, the AFC methods are able to in-

crease in around 12 dB the maximum stable gain of

the public address system when the source signal is

speech.

ACKNOWLEDGEMENTS

This work was partially supported by FCT

- Fundac¸˜ao para a Ciˆencia e a Tecnologia

(SFRH/BD/49038/2008) and by the project

AAL4ALL - FCOMP-01-0124-FEDER-13852,

co-ﬁnanced by European Community Fund FEDER

through COMPETE - Programa Operacional Factores

de Competitividade (POFC).

REFERENCES

ANSI (1997). ANSI S3.5: American national standard

methods for calculation of the speech intelligibility in-

dex. American National Standard Institute.

Bispo, B. C., Rodrigues, P. M. L., and da S. Freitas, D. R.

(2013). Acoustic feedback cancellation based on cep-

stral analysis. In Proceedings of 17th IEEE Confer-

ence on Signal Processing Algorithms, Architectures,

Arrangements and Applications, pages 205–209, Poz-

nan, Poland.

Das, R. L. and Chakraborty, M. (2012). Sparse adaptive ﬁl-

ters - an overview and some new results. In Proceed-

ings of the 2012 IEEE International Symposium on

Circuits and Systems, pages 2745–2748, Seoul, Soutjh

Korea.

Hellgren, J. and Forssell, U. (2001). Bias of feedback

cancellation algorithms in hearing aids based on di-

rect closed loop identiﬁcation. IEEE Transactions on

Speech and Audio Processing, 9(7):906–913.

Jeub, M., Sch¨afer, M., and Vary, P. (2009). A binaural room

impulse response database for the evaluation of dere-

verberation algorithms. In Proc. International Confer-

ence on Digital Signal Processing, Santorini, Greece.

Rombouts, G., van Waterschoot, T., Struyve, K., and

Moonen, M. (2006). Acoustic feedback cancellation

for long acoustic paths using a nonstationary source

model. IEEE Transactions on Signal Processing,

54(9):3426–3434.

Siqueira, M. G. and Alwan, A. (2000). Steady-state analysis

of continuous adaptation in acoustic feedback reduc-

tion systems for hearing-aids. IEEE Transactions on

Speech and Audio Processing, 8(4):443–453.

van Waterschoot, T. and Moonen, M. (2011). Fifty years of

acoustic feedback control: state of the art and future

challenges. Proceedings of the IEEE, 99(2):288–327.

EvaluationofAcousticFeedbackCancellation-MethodswithMultipleFeedbackPaths

133