Automatic Segmentation of MR Brain Tumor Images using Support

Vector Machine in Combination with Graph Cut

Elisabetta Binaghi

, Massimo Omodei

, Valentina Pedoia

Sergio Balbi

, Desiree Lattanzi

and Emanuele Monti

Department of Theoretical and Applied Science, Insubria University, Varese, Italy

Department of Biotechnologies and Life Sciences, Insubria University, Varese, Italy

Keywords: MRI Segmentation, Brain Tumor Segmentation, Meningioma, Graph Cut, Support Vector Machine.

Abstract: This work focuses the attention on the automatic segmentation of meningioma from multispectral brain

Magnetic Resonance imagery. The Authors address the segmentation task by proposing a fully automatic

method hierarchically structured in two phases. The preliminary unsupervised phase is based on Graph Cut

framework. In the second phase, preliminary segmentation results are refined using a supervised

classification based on Support Vector Machine. The overall segmentation procedure is conceived fully

automatic and tailored to non-volumetric data characterized by poor inter-slice spacing, in an attempt to

facilitate the insertion in clinical practice. The results obtained in this preliminary study are encouraging and

prove that the segmentation benefits from the allied use of Graph Cut and Support Vector Machine

frameworks.

1 INTRODUCTION

Magnetic Resonance (MR) imaging has become an

important tool for the clinical study of brain

pathologies. The high resolution and contrast and

good soft tissue differentiation allow physicians

accurately locate specific pathologies. A precise

segmentation of pathological and healthy tissues

composing the MR image is important for

understanding the pathology, for evaluating the

evolutionary trend, for planning the best surgical

approach or possible alternative solutions.

Automated methods of segmentation represent a

valuable solution by supporting human operators

with varying degrees of automation, in tracing the

boundaries of the different tissue regions and by

automatically providing volumetric computation of

the pathological MRI signal (Clark et al., 1995, Kaus

et al., 2001; Withey and Koles, 2008; Balafar et al.,

2010).

The last 20 years have seen a rapid growth in the

use of semi-automatic or fully automatic

segmentation methods in MR brain tumor studies.

Several techniques have been proposed in studies

distinguished by the type of brain tumor treated, by

the tissue features extracted in different MRI

modalities. The proposed techniques make use of

individual images or multispectral patterns and are

supervised or unsupervised (Gordillo et al. 2013,

Bauer et al. 2013). Despite the sizable achievement

obtained, novel approaches are continuously

investigated to provide robust solutions and fulfil

hard accuracy and reproducibility requirements. In

the last few years Support Vector Machine (SVM)

methods (Vapnik 1995; Schoelkopf and Smola

2002) have shown excellent performances in MRI

segmentation studies aimed at identifying a variety

of neurological conditions (Verma et al. 2008, Bauer

et al., 2013). Recent studies propose the allied use

of SVM and regularisation procedures to introduce

spatial consistency in classification results (Bauer et

al. 2011).

This work focuses the attention on the automatic

segmentation of meningioma from multi-spectral

brain MR imagery. Meningioma is one of the few

benign tumors found in the brain region. Precise

tumor detection contributes to formulate surgical

indications in elderly patients harboring intracranial

meningiomas and supports surgical planning for a

complete surgical resection (Greenberg et al. 1999,

Caroli et al. 2005).

The Authors address the segmentation task by

proposing a fully automatic method hierarchically

structured in two phases. The preliminary

unsupervised phase is based on Graph Cut

152

Binaghi E., Omodei M., Pedoia V., Balbi S., Lattanzi D. and Monti E..

Automatic Segmentation of MR Brain Tumor Images using Support Vector Machine in Combination with Graph Cut.

DOI: 10.5220/0005068501520157

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 152-157

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

framework (Boykov and Funka-Lea 2006). In the

second phase preliminary segmentation results are

refined using a supervised classification based on

Support Vector Machine (SVM) (Vapnik 1995). The

supervised classification makes use of multichannel

intensities of Post Gadolinium T1-weighted (T1c)

and T2-weighted FLAIR image (T2f). Additional

textural and contextual features are considered and

systematically added during the experimentation in

order to measure their effective contribution. The

proposed hybrid strategy synergically combines the

mutual advantages of the unsupervised and

supervised techniques. The Graph Cut segmentation

takes into account topological constraints and

identify spatially consistent regions subsequently

refined by the SVM which is able to capture

complex multivariate relationships in the data.

The overall segmentation procedure is conceived

fully automatic and tailored to non-volumetric data

characterized by poor inter-slice spacing, in an

attempt to facilitate the insertion in current clinical

practice.

2 THEORETICAL

BACKGROUND

This section briefly outlines the basic concepts of

Graph Cut and SVM adopted in the proposed hybrid

segmentation strategy.

2.1 Graph Cut

Within the graph theoretical approach, the

segmentation problem is modeled in terms of

partitioning a graph into several sub-graphs such that

each of them represents a meaningful object of

interest in the image (Wu and Leahy, 1993; Rother

et al. 2004, Peng and Liu, 2010). Proceeding from

these principles several methods were investigated.

The aim of a volumetric segmentation

problem is to assign to each voxel v ∈ V a label

representing the membership of the voxel to a

specific region Li; in the case of binary

segmentation aimed to subdivide the image into

Object (Obj) and Background (Bkg), the goal is to

find the optimal labeling L = (L

Bkg

Obj

). We

assume that each voxel v has two cost values,

Rv(O

Obj

) and Rv(O

Bkg

), related to Object and

Background labeling respectively. Each pair of

voxels (v,w) belonging to the set N of pairs of 3D

neighboring voxels has a cost B

v;w

. The cost B

v;w

related to the type of labeling of the pair of voxels.

The optimal labeling L = (L

Bkg

Obj

) is obtained by

minimizing the following cost function:





LBLRLE 

where











ORLR











Nwv

Lwv

BLB

;













if 1

if 0

R(L) and B(L) are called Regional and Boundary

terms respectively. The application of Graph Cut

requires the identification of object and background

prototypes with which to initialize the overall

segmentation process. Usually this task is

accomplished through an interactive session in

which users manually select seeds on the image.

Recently there have been some proposals

exploiting solutions for automatically initializing

Graph Cut-based segmentations of biomedical

images (Santle et al., 2012).

The present study uses the max-flow/min-cut

algorithm (Boykov and Kolmogorov 2004) as

optimization framework and adopts an automated

initialization procedure based on k-means clustering

algorithm.

2.2 SVM

SVM is a classification algorithm based on kernel

methods (Vapnik 1995; Schoelkopf and Smola

2002) able to map the original parameter vectors

into a higher (possibly infinite) dimensional feature

space through a kernel function. Classes which are

non-linearly separable in the original space can be

linearly separated in the higher dimensional feature

space.

Let {(xi, yi)} a supervised training set of

elements for a two-class classification problem,

with xi  X  Rn and yi  {-1, 1}. Considering

the case of linearly separable data, the solution to

the classification problem consists in the

construction of the decision function

w, b

(x) = sgn(g

w, b

(x)) with g

w, b

(x) = w

x+ b

that can correctly classify an input pattern x that is

not necessarily from the training set.

SVM classifier defines the hyperplane that

causes the largest separation between the decision

function values for the “borderline” examples from

the two classes. Mathematically, this hyperplane can

be found by minimizing the cost function:

AutomaticSegmentationofMRBrainTumorImagesusingSupportVectorMachineinCombinationwithGraphCut

153

)( WWJ 

subject to

1for y 1





bXW

The extension to the nonlinear classification is

based on the function g’= W

φ (X ) + b in which

the non liner operator φ (.) is introduced.

In this case the SVM cost function to be

minimized is

),(







CWWJ

subject to







1,2,....li ,0 with1



bXwy

Linearly non separable data are analyzed with kernel

functions such as higher order polynomials and

Gaussian Radial Basis Functions (RBF). Suykens

(Suykens et al. 2002) proposed a new formulation of

SVM by adding a least squares (LS) term in the

original formulation of the cost function.

3 FULLY AUTOMATED

MENINGIOMA

SEGMENTATION

The salient aspect of the overall segmentation

strategy is the use of a supervised learning procedure

based on SVM model, able to learn from a set of

labeled image elements the invariant common

properties of the pathological and healthy classes.

The trained classifier automatically assigns labels to

elements never seen during the training phase.

The use of the two MR modalities, T1c and T2f,

is motivated by the fact that each scan depicts

different characteristics of the tissues. The combined

use of the two images allows obtaining higher

discriminant power than just by analyzing one of

them.

The SVM classifier acts as a dichotomizer

receiving in input a multidimensional pattern

including intensities of T1c and T2f MR elements

and contextual/textural features derived from the

two scans respectively. The supervised classification

procedure is built on the top of an unsupervised

unidimensional Graph Cut-based segmentation of

T1c and T2f MR images. The unsupervised stage

facilitates the subsequent supervised task by

identifying an intermediate hybrid class distributed

in a limited area and subsequently subdivided by the

SVM in meningioma and healthy tissue.

Before the segmentation process, T1c and T2f

MR images are co-registered for their combined use

in the analysis and a logarithmic contrast

enhancement is applied in order to enhance the

similarity between the edema and brain tissues in the

T2f image.

3.1 Graph Cut Based Segmentation

Graph Cut segmentation is separately applied to T1c

and T2f images allowing the labeling of intermediate

hybrid regions. The intersection of these initially

identified regions is subsequently analyzed and

classified by the SVM to identify meningioma areas.

The initialization of the Graph Cut segmentation is

automatically accomplished through the use of the k-

means clustering algorithm. The segmentation of

T1c image in three sub-volumes allows to identify a

hybrid region including all the contrast enhanced

tissues: meningioma, vessel and skull tissues.

From the segmentation of T2f image a partition

of the original volume in three regions is also

obtained corresponding to “air”,

“brain/edema/meningioma” and “skull” respectively.

By intersecting the hybrid region originally

identified in T1c with the

“brain/edema/meningioma” region identified in T2f

we obtain a refined region of interest to be presented

in input to the SVM classifier for the identification

of meningioma areas.

3.2 Supervised Multispectral

Classification

The present study considers the following features:

gray scale values from T1c and T2f scans (I

t1c

t2f

first order texture features: mean (M) , variance

(Var), skewness (S), kurtosis (K) and entropy (E)

computed on T1c and T2f scans, intensities in

neighborhoods of voxels of both scans (I1-I26) . All

proposed features have been analyzed systematically

in the experimental evaluation phase in order to

determine the combination that is most appropriate

for the classification task (see section 4). The

features have been normalized to have zero mean

and unit variance.

A binary hard categorization is performed by the

SVM classifier that labels co-registered voxels

belonging to the region identified in the

unsupervised phase, as Meningioma (M) and

Healthy tissue (H). The SVM classifier is configured

as soft-margin LS model with Kernel RBF. During

the training phase, the SVM learns an approximation

for the true input–output relationship based on a

given training set of examples constituted by N

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

154

input-output pairs



N,1,i ,, 

. The input

pattern

],..[

ffx 

is an m-dimensional feature

vector where m is the number of features considered

in the current configuration, and



HMy

,

is a

supervised label denoting the membership in the

meningioma or healthy class.

After the segmentation, if the tumor area presents

necrosis and dishomogeneity, small holes within the

tumor mass classified as healthy tissues may appear .

A morphological procedure is therefore used to

refine the segmented masks making the tumor area

segmented more solid and compact.

4 EXPERIMENTS

The segmentation method was experimented on

multispectral datasets of 10 patients. Each dataset is

composed of T1c and T2f scans. The T1c is acquired

using a 3D sequence characterized by 1 mm

isotropic voxels, the inter-slice spacing of 1 mm and

the slice thickness of 1 mm; the T2f sequence

includes an in-plane resolution between 0,75 and

0,81 mm and slice thickness of 5 mm. The spacing

between slice is 6 mm for cases 1,3,6,7,8,10 and of

6.5 mm for cases 2,4,5,9. Performances were

assessed by adopting a behavioral comparison

strategy in which the masks obtained by the

automated segmentation were compared with the

masks obtained through a manual segmentation of

the T1c images. Manual labeling was performed by

a team of three experts with the support of a slice-

by-slice manual annotator.

The strategy adopted for the definition of a

suitable reference standard starting from

combination of multiple manual segmentations, is

Majory Voting (Heckemann et. al 2006).

4.1 Metrics

MRI segmentation was performed with the purpose

of determining the volume of pathological tissues

and their spatial distribution. The metrics adopted

for the volume estimation error is the normalized

absolute difference in size between reference and

segmented data.

Spatial overlap between reference and automated

maps is measured in terms of Jaccard (J), Precision

and Recall indexes (Bouix et al. 2007).

Common agreement between experts and

automated segmentation is quantified directly by the

Williams’ index. If this index is greater than one for

a given rater, it can be concluded that current rater

agrees with the other raters at least as well as they

agree with each other (Williams 1972).

4.2 Results

A trial and error phase was conducted in which

several configurations of the segmentation procedure

were considered distinguished by different values of

main parameters involved.

A first set of parameters was varied to tune the

Graph Cut model and the LS-SVM classifier. The k-

means algorithm has been used to initialize Graph

Cut segmentation. The value of k parameter was set

equal to three. The k value has been assessed taking

into account the expected MR signal in both the

MRI sequences considered. The value of the

standard deviation (σ) for Gaussian RBF kernel was

chosen as 0.5 in the SVM classifier.

Different configurations of the classification

procedure were also evaluated varying the number

of training examples and the features considered.

The configuration that showed the most balanced

behavior after the trial and error phase is based on

the following vector of features







ftcti

EKSVarMIx

xxx

222222

111111

,,,,,

with,



and used a training set of 10.000 labeled samples

randomly chosen within the ground truth masks.

Table 1: Mean values of Jaccard, Precision, Recall and

Volume Error obtained by performing the leave-one-out

cross-validation (Interpatient) and by training and testing

the classifier on the same dataset (Intrapatient).

Jaccard

Index

Precision Recall

Volume

Error

(%)

Interpatient

Mean 0.867 0.814 0.942 16.087

Std 0.072 0.095 0.081 11.145

Intrapatient

Mean 0.959 0.967 0.991 4.750

Std 0.031 0.031 0.004 3.152

As shown in Table 1, for the intrapatient

analysis, the mean Jaccard coefficient over all 10

patients is 0.959, Precision and Recall have a value

equal to 0,967 and 0,991 respectively; the Volume

Estimation Error is equal to 4,750. The interpatient

analysis has provided a Jaccard cofficient equal to

0,867, Precision and Recall equal to 0,814 and

0,942 respectively and a Volume Estimation Error

equal to 16,087.

In Table 2 the results obtained using the

Williams’ index are listed. Numerical values clearly

AutomaticSegmentationofMRBrainTumorImagesusingSupportVectorMachineinCombinationwithGraphCut

155

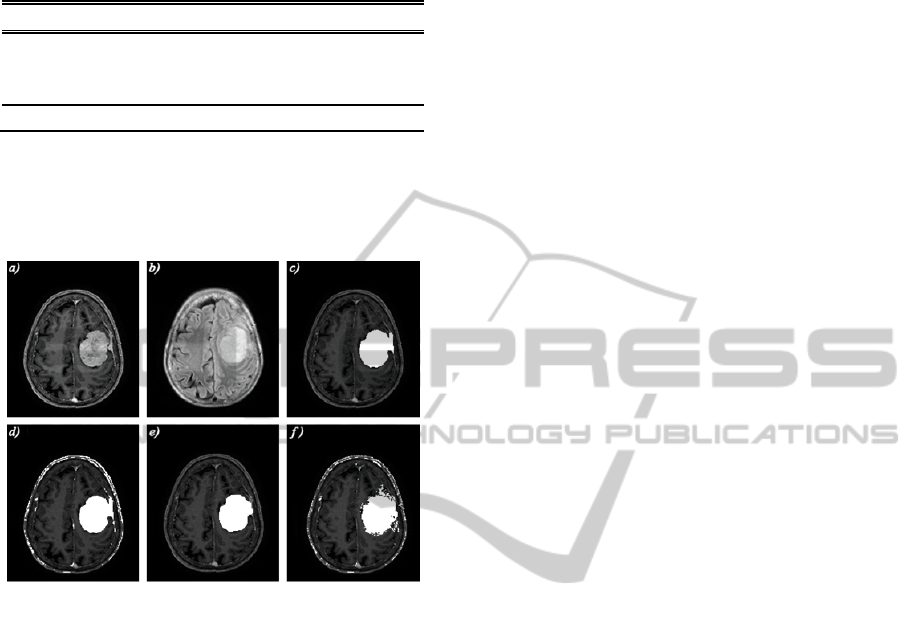
Table 2: Williams’ Indexes obtained by considering the

manual segmentations (E1-E3) and the automatic

segmentation (A) of the 10 cases under study.

W. I. 1 2 3 4 5 6 7 8 9 10

E1 1.0 1.0 1.0 1.0 1.0 0.9 0.9 1.0 0.9 1.0

E2 0.9 0.9 1.0 0.9 0.9 1.0 1.0 1.1 0.9 0.9

E3 0.9 1.0 0.9 1.0 0.9 1.0 1.0 0.7 1.0 1.0

A 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.1 1.0 1.0

indicate that the automatic segmentation method has

a good behavior with respect to the inter-expert

variability and often it shows a better behavior than

other raters.

Figure 1: Results of one axial slice obtained by the

interpatient analysis. a) Original T1c image, b) Original

T2f image, c) Overlap between original T1c image and the

ground truth mask, d) Overlap between original T1c image

and the intermediate mask obtained by Graph Cut

segmentation, e-f) Overlap between original T1c image

and the final segmentation mask obtained by interpatient

analysis, considering and without considering Graph Cut

stage respectively.

Figure 1 shows an axial slice of one patient and

the results obtained considering and without

considering Graph Cut stage in the overall strategy.

Results are clearly worse when not using the Graph

Cut preliminarily. For the dataset shown in Figure 1,

we obtained a Jaccard coefficient equal to 0.21109

and Volume Error equal to 363.4476 when no Graph

Cut is applied. With the complete procedure, Jaccard

is equal to 0.856 and Volume Error is equal to 7.119.

The mean computation time for the training task is

60 seconds and for the segmentation task performed

by the trained classifier is 159 seconds (without

Graph Cut, 732 s.) on a single CPU running at 2.26

Ghz.

5 CONCLUSIONS

Our objective in this study was to develop a fully

automatic hybrid image segmentation strategy for

meningioma segmentation in Magnetic Resonance

brain images. The supervised segmentation

framework is built on the top of the Graph Cut

algorithm initialized automatically. The strategy was

tested on a preliminary collected data set. The

results prove that the allied use of Support Vector

Machine and Graph Cut produces accurate

segmentation of tumors present in scenarios of

varied complexity. Accuracy results obtained are

encouraging. Future plans contemplate the

acquisition of new data with which to perform a

more significant interpatient analysis and to develop

of a comparative evaluation with other methods.

REFERENCES

Balafar, M., Ramli, A., Saripan, M., Mashohor, S., 2010.

‘Review of brain MRI image segmentation

methods.’Artificial Intelligence Review, 33, 261–274.

Bauer, S., Nolte, L-P., Reyes, M., 2011. Fully automatic

segmentation of brain tumor images using support

vector machine classification in combination with

hierarchical conditional random field regularization.

In: MICCAI Int. Conf. on Medical Image Computing

and Computer Assisted Interventions Berlin:

Springer).

Bauer, S., Wiest, R., Nolte, L-P., Reyes, M., 2013. ‘A

survey of MRI-based medical image analysis for brain

tumor studies.’ Phys. Med. Biol., 58, R97–R129.

Boykov, Y., Kolmogorov, V., 2004. ‘ An experimental

comparison of min-cut/max-flow algorithms for

energy minimization in vision.’ PAMI , 26, 1124- 37.

Boykov, Y., Funka-Lea, G., 2006. ‘ Graph cuts and

efficient n-d image segmentation.’ Int. J. Comput.

Vision, 70, 109-131.

Bouix, S., Martin-Fernandez, M., Ungar, L., Koo,

M.N.M.S., McCarley, R.W., Shenton, M.E., 2007.

‘On evaluating brain tissue classifiers without a

ground truth.’ NeuroImage, 36, 1207–24.

Caroli, M., Locatelli M., Prada F., Beretta F., Martinelli-

Boneschi F., Campanella R., Arienta C., 2005.

‘Surgery for intracranial meningiomas in the elderly: a

clinical–radiological grading system as a predictor of ‘

J Neurosurg, 102, 290–294 .

Clarke, L.P., Velthuizen, R., Camacho, M., Heine, J.,

Vaidyanathan, M., Hall, L., Thatcher, R., Silbiger, M.

S., 1995. ‘ MRI segmentation: methods and

applications.’ Magn Reson Imaging, 13(3), 343–36.

Gordillo, N., Montseny, E, Sobrevilla, P., 2013, ‘State of

the art survey on MRI brain tumor segmentation.’

Magn Reson Imaging, 31(8), 1426-38.

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

156

Greenberg, H., Chandler, W., Sandler, H., 1999. Brain

Tumors, Oxford University Press, Oxford.

Heckemann, R.A., Hajnal, J.V., Aljabar, P., Rueckert, D.,

Hammers, A., 2006. ‘Automatic anatomical brain mri

segmentation combining label propagation and

decision fusion.’ NeuroImage, 33(1), 115 – 126.

Kaus, M., Warfield, S., Nabavi, A., Black, P. M.,

Jolesz, F. A., Kikinis, R., 2001. ‘Automated

segmentation of MRI of brain tumors.’ Radiology,

218, 586–591.

Peng, Y., Liu, R., 2010. Object segmentation based on

watershed and graph cut. In: 3rd International

Congress on Image and Signal Processing (CISP).

Rother, C., Kolmogorov, V., Blake, A., 2004.

‘”grabcut”: interactive foreground extraction using

iterated graph cuts.’ ACM Trans. Graph., 23(3), 309-

314.

Santle, K. Camilus, Govindan ,V. K., 2012. ‘ A Review

on Graph Based Segmentation.’ IJIGSP, 4(5), 1-13.

Schoelkopf, B., Smola, A. 2002. Learning with kernels:

support vector machines, regularization, optimization,

and beyond, MIT Press .

Suykens, J.A.K., Van Gestel, T., De Brabanter, J., De

Moor, B., Vandewalle, J., 2002. Least Squares

Support Vector Machines. World Scientific Publishing

Co., Singapore.

Vapnik, V.N., 1995. The Nature of Statistical Learning

Theory, Springer-Verlag, New York.

Verma, R., Zacharaki, E., Ou, Y., Cai, H., Chawla, S.,

Lee, S., Melhem, E., Wolf, R., Davatzikos, C., 2008.

‘Multiparametric Tissue Characterization of Brain

Neoplasms and Their Recurrence Using Pattern

Classification of MR Images.’ Acad. Radiol., 15(8),

966-977.

Williams, G.W., 1972. ‘Comparing the joint agreement of

several raters with another rater.’ Bio-metrics, 32,

619–627.

Withey, D., Koles, Z., 2008. ‘A review of medical image

segmentation: methods and available software.’ Int. J.

Bioelectromagn, 10(3), 125 -148.

Wu, Z., Leahy, R., 1993. ‘An optimal graph theoretic

approach to data clustering: Theory and its application

to image segmentation.’ IEEE. Trans. on Pattern

Analysis and Machine Intelligence, 15 (11), 1101-13.

AutomaticSegmentationofMRBrainTumorImagesusingSupportVectorMachineinCombinationwithGraphCut

157