Arbitrary Shape Cluster Summarization

with Gaussian Mixture Model

Elnaz Bigdeli

, Mahdi Mohammadi

, Bijan Raahemi

and Stan Matwin

Computer Science Department,Ottawa University, 600 king Evdard, Ottawa, Canada

Knowlegde Discovery and Data Mining lab, Telfelr School of Managment, University of Ottawa,

55 Laurier Ave, E. Ottawa, ON, Canada

Department of Computing, Dalhousie, 6050 Univeristy Ave, Halifax, Canada

Keywords: Density-based Clustering, Cluster Summarization, Gaussian Mixture Model.

Abstract: One of the main concerns in the area of arbitrary shape clustering is how to summarize clusters. An accurate

representation of clusters with arbitrary shapes is to characterize a cluster with all its members. However,

this approach is neither practical nor efficient. In many applications such as stream data mining, preserving

all samples for a long period of time in presence of thousands of incoming samples is not practical.

Moreover, in the absence of labelled data, clusters are representative of each class, and in case of arbitrary

shape clusters, finding the closest cluster to a new incoming sample using all objects of clusters is not

accurate and efficient. In this paper, we present a new algorithm to summarize arbitrary shape clusters. Our

proposed method, called SGMM, summarizes a cluster using a set of objects as core objects, then represents

each cluster with corresponding Gaussian Mixture Model (GMM). Using GMM, the closest cluster to the

new test sample is identified with low computational cost. We compared the proposed method with

ABACUS, a well-known algorithm, in terms of time, space and accuracy for both categorization and

summarization purposes. The experimental results confirm that the proposed method outperforms ABACUS

on various datasets including syntactic and real datasets.

1 INTRODUCTION

Nowadays, a large volume of data is being generated

which is even difficult to be captured and labelled. A

large volume of data is mainly generated in stream

and real time applications, in which, data is

generated rapidly, and cannot be stored bit by bit. As

a result, analysing and labelling such kind of data is

a main challenge (Guha et al., 2003)(Bifet et al.,

2009) (Charu et al., 2003). Lack of labelled data

draws attention to the application of clustering to

produce labelled data. The choice of clustering

algorithm strongly depends on data characteristic. In

small and noise free environment classical clustering

method like k-mean and k-median are commonly

used. However, in most of applications, there is no

knowledge about the number of clusters while the

shapes of clusters are non-convex and arbitrary. In

this case, density-based and grid-based clustering

methods are used. Using a clustering method that

generates arbitrary shape clusters is theoretically

ideal but the representation and analysis of each

cluster still causes many problems. For full

representation of arbitrary shape clusters, all the

samples of clusters should be preserved which is

impractical in many applications. In case of using

clustering in online applications, each cluster can be

representative of a specific pattern. These patterns

need to be kept for a long time and keeping the full

representation of the complex patterns tend to be

impractical. In this case, summarization and

extracting the key features of clusters are necessary.

Another application of clustering is categorizing the

unlabelled data. In this case, a set of clusters is

created and each cluster receives a label according to

its own samples. Each new sample is compared to

the clusters and the closest one is chosen as a cluster

that the new sample belongs to. In case of k-means,

the distance of a new sample to the centre of the

cluster is calculated, then, if the distance is less than

the radius of a cluster, new sample is attached to that

cluster. K-means and partition-based clustering

methods are sensitive to noise and cannot detect

clusters with arbitrary shape. This approach has been

Bigdeli E., Mohammadi M., Raahemi B. and Matwin S..

Arbitrary Shape Cluster Summarization with Gaussian Mixture Model.

DOI: 10.5220/0005071500430052

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2014), pages 43-52

ISBN: 978-989-758-048-2

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

studied in different applications but most of the

attention was towards non-arbitrary shape clustering

like k-means (Mohammadi et al., 2014)(Gaddam et

al., 2007). Arbitrary shape clustering methods

preserve all samples for each cluster and to find the

closet cluster to the new sample, distance of new

samples to all cluster members is calculated. It is

obvious that using such an approach is time

consuming. The other way to find the closet cluster

is to create a boundary for each cluster. If the new

sample is inside the boundary of a cluster then the

new sample belongs to that cluster. Finding the

boundary of arbitrary shape clusters, especially in

high dimensional problems, is a complex and time

consuming process. Moreover, it is necessary to save

too many faces to just keep borders of cluster

created by convex in higher dimension, which grows

exponentially with dimension (Kersting et al.,

2010)(Hershberger, 2009).

In this paper, we propose a new approach that fulfils

the mentioned requirements. We propose a

summarization approach to summarize arbitrary

shape clusters using Gaussian Mixture Model

(GMM). In our approach, we first find the core

objects of clusters and then we consider these core

objects as centres of GMM and represent a cluster

with a GMM. Since, GMM-based method keep all

statistical information of each cluster, it summarizes

each cluster in a way that we can use it for pattern

extraction, pattern matching, and pattern merging.

Moreover, this model is able to classify new objects.

Using GMM, each new test sample is fed into the

GMM of a cluster, and if the membership

probability to a cluster is more than a threshold, the

object is attached to that cluster.

The structure of the paper is as follows: In Section 2,

we review related work on arbitrary shape clusters

and summarization approaches. In Section 3, we

explain the general structure of the proposed

algorithm for summarization. In Section 4, we

present some discussions about the features of the

proposed method. In Section 5, we explain the

complexity of algorithm in more detail. Section 6

presents the experimental results of the proposed

algorithm in comparison with well-known

summarization algorithms. Finally, the conclusion

and future work are presented in Section 7.

2 RELATED WORK

There are various algorithms available for clustering,

which are categorized into four groups; partition-

based, hierarchical, density-based and spectral-based

clustering (Han, 2006). K-means is one of the

famous algorithms in the area of partition-based

clustering. However, using a centre and radius

makes the shape of clusters spherical which is

undesirable in many applications. In hierarchical

clustering methods such as Chameleon data is

clustered in hierarchical form but still with spherical

shape that is undesirable. Moreover, tuning the

parameters for methods like Chameleon is still

difficult (Karypis et al., 1999). Spectral clustering;

STING (Wang et al., 1997) and CLUIQE (Agrawal

et al. 1998) are able to create arbitrary shape clusters

but the major drawback of these methods is the

complexity of creating an efficient grid. The size of

grid varies for different dimensions and setting

different grid sizes and merging the grids to find

clusters are difficult. These difficulties make the

algorithm inaccurate in many cases. In the area of

arbitrary shape clustering, density-based methods

are more interesting and DBSCAN (Ester et al.,

1996) and DENCLUE (Hinneburg et al., 1998) are

the most famous ones. In density-based methods,

clusters are created using the concept of connecting

dense regions to find arbitrary shape clusters. Based

on prevalence of real time applications, there is more

interest to make these algorithms fast for streaming

applications (Guha et al., 2003)(Bifet et al.,

2009)(Charu et al., 2003).

Summarization is the solution to ease the complexity

of arbitrary shape clustering methods. The naïve

way to represent an arbitrary shape cluster is to

represent each cluster with all cluster members.

Obviously, this approach is neither practical nor

does it reflect the cluster properties. In k-means a

simple representation using a centre and radius

summarize the cluster. It is clear that this

summarization does not capture how data is

distributed in the cluster.

There are different ways to summarize arbitrary

shape clusters (Yang et al., 2011)(Cao et al.,

2006)(Chaoji et al., 2011). These algorithms use the

general idea behind the clustering methods for

arbitrary shape clusters. In the area of

summarization, the idea is to detect dense regions

and summarize the regions using core objects. Then,

a set of proper features is considered to summarize

the dense regions and their connectivity. In (Yang et

al., 2011) a grid is created for each cluster and based

on the idea of connecting dense regions, the core or

dense cells with their connections and their related

features are kept. In all summarization approaches,

these features play crucial role. In (Yang et al.,

2011) location and range of values and status

connection vector are kept however, it has some

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

draw backs. First, creating grids on each cluster is

time consuming. Second, considering all grids needs

spending a lot of time and space which is impractical

in many cases. Cao et al. (Cao et al., 2006) use the

idea of finding core objects to generate the cluster

summery. The most significant drawback of this

work is that the number of core objects is large and

in some cases, it is equal to the number of input

samples. Moreover, a fixed radius specifies the

neighbourhood that does not represent the

distribution of objects in each cluster (Cao et al.,

2006). Chaoji et al. represent a density-based

clustering algorithm named ABACUS for creating

arbitrary shape clusters (Chaoji et al., 2011). The

summarization part in their approach is based on

finding the core objects and the relative variance

around the objects. In most of arbitrary shape

clustering methods, we need two parameters;

number of neighbours and a radius. The most

interesting and noticeable part in Chaoji et al. work

is that the number of neighbours is the only

parameter for their algorithm and they generate

radius using data distribution. The significant

drawback in their work is that the algorithm may

generate many core points.

In all above mentioned summarization approach,

focus is on preserving the cluster members and they

don’t consider any usage of clustering for

classification purpose. Clustering approaches are

created to summarize data and categorized the input

data into some groups, but it can also be used as a

pre-processing phase of classification task (Ester,

1996)(Hinneburg, 1998). Each cluster has a label

and for each new object the closest cluster is found

and the object gets the label of that cluster. The

mentioned approaches like k-means summarize the

clusters, but they still consider the concept of circles

around the core objects to find the closest cluster

which is inaccurate. Graph-based structures are more

accurate but they are time consuming. Anomaly

detection is one of the applications of clustering in

classification (HE, 2003)(Borah and Bhattacharyya,

2008)(Gaddam, 2007)(Mohammadi, 2014). In this

area, those objects which are outside of cluster

boundaries are considered as anomaly. In previous

works, clusters are generated using k-means and

summarized with a centre and a radius which is

inaccurate.

In this paper, we present an approach to summarize

clusters using Gaussian Mixture Models. Our

approach covers both areas; it is a good

representative of a cluster and it can be used for

classification purpose.

3 GENERAL STRUCTURE OF

THE SGMM ALGORITHM

The main idea behind the density-based clustering

algorithms is to connect dense regions to create a

cluster. With this idea, a set of core objects are

detected and they are connected to each other using

the shared neighbourhood.

DEFINITION 3.1. In dataset D for a given k and

radius r, an object 



is a core object if

∀x ∈ D, o



∈Cdo

,

,xk

Where C is set of core objects and (

‖



‖

shows the

number of objects with distance less than r from the

core object. Detection of k and r is critical in

identifying good clusters.

Figure 1: Structure of the SGMM method for cluster summarization.

The

original

Cluster

Finding

Core

Points

Feature

Extractio

Absorptio

GMM

Extractio





,Σ



,





,Σ



,





,Σ



,





,Σ



,





,Σ



,

ArbitraryShapeClusterSummarizationwithGaussianMixtureModel

The concept of core objects has been used to

generate the backbone of a cluster and generate

summery of the cluster. In some recent works

(Chaoji, 2011) using a given k and core objects idea,

they detect the backbone of cluster. In this paper, we

use the same idea but with more concentration on

decreasing the number of core objects and the time

of detection of these core objects. The general idea

for summarization of each cluster in this paper is

based on Gaussian Mixture Model. Since Gaussian

Mixture Model preserves the distribution of data

using a set of Normal Distributions, it is a good

candidate for summarizing any cluster. Therefore,

we can apply simply EM algorithm on each cluster

to find its GMM representative, but the main

concern is to find the number of GMM components.

In our proposed approach, we first find the number

of GMM components, and then we find appropriate

GMM for each cluster. Our method, Summarization

Based on Gaussian Mixture Model (SGMM), has

four main steps that are depicted in Figure 1. First, a

set of objects called core objects are detected. These

objects are representative of a cluster and can

generate the original cluster as needed. After

detection of backbone objects, there comes the

absorption step, where the objects attached to the

core object are absorbed and represented by core

objects. Then by introducing a new feature set for

each object, cluster is summarized while its original

distribution is preserved. Finally, each cluster is

presented as a GMM. In the following sections, we

describe each step in more detail.

3.1 Finding Core Objects

In this step, we find the core objects that create the

backbone of each cluster. There are different ways to

find the core objects in each cluster, but time is the

main concern in this case. In this step, we consider a

radius based on which we find the neighbours for all

objects for each cluster. Then we sort all objects

based on the number of neighbours. The first core

object is the one with the maximum number of

neighbours. All the neighbours of this object are

removed from the list of possible core objects. With

this approach, we reduce the overlap of core objects

as much as possible. Among the remaining objects,

we find the next objects with maximum number of

neighbours. We label this object as a core object and

remove neighbours of this object from further

consideration. In this way with a heuristic approach,

we find the core objects located in dense regions and

all parts of cluster are covered using them. The new

definition of the core objects with our methodology

is presented as follow.

DEFINITION 3.1.1. (Core Object) A core object is

the object that has the maximum number of

neighbours in comparison with other objects in its

neighbourhood. The core object is not in the

neighbourhood of another core object.

∀c



∈Cij,dc





r

Where i and j are the index for different core points

and d refers to the distance of two objects.

3.2 Absorption and Cluster Feature

Extraction

The goal of summarization is to find a good

representative of each cluster and core objects are

the only objects that we preserve in each cluster

while the rest of the objects in the cluster are

removed. After finding all core objects in each

cluster, the next step is to define a cluster using core

objects. It is obvious that considering only core

objects cannot be a good representative of each

cluster. The core objects have to be accompanied

with a set of features related to the cluster to

represent a cluster. This is why we define a set of

features for each core object which are good

representative for distribution around each core

object.

DEFINITION 3.2.1: (Core Object Feature) (CF)

Each core object is represented by a triple

〈





,



,



〉

In this definition 



is the core object and Σ



is the

covariance calculated using the core object and all

objects in its neighbourhood. 



/ is the

weight of core object, n is the number of objects in

the neighbourhood of core object 



, and CS is

cluster size. 



shows the proportion of objects

which are in the neighbourhood of the core object.

Using the features for each core object, we estimate

samples scattering around each core object without

keeping the entire samples in the neighbourhood.

3.3 GMM Representation of Clusters

After finding the core objects and all necessary

features for each cluster, we generate a Gaussian

Mixture Model for each cluster.

DEFINITION 3.3.1. A Gaussian Mixture Model is a

combination of a set of normal distributions. Given

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

feature space ⊂



, a Gaussian Mixture Model

: →  with n component is defined as:

)()(

xwxg

i 









iii

)()(

)2(

)(

















(1)

Based on all 



,   1 ⋯  , a GMM is defined

over a cluster. Each component for GMM is created

using a core object, its covariance and the weights.

In the formula in equation (1), μ



is the centre of the

GMM component, which is set to the coordination

of core object and therefore, μ



c



. The covariance

is set to covariance of i

core object covariance, that

is Σ



. The weight for each component is the weight

of core object and as a result w



in the equation (1) is

set to the weight of core object c



which is ω



The main goal of cluster summarization is to present

a cluster in a way that it keeps the overall

distribution of the cluster while reducing the number

of objects in the cluster which is critical in stream

data mining and online environment. To use a

cluster as a class in classification, we need to find

the closest cluster to a new incoming sample. In an

arbitrary shape cluster, all objects represent a cluster

and to find a right cluster for a new sample, it has to

be compared with all objects in a cluster. GMM-

based summarization fulfils both requirements for

both applications; summarize data for the real time

applications; generate a proper representation for

each cluster to use them in classification approach.

4 GAUSSIAN MIXTURE

SUMMARIZATION

As each GMM consists of a set of Gaussian

distributions, finding the number of GMM

components is a challenging issue. In this paper, we

proposed a solution to calculate number of

components for each cluster by finding the core

points. In our approach, number of components for

GMM is set to the number of core objects in a

cluster.

There are two essential features that should be

considered. Each summarization technique has to

preserve the original shape and the distribution of

the data. Summarization of data using GMM has

both characteristics. In SGMM some objects are

selected in a way that they follow the general

structure of data. Not only finding the core object is

easy and fast but also it still follows the shape of the

cluster. The algorithm starts from dense regions in

the cluster and then goes to the most scattered part

with consideration of covering all data objects in the

cluster. In the SGMM method, the core objects are

the ones which are in the center of dense regions and

they cover all data. Therefore, for each region a

representative object is chosen and then collection of

these representative objects presents the entire

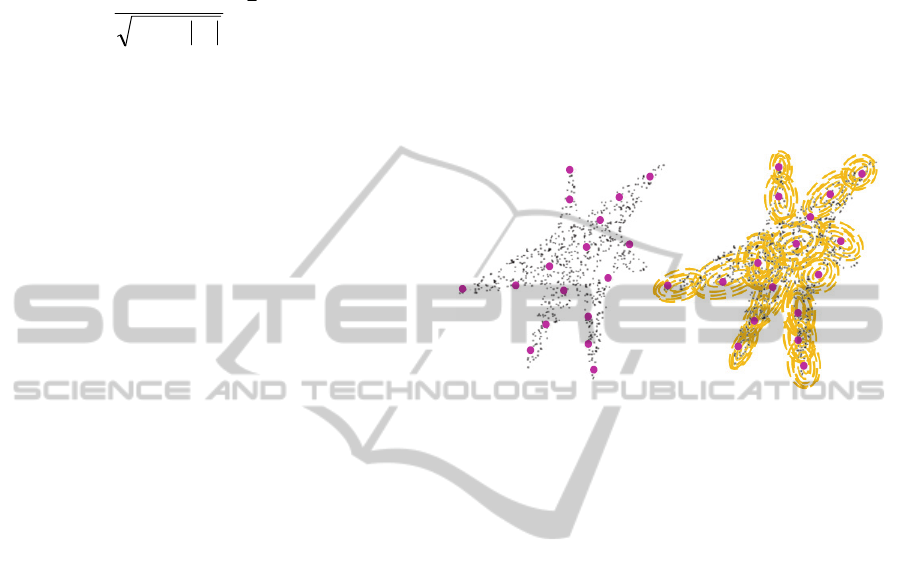
cluster. Figure 2, shows the core objects generated

for a cluster. This figure shows that the generated

core objects follow the general structure of the

cluster.

Figure 2: Cluster with the core objects.

Finding the general structure of a cluster using a set

of objects is not enough for achieving high accuracy

in classification applications. In many applications,

we would like to keep the original or summery of

data for more detail investigation. Saving the core

objects cannot reveal any information about the

distribution of data. Therefore, we need to find

distribution information around the core objects and

as we mentioned above, we capture such

information using the covariance around core

objects. Using such information, we are able to

regenerate the original data.

Finally, we need to know the contribution of each

core object in generation of data. We find out the

weight of each core object based on the number of

neighbours that each object has. With knowing the

location of core objects, related covariance and the

weights, we summarize data using a GMM with the

minimum loss of information. The relative GMM for

a cluster is depicted using contour plots in Figure 2.

5 COMPUTATIONAL

COMPLEXITY

In stream data mining application, using a fast

algorithm is a critical requirement. In this section,

we examine the computational complexity of the

proposed algorithm.

ArbitraryShapeClusterSummarizationwithGaussianMixtureModel

In the first step of algorithm, we find the neighbours

of each object; with N as the number of objects it

takes

O(



)

to find neighbours. Then, we need to

sort the objects and absorb neighbours of the core

objects that takes O(NlogN). In absorbing step, we

find the number of neighbours for each core object

and its related variance. We consider O(NlogN) for

the second part of the proposed method which is the

worst case.

So, the final complexity of the proposed algorithm is

O(



)

. In the grid-based method a

considerable amount of time is spent to create the

grid and further investigation to find core grids and

connecting them. In some other density-based

methods such as ABACUS there are iterations to

find core objects and to reallocate them which are

time consuming. The output of SGMM is almost the

same as that of ABACUS but the proposed method

is not time consuming in comparison to ABACUS.

The experiment results show that our heuristic leads

to the same result with one step. In the next section,

we develop a comparison between the required time

of our method and the one for ABACUS. The results

illustrate that the proposed method outperforms

ABACUS in term of time.

6 EXPERIMENTAL RESULTS

We use both synthetic data set and the real data set

in our experiments. Time and space complexity and

the goodness of clustering are three different criteria

that we evaluate our algorithm based on. Moreover,

we set up different experiments to see the efficiency

of our algorithm for categorizing new samples. We

compared our algorithms with ABACUS (Chaoji,

2011) which is one of the well-known

summarization methods in literatures. All

experimental results are generated in Matlab running

on a machine with Intel CPU 3.4 GHz and 4GB

memory.

The first data set is a synthetic dataset as shown in

Figure (3). We use this dataset to visualize the

effectiveness of the proposed algorithm.

Figure 3: Synthetic data with related GMMs.

This figure shows 4 clusters and set of objects used

in testing phase. In this Figure we see each cluster is

represented by a GMM depicted with a contour plot.

KDD dataset and some other UCI datasets are

considered in our experiments to evaluate the

accuracy of our algorithm on some real datasets.

6.1 Clustering Goodness

To show the efficiency of SGMM method, we set up

experiments in which we summarize the dataset

using core objects then we used these core objects

and their related variance and weights to regenerate

the dataset. The difference between the first dataset

and regenerated dataset by core objects shows the

strength of summarization algorithm. Experimental

results show that SGMM method summarize dataset

better than ABACUS method. To visualize the

results, we generated a synthetic data with four

clusters. Figure 4 from left to right shows the

original dataset, core objects of each cluster and the

dataset set regenerated using core objects using

ABACUS and SGMM method. This figure shows

that the core objects follow the original structure of

the clusters and the regenerated clusters are similar

to the original ones. This figure depicts the ability of

SGMM method, and it shows that the summery

generated by SGMM regenerates the original dataset

better in comparison to ABACUS method. The

difference between the accuracy of summarization

of ABACUS and SGMM is clearer in the cluster

with star shape. SGMM summery regenerate the

data with star shape, but ABACUS method could not

regenerate the same shape. These figures are just for

visualization the result and to show the efficiency of

the algorithm, we use Dunn and DB index.

The Dunn index (Dunn, 1979) is a validity index

which identifies compact and well-separated classes

defined by equation (2) for a specific number of

classes:

1,..., 1,...,

1,...,

(, )

min min

max ( )

incjinc

knc

dist c c

diam c

























Where nc is the number of classes, and dist(c

) is

the dissimilarity function between two classes C

and

. The large values of the index indicate the

presence of compact and well-separated classes. In

our experiments, we first calculate the Dunn index

for the original datasets. Then, summarize the

dataset and re-generate the data again using the final

core objects of GMMs and we find out the Dunn

index for regenerated data. Finally, we get the

difference between Dunn index of original dataset

(2)

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

Figure 4: The first dataset is the original dataset, the second one is the core points and the third one is regenerated dataset

using the core points based on ABACUS and SGMM methods.

and the one which is regenerated. Using this

experiment, we want to evaluate the regeneration

ability of the SGMM method. In other words, we

want to show how the SGMM method regenerates

the data which follows the shape and distribution of

the original data. Table 1 shows the results of this

experiment. Each value in this table is the average of

30 independent runs.

Table 1: Difference of Dunn Index for original and

regenerated dataset.

Dataset\Index SGMM ABACUS

Synthetic Data

0.02358 0.076932

KDD

0.027701 0.034321

Segment

0.008841 0.014636

The closer the value to zero, the better the result we

get. Based on the difference of Dunn index table,

SGMM always outperforms ABACUS by far. For

example in case of Segment dataset, the difference

between the dataset generated by SGMM and the

original dataset is almost zero while this value for

ABCUS is around 0.01. This experiment illustrated

that SGMM follow the sample distribution of the

original dataset better than ABACUS. The next step

is to repeat the experiment using DB cluster index.

The second measurement we used is DB index

(Davies and Bouldin, 1979) which is a function of

the ratio of the sum of within cluster scatter to

between-cluster separation. DB index is defined as

in equation (3).























jin

jnin

QQS

QSQS

),(

)()(

max

(3)

n is the number of clusters,





is the average

distance of all objects of the cluster to their cluster

centre, and









,





is the distance between clusters

centres. Hence, the ratio is small if the clusters are

compact and far from each other. Consequently,

Davies-Bouldin index will have a small value for a

good clustering. As what we did for Dunn index, we

find the distance of the original and regenerated

data. Table 2 shows the experimental results of DB

index on different datasets.

Table 2: Difference of DB Index for original and

regenerated dataset.

Dataset\Index SGMM ABACUS

Synthetic Data

0.006638 0.017609

KDD

0.195763 0.232498

Segment

0.0429764 0.0546819

Result based on Dunn and DB index shows that the

SGMM method generates more accurate summery

of dataset and in case of regenerating the original

dataset SGMM follows the original pattern better.

Original Dataset Core points Regenerated Dataset

SGMM

ABACUS

ArbitraryShapeClusterSummarizationwithGaussianMixtureModel

6.2 Clustering Accuracy

As mentioned above, clustering is used in

classification as a preprocessing step. The

application we focused on, in this part, is anomaly

detection. We first cluster the normal data into some

clusters then we consider these clusters as normal

behaviours. The membership probability for each

new sample is calculated. If the sample belongs to a

cluster, it is normal otherwise it is an attack. For this

purpose, we consider KDD dataset and we find out

the accuracy of attack detection. Using GMM in

classification is our proposed method and to the

knowledge of author there is no other work similar

to our approach. The only approach that has been

used in an arbitrary shape cluster to label new

sample is to consider all member of clusters which is

the Naïve approach. In our experiment, we created

GMM using our set of core objects and ABACUS

core objects. As we mentioned, we created the core

objects using a simple method that spends less time

and space. Therefore, there can be a doubt about the

accuracy of categorizing using the clusters using our

method? The experiment shows that our approach

does not decrease the accuracy.

The ROC curve based on detection rate and false

alarm rate for KDD dataset depicted in Figure 5. It

shows while the ABACUS is more time consuming

and find out too many core objects our method has

the same and sometimes better accuracy. Figure 6

shows the result for synthetic dataset. It shows that

the accuracy of our approach is better than Naïve

and ABACUS method. The result for synthetic

dataset set shows that in spite of using clustering in

categorizing new objects the accuracy is still good

and comparable to the accuracy of classification

methods.

Figure 5: ROC curve for KDD dataset.

Figure 6: ROC curve for Synthetic dataset.

Table 3 shows more results on some other datasets,

which confirms that summarizing and clustering

data using SGMM method outperforms ABACUS

method. The first value in Table 4 is the false alarm

rate and the second one is the detection rate.

Table 3: Accuracy of SGMM and ABACUS method in

anomaly detection.

Dataset\Index SGMM ABACUS

Synthetic Data

(2,94) (1.9,87)

KDD

(6.301, 100) (9.041, 100)

Segment

(33.83,94.39) (32.82,94.54)

6.3 Algorithm Complexity

Two main concerns in the area of summarization are

the time spent to find the summery of a cluster and

the number of objects preserved for it. Table (4)

shows the space and the time spent to find the

summery of a cluster for different datasets. This

table shows that SGMM decreases time and space to

summarize each cluster. It is clear that SGMM

method uses only one iteration to find core objects

while ABACUS method runs many iterations to find

out the core objects and therefore, SGMM is faster.

On the other side, SGMM summarizes cluster with

less number of core objects. The reason lies in the

SGMM algorithm in finding core objects. If an

object is core object, all objects in its neighborhood

are removed from possible set of core objects and

we do not consider them. In this case, we are able to

decrease the time and space complexity both. Table

4 and 5 shows the time and space used by SGMM

and ABACUS and it shows that using SGMM we

decrease time and space considerably.

100

0 20406080100

Detection Rate

False Alaram Rate

KDD

SGMM

ABACUS

Naïve Approach

100

0 20406080100

Detection Rate

False Alarm

Synthetic data

SGMM

ABACUS

Naive

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

Table 4: Number of core objects for ABACUS and

SGMM methods.

Dataset\Space

complexity

SGMM ABACUS

Synthetic Data 51 120

KDD 46 272

Segment 52 55

Table 5: The time complexity for ABACUS and SGMM

methods.

Dataset\Time

complexity

SGMM ABACUS

Synthetic Data 388 sec 1261 sec

KDD 222 sec 836 sec

Segment 7 sec 19 sec

7 CONCLUSIONS

In this paper, we presented a new approach for

summarizing the arbitrary shape clusters. Our

proposed algorithm, named SGMM, represents each

cluster by a Gaussian Mixture Model (GMM) using

sets of core objects. Each GMM is a representative

of the distribution of whole members in a cluster.

Moreover, SGMM is able to find the closest cluster

for each new incoming sample. The experimental

results based on Dunn and DB index confirms that

the distribution of clusters is preserved after

summarization. Additionally, in case of

classification, the accuracy using SGMM is

acceptable. Our proposed algorithm also exhibits a

low computational cost which makes it a suitable

approach for clustering stream data. Extending the

density based clustering to make it faster is a part of

our future work.

REFERENCES

Agrawal, J. Gehrke, D. Gunopulos, and P. Raghavan,

1998, “Automatic sub-space clustering of high

dimensional data for data mining applications,”

SIGMOD Rec, vol. 27, pp.94–105.

Bifet, A, Holmes G, Pfahringer B 2009. New ensemble

methods for evolving data streams. In: Proceedings

ofthe 15th ACM SIGKDD international conference on

knowledge discovery and data mining. pp 139–148.

Borah B., Bhattacharyya D., 2008. Catsub: a technique for

clustering categorical data based on subspace. J

Comput Sci2:7–20.

Charu C. Aggarwal , T. J. Watson , Resch Ctr , Jiawei Han

, Jianyong Wang , Philip S. Yu, 2003, A framework

for clustering evolving data streams. Proceedings of

the 29th VLDB Conference, Berlin, German.

Davies D.L.,. Bouldin D.W. A cluster separation measure.

1979. IEEE Trans. Pattern Anal. Machine Intell. 1 (4).

Pp. 224-227.

Yang D, Elke A, , Matthew O. Ward. 2011,

Summarization and Matching of Density-Based

Clusters in Streaming Environments. Proceedings of

the VLDB Endowment (PVLDB), Vol. 5, No. 2, pp.

121-132.

Ester. M., Kriegel. H., Sander. J., and Xu. X. 1996, A

density-based algorithm for discovering clusters in

large spatial databases with noise. In KDD, pages

226–231.

Cao F, Ester M, Qian W, Zhou A, Density-based, 2006,

clustering over an evolving data stream with noise. In

2006 SIAM Conference on Data Mining. 328—339.

G. Karypis, E.-H. Han and V. Kumar, 1999, Chameleon:

Hierarchical Clustering Using Dynamic Modeling,

Computer, 32:8, pp. 68–75.

Gaddam S, Phoha V, Balagani K., 2007, K-means+id3: a

novel method for supervised anomaly detection by

cascading k-means clustering and id3 decision tree

learning methods. IEEE Trans Knowl Data Eng

19(3):345–354.

Guha S, Meyerson A, Mishra N et al, 2003, Clustering

data streams: theory and practice. IEEE Trans Knowl

Data Eng 15(3):505–528.

Han. J, Kamber. M, J. Pei. 2006. Data Mining: Concepts

and Techniques, Third Edition (The Morgan

Kaufmann Series in Data Management Systems).

HE, Z., XU, X., AND DENG, S. 2003. Discovering

cluster-based local outliers. Pattern Recog. Lett. 24, 9–

10,1641–1650.

Hinneburg. A. and Keim. D. A. 1998. An efficient

approach to clustering in large multimedia databases

with noise,” in KDD , , pp. 58–65.

John Hershberger, Nisheeth Shrivastava, Subhash Suri,

2009. Summarizing Spatial Data Streams Using

ClusterHulls, Journal of Experimental Algorithmics

(JEA), Volume 13,. Article No. 4 ACM New York,

NY, USA.

K. Dunn, j. Dunn. Well separated clusters and optimal

fuzzy partitions. Journal of Cybernetics ,(4), (1974),

pp. 95-104.

Kristian Kersting, Mirwaes Wahabzada, Christian

Thurau, Christian Bauckhage., 2010. Hierarchical

Convex NMF for Clustering Massive Data. ACML:

253-268.

Mohammadi M, Akbari A, Raahemi B, Nasersharif B,

Asgharian H. 2014. A fast anomaly detection system

using probabilistic artificial immune algorithm capable

of learning new attacks. Evolutionary Intelligence

6(3): 135-156.

Chaoji V, Li W, Yildirim H, Zaki M, 2011. ABACUS:

Mining Arbitrary Shaped Clusters from Large

Datasets based on Backbone Identi

ﬁcation. SDM,

page 295-306. SIAM / Omnipress,.

Wang. W., Yang. J., and Muntz. R. R., 1997. Sting: A

statistical information grid approach to spatial data

ArbitraryShapeClusterSummarizationwithGaussianMixtureModel

mining. In Proceedings of the 23rd International

Conference on Very Large Data Bases ,ser.VLDB’97.

San Francisco, CA, USA:Morgan Kaufmann

Publishers Inc., pp.

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval