
Concurrent Optimization of Flight Distance and Robustness of
Equipment and Skills in Discus Throwing
Kazuya Seo and Kana Takaoka
Department of Education, Art and Science, Yamagata University, 1-4-12 Kojirakawa, Yamagata, Japan
Keywords: Sports Engineering, Discus, Equipment, Skills in Sports, Robustness, Flight Distance.
Abstract: This paper describes the concurrent optimization of flight distance and ‘robustness’ of the equipment and
skills in a discus. Two objective functions are considered. One is the flight distance, and the other is
robustness. Robustness is defined as insensitivity to deviations from the local optimal release conditions.
The aim of the optimization is to maximize both the flight distance and the robustness. Fourteen design
variables are considered. Eight of the fourteen are concerned with the skill of the thrower. They determine
the launch conditions, which are controlled by the thrower when he or she throws. The other six variables
are concerned with the design of the equipment. These are the dimensions of the discus, the moment of
inertia about the transverse axis and finally the mass of the discus. The dependences of size and the angle of
attack on the aerodynamic data are estimated by using CFD (computational fluid dynamics) technique. It
was found that there is a trade-off between flight distance and robustness. The flight distance is 78.8 meters
at the sweet spot solution, where both objective functions have better values simultaneously. The stalling
angle for the sweet spot solution is relatively high.
1 INTRODUCTION
Discus throwing is a sport in which the thrower
attempts to gain the longest flight distance. In this
study, two objective functions are considered (Multi-
objective optimization (Deb, 2001)). One is the
flight distance, and the other is the robustness. There
are fourteen design variables that are considered,
including the release conditions (skills), sizes of the
discus, the mass and the moment of inertia of the
discus (equipment).
Flight distance has usually been treated as the
only objective function in the optimization of the
discus so far (Hubbart and Cheng, 2007). Generally,
it is considered that there are many local longest
flight distances (= local optimal solutions) with
respect to the design variables. Some of local longest
flight distances are sensitive to changes in the design
variables. This sensitivity is a difficult problem for
throwers. The thrower sometimes makes mistakes
when trying to achieve the global optimal release
condition. The thrower is not a robot, but a human.
Therefore, robustness is also important, especially
for the world of competitive sports. Here, robustness
can be defined as insensitivity to deviations from the
local optimal release conditions.
2 FLIGHT TRAJECTORY
2.1 Inertial Coordinate System
The inertial coordinate system is shown in Figure 1.
The origin is defined as being at the center of the
throwing circle, while the X
E
-axis is in the horizontal
forward direction, the Y
E
-axis is the horizontal
lateral direction and the Z
E
-axis is vertically
downward.
2.2 Body-fixed Coordinate System
The coordinate system in the discus body-fixed
system is denoted by x
b
, y
b
and z
b
(Figure 2-c). The
origin is defined as the center of gravity of the
discus. It is assumed that the geometric center of the
discus coincides with the center of gravity, that its z
b
axis is aligned with the transverse axis (axis of
symmetry), and that x
b
and y
b
are aligned with the
longitudinal axes in the discus planform. Assuming
that the origin of the inertial coordinate system (X
E
,
Y
E
, Z
E
) is displaced without any rotation to the center
of gravity of the discus, the new reference frame is
defined as (X
0
, Y
0
, Z
0
) in Figure 2-a. The sequence of
198
Seo K. and Takaoka K..
Concurrent Optimization of Flight Distance and Robustness of Equipment and Skills in Discus Throwing.
DOI: 10.5220/0005071601980206
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 198-206
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
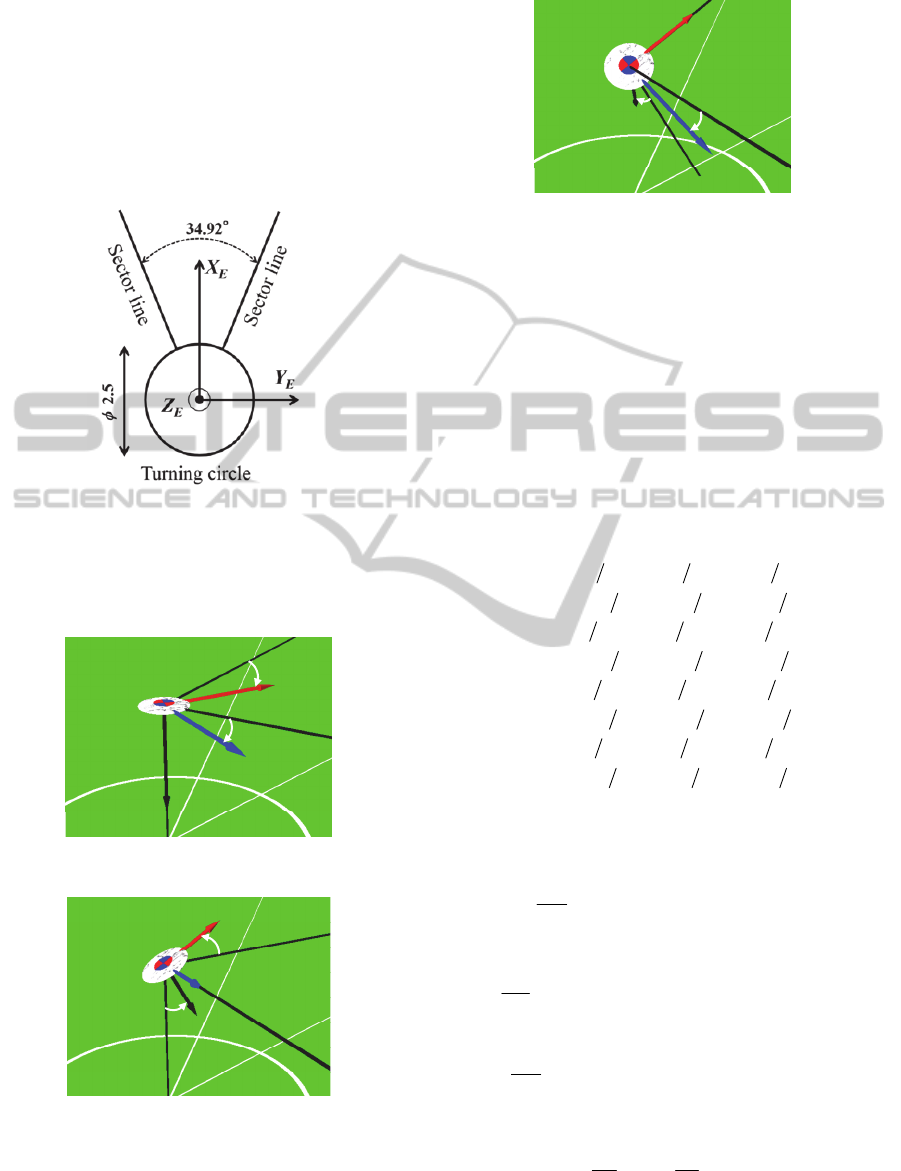
rotations conventionally used to describe the
instantaneous attitude with respect to an inertial
coordinate system is shown in Figure 2 (Stevens and
Lewis, 2003). Starting with (X
0
, Y
0
, Z
0
) the following
sequence is followed; 1) Rotate about the Z
0
axis,
nose right (positive yaw Ψ, Figure 2-a), 2) Rotate
about the y
1
axis, nose up (positive pitch Θ, Figure
2-b), 3) Rotate about the x
b
axis, right wing down
(positive roll Φ, Figure 2-c).
Figure 1: The inertial coordinate system. The origin is
defined as being at the center of the turning circle, while
the X
E
-axis is in the horizontal forward direction, the Y
E
-
axis is the horizontal lateral direction and the Z
E
-axis is
vertically downward.
Figure 2-a: Definition of Ψ.
Figure 2-b: Definition of Θ.
Figure 2-c: Definition of Φ.
Figure 2: Definitions of Euler angles that are used to
describe the instantaneous attitude with respect to the
inertial coordinate system.
2.3 Flight Trajectory Simulation
Since there is a mathematical singularity (Gimbal
lock) at Θ= 90°, quaternion parameters (q
0
, q
1
, q
2
,
q
3
) should be used instead of Euler angles when the
flight trajectory is simulated. Therefore, the initial
set of Euler angles is first transformed into the initial
quaternion parameters by Equations (1) through (4)
(Stevens and Lewis, 2003).
2sin2sin2sin
2cos2cos2cos
0
q
(1)
2sin2sin2s
2cos2cos2sin
1
co
q
(2)
2sin2s2sin
2cos2sin2s
2
co
coq
(3)
2s2sin2sin
2sin2s2s
3
co
cocoq
(4)
The force equations and moment equations of
motion in the discus body-fixed system are denoted
by Equations (5) through (10).
RVQW
qqqqgmX
m
U
da
d
2031
2
1
(5)
PWRUqqqqgmY
m
V
da
d
1032
2
1
(6)
QUPV
qqqqgmZ
m
W
da
d
2
3
2
2
2
1
2
0
1
(7)
1
L
T
L
a
I
I
QR
I
L
P
(8)
z
2
y
2
x
2
x
b
z
b
y
b
z
1
y
1
x
1
z
2
y
2
x
2
X
0
Y
0
Z
0
z
1
y
1
x
1
ConcurrentOptimizationofFlightDistanceandRobustnessofEquipmentandSkillsinDiscusThrowing
199

L
T
L
a
I
I
RP
I
M
Q 1
(9)
T
a
I
N
R
(10)
Here, (
U, V, W), (P, Q, R), (X
a
, Y
a
, Z
a
) and (L
a
, M
a
,
N
a
) are the (x
b
, y
b
, z
b
) components of the velocity
vector, the angular velocity vector, the aerodynamic
forces and the aerodynamic moments, respectively.
The mass of the discus is denoted by
m
d
, and the
gravitational acceleration is denoted by g. The
moments of inertia about the transverse axis and the
longitudinal axis are denoted by
I
T
and I
L
. Due to the
symmetry of the discus, the principal moments of
inertia on the
x
b
and y
b
axes are set to I
xx
=I
yy
= I
L
in
Equations (8) through (10), and the cross inertia
terms are zero. The aerodynamic forces (
X
a
, Y
a
, Z
a
)
and moments (L
a
, M
a
, N
a
) are derived from C
D
, C
L
and
C
M
on the basis of the cross product (Seo, et al,
2010). Aerodynamic coefficients, C
D
, C
L
and C
M
are
estimated by using CFD (computational fluid
dynamics) technique, which will be described in the
next section. Other aerodynamic coefficients are
assumed to be 0.
The derivatives of the quaternion parameters are
expressed by the angular velocity vector (
P, Q, R)
(Stevens and Lewis, 2003).
3210
5.0 RqQqPqq
(11)
2301
5.0 RqQqPqq
(12)
1032
5.0 RqQqPqq
(13)
0123
5.0 RqQqPqq
(14)
In terms of coordinate transformations we then have
W
V
U
m
Z
Y
X
ij
E
E
E
(15)
Here, [
m
ij
] is the Euler-angle transformation matrix
(Stevens and Lewis, 2003). The flight trajectory
(
X
E
(t), Y
E
(t), Z
E
(t)) can be obtained by integrating
Equations (5) through (15) numerically.
3 ESTIMATING AERODYNAMIC
COEFFICIENTS
3.1 CFD
In order to understand the dependence on the size of
the discus of the aerodynamic forces, it is necessary
to study many discuses of various sizes. In this
study, the CFD technique was applied to estimate
the aerodynamic forces.
A discus was initially developed using Ansys
DesignModeler. It had the same width (
w) of
181.5mm, thickness (THK) of 37mm, metal rim
radius (
R
MR
) of 6.15mm and diameter of the flat
center area (D
FCA
) of 50mm as the competition
discus (Super HM, Nishi Athletics Goods). A cube
in which all 12 edges are 4000mm, was constructed
around the discus as an enclosure. The frontal area
of the cube was defined as a velocity inlet, while the
rear of the cube was set as a pressure outlet where
the airflow exits. The rest of the boundaries were
defined as walls. These were then imported to Ansys
Meshing, a pre-processor of CFD code FLUENT.
Hybrid meshes of tetrahedrons and hexagons were
used. The size function and the inflation controls
were also used to mesh the volumes. If the number
of cells were more than one million, then the
aerodynamic coefficients determined by CFD would
agree with those determined by EFD. However, the
computing time for CFD is more than three hours for
just one case. Here, there are hundreds of cases to be
calculated. Since the computing time is also
important, the number of cells was set 213,314 by
local inflation settings. It takes about 30 minutes to
estimate aerodynamic coefficients (Core i7-960,
3.2GHz, 6 cores). In this case, the values of (
C
D
, C
L
,
C
M
) = (0.23, 0.71, 0.18) at AoA=25° and 30ms
-1
are
almost same as those (
C
D
, C
L
, C
M
) = (0.23, 0.74,
0.18) determined by the fine mesh (1,171,589 cells).
The average skewness in the case of 213,314 cells
was 0.25. The growth rate was 1.2.
The aerodynamic forces in the steady flow state
were calculated by FLUENT 14.0. Comparisons
between EFD and CFD at
AoA=25° and 30ms
-1
are
shown in Figure 3. The ordinates are the ratio
between CFD and EFD. If CFD/EFD is equal to 1,
the aerodynamic coefficients derived by CFD
coincide with those obtained by EFD. The abscissa
shows four combinations of RANS-based turbulence
model and wall treatments. It can be seen that
C
D
and
C
L
derived by CFD are all smaller than those
derived by EFD. The combination of the standard k-
epsilon (ske) model and the enhanced wall treatment
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
200
(ewt) gives the best agreement with EFD, though
C
M
derived by CFD is 20% larger than that by EFD.
Moreover, the standard k-epsilon model is robust.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
ske+swf rke+swf ske+ewt RNG+ewt
C
D
C
L
C
M
CFD/EFD
Figure 3: Comparisons of aerodynamic coefficients
between CFD and EFD. AoA=25 and U=30 ms
-1
.
ske=standard k-epsilon, rke=realizable k-epsilon,
swf=standard wall function, ewt=enhanced wall treatment.
Therefore, the standard k-epsilon model with the
enhanced wall treatment was used for the turbulence
modelling. The second-order upwind method was
selected for all equations, and the convergence
criterion for continuity equations was set as 10
-3
.
3.2 Comparison between EFD
(Experimental Fluid Dynamics)
Results and CFD Results
Comparisons between the EFD results and the CFD
results is shown in Figure 4. The aerodynamic
coefficients,
C
D
, C
L
and C
M
, as a function of AoA are
shown. The definition of the drag coefficient, C
D
, is
the drag divided by the dynamic pressure and the
area of the discus planform. The lift coefficient,
C
L
,
and the pitching moment coefficient,
C
M
, are defined
in the same manner. Since there is little difference
between aerodynamic coefficients for wind speeds
in the ranges from 15 to 30 ms
-1
and from 0 to 7
revolutions per second (Seo et al., (2012)), the data
at 30 ms
-1
and 0 revolutions per second are shown
with error bars. The open circles denote EFD results
from wind tunnel tests during the process of
increasing
AoA from 0° to 90°, while the open
triangles show the process when decreasing AoA
from 90° to 0°. The closed diamonds show CFD
results. It can be seen that the aerodynamic
coefficients obtained by CFD qualitatively agree
with those obtained by EFD. In the experiments,
there are differences in
C
L
and C
M
in the process of
decreasing
AoA, compared with the data when the
process is increasing. Therefore, hysteresis occurs in
C
L
and C
M
in the experiments. On the other hand,
CFD could not detect the hysteresis in
C
L
and C
M
so
far, though it could detect the effect of the stall.
0
0.2
0.4
0.6
0.8
1
1.2
0 153045607590
EFD 0->90°
EFD 90->0°
CFD
C
D
AoA[°]
(a). The drag coefficient, C
D
.
0
0.2
0.4
0.6
0.8
1
1.2
0 153045607590
EFD 0->90°
EFD 90->0°
CFD
C
L
AoA[°]
(b). The lift coefficient, C
L
.
-0.2
0
0.2
0.4
0 153045607590
EFD 0->90°
EFD 90->0°
CFD
C
M
AoA[°]
(c). The pitching moment coefficient, C
M
.
Figure 4: AoA dependence of aerodynamic forces.
3.3 Estimating Aerodynamic
Coefficients
Aerodynamic forces were calculated by CFD for 247
cases, in which
AoA and the size (D
FCA
, R
MR
, THK
and w
) in Figure 5 were changed. The size was
varied in the design regulations for the discus, and
AoA was varied from 0° to 90°. In order to estimate
aerodynamic forces with respect to an arbitrary set
of values (
D
FCA
, R
MR
, THK and w), the concept of
‘inverse distance weighting interpolation’ was
applied. Inverse distance weighted interpolation are
ConcurrentOptimizationofFlightDistanceandRobustnessofEquipmentandSkillsinDiscusThrowing
201
based on the assumption that the interpolating
surface should be influenced most by the nearby
points and less by the more distant points. There are
four procedures. At first, each variable in the
arbitrary set and in all of the 247 cases were
normalized, respectively. The second procedure is to
calculate the Euclidean distance between the
normalized arbitrary set and each of 247 the
normalized cases. The third procedure is to find the
shortest Euclidean distance, l
i
, and the second
shortest Euclidean distance, l
j
. The forth procedure is
to estimate the aerodynamic forces from the known
CFD results on the basis of l
i
and l
j
. Defining the
subscript i as the shortest Euclidean distance and the
subscript j as the second shortest Euclidean distance,
the drag coefficient, C
D
, can be estimated from the
247 known CFD results in Equation (16). The lift
coefficient, C
L
, and the pitching moment coefficient,
C
M
, can be estimated in the same manner.
jjjMRjFCADi
iiiMRiFCADj
ji
MRFCAD
wTHKRDCl
wTHKRDCl
ll
wTHKRDC
,,,
,,,
1
,,,
,,
,,
(16)
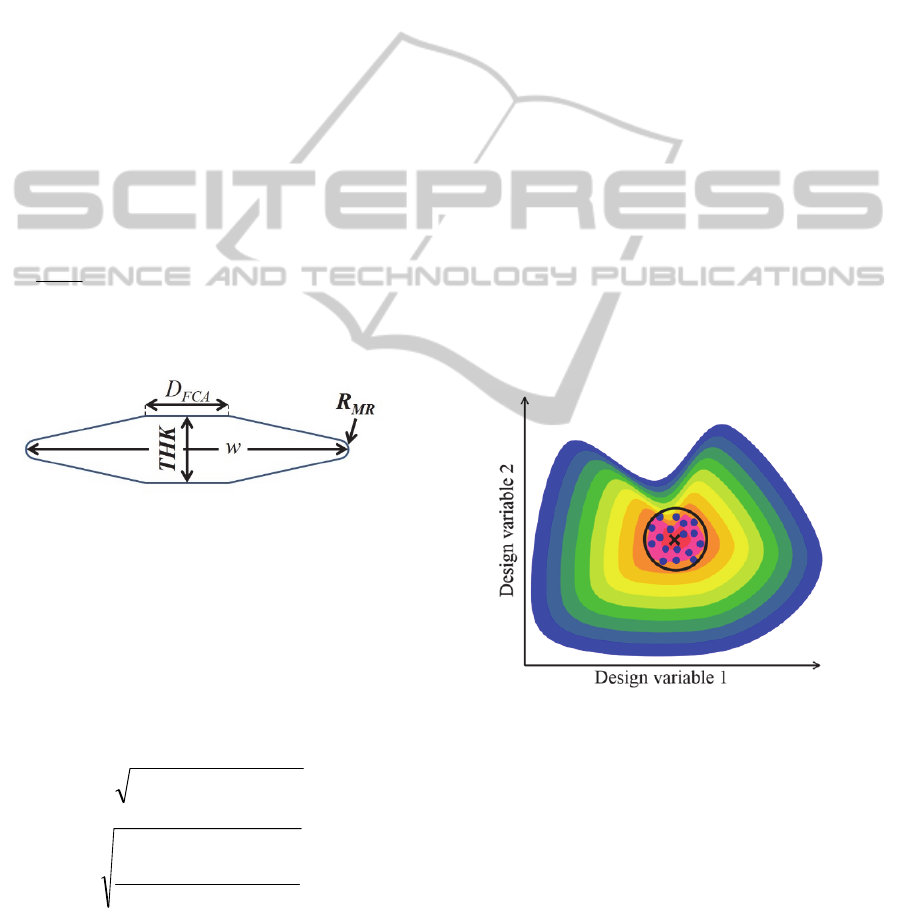
Figure 5: Design variables concerned with the size of the
discus.
4 OPTIMIZATION
4.1 Objective Function
The flight distance, which is considered to be the
first objective function, is defined as in Equation
(17).
22
1
fEfE
tYtXF
(17)
1
2
1
2
n
FDFD
F
n
i
candidatei
(18)
The flight time is denoted by t
f
. In the
optimization process, F1 should be minimized
because of the negative sign on the right hand side.
On the other hand, robustness is considered as
the second objective function. Robustness is defined
as the insensitivity to deviations from the local
optimal release and equipment conditions at the
local longest flight distance. In this study, the
standard deviation around the local optimal solution
is considered to be the second objective function,
which is defined in Equation (18). The concept of
robustness is explained by Figure 6, which shows a
contour map of the flight distance with respect to
two arbitrary design variables. The local longest
flight distance, ×, is denoted by FD
candidate
in
Equation (18). Here, FD stands for the flight
distance. The points denote the flight distances, FD
i
,
around FD
candidate
. The circle shows the range of
design variables corresponding with the human error
or the manufacturing error. Therefore, estimating F2
requires many trajectory simulations around
FD
candidate
. The number of trajectory simulations
with respect to sets of initial conditions around
FD
candidate
is denoted by n in Equation (18).
In the optimization process, both objective
functions should be minimized. The optimization is
carried out with the aid of an adaptive range genetic
algorithm (Sasaki et al. (2005)). The population for
each generation is 500, and the number of
generations is also set to 700.
Figure 6: The concept of ‘robustness’. Contour map of the
flight distance with respect to two arbitrary design
variables. The local longest flight distance is denoted by ×.
The points, ●, denote the flight distances around ×. The
circle shows the range of design variables corresponding
with the human error or the manufacturing error. The
standard deviation of ● is defined as robustness.
4.2 Design Variables
The fourteen design variables are shown in Table 1.
The ‘ranges for GA’, which are also shown in Table
1, are defined such that they can cover practical
values for the skill level of the thrower (Leigh et al.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
202

(2010)) and the design regulations for the discus.
Eight of the variables, from
γ to R in Table 1, are
concerned with the skill of the thrower at the point
of launch. The other six, from
I
T
to w, are concerned
with the equipment, which are controlled by the
designer. In this study, concurrent optimization of
both the thrower’s skill and the equipment is carried
out. Since the linear relationship between
I
L
(Moment of inertia on the longitudinal axis) and
I
T
is
derived from CAD data, I
L
can be uniquely
determined in accordance with I
T
.
Table 1: Design variables.
Design
variables
Abb. Ranges for
GA
Ranges
for MC
Flight path
angle
γ
15~60°
±5°
Azimuth
angle
Χ -30~30° ±5°
Roll angle Ψ -45~45° ±5°
Pitch angle Θ -60~60° ±5°
Yaw angle Φ -45~45° ±5°
Spin rate
about the x
b
axis
P -3~3 rev/s ±0.1
rev/s
Spin rate
about the y
b
axis
Q -3~3 rev/s ±0.1
rev/s
Spin rate
about the z
b
axis
R 0~7rev/s ±0.1
rev/s
Moment of
inertia on the
transverse axis
I
T
0.0055~0.006
kgm
2
±0.0001
kgm
2
Mass m
D
1.005~1.025
kg
±5 g
Diameter of the
flat center area
D
FCA
50~57 mm
±0.1 mm
Radius of the
metal rim
R
MR
5.85~6.45
mm
±0.1 mm
Thickness THK
37~39 mm
±0.1 mm
Width W
180~182 mm
±0.1 mm
Since a right-handed thrower is assumed, the
launch position is considered to be in the right-hand
side of the throwing circle. The launch position is
assumed to be (
X
E
, Y
E
, Z
E
) = (1.0, 1.0, −1.6) in this
study. The negative sign of Z
E
means the vertically
upward direction, and the value of -1.6 is almost the
highest launch position achievable for women. The
release height is generally 90% of the thrower’s
height. The magnitude of the velocity vector at
launch is assumed to be 26 ms
-1
.
4.3 Constraint
A constraint, g
1
, is considered, as shown in Equation
(19). This constraint means that the discus should
make ground contact within the sector.
0
1
fEfELine
tYtXYg
(19)
fEfELine
tXtXY
2
92.34
tan
(20)
Here,
Y
Line
(X
E
(t
f
)) is the side line value of Y
E
corresponding to X
E
(t
f
), which is defined by
Equation (20). The angle of 34.92° is shown in
Figure 1.
4.4 Monte Carlo Method
In order to estimate F2 in Equation (18), the flight
distance should be simulated around FD
candidate
. The
higher the value of
n in Equation (18), the more
convergent (constant) F2 will be, but the simulations
will take a longer time to complete. It is possible to
simulate
FD
i
with respect to a constant interval for
each control and design variable. However, fourteen
design variables are too many to do this. Therefore,
the Monte Carlo method was applied. Monte Carlo
methods rely on repeated random sampling to obtain
numerical results. The simulation points are defined
by the uniform random numbers in this study. The
number of simulations (time for the simulation) can
be controlled easily by changing
n in Equation (18).
0
1
2
3
12345678910
n=50
n=10,000
F2
Trial number
Figure 7: The n dependence of F2. In the case of n=50, the
standard deviation among the ten trials is 0.29 meters. In
the case of n=10,000, the standard deviation is 0.025
meters.
Figure 7 shows the dependence on n of F2. Ten
trials (abscissa in Figure 7) were carried out, when
the flight distance of the candidate for the optimal
ConcurrentOptimizationofFlightDistanceandRobustnessofEquipmentandSkillsinDiscusThrowing
203

solution, FD
candidate
, was 78 meters. It can be seen
that the value of F2 is almost constant among all of
the trials in the case of
n=10,000, while it is not
constant in the case of n=50. In the case of n=50, the
standard deviation among the ten trials is 0.29
meters. In this study,
n=50 is applied to minimize
the simulation time on the computer, although there
is then an uncertainty of 0.29 meters (there is a
possibility of an inaccuracy of 0.29 meters in
F2
because of the smaller number of trajectory
simulations
n, which depends on the random
number.).
The range for each design variable should be
comparable with the human error in the competition
and manufacturing error. Here, the ranges of the
design variables are shown as ’Range for MC’ in
Table 1.
5 RESULTS AND DISCUSSIONS
The trade-off between F1 and F2 is shown in Figure
8. Although the lowest value (longest flight distance
and smallest standard deviation) is ideal for each of
the two objective functions, it is impossible for two
objective functions to achieve their lowest values
simultaneously. This is because the two objective
functions conflict with each another. Therefore,
multi-objective optimization involves a set of
solutions, each of which is better regarding one
objective function but worse regarding the others.
These kinds of objective-conflicting solutions are
called Pareto-optimal solutions, and represent the
trade-off features among the objective functions. If
F1 were a single objective (not optimized regarding
F2), it would be possible to achieve a flight distance
of 79.0 meters, which is 2 meters longer than the
world record. However, it is not robust. There is a
possibility of losing flight distance of 1.3 meters
(=standard deviation), if the release condition
slightly deviates from the optimal release condition.
If
F2 were a single objective (not optimized
regarding F1), the flight would be robust for the
deviation from the optimal release condition.
However, the flight distance is merely 45.3 meters.
The sweet spot, where both objective functions have
better values simultaneously, is denoted by × in
Figure 8. The flight distance is 78.8 meters at the
sweet spot, while the standard deviation is 0.48
meters. Both the objective functions and the design
variables are also shown in Table 2. The spin rate
about the transverse axis is a relatively high
R of
6.22 rev/s, the moment of inertia on the transverse
axis is a relatively high
I
T
of 0.0058 kgm
2
and the
mass is almost the lowest permissible
m
d
of 1.007
kg.
The lift coefficients,
C
L
, as a function of AoA are
shown in Figure 9. The open circles denote CFD
results for the minimum case, in which all variables
concerned with the sizes are the lowest. The open
triangles denote CFD results in the maximum case,
in which all variables are the highest. The closed
triangles denote CFD results in the case of the sweet
spot solution. It can be seen that the sweet spot
solution is close to other cases, except around the
stalling angle. Stalling for the sweet spot solution
occurs at 34°, while stalling for other cases occurs at
less than 29°.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-80 -75 -70 -65 -60 -55 -50 -45
F2 [m]
F1 [m]
Figure 8: Trade-off (Pareto front) between both objective
functions. An × denotes the sweet spot solution.
Table 2: Sweet spot solution.
Abb. Sweet spot solution
F1 -78.82 m
F2 0.72 m
γ
37.70°
χ 11.07°
Ψ 1.78°
Θ 34.30°
Φ 36.29°
P 0.024 rev/s
Q 0.018 rev/s
R 6.22 rev/s
I
T
0.0058 kgm
2
m
D
1.007 kg
D
F
CA
55.09 mm
R
M
R
6.31 mm
THK
38.01 mm
w
181.51 mm
Figure 10 shows pressure distribution for three
cases shown in Figure 9. The wind direction is from
the left to the right. The wind speed was set at 30
ms
-1
, and the angle of attack was set to 30°. The
highest gauge pressure of 600 Pa is denoted by the
red, while the lowest gauge pressure of -2000 Pa is
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
204
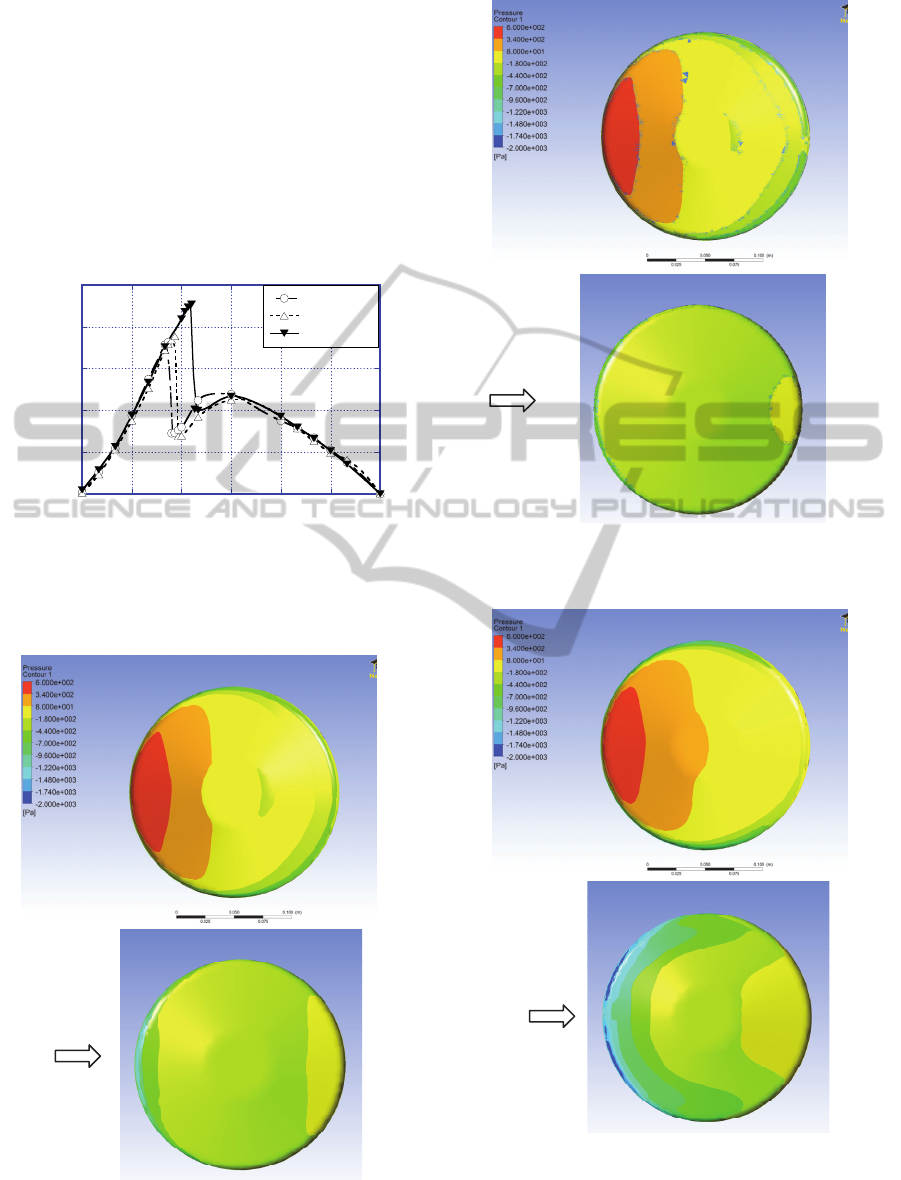
denoted by the blue. It can be seen that the pressure
difference between the pressure side and the suction
side becomes a maximum for the sweet spot solution
(Figure 10-c). This means that the lift for the sweet
spot solution becomes the highest of these three
cases. The high pressure appears on the upstream
side of the pressure side in all three cases. This is
because the effective angle of attack on the upstream
side becomes larger than that on the downstream
side. The angle of incline for the sweet spot solution
is 16.72°.
0
0.2
0.4
0.6
0.8
1
0 153045607590
Min
Max
Sweet spot
C
L
AoA [°]
Figure 9: AoA dependence of C
L
.
Min: (D
FCA
, R
MR
, THK, w)= (50, 5.85, 37, 180)
Max: (D
FCA
, R
MR
, THK, w)= (57, 6.45, 39, 182)
Sweet spot: (D
FCA
, R
MR
, THK, w)= (55, 6.3, 38, 181.5)
10-a) Maximum case. The upper is the pressure side,
while the lower is the suction side.
(D
F
CA
, R
M
R
, THK, w)= (57, 6.45, 39, 182)
10-b) Minimum case. The upper is the pressure side, while
the lower is the suction side.
(D
FCA
, R
MR
, THK, w)= (50, 5.85, 37, 180)
10-c) Sweet spot solution. The upper is the pressure side,
while the lower is the suction side.
(D
F
CA
, R
M
R
, THK, w)= (55, 6.3, 38, 181.5)
Figure 10: Pressure distribution at AoA=30° and 30ms-1.
Win
d
Win
d
Win
d
ConcurrentOptimizationofFlightDistanceandRobustnessofEquipmentandSkillsinDiscusThrowing
205

6 CONCLUSIONS
In this study, two objective functions are considered.
One is the flight distance, the other is the robustness.
The flight distance is the most important, but
robustness is also important, especially for the world
of competitive sports. Therefore, concurrent
optimization of flight distance and robustness of
discus throwing is carried out using a genetic
algorithm. Fourteen design variables are considered,
which include the skill of the thrower and the
inherent features of the equipment. The design
variables concerned with the skill and the equipment
were treated concurrently. The conclusions are
summarized as follows:
There is a trade-off between flight distance and
robustness.
The longest flight distance that could be
achieved was 79.0 meters. However, it is not
robust. There is a possibility of losing flight
distance of 1.3 meters, if the release condition
slightly deviates from the optimal release
condition.
The flight distance is 78.8 meters at the sweet
spot solution, where both objective functions of
the flight distance and the robustness have
better values simultaneously. There is a
possibility of losing flight distance of 0.48
meters.
The stalling angle for the sweet spot solution is
relatively high. In other words, the maximum
lift for the sweet spot solution becomes greater.
At the sweet spot solution, the spin rate about
the transverse axis is a relatively high
R of 6.22
rev/s, the moment of inertia on the transverse
axis is a relatively high
I
T
of 0.0058 kgm
2
and
the mass is almost the lowest permissible
m
d
of
1.007 kg. The width is a relatively high
w of
181.5mm, the thickness is 38mm, the metal rim
radius is a relatively high
R
MR
of 6.3mm and
the diameter of the flat center area is a
relatively high
D
FCA
of 55mm.
ACKNOWLEDGEMENTS
This work is supported by a Grant-in-Aid for
Scientific Research (A), Japan Society for the
Promotion of Science.
REFERENCES
Deb, K., 2001. Multi-Objective Optimization using
Evolutionary Algorithms. Wiley, New York
Hubbard, M. and Cheng, K., 2007. Optimal discus
trajectories, J Biomechanics, 40, pp.3650-3659.
Leigh, S., Liu, H., Hubbard, M. and Yu, B., 2010.
Individualized optimal release angles in discuss
throwing, J Biomechanics, 43, pp.540-545.
Sasaki, D., and Obayashi, S., Efficient search for trade-
offs by adaptive range multi-objective genetic
algorithms, AIAA Journal of Aerospace Computing,
Information, and Communication, 2005, pp.44-64.
Seo, K., Kobayashi, O., Murakami, M., Yorita, D., Nagai,
H. and Asai, K., 2010. Simulation of the trajectory of a
punted rugby ball taking into account the
asymmetrical pressure distribution caused by the
seams. Journal of Visualization, 13, pp. 97-105.
Seo K., Shimoyama K., Ohta K., Ohgi Y. and Kimura Y.,
2012. Aerodynamic behaviour of a discus, Procedia
Engineering 34, pp.92-97.
Stevens, B. and Lewis, F., 2003. Aircraft control and
simulation, Wiley. Hoboken, New Jersey, 2
nd
edition.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
206
