Enriching Traditional Databases with Fuzzy Deﬁnitions to Allow Flexible

and Expressive Searches

Victor Pablos-Ceruelo and Susana Munoz-Hernandez

Facultad de Inform

atica, Universidad Polit

ecnica de Madrid, Campus de Montegancedo s/n, Boadilla, Spain

Keywords:

Databases, Fuzzy Logic, Search Engine.

Abstract:

Although the relevance of fuzzy information to represent concepts of real life is evident, almost all databases

contain just crisp information. The main reason for this, apart from the tradition, is that fuzzy information

is most of the times subjective and storing all users points of view is unfeasible. Allowing fuzzy concepts in

the queries increases the queries’ expressiveness and asking for cheap products, big size, close hotels, etc is

much more interesting that asking for products with a price under X, of the size Y, hotels at most X kilometers

far, etc. The way we propose for achieving this more expressive databases’ queries is adding to the basic

knowledge offered by a database (e.g. distance to hotel is 5 km) the link between this crisp concept and

multiple fuzzy concepts that we use in real life (e.g. close hotel). We present FleSe, a framework for searching

databases in a ﬂexible way, thanks to the fuzzy concepts that we can deﬁne. In this paper we describe the easy

procedure that let us deﬁne fuzzy concepts and link them to crisp database ﬁelds.

1 INTRODUCTION

Databases are, in principle, for storing crisp data, not

fuzzy data. So, we cannot ask which are the restau-

rants close to our place, but which ones are at most

2km far from our place. Adding a column of text type

and storing inside the value “close” could be a solu-

tion for examples like this one, but it does not work

always because of the inherent subjective character of

fuzzy attributes. Take, for example, Andrew’s height:

1’90 cm. There is no problem in storing this crisp

value (it is just a ﬂoat number), but it is no so easy if

we try to store if Andrew is “tall”, “very tall”, “no tall

at all” or any other fuzzy value, because it might not

be true for all the people retrieving the value from the

database. Elsa, whose height is 1’41 cm, might con-

sider him very tall, while Luzia, whose height is 1’72,

might consider him just tall.

Our proposal to allow querying the database with

fuzzy concepts relies on knowing the link between

any of them and the non-fuzzy concept stored in the

database. This link is what we (humans) use to de-

termine how much the fuzzy concept is satisﬁed. We

present here a framework for encoding this relations,

always with the subjective characteristic of fuzzy con-

cepts in mind. The main difference with respect to

other approaches is that we do not provide a complex

syntax for querying the database nor a free text area

ﬁeld to enter the query. We evaluate the information

in the conﬁguration ﬁle and in the database to deter-

mine all the possible queries that a user can perform

and provide a form to enter any of this queries.

The paper is structured as follows: In preliminar-

ies (Sec. 2) we introduce to the ideas our framework

is based on. In implementation details (Sec. 3) we

talk about the underlying infrastructure needed for the

framework to work as expected. We explain just after

how to use the framework from a developer point of

view (Sec. 4) and the search engine a general user can

use to ask queries (Sec. 5). Conclusions and current

work go in last place (Sec. 6), as usual.

2 PRELIMINARIES

It was Lotﬁ Zadeh in 1965 who introduced fuzzy set

theory (Zadeh, 1965), proposed their division in type-

1 and type-2 fuzzy sets and systems (Zadeh, 1975)

and justiﬁed its existence in his paper ”Is there a need

for fuzzy logic?” (Zadeh, 2008).

In this section we talk a little bit about history, fo-

cusing in what matters for our contribution: Fuzzy

Queries to Regular Databases (Subsec. 2.1), and Pri-

orities in Fuzzy Logic (Subsec. 2.2).

111

Pablos-Ceruelo V. and Muñoz Hernández S..

Enriching Traditional Databases with Fuzzy Deﬁnitions to Allow Flexible and Expressive Searches.

DOI: 10.5220/0005074101110118

In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 111-118

ISBN: 978-989-758-053-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2.1 Fuzzy Queries to Regular Databases

Getting fuzzy answers for fuzzy queries from non-

fuzzy information stored in non-fuzzy databases has

been studied in some works, as SQLF, presented by P.

Bosc and O. Pivert in (Bosc and Pivert, 1995), FQL,

presented by Takahashi (Takahashi, 1991), FIIS, pre-

sented by M. Zemankova (Zemankova, 1989), FIRST,

presented by D. Lucarella and R. Morara (Lucarella

and Morara, 1991), the tool proposed by Chen and

Jong (Chen and Jong, 1997) and others. Very

good revisions of this ones and some other propos-

als are the works of Leonid Tineo (Tineo, 2005) and

Herrera-Viedma and L

opez-Herrera (Herrera-Viedma

and L

opez-Herrera, 2010).

Most of the works mentioned before focus in im-

proving the efﬁciency of the existing procedures, in

including new syntactic constructions, in allowing to

introduce in the queries the conversion between the

non-fuzzy values needed to execute the query and the

fuzzy values in the query, or in improving the trans-

lation of the fuzzy query into the SQL syntax (so any

regular database can answer it). Our proposal focus

less on the technical aspects (so we cannot compare

the evaluation speed or the resources consumption of

ours against any of them) because it tries to present

the user an interface intelligent enough to allow the

user to pose only the queries that we can answer from

the knowledge introduced in the conﬁguration ﬁle and

the information in the database. It is, the framework

is able to determine the whole set of queries that it can

answer from the knowledge introduced in the conﬁg-

uration ﬁle and presents the user a web interface to

pose easily any of this queries.

Our work is maybe more similar to works re-

lated to information retrieval, like the one of Ropero,

omez, Carrasco and Le

on (Ropero et al., 2012)

or the one of Zadrozny and Nowacka (Zadrony and

Nowacka, 2009), although we consider it rather dif-

ferent. Most of the works in this line focus in creating

an index for answering queries by using different term

weighting procedures (even logic-based ones). Their

goal is obtaining an index with enough information to

answer any query, some of them analyzing it previ-

ously by using natural language processing and some

others by providing a slightly complicated query syn-

tax. Ours, as told before, focus in providing an easy

to use interface allowing the user to represent with it

any query that can be answered from the knowledge

introduced in the conﬁguration ﬁle.

When starting the development of our proposal

we wanted to do it under the logic programming

paradigm, because we know that it is more declara-

tive

than the other ones. The frameworks for fuzzy

logic allowing the developer to code programs un-

der the logic programming paradigm (called fuzzy

logic systems) we know about are Flopper (Morcillo

and Moreno, 2008), Fuzzy Prolog (Guadarrama et al.,

2004), Rfuzzy (Mu

noz-Hern

andez et al., 2011) and

FuzzyDL (Bobillo and Straccia, 2008).

2.2 Priorities in Fuzzy Logic

The inherent subjective character of fuzzy concepts

needs to be taken into account when performing fuzzy

searches. Some users might want to redeﬁne or per-

sonalize some concepts, but some others might not

want to. So, we might give more priority to the con-

cepts redeﬁned by users, but only when they are the

ones posing the query.

In (Mu

noz-Hern

andez et al., 2011) the authors

extend the multi-adjoint satisfaction and immediate

consequences operator in (Medina et al., 2004; Med-

ina Moreno and Ojeda-Aciego, 2002) to take care

of conditions and introduce a three levels priority

system. These three levels were designed to dis-

tinguish results computed by rules that do not rely

on other rules (highest priority), rules that rely on

others (medium priority) and rules used when no

other rule was able to obtain a valid result (low-

est priority). The proposal was adequate but, as

the same authors pointed out in (Pablos-Ceruelo

and Mu

noz-Hern

andez, 2011), insufﬁcient for mod-

elling user preferences. This is why in (Pablos-

Ceruelo and Mu

noz-Hern

andez, 2011) they changed

the three symbols by a real number between 0

and 1, in the direction proposed by the authors of

(Theodorakopoulos and Baras, 2004). We take the

idea of using priorities to represent user preferences

from (Pablos-Ceruelo and Mu

noz-Hern

andez, 2011;

Theodorakopoulos and Baras, 2004).

3 IMPLEMENTATION DETAILS

The framework we present runs on a computer with a

Linux Operating System and is divided in two appli-

cations: the ﬁrst one written in Java and running on

a Tomcat server and the other one written in Prolog

(Lloyd, 1987; O’Keefe, 1990; Sterling and Shapiro,

1987) and executed by demand of the ﬁrst one. The

We say that it is more declarative because we know that

it is not fully declarative yet. It removes the necessity to

specify the ﬂow control in most cases, but the programmer

still needs to know if the interpreter or compiler implements

depth or breadth-ﬁrst search strategy and left-to-right or any

other literal selection rule.

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

112

database is managed directly by the Prolog code,

which allows us to use the Prolog facilities for linking

to it: we are not restricted to any database or database

interface.

The justiﬁcation of using Prolog lies on the fact

that it is one of the most successful programming lan-

guages for representing knowledge in computer sci-

ence. Its main advantage with respect to the other

ones is being a more declarative programming lan-

guage. Prolog is based on logic. It is usual to identify

logic with bi-valued logic and assume that the only

available values are “yes” and “no” (or “true” and

“false”), but logic is much more than bi-valued logic.

In fact we use fuzzy logic (FL), a subset of logic that

allow us to represent not only if an individual belongs

or not to a set, but the grade in which it belongs. Sup-

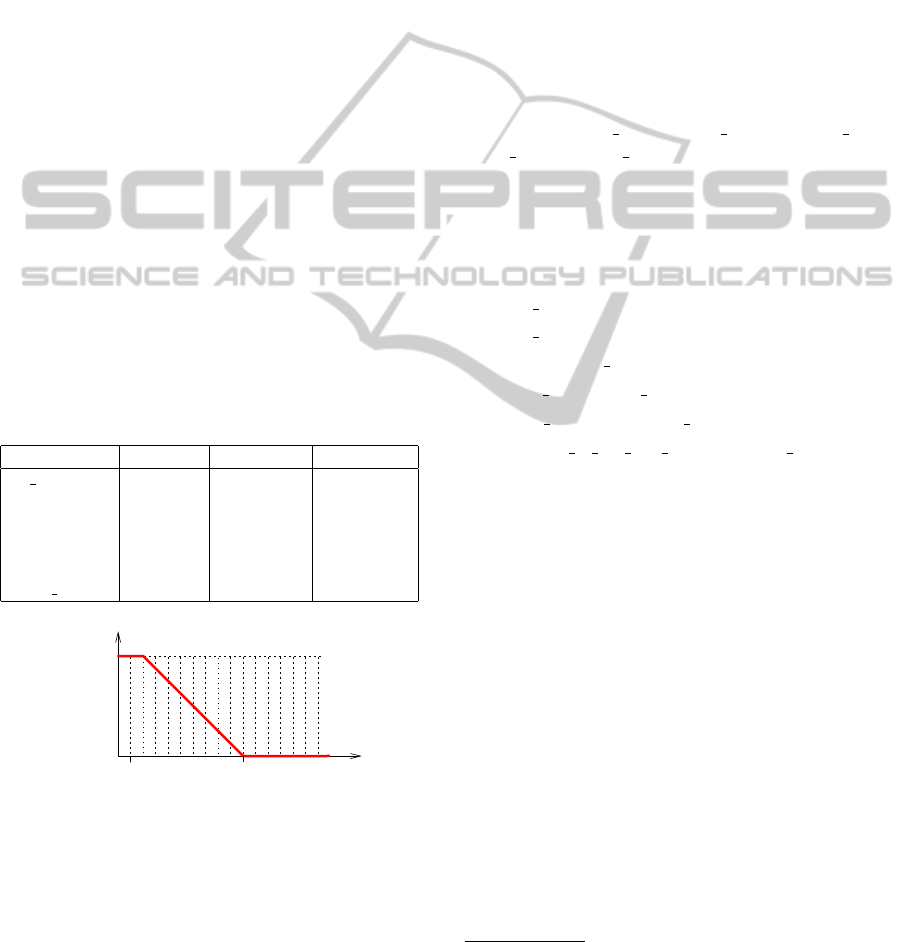
posing the database contents in Table. 1, the deﬁnition

for “close” in Fig. 1 and the question “Is restaurant X

close to the center?” with FL we can deduce that Il

tempietto is “deﬁnitely” close to the center, Tapasbar

is “almost” close, Ni Hao is “hardly” close and Kenzo

is “not” close to the center. We highlight the words

“deﬁnitely”, “almost”, “hardly” and “not” because the

usual answers for the query are “1”, “0.9”, “0.1” and

“0” for the individuals Il tempietto, Tapasbar, Ni Hao

and Kenzo and the humanization of the crisp values is

done in a subsequent step by defuzziﬁcation.

Table 1: Restaurants’ database contents.

name distance price avg. food type

Il tempietto 100 30 italian

Tapasbar 300 20 spanish

Ni Hao 900 10 chinese

Kenzo 1200 40 japanese

Zalacain 2000

Don Jamon spanish

100 1000 distance

Figure 1: Close fuzziﬁcation function.

Choosing Java instead of other programming lan-

guages is a decision guided by the necessity to have

a good communication between Prolog and the user

interface. Since we decided to have a web user in-

terface and use Asynchronous Ajax for improving the

user experience, and Java has very well management

of asynchronous http petitions and libraries to control

Prolog, the decision was easy.

4 THE FRAMEWORK

We present here how to deﬁne the links between the

fuzzy concepts and the ﬁelds in the database. Since

Prolog offers us to access the database as if a predicate

it was, we take this as a fact and start by the deﬁnition

needed by the framework to understand what is stored

in each database column.

The construction in Eq. 1 serves to deﬁne what

is stored in each database column. In the con-

struction pT is the name of the database table

or virtual database table (vdbt)

, pA is the arity

of the vdbt, pN is the name assigned to a col-

umn of the vdbt pT and pT

is the type of the

information stored in the column, (a basic type,

one of { boolean type, enum type, integer type,

f loat type, string type }). We provide an exam-

ple in Eq. 2 to clarify. In the example we deﬁne the

restaurant database with four columns. The ﬁrst for its

name, the second for the food type served there, the

third for the restaurant’s price average and the last one

for the distance to the city center from that restaurant.

de f ine database(pT/pA,[(pN, pT

)]) (1)

de f ine database( restaurant/4,

(name, string type),

( f ood type, enum type),

(price average, integer type),

(distance to the city center, integer type)]). (2)

The previous construction (Eq. 1) serves too to de-

ﬁne the non-fuzzy predicates we can use when linking

fuzzy and non-fuzzy concepts. In addition to the links

we can deﬁne truth values for some fuzzy predicates

and under some conditions. The construction in Eq. 3

serves to deﬁne the rare situation in which for all the

individuals in the vdbt we have the same result. It is

usually limited to some individuals by using the con-

structions in Eqs. 4, 5 and 6 as tails (explained below).

In Eq. 3 the variable pT means the same as in Eq. 1,

TV is the truth value (a ﬂoat number between 0 and

1) and f PredName is name of the fuzzy predicate we

are deﬁning. In Eq. 7 we present an example in which

we say that all the restaurants are cheap with a truth

value of 0.5.

We usually name the database “virtual database table”

(vdbt) because the database that we deﬁne can be mapped

to more than one database by using Prolog to database li-

braries. We do not enter here into these low-level details.

EnrichingTraditionalDatabaseswithFuzzyDefinitionstoAllowFlexibleandExpressiveSearches

113

f PredName(pT ) :∼ value(TV) (3)

i f ( pN(pT) comp value). (4)

with credibility(credOp, credVal) (5)

only f or user

UserName

(6)

cheap(restaurant) :∼ value(0.5) (7)

The constructions in Eqs. 4, 5 and 6 serve as tails

for the constructions in Eqs. 3, 11, 13, 16, 17, 19, 20

and 23. The tail in Eq. 4 (not applicable to the

construction in Eq. 23) serves to limit the in-

dividuals for which we want to use the fuzzy

clause or rule (limits its application to subsets

of the set of individuals in the vdbt). In the

construction pN and pT mean the same as in

Eq. 1, comp can take the values “is equal to”,

“is di f f erent f rom”, “is bigger than”,

“is lower than”, “is bigger than or equal to” and

”is lower than or equal to” and value can be of

type integer type, enum type or string type. The

only restrictions are that the type of value must be

the same as the one given to to the column pN of pT

and that if they are of type enum type or string type

the only available values for comp are “is equal to”

and “is di f f erent f rom”. We show an example in

Eq. 8 in which we say that the restaurant Zalacain is

cheap with a truth value of 0.1.

cheap(restaurant) :∼ value(0.1)

i f (name(restaurant) is equal to zalacain). (8)

The tail in Eq. 5 serves to deﬁne a credibility for a

clause, together with the operator needed to combine

it with its truth value. In its syntactic deﬁnition in

Eq. 5 credVal is the credibility, a number of ﬂoat type,

and credOp is the credibility operator.

We show an

example in Eq. 9 in which we say that the restaurant

Don Jamon is cheap with a truth value of 0.3 but this

rule has a credibility of 0.8 and the operator that must

be used to combine the credibility with the truth value

is the minimum (called too G

odel conjunctor).

cheap(restaurant) :∼ value(0.3)

i f (name(restaurant) is equal to don jamon)

with credibility(min, 0.8). (9)

The tail in Eq. 6 is aimed at deﬁning personalized

rules, rules that only apply when the user logged in

and the user in the rule are the same one. In the con-

struction Username is the name of any user, a string.

The credibility operator (called conjunctor in most of

the papers cited in Sec. 1) is a mathematical functions that

must be monotone and non-decreasing in their coordinates.

Immediate examples for conjunctors that come to mind are

product, Łukasiewicz conjunctor and G

odel conjunctor. All

of them are included in the framework. They can be used

by writting “prod”, “luka” and “min” in the ﬁeld “credOp”.

We show an example in Eq. 10 in which we say that

Lara considers that the restaurant Zalacain is not close

to the center. So, if it is she who poses a query to the

system asking for restaurants close to the city center

she will obtain that the Zalacain restaurant is not.

close to the city center(restaurant) :∼ value(0)

i f (name(restaurant) is equal to zalacain)

only f or user

Lara

(10)

The links between non-fuzzy values the individ-

uals in the database have and the fuzzy concepts is

done by means of the constructions called fuzziﬁca-

tions, of the form shown in Eq. 11. This fuzziﬁca-

tion functions allow us to know how much satisﬁed

is a fuzzy predicate for some individual stored in our

database, from a non-fuzzy value that we have in the

database for that individual. In Eq. 11 pN and pT

mean the same as in Eq. 1, f PredName is the name

of the fuzzy predicate that we are deﬁning (the fuzzi-

ﬁcation), [(valIn, valOut)] is a list of pairs of values

such that valIn belongs to the domain of the fuzziﬁ-

cation function and valOut to its image

. An example

in which we compute how cheap is a restaurant from

its average price is presented in Eq. 12. The graphi-

cal representation corresponding to this example is in

Fig. 2.

f PredName(pT ) :∼ f unction( pN( pT ),

[ (valIn, valOut) ]). (11)

cheap(restaurant) :∼ f unction(

price average(restaurant),

[(0, 1),(10, 1),(20, 0.9),(50, 0), (200,0)]). (12)

cheap

10 100 euros

Figure 2: Cheap function (for restaurant).

When deﬁning the satisﬁability of a fuzzy pred-

icate from a value stored in a database we can get

an unexpected behaviour if the database contains a

null value. To avoid this malfunctioning of the sys-

tem we provide syntax for deﬁning the satisfaction of

the fuzzy concepts in this cases. We usually say that

this constructions (shown in Eq. 13) are for deﬁning

default truth values for the fuzzy concepts. In Eq. 13

pT means the same as in Eq. 1, f PredName the same

[(valIn,valOut)] is basically a piecewise function deﬁ-

nition, where each two contiguous points represent a piece.

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

114

as in Eq. 11 and TV the same as in Eq. 3. We provide

two examples in Eqs. 14 and 15 in which we say that,

in absence of information, we consider that a restau-

rant will not be close to the city center (this is what the

zero value means) and that, in absence of information,

a restaurant is considered to be medium cheap

f PredName(pT ) :∼ de f aults to(TV ) (13)

close to the city center(restaurant)

:∼ de f aults to(0). (14)

cheap(restaurant) :∼ de f aults to(0.5). (15)

In addition to the deﬁnition of fuzzy concepts

from non-fuzzy concepts, the deﬁnition of their sat-

isfaction in special cases and the deﬁnition of default

values to avoid that the inference process stops when

a needed value is missing, we can deﬁne fuzzy con-

cepts from other fuzzy concepts. The possibility to do

this allows us to increase the number of fuzzy predi-

cates that can be used to query the database. We can

do that by using rules, synonyms and antonyms.

Rules allow us to deﬁne the satisfaction of a fuzzy

predicate from the satisfaction of other fuzzy pred-

icates. We have two syntactical forms for deﬁning

rules, the ﬁrst one used when the body depends on

more than one fuzzy predicate, shown in Eq. 16, and

the second one when it depends in just one, shown

in Eq. 17. In Eq. 16 aggr is the aggregator used to

combine the truth values of the fuzzy predicates in

complexBody, which is just a conjunction of names

of fuzzy predicates (and the vdbt they are associated

to, represented by pT ), while in Eq. 17 simplexBody

is just the name of a fuzzy predicate (and the vbdt it

is associated to). In both of them pT means the same

as in Eq. 1 and f PredName the same as in Eq. 11.

We show an example in Eq. 18 in which we say that

a restaurant is a tempting restaurant depending on the

worst value it has between being close to the center

and being cheap, which means that a restaurant must

be close to the center and cheap at the same time to

consider it a tempting restaurant.

f PredName(pT ) :∼ rule(aggr, complexBody) (16)

f PredName(pT ) :∼ rule(simpleBody) (17)

tempting restaurant(restaurant) :∼ rule( min,

( close to the city center(restaurant),

cheap(restaurant) )) (18)

The syntax for deﬁning a fuzzy predicate from a

synonym is shown in Eq. 19 and the one for deﬁn-

ing it from an antonym in Eq. 20. In Eqs. 19 and 20

We include two examples here so if one builds a pro-

gram by taking all the examples in the contribution the rule

in Eq. 18 the framework is able to obtain results for all the

restaurants in our database.

pT means the same as in Eq. 1, credOp and credVal

the same as in Eq. 5 and f PredName the same as

in Eq. 11, while f PredName2 is the fuzzy predicate

from which we are deﬁning the synonym or antonym.

Its name must be different from f PredName. In the

examples in Eqs. 21 and 22 we deﬁne an unexpensive

restaurant as a cheap restaurant and an expensive one

as the opposite of a cheap one.

f PredName(pT ) :∼

synonym o f ( f PredName2(pT ),

crepOp, credVal ) (19)

f PredName(pT ) :∼

antonym o f ( f PredName2(pT ),

crepOp, credVal ) (20)

unexpensive(restaurant) :

synonym o f (cheap(restaurant), prod,1). (21)

expensive(restaurant) :

antonym o f (cheap(restaurant), prod,1). (22)

Apart from the deﬁnition of fuzzy concepts, we

might be interested in allowing the user to search for

individuals that have a characteristic similar to the

characteristic they enter in the query. Suppose we are

looking for a “Mediterranean” food restaurant and we

have in the database the values “Spanish”, “Italian”,

“Portuguese”, etc. We want to allow the user to ask

for restaurants serving food similar to the “Mediter-

ranean” one, so we need to tell the system about this

relation. This is what the construction in Eq.23 serves

for. In Eq. 23, pT and pT

mean the same as in Eq. 1,

TV the same as in Eq. 3 and value1 and value2 are

two values for the vdbt column pT

of the vdbt pT .

In the example in Eq. 24 we say that the food type

mediterranean is 0.6 similar to the spanish one (but

not in the other way. If we want to say that the span-

ish food is 0.6 similar to the mediterranean one we

need to add another line of code saying that).

similarity between(pT, pT

(value1), pT

(value2),

TV). (23)

similarity between( restaurant,

f ood type(mediterranean),

f ood type(spanish), 0.6). (24)

5 THE FRAMEWORK USER

INTERFACE

The framework user interface gets a lot of information

from the framework, providing the ﬁnal user an inter-

EnrichingTraditionalDatabaseswithFuzzyDefinitionstoAllowFlexibleandExpressiveSearches

115

face “intelligent” enough to allow him to perform any

query that the framework can solve with the knowl-

edge it has.

Suppose, for example, that we are looking for a

restaurant near the city center and with a menu price

under 25 e. We start choosing the database we want

to query, “db leisure” (Fig. 3).

Figure 3: Choosing the database.

Once selected the user interface allows us to select

what are we looking for (a restaurant this time, Fig. 4).

Figure 4: Choosing what we are looking for.

The interface shows then a combo for choosing a

fuzzy or non-fuzzy attribute of the individuals and a

plus sign to the right (Fig. 5). The attributes are the

names we give to the columns by using the construc-

tion in Eq. 1 and the fuzzy predicates deﬁned by using

the constructions in Eqs. 3, 11, 13, 16, 17, 19, 20 and

23 (although we can use multiple sentences to deﬁne

a fuzzy predicate it will appear only once). The plus

sign serves to add more conditions to the query (it

only has a line at the beginning) and the “show op-

tions” label can be used to switch the operator we use

to combine the truth values from minimum to product,

Łukasiewicz or any other (it needs to be previously

deﬁned in the framework).

One of the most interesting characteristics of the

framework user interface is that it interacts with the

framework, so it knows if the attribute selected is

fuzzy or not. In case the predicate is fuzzy it shows

to its left two combos, one for choosing negation and

the other one for choosing a modiﬁer (Fig. 6), while if

it is a non-fuzzy one it shows a combo for choosing a

comparison operator and, depending on the operator

chosen, a combo with the available values or a free

text ﬁeld for entering a value (Fig. 7). We show in

Fig. 8 the query we want to pose to the system.

After posing the query (Fig. 8), we need to press

the button labelled “search”. The search engine then

shows the query results, grouped in ﬁve tabs: “10 best

Figure 5: The available attribute(s) for writing the query.

Figure 6: Available modiﬁers for the fuzzy attribute.

Figure 7: Available comparison operators for the non-fuzzy

attribute.

Figure 8: Query example.

results”, “results over 70%”, “results over 50%”, “re-

sults over 0%” and “all results”. This allows the user

to select the results that best ﬁt his query or, if they do

not satisfy his expectations, to navigate through re-

sults that do not satisfy the query entered but might

be the ones he is looking for. We show in Fig. 9 the

results for the query entered in Fig. 8. The data in

the ﬁrst column corresponds to the information in the

virtual database table. The user can choose between

seeing it or not.

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

116

Figure 9: Answers returned for the query example in Fig. 8.

Figure 10: Selection of the fuzzy attribute the user wants to personalize and introduction of the user deﬁnition.

The button “Personalize Program File” allows the

user to introduce his point of view about a fuzzy con-

cept. In this way the user can personalize how the

framework translates the non-fuzzy attributes stored

in the database into the fuzzy ones he uses in his

query. When pressing the button the interface shows

a pop-up window (Fig.10) in which it asks the user

which fuzzy predicate he wants to personalize and his

preferences for the fuzziﬁcation of the values stored

in the database.

At last, but not least important that the previous

facilities, we allow any user to use our application for

querying any existing (and available) database. The

only requisite is that they need to upload their pro-

gram ﬁle to our application, for which they need to

write a program in the syntax explained in Sec. 4, ac-

cess our application (the url is shown in Sec. 6) and

upload the ﬁle.

6 CONCLUSIONS

We have presented FleSe, a framework that allows

to enrich regular queries to databases with the use

of fuzzy concepts. FleSe allows the user to perform

fuzzy and non-fuzzy queries to regular databases by

linking the regular non-fuzzy concepts for which we

store values in databases with fuzzy concepts. By do-

ing this we can query the database about fuzzy con-

cepts and the framework will take care of translating

the fuzzy concepts into queries that the database can

answer.

The framework offers to developers a clear syntax

with sound and complete semantics that allows them

to deﬁne satisfaction values for fuzzy concepts from

values stored in databases, from the conﬁguration ﬁle

itself, from the conﬁguration ﬁle when a null value is

found in the database for some individual (or database

row), and from other fuzzy concepts.

A beta version of FleSe is available at

https://fake.url.for.double.blinded.process, where

we have the examples presented here, some others

and the possibility to personalize them and/or include

your own examples. We hope this contribution

helps to improve the existing search mechanisms for

databases, specially the possibility to use human-

oriented attributes (cheap, fast, ...) instead of

computer-oriented attributes (price under X, speed

over Y, ...).

Our current work goes in the direction of offer-

ing via the web interface the possibility to create and

manage the program ﬁles (we only offer now the pos-

sibility to upload them). With this facility any ﬁnal

user could develop his own fuzzy concepts for query-

ing the database, just by knowing database structure

he wants to query.

ACKNOWLEDGEMENTS

This work is partially supported by research projects

DESAFIOS10 (TIN2009-14599-C03-00) funded by

Ministerio Ciencia e Innovaci

on of Spain, PROMETI-

DOS (P2009/TIC-1465) funded by Comunidad

Aut

onoma de Madrid and Research Staff Training

Program (BES-2008-008320) funded by the Spanish

EnrichingTraditionalDatabaseswithFuzzyDefinitionstoAllowFlexibleandExpressiveSearches

117

Ministry of Science and Innovation.

It is partially supported too by the Universi-

dad Polit

ecnica de Madrid entities Departamento

de Lenguajes Sistemas Inform

aticos e Ingenier

ıa de

Software and Facultad de Inform

atica.

REFERENCES

Bobillo, F. and Straccia, U. (2008). fuzzydl: An expres-

sive fuzzy description logic reasoner. In 2008 In-

ternational Conference on Fuzzy Systems (FUZZ-08),

pages 923–930. IEEE Computer Society.

Bosc, P. and Pivert, O. (1995). Sqlf: a relational database

language for fuzzy querying. Fuzzy Systems, IEEE

Transactions on, 3(1):1 –17.

Chen, S.-M. and Jong, W.-T. (1997). Fuzzy query trans-

lation for relational database systems. Systems, Man,

and Cybernetics, Part B: Cybernetics, IEEE Transac-

tions on, 27(4):714–721.

Guadarrama, S., Mu

noz-Hern

andez, S., and Vaucheret, C.

(2004). Fuzzy prolog: a new approach using soft

constraints propagation. Fuzzy Sets and Systems,

144(1):127 – 150.

Herrera-Viedma, E. and L

opez-Herrera, A. (2010). A re-

view on information accessing systems based on fuzzy

linguistic modelling. International Journal of Compu-

tational Intelligence Systems, 3(4):420–437.

Lloyd, J. W. (1987). Foundations of Logic Programming,

2nd Edition. Springer.

Lucarella, D. and Morara, R. (1991). First: Fuzzy informa-

tion retrieval system. Journal of Information Science,

17(2):81–91.

Medina, J., Ojeda-Aciego, M., and Vojt

s, P. (2004).

Similarity-based uniﬁcation: a multi-adjoint ap-

proach. Fuzzy Sets and Systems, 146(1):43–62.

Medina Moreno, J. and Ojeda-Aciego, M. (2002). On ﬁrst-

order multi-adjoint logic programming. In 11th Span-

ish Congress on Fuzzy Logic and Technology.

Morcillo, P. J. and Moreno, G. (2008). Programming

with fuzzy logic rules by using the ﬂoper tool. In

RuleML ’08: Proceedings of the International Sym-

posium on Rule Representation, Interchange and Rea-

soning on the Web, pages 119–126, Berlin, Heidel-

berg. Springer-Verlag.

noz-Hern

andez, S., Pablos-Ceruelo, V., and Strass, H.

(2011). Rfuzzy: Syntax, semantics and implemen-

tation details of a simple and expressive fuzzy tool

over prolog. Information Sciences, 181(10):1951 –

1970. Special Issue on Information Engineering Ap-

plications Based on Lattices.

O’Keefe, R. A. (1990). The Craft of Prolog. The MIT Press.

Pablos-Ceruelo, V. and Mu

noz-Hern

andez, S. (2011). Intro-

ducing priorities in rfuzzy: Syntax and semantics. In

CMMSE 2011 : Proceedings of the 11th International

Conference on Mathematical Methods in Science and

Engineering, volume 3, pages 918–929, Benidorm

(Alicante), Spain.

Ropero, J., Gmez, A., Carrasco, A., and Len, C. (2012).

A fuzzy logic intelligent agent for information ex-

traction: Introducing a new fuzzy logic-based term

weighting scheme. Expert Systems with Applications,

39(4):4567 – 4581.

Sterling, L. and Shapiro, E. (1987). The Art of Prolog. The

MIT Press.

Takahashi, Y. (1991). A fuzzy query language for re-

lational databases. Systems, Man and Cybernetics,

IEEE Transactions on, 21(6):1576–1579.

Theodorakopoulos, G. and Baras, J. S. (2004). Trust eval-

uation in ad-hoc networks. In WiSe ’04: Proceedings

of the 3rd ACM workshop on Wireless security, pages

1–10, New York, NY, USA. ACM.

Tineo, L. J. (2005). A contribution to database ﬂexible

querying: Fuzzy quantiﬁed queries evaluation (PhD.

thesis).

Zadeh, L. A. (1965). Fuzzy sets. Information and Control,

8(3):338–353.

Zadeh, L. A. (1975). The concept of a linguistic variable

and its application to approximate reasoning - i. In-

formation Sciences, 8(3):199–249.

Zadeh, L. A. (2008). Is there a need for fuzzy logic? Infor-

mation Sciences, 178(13):2751–2779.

Zadrony, S. and Nowacka, K. (2009). Fuzzy information

retrieval model revisited. Fuzzy Sets and Systems,

160(15):2173 – 2191. Special Issue: The Application

of Fuzzy Logic and Soft Computing in Information

Management.

Zemankova, M. (1989). Fiis: A fuzzy intelligent informa-

tion system. IEEE Data Eng. Bull., 12(2):11–20.

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

118