
A Non-standard Instance Checking for the Description Logic ELH
Suwan Tongphu and Boontawee Suntisrivaraporn
Information, Computer and Communication Technology, Sirindhorn International Institute of Technology,
Thammasat University, Bangkok, Thailand
Keywords:
Similarity Measure, Description Logic, Degree of Membership, Instance Checking, Non-standard Reasoner.
Abstract:
In Description Logics (DLs), an instance checking is regarded as one of the most important reasoning services
involving individuals. Though the usability of the reasoner has been seemingly proven in many real-life
applications, the classified results are merely a binary response, i.e. whether or not a given individual is an
instance of a concept. As being a standard reasoning service, unsatisfying one among all sufficient conditions
would basically lead to a negative conclusion. This work introduces a new method to enhance the capability
of the instance checking in which the degree of membership could be unveiled though sufficient conditions
are not completely satisfied. The proposed algorithm is developed based on the adoption of a homomorphism
mapping.
1 INTRODUCTION
Representing knowledge in the form that can be uti-
lized by computer agents, known as Knowledge Rep-
resentation, is one challenge field in artificial intelli-
gence. One common formalism is by using a fam-
ily of the knowledge representation called Descrip-
tion Logics (DLs) (Baader et al., 2007). In DLs,
the knowledge is structurally represented by means of
concepts and their relationship. On the one hand, rich
ontologies can be constituted using expressive DLs,
i.e. an employment of the Web Ontology Language
(OWL), which recently becomes a standard seman-
tic web language recommended by W3C consortium.
On the other hand, some other ontologies can alter-
natively be fformulated using lightweight ones which
are sufficiently expressive for the domains and offer
classification tractability, e.g. the use of extensions of
the tractable DL EL in the renowned medical ontol-
ogy (Schulz et al., 2009).
Among a variety of knowledge representation for-
malisms, main reasons making DLs distinct from
others is their underlying reasoning services which
makes implicit knowledge explicit. Apart from the
most prominent subsumption checking service, which
allows finding of subclass-superclass relationship, in-
stance checking is one another readily available ser-
vice, which checks whether a given individual is an
instance of a certain concept. Serving as a standard
service, a classical instance checking gives a posi-
tive response only when sufficient conditions are sat-
isfied; that is, the missing of one of the required con-
cept and/or role assertions consequently turns rea-
soning outputs negative without providing any ben-
eficial clues no matter how rich the assertions are.
This lack leads to an introduction of a non-standard
instance checking service whose response is the de-
gree of membership. In fact, the computation method
is based on a structural homomorphism and is par-
ticularly the extension of our recent work (Suntisri-
varaporn, 2013) on measuring similarity EL concepts.
Hence, the idea is extended to ABox and thus the in-
stance checking problem.
Given an ABox that fulfills all sufficient condi-
tions of a concept description, the proposed algorithm
basically produces the same result as that obtained
from classical reasoners (i.e. both return 1 as the re-
sult). This reflects that, in common cases where suf-
ficient conditions are fulfilled, both standard and the
proposed non-standard algorithm behave in a similar
manner. However, in a situation where not all con-
cept conditions are satisfied. From a classical rea-
soning point of view, as previously mentioned, such
the ABox is normally classified as irrelevant. In con-
trast to the classical reasoners, the proposed algorithm
checks further to an existence of some commonality
and subsequently computes a correspondingdegree of
membership which ranges between 0 and 1.
To be more illustrative, consider an application of
visual object detection proposed in (Tongphu et al.,
2012). In this work, the object of interest (i.e. car ob-
jects) is described by means of its composition (i.e.
67
Tongphu S. and Suntisrivaraporn B..
A Non-standard Instance Checking for the Description Logic ELH.
DOI: 10.5220/0005074900670074
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2014), pages 67-74
ISBN: 978-989-758-049-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
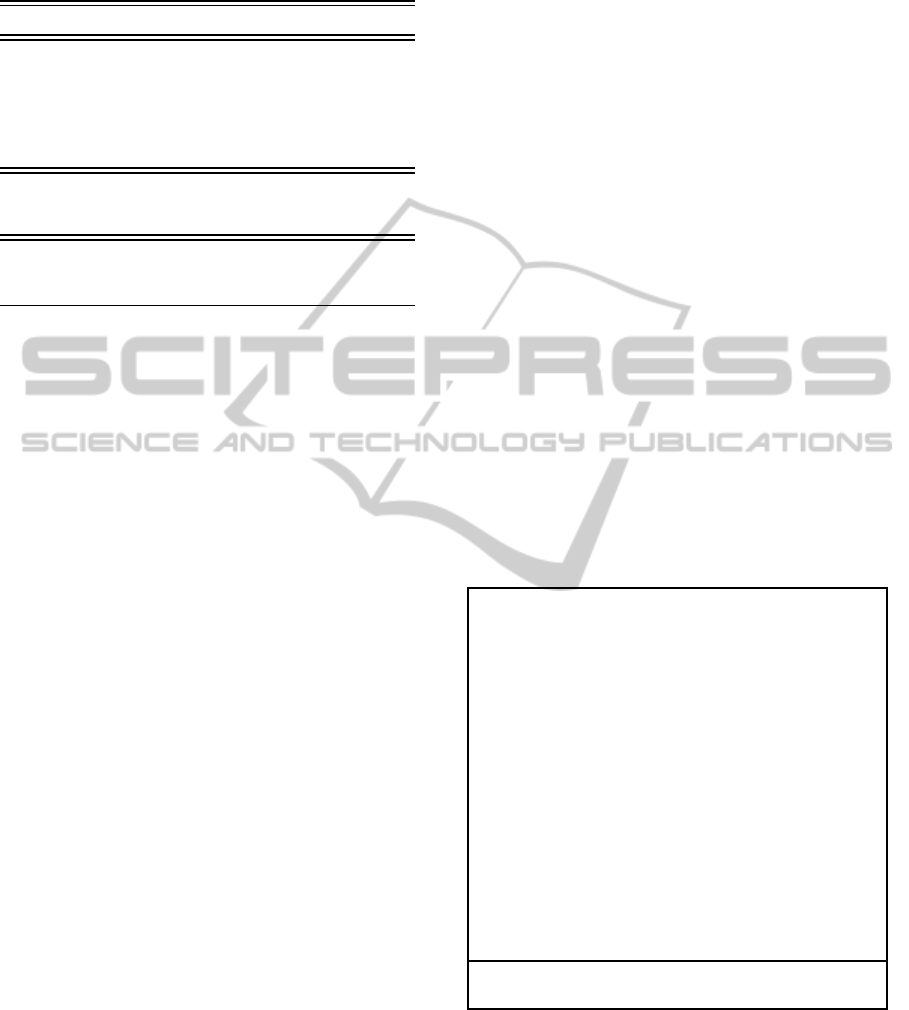
Table 1: Syntax and semantics of the Description Logic
ELH.
Name Syntax Semantics
top ⊤ ∆
I
concept name A A
I
⊆ ∆
I
conjunction C⊓ D C
I
∩ D
I
existential restriction
∃r.C
{x ∈ ∆
I
| ∃y ∈ ∆
I
:
(x,y) ∈ r
I
∧ y ∈ C
I
}
primitive concept def A ⊑ D A
I
⊆ D
I
full concept def A ≡ C A
I
= C
I
concept assertion C(x) x
I
∈ C
I
role assertion r(x, y) (x
I
,y
I
) ∈ r
I
car parts) using an OWL ontology. During a test-
ing stage, visual features extracted from an image are
converted to ontological assertions. By using a clas-
sical instance checking service, the classification re-
sults would basically turn nagative when required car
parts are not entirely detected. The proposed reason-
ing service, on the other hand, returns the degree of
membership based on a shared commonality. This al-
lows a certain cut-off threshold to be set up. The in-
dividual whose degree of membership is greater than
the threshold can then be classified as a car instance.
The rest of this paper is organized in order. The
background on the DL ELH, the unfoldable TBoxes,
and the ELH description tree are described in the
next section. Section 3 and 4 introduce the notions
of the ELH description graph of the assertion ter-
minology and membership homomorphism for the
instance checking problem, respectively. Section 5
and 6 describe related works and give conclusions of
this work.
2 BACKGROUND
In the knowledge representation using the family of
DLs, the concept descriptions of the ELH regarded
as the lightweight DL can be built from a set of primi-
tive concept names CN, a set of role names RN, and a
set of constructors shown in the first part of Table 1. A
finite set of terminological axioms of the form shown
in the second part of Table 1 is called an ELH termi-
nology or TBox. The TBox is said to be unfoldable
if it contains at most one definition for each concept
name, and it is acyclic (i.e. there is no direct or indi-
rect definition refers to the concept itself). For the rest
of this paper, we denote by T an unfoldable TBox.
Let A,B be concept names, and C,D be arbitrary
concept descriptions. For the sake of simplicity, we
denote by CN
def
and CN
pri
, the set of defined concepts
(i.e. the concept that appears on the left-hand side of a
concept description) and the set of primitive concepts
(i.e. the concept that only appears on the right-hand
side of a concept description).
CN = CN
pri
∪ CN
def
Let x and y be individuals, and Ind be a set of in-
dividual names. An ELH ABox A is a finite set of as-
sertions shown in the third part of Table 1. A knowl-
edge base K = (T , A) comprises of T and A.
Like all other DLs, the semantics of ELH is de-
fined by means of interpretations. An interpretation
I = (∆
I
,·
I
) consists of interpretation domain ∆
I
and
interpretation function ·
I
. The interpretation func-
tion maps every concept name A ∈ CN to a subset
A
I
⊆ ∆
I
, every role name r ∈ RN to a binary rela-
tion r
I
⊆ ∆
I
× ∆
I
, and every individual x ∈ Ind to an
element x
I
∈ ∆
I
. The last column of Table 1 depicts
the semantics for ELH constructors, terminological
axioms, and assertions, respectively. An interpreta-
tion I is called a model of the knowledge base K if
it satisfies every axiom in T and every assertion in
A, i.e. conditions in the semantics column of Table 1
are fulfilled. Figure 1 depicts a knowledge base about
family constructed by using DL ELH.
Woman ≡ Female ⊓ Person
Mother ≡ Woman ⊓∃child.Person
GrandMother ≡ Woman ⊓∃child.(Person
⊓ ∃child.Person)
Syster ≡ Woman ⊓ ∃sibling.Person
Aunt ≡ Woman ⊓ ∃sibling.(Person
⊓ ∃child.Person)
Man ≡ Male ⊓ Person
Father ≡ Man ⊓ ∃child.Person
GrandFather ≡ Man ⊓ ∃child.(Person
⊓ ∃child.Person)
Brother ≡ Man ⊓ ∃sibling.Person
Uncle ≡ Man ⊓ ∃sibling.(Person
⊓ ∃child.Person)
Father(a),GrandMother(b), sibling(a,b), sibling(b, a)
Figure 1: Knowledge base of family (K
family
). The termi-
nological box (T
family
) and the examples of assertional box
(A
family
) are shown in the upper part and lower part, respec-
tively.
We assume without loss of generality that an ELH
concept C can be represented using the following
form ((Suntisrivaraporn, 2013)):
KEOD2014-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
68

Algorithm 1: ELH description tree construction.
function build-tree(P
C
,E
C
)
1: Create a new tree T
2: Create a new vertex v ∈ V
3: ℓ(v) ← P
C
4: for each ∃r.C
′
∈ E
C
do
5: build-child-node(v,r, P
C
′
,E
C
′
)
6: return T
function build-child-node(v,r, P
C
,E
C
)
1: Create a new vertex w ∈ V
2: ℓ(w) ← P
C
3: Add a new edge (v,R
r
,w) to E
4: for each ∃s.C
′
∈ E
C
do
5: build-child-node(w, s,P
C
′
,E
C
′
)
P
1
⊓ ··· ⊓ P
m
⊓ ∃r
1
.C
1
⊓ ··· ⊓ ∃r
n
.C
n
where P
i
∈ CN
pri
, r
j
∈ RN, and C
j
are concept de-
scriptions, for 1 ≤ i ≤ m and 1 ≤ j ≤ n. To be more
understandable, consider the concept Aunt defined in
T
family
, the following shows its equivalent expanded
form.
Female ⊓ Person ⊓ ∃sibling.(Person ⊓ ∃child.Person)
For convenience, we denote by P
C
the set of top-level
primitive concepts {P
1
,.. . ,P
m
} and E
C
the set of top-
level existential restrictions {∃r
1
.C
1
,.. . ,∃r
n
.C
n
}. To
handle a role hierarchy, we denote by R
r
= {s|r ⊑
∗
s}
where ∗ is a transitive closure, the set of role expan-
sion w.r.t. r.
We define the ELH description tree of C w.r.t. the
unfoldable TBox by T
C
= (V,E, rt,ℓ) where V is a
set of nodes, E ⊆ V × 2
RN
pri
× V is a set of labeled
edges, rt is a root, and ℓ : V → 2
CN
pri
is a node label-
ing function. Algorithmically, T
C
can be constructed
using Algorithm 1. Figure 2 (left and right) shows an
example of the ELH description tree for the concept
Aunt, written T
Aunt
.
3 REASONING ABOUT
INDIVIDUALS
Given a knowledge base K = (T , A), an individual x
and a concept C, the instance checking problem con-
sists on deciding whether the concept assertion C(x)
is satisfied in every model of K, in symbols K |= C(x),
i.e. x
I
∈ C
I
for every model I of K.
Let Ind(A) denote the set of individuals in A.
In order to enable an investigation for a mem-
bership, a representation of A is transformed into an
ELH description graph G(A) = (V,E, ℓ) whereV de-
Algorithm 2: ELH description graph construction.
function build-graph(A)
1: Create a new graph G = (V, E, ℓ)
2: for each x ∈ Ind(A) do
3: Add v
x
to V
4: for each C(x) ∈ A do
5: ℓ(v
x
) ← P
C
6: V ← V ∪ (V
T
C
\{rt})
7: for each (v, R
r
,u) ∈ E
T
C
do
8: if v 6= rt then
9: Add (v,R
r
,u) to E
10: else
11: Add (v
x
,R
r
,u) to E
12: for each r(x, y) ∈ A do
13: Add (v
x
,R
r
,v
y
) to E
14: return G
notes a set of nodes, E ⊆ V × 2
RN
pri
× V is a set of
labeled edges, and ℓ : V → 2
CN
pri
is a node labeling
function. Algorithm 2 shows a process of the ELH
description graph G(A) construction. Intuitively, for
each individual x defined in A, a corresponding node
v
x
is introduced and added to the graph G(A). For
each C(x) ∈ A, v
x
is augmented by all successors of
the root of T
C
. The outgoing edge that links v
x
to v
y
where r(x,y) ∈ A is then added.
Definition 1 (Homomorphism). Let T and T
′
be two
ELH description trees as defined above. There exists
a homomorphism h from T to T
′
written h : T → T
′
iff the following conditions are satisfied:
1. ℓ(v) ⊆ ℓ
′
(h(v)).
2. For each successor w of v in T, h(w) is a successor
of h(v) with (v, R
r
,w) ∈ E, (h(v),R
s
,h(w)) ∈ E
′
,
and R
r
⊆ R
s
.
Consider A
family
w.r.t. K
family
, the corresponding
ELH description graph for A
family
can be constructed
using Algorithm 2. Figure 2 illustrates an existence
of a homomorphism that maps the root of T
Aunt
to b
in G(A
family
) and a failed attempt to find a homomor-
phism that maps the root of T
Aunt
to a in G(A
family
).
Though the failed mapping does not satisfy the homo-
morphism conditions, there still exists some common-
ality shared between the corresponding nodes and
edges (e.g. both are person and have sibling); that
is, though not being considered as the instance of the
concept, inductively it exhibits some degree of mem-
bership.
Proposition 2 shows the characterization of an in-
stance checking problem by means of an existence of
ANon-standardInstanceCheckingfortheDescriptionLogicELH
69

w
0
: {Person}
a : {Male, Person}
b : {Female,Person}
w
1
: {Person}
w
2
: {Person}
v
0
: {Female, Person}
v
1
: {Person}
v
2
: {Person}
u
0
: {Female,Person}
u
1
: {Person}
u
2
: {Person}
{sibling}
{child}
{sibling}
{child}
{sibling}
{sibling}
{child}
{child}
{child}
×
Figure 2: A homomorphism that maps the root of T
Aunt
(left) to b in G(A
family
) (middle). A failed attempt to map the root
of T
Aunt
(right) to a in G(A
family
).
a homomorphism. It shall turn out that this proposi-
tion can be a generalization for the DL ELH.
Proposition 2. (Baader, 2003) Let T be an EL-TBox,
A an EL-ABox, C a concept in T and x an individual
occurring in A. Then, the following are equivalent:
1. (T , A) |= C(x)
2. There is a homomorphism from the root of T
C
to
x in G(A)
4 MEMBERSHIP
HOMOMORPHISM DEGREE
In addition to the method for computing the member-
ship homomorphism degree originally introduced in
(Suntisrivaraporn, 2013), this work follows the idia
with an extension to handle role hierarchy axioms.
Let C be ELH unfolded concept descriptions, P
C
,
E
C
be as defined in the previoussection, T
C
be the cor-
responding ELH description tree, R
r
and R
s
be sets
of roles w.r.t. the role expansions of r and s, respec-
tively. For convenience, let edge(v) represents the set
of edges from the vertex v, i.e. edge(v) = {(R
r
,w) |
(v, R
r
,w) ∈ E}. Then, the degree of having a mem-
bership homomorphism from rt ∈ T
C
to v ∈ V
G(A)
is
defined as follows:
Definition 3 (Membership Homomorphism Degree).
Let T
T
be the set of all ELH description trees
from TBox T and V
G(A)
be the set of all ver-
tices in the description graph from ABox A.
The membership homomorphism degree function
mh : T
T
×V
G(A)
→ [0, 1] is inductively defined as
follows:
mh(T
C
,v ∈ V
G
) := µ· p-mh(P
C
,ℓ(v))
+(1− µ) · e-set-mh(E
C
,edge(v)),
(1)
where 0 ≤ µ ≤ 1;
p-mh(P
C
,ℓ(v)) :=
(
1 if P
C
=
/
0
|P
C
∩ℓ(v)|
|P
C
|
otherwise,
(2)
where | · | represents a set cardinality;
e-set-mh(E
C
,E) :=
∑
ε∈E
C
max{e-mh(ε,e):e∈E}
|E
C
|
,
(3)
where ε is an existential restriction, e is an edge, and
E ⊆ E
G(A)
is a set of outgoing edges; and
e-mh(∃r.X, (R
s
,w)) :=
γ(ν+ (1− ν) · mh(T
X
,w))
(4)
where γ =
|R
r
∩R
s
|
|R
r
|
and 0 ≤ ν < 1.
The meaning of the parameters µ and ν are sim-
ilar to those defined in (Suntisrivaraporn, 2013) and
set to
|P
C
|
|P
C
∪E
C
|
and 0.4, respectively. The value of γ in
Formula 4 is a proportion of a set of common roles
against all those respect to r. For the case where
γ = 0, this means there is no commonality between
two given roles r and s, i.e. further computations for
the degrees of membership among their successors
should be omitted. If 0 < γ ≤ 1, this reveals that there
exists some commonality. However, in the case where
γ = 1, both r and s are totally similar and thus consid-
ered logically equivalent.
KEOD2014-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
70

Algorithm 3: ELH similarity measure.
function mh(T
C
,v ∈ V
G(A)
)
1: i ← µ· p-mh(P
C
,ℓ(v)) +
(1− µ)e-set-mh(E
C
,edge(v))
2: return i
function p-mh(P
C
,ℓ(v))
1: if P
C
←
/
0 then
2: return 1
3: else
4: return
|P
C
∩ℓ(v)|
|P
C
|
function e-set-mh(E
C
,E ⊆ E
G(A)
)
1: sum ← 0
2: for each ε ∈ E
C
do
3: max ← 0
4: for each e ∈ E do
5: if e-mh(ε,e) > max then
6: max ← e-mh(ε,e)
7: sum ← sum+
max
|E
C
|
8: return sum
function e-mh(∃r.X, (R
s
,w))
1: if γ = 0 then
2: return 0
3: else
4: return γ(ν+ (1− ν) · mh(T
X
,w))
Proposition 4. Providing a description graph G(A)
w.r.t. A and an ELH description tree T
C
of a concept
C in an unfoldable ELH TBox T , the followings are
equivalent:
1. (T , A) |= C(x)
2. mh(T
C
,v
x
∈ G(A)) = 1
Proof. (1 =⇒ 2) By Proposition 2, C(x) ∈ A
then there exists a homomorphism mapping rt ∈ T
C
to v
x
∈ V
G(A)
. For the induction base case where
the depth of T
C
is zero (i.e. T
C
contains only one
node), by Definition 3, this inductively implies that
ℓ(rt) ⊆ ℓ(v
x
), such that µ = 1, and p-mh(P
C
,ℓ(v
x
)) =
1 and as a consequence mh(T
C
,v
x
∈ V
G(A)
) = 1. For
the induction step where the depth of T
C
is nonzero,
for every v ∈ V
T
C
there exists h(v) ∈ V
G(A)
such
that ℓ(v) ⊆ ℓ(h(v)) (i.e. p-mh(·, ·) = 1) and for every
(v, R
r
,w) ∈ E
T
C
there exists (h(v),R
s
,h(w)) ∈ E
G(A)
where w and h(w) are successors of v and h(v), re-
spectively, such that R
r
⊆ R
s
(i.e. e-set-mh(·,·) = 1).
Hence, mh(T
C
,v
x
∈ V
G(A)
) = 1.
(2 =⇒ 1) By Definition 3, mh(T
C
,v
x
∈ V
G(A)
) = 1
means mh(·, ·) = 1 and e-set-mh(·, ·) = 1) (in case that
the tree has child nodes) such that two conditions of
a homomorphism defined in Definition 1 are satisfied
and by Proposition 2, C(x) ∈ A.
The membership homomorphism function unveils
a numerical value measuring the degree membership
of an individual in an ABox description graph against
a compared concept description tree. Intuitively, this
infers the degree of membership which suggests how
close an individual is an instance of a concept. There-
fore, we define the degree of membership of the indi-
vidual x to the concept C as the numerical value ob-
tained from mh(T
C
,v
x
∈ V
G(A)
).
Example 5. To illustrate how the algorithm works,
consider the expanded description tree T
Aunt
and the
expanded description graph G(A
family
) shown in Fig-
ure 2, using µ and ν as previously described, the de-
grees of membership of the individual a to the con-
cept Aunt can be computed using Algorithm 3. The
following shows computation steps:
mh(T
Aunt
,v
a
∈ V
G
)
:=
2
3
p-mh(P
Aunt
,ℓ(v
a
))
+
1
3
e-set-mh(E
Aunt
,edge(v
a
))
:=
2
3
(
1
2
) +
1
3
(γ(ν+ (1 − ν)
·mh(T
Person⊓∃ch.Person
,v
b
)))
:=
2
3
(
1
2
) +
1
3
(1(
2
5
+
3
5
mh(T
Person⊓∃ch.Person
,v
b
)))
// where mh(T
Person⊓∃ch.Person
,v
b
) yields 1;
// see belows
:=
2
3
(
1
2
) +
1
3
(1(
2
5
+
3
5
(1)))
:=
2
3
:= 0.667
The computation for the sub-description correspond-
ing to v
1
and b in Figure 2 is as follows:
mh(T
Person⊓∃ch.Person
,v
b
∈ V
G
)
:=
2
3
p-mh(P
Person⊓∃ch.Person
,ℓ(v
b
))
+
1
3
e-set-mh(E
Person⊓∃ch.Person
,edge(v
b
))
:=
1
2
(
1
2
) +
1
2
e-set-mh(E
Person⊓∃ch.Person
,edge(v
b
))
// where e-set-mh(E
Person⊓∃ch.Person
,edge(v
b
))
// yields 1; see belows
:=
1
2
(1) +
1
2
(1) := 1
The computation for the sub-description correspond-
ing with ε = ∃child.Person and e = ({child}, v
w
1
) is
as follows:
ANon-standardInstanceCheckingfortheDescriptionLogicELH
71

e-mh(ε,e)
:= γ(ν+ (1 − ν)mh(T
Person
,v
w
1
∈ V
G
))
:= 1(
2
5
+
3
5
mh(T
Person
,v
w
1
∈ V
G
))
:=
2
5
+
3
5
(1) := 1
The computation for the alternative sub-description
corresponding with ε = ∃child.Person and e =
({sibling}, v
a
) is, however, equal to 0 since γ = 0.
That is max(e-mh(ε,e)) = 1.
Table 2: The degrees of membership of all concepts in
T
family
to the individual a and b.
Concept Names
Degrees of membership
a b
Woman 0.5 1.0
Mother 0.667 1.0
GrandMother 0.567 1.0
Sister 0.667 1.0
Aunt 0.667 1.0
Man 1.0 0.5
Father 1.0 0.667
GrandFather 0.9 0.667
Brother 1.0 0.667
Uncle 1.0 0.667
By applying the same computation approach to the
rest of all defined concepts w.r.t. T
family
, Table 2 shows
the degrees of membership of the individual a and b
to all defined concepts.
Providing that a is an instance of Father, and a
is a sibling of b, the degrees of membership, ob-
tained through the proposed algorithm together with
Proposition 4, reveal that a is also an instance of
Man, Brother, and Uncle. Likewise, b is not only
an instance of GrandMother but also an instance of
Woman, Mother, Sister, and Aunt.
Apart from a crisp response, the proposed ser-
vice is yet capable of inductively unveiling the de-
grees of membership though the two stated conditions
of being homomorphism are not completely satisfied.
For example, consider the degrees of membership
of a to the concept GrandFather and GrandMother.
Though a is not considered as an instance of either
concepts in view of classical instance checking, intu-
itively, it is reasonable to argue that a is more similar
to GrandFather than GrandMother (see e.g. the de-
grees of membership of 0.9 and 0.567, respectively).
5 RELATED WORKS
In DLs, prominent reasoning services conern con-
cepts are concept subsumption and concept satis-
fiability; whereas those concerning individuals are
instance checking and instance retrieval. Often-
times, instance checking algorithms have obtained
from adaptation of existing algorithms for concept
subsumption and satisfiability (Baader et al., 2003;
Baader and Sattler, 2001). In a sense, studying on
concept similarity measures is a natural approach to
solving instance checking problem.
Measuring degreesof membership as well as simi-
larity in DLs have been intensively studied in the past
few decades with a number of great attempts. The
computation methods can be, however, broadly cat-
egorized into two major approaches. One is simply
focused on a structural distance (Batet et al., 2010;
Schickel-Zuber and Faltings, 2007; Blanchard et al.,
2005; Passant, 2010) which normally ignores the se-
mantics. The other try to semantically analyze the
relationship among concepts and to inductively com-
pute the degree of membership based on the defined
description itself. Our approach is in the second cate-
gory. The following describes major related papers.
Stuckenschmidt adopts the algorithm (Stucken-
schmidt, 2009) originally introduced by Champin et
al. (Champin and Solnon, 2003). The algorithm
measures a similarity between concept instances by
analyzing the degrees of commonality between the
graphs of two concept instances. The proposed algo-
rithm however ignores a deliberation of a subsump-
tion relation. Hence, instances of different concepts
are always identified as dissimilar.
Amato et al. (d’Amato et al., 2006) propose a
method measuring a semantic similarity between con-
cepts and instances. In this work, the degrees of mem-
bership are based on a counting of concept member-
ship (i.e. a counting for instances of concepts). The
estimation is then inductively computed using the k-
Nearest Neighbor (k-NN) method. One disadvantage
of this method is an undecidable concept membership
could be possibly found, i.e. the individual cannot be
determined whether it is an instance of a certain con-
cept.
Bianchini et al. (Bianchini et al., 2005) propose
a hybrid method that combines a deductive match-
ing method with constraints (Li and Horrocks, 2003)
and a semantic-based matching method. The degree
of similarity is numerical measured with a big range
of similarity coefficient which turns the analysis of a
similarity measure among a number of concepts be-
comes a difficult task.
A probabilistic variant of description logic has
been introduced in (Fagin et al., 1990) and partially
implemented in the Pronto system (Klinov, 2008). In-
stead of merely stating crisp axioms and assertions,
the probabilistic inference engine Pronto allows an
KEOD2014-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
72

existence of a probabilistic TBox and ABox. One ob-
vious drawback of Pronto is that all sufficient condi-
tions of a concept description must be satisfied. Un-
like Pronto, our algorithm requires neither a fulfill-
ment of concept conditions nor a probabilistic asser-
tion.
The work on a similarity measure for the DL
ELH proposed by Lehman and Turhan (Lehmann and
Turhan, 2012) introduces a new similarity framework
that allows tuning of various parameters. Our ap-
proach is similar to this work.
6 CONCLUSION AND FUTURE
WORKS
This work presents an attempt to measure the degree
of membership of an individual to a compared con-
cept. The capability of the proposed reasoning ser-
vices is devised to handle the case where necessary
conditions are not completely satisfied, but there ex-
ists some commonality. The instance checking prob-
lem is, thus, rather resolved by means of the numer-
ical degree of membership. The usability of the pro-
posed algorithm is demonstrated through the well-
known terminology of family. The examples simply
depict a common case of the individuals that could
possibly be found in such the assertional terminology.
As being speculated as common steps for future
works, it would be beneficial to extend the proposed
method to be supported on more expressive DLs as
well as to increase a capability of handling the con-
cepts w.r.t. general TBoxes (i.e. cyclic TBoxes).
It is to be mentioned that with a pre-processing
of a concept description expansion, the complexity of
the algorithm is polynomially bounded and directly
variant to the depth of a concept description tree and
an ABox description graph. However, the expansion
process itself can be dramatically grown in an expo-
nential time. Fortunately, this can be handled through
a representation of an entire TBox as a forest of inter-
dependent ELH description trees.
REFERENCES
Baader, F. (2003). The instance problem and the most spe-
cific concept in the description logic EL w.r.t. termi-
nological cycles with descriptive semantics. In Gnter,
A., Kruse, R., and Neumann, B., editors, KI, volume
2821 of Lecture Notes in Computer Science, pages
64–78. Springer.
Baader, F., Calvanese, D., McGuinness, D., Nardi, D., and
Patel-Schneider, P., editors (2007). The Description
Logic Handbook: Theory, Implementation and Appli-
cations. Cambridge University Press, second edition.
Baader, F., Hladik, J., Lutz, C., and Wolter, F. (2003). From
tableaux to automata for description logics. Funda-
menta Informaticae, 57(2-4):247–279.
Baader, F. and Sattler, U. (2001). An overview of tableau
algorithms for description logics. Studia Logica,
69(1):5–40.
Batet, M., Valls, A., and Gibert, K. (2010). A distance func-
tion to assess the similarity of words using ontologies.
XV Congreso Espaol sobre Tecnologas y Lgica Fuzzy
(ESTYLF), 10:561–566.
Bianchini, D., Antonellis, V. D., and Melchiori, M. (2005).
Capability matching and similarity reasoning in ser-
vice discovery. In Missikoff, M. and 0001, A.
D. N., editors, EMOI-INTEROP, volume 160 of
CEUR Workshop Proceedings. CEUR-WS.org.
Blanchard, E., Harzallah, M., Briand, H., and Kuntz, P.
(2005). A typology of ontology-based semantic mea-
sures. In Proceedings of the Open Interop Workshop
on Enterprise Modelling and Ontologies for Interop-
erability.
Champin, P. A. and Solnon, C. (2003). Measuring the sim-
ilarity of labeled graphs. In Ashley, K. D. and Bridge,
D. G., editors, 5th International Conference On Case-
Based Reasoning (ICCBR 2003), LNAI, pages 80–95.
Springer.
d’Amato, C., Fanizzi, N., and Esposito, F. (2006). Reason-
ing by analogy in description logics through instance-
based learning. In Semantic Web Applications and
Perspectives, volume 201 of CEUR Workshop Pro-
ceedings.
Fagin, R., Halpern, J. Y., and Megiddo, N. (1990). A logic
for reasoning about probabilities. Information and
Computation., 87(1-2):78–128.
Klinov, P. (2008). Pronto: A non-monotonic probabilistic
description logic reasoner. In Proceedings of Euro-
pean Semantic Web Conference (ESWC), pages 822–
826.
Lehmann, K. and Turhan, A.-Y. (2012). A framework
for semantic-based similarity measures for ELH -
concepts. In del Cerro, L. F., Herzig, A., and Mengin,
J., editors, JELIA, volume 7519 of Lecture Notes in
Computer Science, pages 307–319. Springer.
Li, L. and Horrocks, I. (2003). A software framework
for matchmaking based on semantic web technology.
In 12th international conference on World Wide Web,
pages 331–339. ACM Press.
Passant, A. (2010). Measuring semantic distance on linking
data and using it for resources recommendations. In
AAAI Spring Symposium: Linked Data Meets Artifi-
cial Intelligence.
Schickel-Zuber, V. and Faltings, B. (2007). Oss: A seman-
tic similarity function based on hierarchical ontolo-
gies. In Proceedings of the 20th International Joint
Conference on Artifical Intelligence, IJCAI’07, pages
551–556, San Francisco, CA, USA. Morgan Kauf-
mann Publishers Inc.
Schulz, S., Suntisrivaraporn, B., Baader, F., and Boeker, M.
(2009). SNOMED reaching its adolescence: Ontolo-
ANon-standardInstanceCheckingfortheDescriptionLogicELH
73

gists’ and logicians’ health check. International Jour-
nal of Medical Informatics, 78(Supplement 1):S86–
S94.
Stuckenschmidt, H. (2009). A semantic similarity measure
for ontology-based information. In Flexible Query
Answering Systems, pages 406–417. Springer.
Suntisrivaraporn, B. (2013). A similarity measure for the
description logic E L with unfoldable terminologies.
In International Conference on Intelligent Networking
and Collaborative Systems (INCoS-13), pages 408–
413.
Tongphu, S., Suntisrivaraporn, B., Uyyanonvara, B., and
Dailey, M. N. (2012). Ontology-based object recog-
nition of car sides. In 9th International Con-
ference on Electrical Engineering/Electronics Com-
puter Telecommunications and Information Technol-
ogy (ECTI).
KEOD2014-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
74
