Prediction Model Adaptation Thanks to Control Chart Monitoring

Application to Pollutants Prediction

Philippe Thomas, William Derigent and Marie-Christine Suhner

Université de Lorraine, CRAN, UMR 7039, Campus Sciences, BP 70239, 54506 Vandœuvre-lès-Nancy cedex, France

CNRS, CRAN, UMR7039, 54506 Vandœuvre-lès-Nancy cedex, France

Keywords: Indoor Air Quality, Neural Networks, Relearning, Control Charts.

Abstract: Indoor air quality is a major determinant of personal exposure to pollutants in today’s world since people

spend much of their time in numerous different indoor environments. The Anaximen company develops a

smart and connected object named Alima, which can measure every minute several physical parameters:

temperature, humidity, concentrations of COV, CO

, formaldehyde and particulate matter (pm). Beyond the

measurement aspect, Alima presents some data analysis feature named ‘predictive analytics’, whose

primary aim is to predict the evolution of indoor pollutants in time. In this article, the neural network (NN)

model, embedded in this object and designed for pollutant prediction, is presented. In addition with this NN

model, this article also details an approach where batch learning is performed periodically when a too

important drift between the model and the system is detected. This approach is based on control charts.

1 INTRODUCTION

Air pollution is now identified as a major

international issue. However, in people’s mind, it

always refers to the quality of outdoor air, whereas

the predominant environment in this regard is the

residence. Indeed, indoor air quality is a major

determinant of personal exposure to pollutants in

today’s world since people spend much of their time

in numerous different indoor environments (Walsh

et al. 1987).

During the last two decades there has been

increasing concern within the scientific community

over the effects of indoor air quality on health.

Changes in building design devised to improve

energy efficiency have meant that modern homes

and offices are frequently more airtight than older

structures. Furthermore, advances in construction

technology have caused a much greater use of

synthetic building materials, which provide indoor

pollution (Jones 1999).

The known health impacts and corresponding

pollutants are numerous. Table 1 is an excerpt taken

from (Spengler and Sexton, 1983) to illustrate some

of the major indoor pollutants. The sources of

pollution can be located indoor (building material,

furniture, stoves…) or outdoor (air coming through

an opened window or via the ventilation system).

Table 1: Pollutants and sources.

Pollutant Major emission sources

Allergens House dust, domestic animals,

Asbestos Fire retardant materials, insulation

Carbon dioxide Metabolic activity, combustion activities,

Carbon monoxide Fuel burning, boilers, stoves, gas…

Formaldehyde Particleboard, insulation, furnishings

Micro-organisms People, animals, plants, air conditioning

Nitrogen dioxide Outdoor air, fuel burning, motor vehicles

Organic substances Adhesives, solvents, building materials,

Ozone Photochemical reactions

Particles Tobacco smoke, combustion products...

Polycyclic aromatic

hydrocarbons

Fuel combustion, tobacco smoke

Pollens Outdoor air, trees, grass, weeds, plants

Radon Soil, building construction materials

(concrete, stone)

Fungal spores Soil, plants, foodstuffs, internal surfaces

Sulfur dioxide Outdoor air, fuel combustion

Symptoms and consequences of exposure to a

pollutant can vary depending on the pollutant type

and concentration. For example, the carbon dioxide

(whose indoor concentrations can vary from 700 to

3000 ppm) is a simple suffocating gas and can also

act as a respiratory irritant (Maroni et al. 1995),

whereas the exposition to a formaldehyde

concentration of 100 ppm can cause death.

It thus explains why indoor air quality recently

receives much public attention, and people are now

eager to measure in their own homes the quality of

their indoor air. To answer to this growing need, The

Anaximen Company develops a smart and

172

Thomas P., Derigent W. and Suhner M..

Prediction Model Adaptation Thanks to Control Chart Monitoring - Application to Pollutants Prediction.

DOI: 10.5220/0005075501720179

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 172-179

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

connected object named Alima (Alima, 2013).

In fact, pollutant levels are constantly changing,

depending on the tenants’ activities. Alima can

measure every minute several physical parameters:

temperature, humidity, concentrations of COV, CO

formaldehyde and particulate matter (pm). Data are

stored on the object or can be sent to a distant

database, and are available for the user online via

phone apps or websites. Beyond the measurement

aspect, the society currently plans to embed in Alima

some data analysis feature named ‘predictive

analytics’, whose primary aim is to predict the

evolution of indoor pollutants in time. Anaximen

and the CRAN laboratory are associated to develop

this leading-edge feature.

In this article, a neural network (NN) model

designed for pollutant prediction is presented.

However, a drift can appear between the NN model

and the system modelled (due to, for example, a

modification of the occupant behavior), and forces

the NN to do a relearning phase. But this relearning

phase is time and resource consuming and should be

done sparingly. So, in addition with the NN model

for pollutant detection, this article also details an

approach where batch learning is performed

periodically when a too important drift between the

model and the system is detected. This approach is

based on control charts.

Section 2 presents a short state-of-the-art on neural

network modelling, section 3 details the approach

used to control the drift and perform the batch

learning while section 4 presents the industrial

application. Section 5 first exposes the results

obtained by the NN model for pollutant prediction

(without any relearning phase), and then describes

the results obtained when using the drift detection

algorithm.

2 NEURAL NETWORK MODEL

Artificial neural network models have been

successfully applied to solve many different

problems, including dynamic systems identification,

patterns classification, adaptive control, functions

approximation and so on.

Among these artificial neural network models, the

multilayer perceptron (MLP) is, by far, the most

popular architecture due to its structural flexibility,

good representational capabilities, and the

availability of a large number of training algorithms

(Han and Qiao 2013). This model is used for both

classification and regression tasks.

Works of Cybenko (1989) and Funahashi (1989)

have proved that a MLP with only one hidden layer

using a sigmoïdal activation function and an output

layer can approximate all non-linear functions with

the wanted accuracy. Its structure is given by:

2101

iihhi

zg wg wx b b















(1)

Where:

are the n

inputs of the neural network,

are the weights connecting the input layer

to the hidden layer,

b are the biases of the hidden neurons,

(.) is the activation function of the hidden

neurons (namely the hyperbolic tangent),

w are the weights connecting the hidden

neurons to the output one,

b is the bias of the output neuron,

- g

(.) is the activation function of the output

neuron and,

z is the network output.

Because the problem is a regression problem, g

(.) is

chosen linear.

Three steps must be performed in order to design the

neural model:

initialization, learning and pruning.

The first one is the determination of the initial set of

weights and biases. This step is important because

learning algorithm performs a local search of the

minimum. So, in order to avoid local minimum

trapping, different initial sets must be constructed

which allow beginning to learn in different zones of

the criteria domain. Different initialization

algorithms have been proposed in the literature

(Thomas and Bloch 1997). The initialization

algorithm used in this paper is the one proposed by

Nguyen and Widrow (1990) which allows

associating a random initialization of weights and

biases to an optimal placement in input and output

spaces.

The second step is performed by the learning

algorithm which must fit the network output with the

data. In industrial applications, data are noisy and

corrupted with many outliers. In order to limit the

impact of outliers on the results, a robust Levenberg-

Marquardt algorithm is used (Thomas

et al. 1999).

Levenberg–Marquard algorithm allows associating

the speed of the Hessian methods to the stability of

the gradient methods. This is performed by adding a

parameter multiplied by the identity matrix in order

to permit the inversion of the Hessian matrix even if

it is singular. The tuning of this parameter during the

learning allows the Levenberg–Marquard algorithm

to work as a gradient descent algorithm when this

PredictionModelAdaptationThankstoControlChartMonitoring-ApplicationtoPollutantsPrediction

173

parameter is large and as a Gauss–Newton algorithm

when this parameter is small. The use of a robust

criterion allows to avoid the influence of outliers and

provides a regularization effect in order to prevent

overfitting. An important issue in neural network

design is the determination of its structure. To

determine it, two approaches can be used. The first

one is constructive, where the hidden neurons are

added one after the other (Ma and Khorasani 2004).

The second approach exploits a structure with too

many initial hidden neurons, and then prunes the

least significant ones (Setiono and Leow 2000,

Engelbrecht 2001). We focus on the pruning

approach that allows a simultaneous selection of the

input neurons and the number of hidden neurons.

The pruning phase is performed in two steps. First,

the Engelbrecht algorithm is used which allows to

quickly simplify the structure and second, the

Setiono and Leow algorithm is used which is slower

but also more efficient (Thomas

et al. 2013).

3 ONLINE ADAPTATION OF THE

MODEL

3.1 Generalities

Ideally, the data collected during the

experimentation phase should describe all the states

of the system to model. However, it is sometimes

not feasible due to the high number of potential

situations the system could encounter. Indeed, in our

case data collected are different depending on the

seasons, the yearly weather, changes in user’s habits

and so on. Technically, it would thus be highly

difficult to obtain an exhaustive data set. As a result,

our approach consists in two phases: first, a learning

phase is achieved based on a data set obtained via a

relatively short experimentation phase (in our case, 1

month, see section 4.1) to construct a first “specific”

NN model. Then, a relearning is launched if and

only if a significant difference (called “drift”)

between the system behavior and its corresponding

NN model is detected.

In many case, a drift may appear between the model

constructed and the system studied. This drift may

be due to two main reasons. The first one concerns

the evolution of input parameters. With a learning

approach, the obtained model is valid only on the

learned domain. The model is able to provide a valid

solution only in this concerned domain.

The second reason concerns the uncontrolled

modification of the machine or environment

behavior. Indeed, A change of a parameter

(voluntarily or not, measured or not) which is not an

input of the model, can affect the behavior of the

machine. In this case, this parameter should be part

of the model inputs but, as it was considered

constant for the duration of the learning step, it was

not retained as such. Due to this change, which may

even be unknown to operators and users, the model

will therefore provide results out of step with reality.

To take into account these problems, a relearning

on new data is needed. There are two practical ways

to implement learning in neural networks: batch

training and on-line training. Whenever a new data

is received, batch learning uses this new data

together with the past data to perform a retraining.

But this approach is time consuming. The on-line

approach uses only new data to adapt the model.

However, this approach suffers from slow training

error convergence as a large number of training data

may be required (Liang

et al. 2006). Moreover,

different works have shown that on-line training

strategy does not converge to the optimal weights

(Heskes and Wiegerinck 1996, Nakama 2009).

We thus propose here another approach where a

batch learning is performed periodically when a drift

between the model and the system occurs, in order

to synchronize the model with the reality.

Because this synchronization is time consuming, the

synchronization frequency must be optimized.

Rather than consider a resynchronization frequency

in response to events (arrival of new information

from one of the connected devices, solicitation by an

operator…) or a periodically one (every hour,

week…), it is better to rely on statistical findings.

Among the 7 basic tools for quality control, control

charts, also known as Shewhart charts or process-

behavior charts (Shewhart 1931), are interesting

Statistical Process Control (SPC) tools useful for our

proposed system.

3.2 Control Charts

Control charts are particularly relevant to the

dynamic quality control with the use of time-series

(Tague 2004). They can determine statistically if a

variation is no longer under control. Indeed, it is

known that even when a process is under control

there is approximately a 0.27% probability of a point

exceeding a 3σ control limit (Pareto). These few

isolated points should not trigger synchronization.

But the detection of too many points above this limit

may underlines the presence of a special cause, even

if it is not yet known.

The Combination of a neural network with the

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

174

control charts can therefore inherit from the

robustness of the statistical analysis and the

adaptability of the neural network. Du

et al. (2012)

work on the inverse combination of both tools with a

recognition algorithm of control charts using neural

networks to get alerts in case of quality problems

and to provide clues in defining causes.

In our case, when a set of

n new data is collected,

a performance indicator is calculated and compared

to two bounds determined on the initial validation

data set. If this indicator is still between the two

bounds, the model is always suitable. If the new

value of the indicator is outside the bounds, a

relearning phase is needed on these new collected

data. Figure 1 shows an example of control chart to

monitor the accuracy of the model. It presents the

evolution of the considered indicator compared to

the upper (UCL) and lower bounds (LCL) in

function of samples of size

n. In this example, the

two first samples present acceptable results and the

model accuracy is sufficient. For the third sample,

the indicator is outside the bounds and a relearning

on the

n last data is needed to drive the indicator

inside the bounds for the next samples. If no

relearning occurs, the drift between model and

reality stays and may grow.

1 2 3 4 sample

LCL

UCL

indicator

With relearning

Without relearning

Figure 1: Example of control chart used for monitoring

accuracy of the model.

3.3 Control Bounds

Our control charts (s charts) aim to determine if a

process characteristic is stable. The center line (CL)

is given by the standard deviation of the considered

characteristics. The Upper Control Limit (UCL) and

the Lower Control Limit (LCL) are calculated for

representing 99.8% of data (NIST/SEMATECH

2012). These limits are given by:

UCL s c

CL s

CL s c



 









 





(2)

where:

stands for the center line (CL) and

correspond to the estimated standard deviation

of the characteristic monitored,

n is the size of the sample,

is a factor allowing to find an unbiased

estimator of the standard deviation





(3)

With c

given by:





















(4)

where the non-integer factorial is given by:

!.1.2 .

222 2 2

nnn n



    



    

    



(5)

In the considered case, the monitored characteristic

is the error performed by the network, and so, the

parameter to monitor is the sample standard

deviation given by:















(6)

where



stands for the error performed on data i and



stands for the mean of the error.

The value of the estimated standard deviation

obtained on the validation data set used to validate

the initial model.

4 INDUSTRIAL APPLICATION

4.1 Description of the Case Study

The experimentation site is a single storey dwelling

whose floor plan is shown figure 2.

ROOM1

ROOM2

ROOM3

ROOM4

LIVINGROOM

GARAGE

KITCHEN

BATHROOM

LAUNDRY

Figure 2: Implantation of the 5 Alima in a house.

PredictionModelAdaptationThankstoControlChartMonitoring-ApplicationtoPollutantsPrediction

175

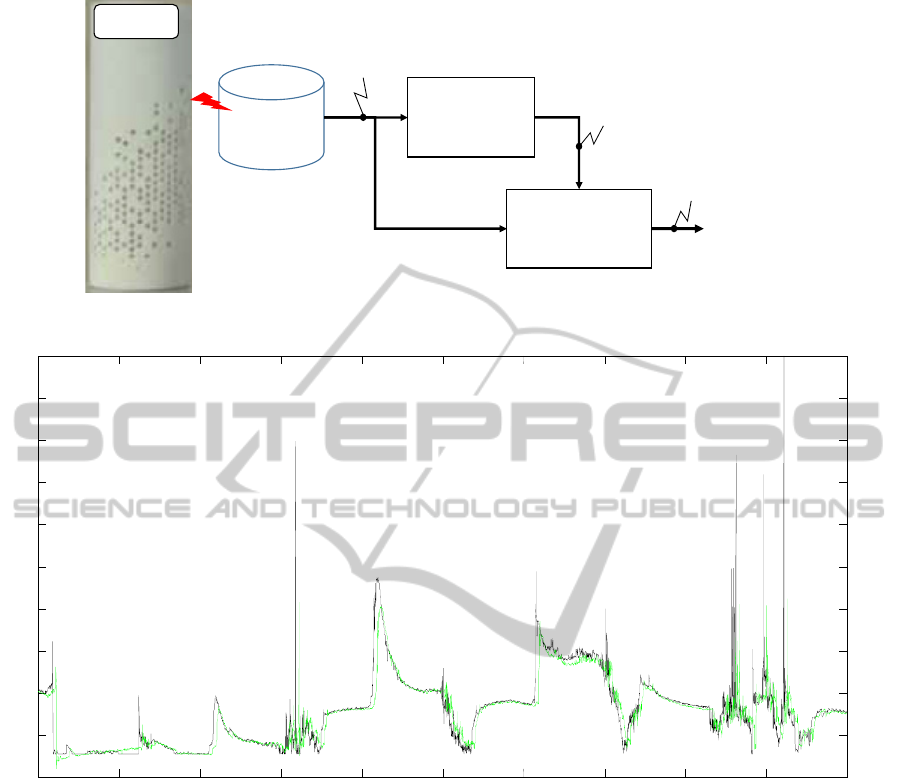
database

Classification

model

Prediction

model

REDICTION

MINUTES

ALIMA

Current situation

Parameter values

Figure 3: Pollutant prediction principle.

0 1 2 3 4 Day

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 4: prediction of C0

Red points indicate the different locations of the 5

Alimas installed in the house. The experimentation

ran during a period of 1 month during summer 2013,

and Alimas were recording each minute the values

of their different sensors. The data set is divided in

two subsets (learning and validation data set) each

corresponding to 15 days of collected data. Only

data collected by Alima1 are used for the learning

and validation.

4.2 Considered Problem

We focus here on the problem of pollutant evolution

prediction. As explain previously, each Alima

collects, each minute, the values of five parameters

(temperature, humidity, CO

, COV and particulate

matter (pm)). The goal is to predict 30 minutes

ahead the level of each pollutant in function of the

actual and past level of these pollutants. In order to

improve the performance of the model, different

situations (cooking, sleeping…) are detected by

using a classification model. The output of this

classification model is used as an input of the

prediction model.

The figure 3 presents the principle of the prediction

of pollutants. The database collects data from the

Alima. These data are use in a first step in order to

detect the current situation (cooking, sleeping…)

which may have an impact on the pollutant

evolution. The design of the classification model has

already been submitted to the MOSIM2014

conference. This article is thus entirely focused on

the prediction model. This model takes as inputs the

8 actual outputs of the classification model and the 5

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

176

past values (

t, t-1, t-2, t-3, t-4) of the parameters

collected by Alima. Three different models are built

for each pollutant (CO

, COV, pm). The output of

the considered model is the value of the considered

pollutant 30 minutes later (

t+30). In order to avoid

the local minimum trapping, the learning is

performed on 20 different initial parameters sets.

The data set is divided in two subsets (learning and

validation data set) each corresponding to 15 days of

collected data. Only data collected by Alima1 are

used for the learning and validation. A pruning

algorithm is used in order to avoid the overfitting

problem. At last, the best resulting model is selected.

5 RESULTS

5.1 Results Obtained on the Validation

Data Set

In a first step, the results obtained on the validation

data set are presented. Figure 4 presents the

prediction of CO

(in green) to compare to the real

values collected (in black). This figure shows that

the evolution of CO2 level may be predicted with a

good accuracy even if the amplitude of the larger

variation can’t be predicted.

The figure 5 presents the prediction error for the

pollutant (for the first 5 days of the validation

data set). This figure shows that the model is able to

predict the smooth evolution but it is not able to find

the total amplitude of greatest variations. For these

two figures, the data are normalized due to

confidential needing. However, the model works

with the true range of variation.

0 1 2 3 4 Day

-0.4

-0.2

0.2

0.4

0.6

0.8

Prediction

Error on CO

Figure 5: prediction error of C0

The results obtained for the COV pollutant is

quite similar and are not presented here.

Figure 6 and 7 present the same results obtained

for pm pollutants.

These two figures show that pm is corrupted with

an important noise. The events to detect have an

amplitude of the same order to the noise variance.

0 1 2 3 4 Day

0.65

0.7

0.75

0.8

0.85

0.9

0.95

Figure 6: prediction of pm.

However, the model is able to predict the evolution

of the pm pollutant with a good accuracy.

5.2 Adaptation of the Models

The main goal of this model is to be suitable even if

the conditions change (move in the house, or change

of house …) and the model must to be portable from

one Alima to another. In order to do that, the model

must be adaptable on-line. To do that, we propose to

detect if the model varies from the reality, and to

perform a relearning only if needed.

0 1 2 3 4 Day

-0.15

-0.1

-0.05

0.05

0.1

0.15

0.2

0.25

0.3

Prediction

Error on pm

Figure 7: prediction error of pm.

In order to illustrate this, the preceding models

constructed with the data collected by airbox1 are

used with the data collected on airbox2.

The s-chart described part 3 is used in order to

determine if a relearning is needed. The size of the

samples is fixed to 240 minutes and so each sample

contains 240 patterns. Figure 8 presents the s-chart

obtained for the pm model used with data collected

by airbox2.

This figure shows that, as awaited, the model is

not accurate for the first sample of 240 data. So a

relearning occurs on these 240 first data. This

relearning allows to fit the model to these new

condition and the model accuracy is satisfactory

until the sample 25. For this sample, the value of the

standard deviation is slightly outside the bounds and

a second relearning is needed. So, for the 15 days of

the experiments, only 2 relearning are needed to

PredictionModelAdaptationThankstoControlChartMonitoring-ApplicationtoPollutantsPrediction

177

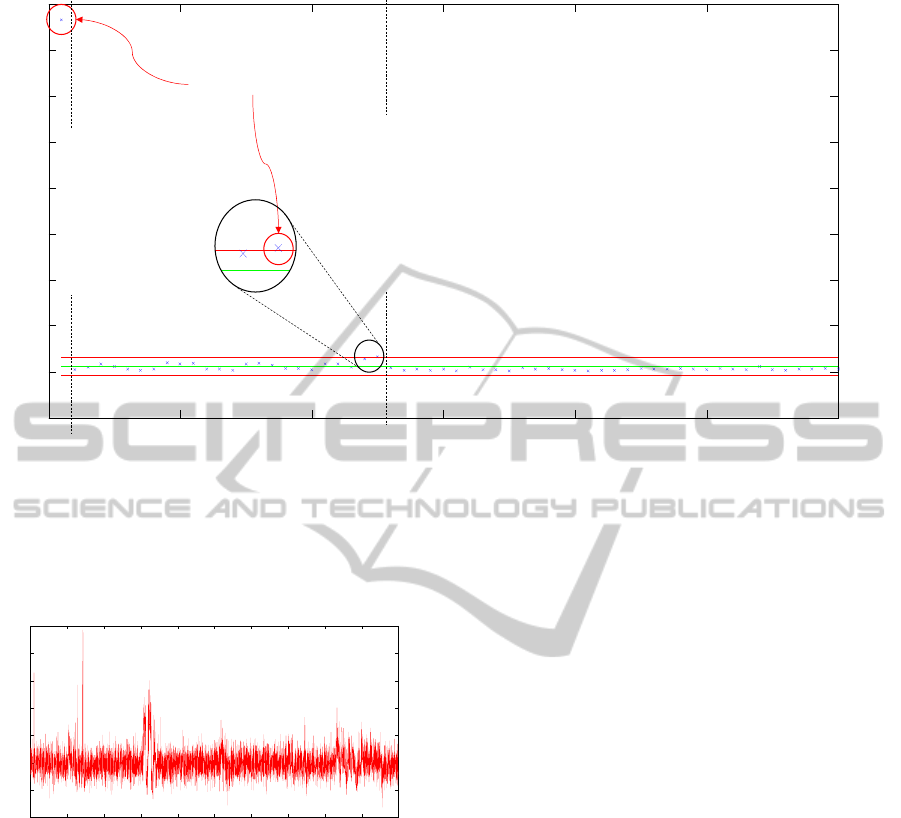
0 10 20 30 40 50 sam

les

-200

200

400

600

800

1000

1200

1400

S-chart

UCL

LCL

Relearning needed

Relearning executed

Figure 8: S-chart: monitoring of model accuracy.

maintain a good accuracy of the model.

Figure 9 presents the prediction error for the pm

pollutant. This figure shows that this strategy allows

maintaining an accurate model even when the

conditions change.

0 1 2 3 4 Day

-0.2

-0.1

0.1

0.2

0.3

0.4

Prediction

Error on pm

Figure 9: prediction error of pm for airbox2.

6 CONCLUSIONS

This paper presents a new on-line monitoring

strategy conserving the prediction model accuracy.

This strategy is based on the use of a control chart to

determine if a relearning is needed or not to adapt

the model to an evolution of the reality. This

approach is tested on a prediction model related to

pollutants levels. The results show that neural

networks are able to predict the evolution of

pollutants. Moreover, the proposed monitoring

strategy allows adapting quickly the considered

model to new conditions and, in the same time, to

limit the number of relearning needed. In future

works, this approach will be compared with on-line

learning on both accuracy and computational time.

ACKNOWLEDGEMENTS

The authors thanks the society Anaximen for their

active financial and scientific support for this work.

REFERENCES

Alima, http://getalima.com, 2013.

Cybenko, G., 1989. Approximation by superposition of a

sigmoidal function. Math. Control Systems Signals, 2,

4, 303-314.

Du, L., Ke, Y., Su, S., 2012. The Embedded Quality

Control System of Product Manufacturing, Advanced

Materials Research, 459, 510-513.

Engelbrecht, A.P., 2001. A new pruning heuristic based on

variance analysis of sensitivity information. IEEE

transactions on Neural Networks, 1386-1399

Funahashi, K., 1989. On the approximate realization of

continuous mapping by neural networks. Neural

Networks, 2, 183-192.

Han, H.G., Qiao, J.F., 2013. A structure optimisation

algorithm for feedforward neural network

construction. Neurocomputing, 99, 347-357.

Heskes, T., Wiegerinck, W., 1996. A theoretical

comparison of batch-mode, online, cyclic, and almost-

cyclic learning. IEEE Transactions on Neural

Networks, 7, 919-925.

Jones, A.P, 1999. Indoor air quality and health.

Atmospheric Environment, 33, 28, 4535-4564.

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

178

Liang, N.Y., Huang, G.B., Saratchandran, P., Sundarajan,

N., 2006. A fast and accurate online sequential

learning algorithm for feedforward networks. IEEE

Transactions on Neural Networks, 17, 1411-1423.

Ma, L., Khorasani, K., 2004. New training strategies for

constructive neural networks with application to

regression problems. Neural Network, 589-609.

Maroni, M., Seifert, B., Lindvall, T., 1995. Indoor Air

Quality – a Comprehensive Reference Book. Elsevier,

Amsterdam.

Nakama, T., 2009. Theoretical analysis of batch and on-

line training for gradient descent learning in neural

networks. Neurocomputing, 73, 151-159.

Nguyen, D., Widrow, B., 1990. Improving the learning

speed of 2-layer neural networks by choosing initial

values of the adaptative weights. Proc. of the Int. Joint

Conference on Neural Networks IJCNN'90, 3, 21-26.

NIST/SEMATECH, 2012. e-Handbook of Statistical

Methods, http://www.itl.nist.gov/div898/handbook/.

Setiono, R., Leow, W.K., 2000. Pruned neural networks

for regression. 6

Pacific RIM Int. Conf. on Artificial

Intelligence PRICAI’00, Melbourne, Australia, 500-

509

Shewhart, W.A., 1931. Economic Control of Quality of

Manufactured Product, Van Nostrand Reinhold

Company, Inc.: Princeton, NJ.

Spengler, J. D., Sexton, K., 1983. Indoor air pollution: a

public health perspective. Science, 221, 9-17.

Tague, N.R., 2004. The Quality Toolbox, 2nd Edition,

ASQ Quality Press, http://asq.org/learn-about-

quality/data-collection-analysis-

tools/overview/control-chart.html.

Thomas, P., Bloch, G., 1997. Initialization of one hidden

layer feedforward neural networks for non-linear

system identification. 15

IMACS World Congress on

Scientific Computation, Modelling and Applied

Mathematics WC'97, 4, 295-300.

Thomas, P., Bloch, G., Sirou, F., Eustache, V., 1999.

Neural modeling of an induction furnace using robust

learning criteria. Journal of Integrated Computer

Aided Engineering, 6, 1, 5-23.

Thomas, P., Suhner, M.C., Thomas, A., 2013. Variance

Sensitivity Analysis of Parameters for Pruning of a

Multilayer Perceptron: Application to a Sawmill

Supply Chain Simulation Model. Advances in

Artificial Neural Systems, Article ID 284570,

http://dx.doi.org/10.1155/2013/284570

Walsh, P.J., Dudney, C.S., Copenhaver, E.D., 1987.

Indoor air quality, ISBM 0-8493-5015-8.

PredictionModelAdaptationThankstoControlChartMonitoring-ApplicationtoPollutantsPrediction

179