Graph-based Kernel Representation of Videos for Traditional Dance
Recognition
Christina Chrysouli, Vasileios Gavriilidis and Anastasios Tefas
Department of Informatics, Aristotle University of Thessaloniki, University Campus 54124, Thessaloniki, Greece
Keywords:
Activity Learning, Random Walk Kernel, Support Vector Machines, Feature Extraction.
Abstract:
In this paper, we propose a novel graph-based kernel method in order to construct histograms for a bag of
words approach, by using similarity measures, applied in activity recognition problems. Bag of words is the
most popular framework for performing classification on video data. This framework, however, is an orderless
collection of features. We propose a better way to encode action in videos, via altering the histograms. The
creation of such histograms is performed based on kernel methods, inspired from graph theory, computed with
no great additional computational cost. Moreover, when using the proposed algorithm to construct the his-
tograms, a richer representation of videos is attained. Experiments on folk dances recognition were conducted
based on our proposed method, by comparing histograms extracted from a typical bag-of-words framework
against histograms of the proposed method, which provided promising results on this challenging task.
1 INTRODUCTION
Activity recognition, let alone dance recognition, is
one of the most challenging and active research ar-
eas in computer vision, which deals with the iden-
tification of human activities captured in video. In
recent years, this problem has drawn a lot of atten-
tion because of the wide variety of potential appli-
cations, including video surveillance (Li et al., 2011;
Niu et al., 2004) and video annotation (Robertson and
Reid, 2006). A detailed survey of human activity
recognition is presented in (Turaga et al., 2008).
Activity recognition from videos impose a huge
load of calculation because of the dimensionality of
the data. Thus, most of the algorithms use a prepro-
cessing step, in order to extract features. Among the
state-of-the art approaches is global spatio-temporal
templates, such as motion history (Bobick and Davis,
2001), and bag-of-words (BoW) representations. In
BoW representation, the “codewords” can be com-
puted in two different ways: statically for each frame
(Kl¨aser et al., 2008) or from trajectories (Wu et al.,
2011). Dense trajectories (Wang et al., 2011; Wang
and Schmid, 2013) have been widely used in prac-
tice (Peng et al., 2013; Kapsouras et al., 2013; Raptis
et al., 2012) in order to extract semantic information
about the video.
In activity recognition, extracting features from
a video is only the beginning. The goal is to at-
tach a label to each video clip in a dataset, using a
classifier (Iosifidis et al., 2013a). The way that the
video clip is represented as features plays an impor-
tant role to the performance of the classifier. A lot of
work has been done on the BoW framework in im-
age categorisation tasks. BoW methods, which repre-
sent an image as an orderless collection of local fea-
tures, have demonstrated impressive levels of perfor-
mance (Willamowski et al., 2004; Zhang et al., 2007).
However, other works highlight the disadvantages of
the BoW approach, proposing to construct histograms
that better represent the dataset (Grauman and Dar-
rell, 2005; Lazebnik et al., 2006) or, even, alter the
way the codebook is calculated (Ravichandran et al.,
2013; Iosifidis et al., 2013b). We propose using a dif-
ferent method of assigning descriptors of a video to
“codewords” in the codebook, hence, resulting to dif-
ferent histograms as video representations. Moreover,
instead of using a dissimilarity measure, a Kernel ma-
trix, inspired from graph theory, has been employed.
Kernel methods have received increasing atten-
tion, particularly due to the popularity of the Sup-
port Vector Machines (SVM), as they provide a trans-
formation from linearity to non-linearity and can be
easily expressed in terms of dot products, using the
kernel trick (Sch¨olkopf and Smola, 2001). Graphs
provide a general sense of similarity between objects
(in our case video descriptors) that reflect the whole
structure of data. In information retrieval the notion of
195
Chrysouli C., Gavriilidis V. and Tefas A..
Graph-based Kernel Representation of Videos for Traditional Dance Recognition.
DOI: 10.5220/0005076101950202
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 195-202
ISBN: 978-989-758-054-3
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

replacing the BoW with a graph is not new (Rousseau
and Vazirgiannis, 2013), however, using a random
walk kernel in activity learning has never been pro-
posed before.
The novel contribution of this paper is threefold:
• A novel Graph of Words video representation is
proposed that goes beyond the standard BoW,
capturing the structure of the data by using a graph
of codewords and defining a p-step random walk
similarity on this graph, in order to estimate the
representation histograms.
• A novel methodical way to use p-step random
walk kernel matrices in the proposed framework
is described in detail.
• The proposed method has been applied on a
very challenging and not well-studied so far area,
the recognition of traditional dances, yielding
promising results compared to the standard BoW
method.
The remainder of this paper is organised as fol-
lows. In Section 2, the problem that we solve is stated
and some general aspects that concern the algorithm
are discussed. In Section 3, the proposed algorithm,
using a different approach of BoW, based on graphs,
is presented in detail. The experimental results of the
algorithm, on folk dance recognition, are described
in Section 4. Finally, in Section 5, conclusions are
drawn and future work is discussed.
2 PROBLEM STATEMENT
Activity recognition usually deals with the problem of
every day, simple actions recognition, such as walk-
ing, sitting, waving etc. In this paper, we have fo-
cused on dance recognition from videos, in particular
on Greek folk dances recognition, which can be con-
sidered much more challenging than generic activity
recognition. Activity recognition is a very active re-
search field but, due to the great diversity of dancing
styles as well as the wide variety of movements in-
volved in even a single dance performance, very little
research has been performed on dance recognition.
Feature trajectories are very popular and seem to
be efficient for representing videos, hence, in this pa-
per, improved dense trajectories have been employed
(Wang et al., 2011) in order to extract information
from the videos. The trajectories are acquired by
tracking densely sampled points from multiple spatial
scales, using optical flow information.
In more detail, a criterion is employed in order to
prune feature points in homogeneous areas. Such ar-
eas lack of any structure making it impossible to track
points onto them. Feature points are tracked for each
scale separately on a grid, by computing optical flow
for each frame. Median filter is then applied in the op-
tical flow, in order to track the next frame. Trajecto-
ries are formed by concatenating points of subsequent
frames. The shape of any trajectory can be expressed
as a sequence of displacement vectors, which are then
normalised according to their magnitudes.
Finally, a number of other descriptors are calcu-
lated, in particular histograms of oriented gradient
(HOG) (Dalal and Triggs, 2005), histograms of op-
tical flow (HOF) (Ikizler-Cinbis and Sclaroff, 2010)
and motion boundary histograms (MBH) (Dalal et al.,
2006), in order to encode more information about mo-
tion in videos, then, the final descriptor constitutes
from the concatenated descriptors. A space-time vol-
ume around the trajectory, which is further subdivided
into a smaller grid, is used in order to compute these
descriptors.
Usually, the high amount of the descriptors, de-
rived through this procedure, leads to a further pro-
cess, in order to use them for classification reasons.
The BoW approach is a common way to reduce the
number of the descriptors. The goal is to construct a
vocabulary, also called codebook, in which the most
representative features are defined as codewords.
The typical BoW framework can be summarised
as follows. First, the features need to be extracted
and described and then the codebook needs to be gen-
erated. The k-means algorithm is employed in order
to obtain the k most descriptive feature vectors, the
codewords, out of the training data. These k clus-
ter centroids can, then, be used as a discriminative
representation of the feature vectors. The Euclidean
distance is then used in order to map each training
feature vector to the closest cluster centroid. Next, a
histogram for every training feature vector is formed,
by calculating the frequency of appearance for every
cluster centroid. using the resulting distribution of
samples in descriptor space as a characterisation of
the whole dataset. This means that a codebook which
consists, for example, of 1000 codewords, produces
histograms of size 1000 as well. The same procedure
also applies for the extracted testing feature vectors,
in order to obtain the new representation for them as
well.
The BoW approach is an adaptable framework,
since it constitutes of steps that may be altered ac-
cording to the needs of any application. In this paper,
alternations have been made in order to accomplish
good classification results concerning video data.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
196

3 PROPOSED METHOD
One of the drawbacks of the previously published ap-
proaches is that the calculation of the histograms in
the BoW scheme is based on the distance between
descriptors and the codebook and, thus, this distance
plays an important role in classification. Usually, the
data that we need to handle are multidimensional.
On a high dimension, a simple distance measure, as
the one is used in a typical BoW framework, is not
enough to encode the geometry of the data.
In the proposed scheme, all the codewords of the
codebook are connected in a nearest neighbor graph
that also captures the structure (manifold) of the code-
words, thus, representing better the geometrical struc-
ture of the dataset. Moreover, the construction of the
graph gives us the ability to define similarity measures
on the graph, as the p-step random walk similarity we
propose, that represent better the similarity on nonlin-
ear manifolds. To the best of our knowledge, this is
the first paper that incorporates graph-based distances
in the popular BoW approach. Moreover, we propose
a methodical way to use kernel matrices applied on
BoW approach.
In order to create a better representation for the
descriptors in a video, a kernel matrix has been em-
ployed. Kernel matrices have proven to be extremely
powerful in many areas of machine learning. Two
of the most common choices for similarity matrices
are inner product and heat kernel; however, another
choice could be to use a kernel, based on graph the-
ory (Chung, 1996). The kernel, that is proposed in
this paper, is similar to a random walk kernel, which
was first proposed in (Szummer and Jaakkola, 2002),
and was later better defined as kernel matrix for semi–
supervised learning using cluster kernels (Chapelle
et al., 2002).
The proposed kernel matrix is created based on
the following property: if W represents the adjacency
matrix between nodes, where W(i, j) is defined as:
W(i, j) =

1, if i, j are connected
0, otherwise
(1)
then the ij–th element of the p–th power of adjacency
matrix, W
p
(i, j), gives the number of paths of length
p between nodes i and j. This notion can be applied
to either directed or undirected graphs and can also be
extended to weighted graphs, where W(i, j) ∈ [0, inf).
Extending the notion of BoW to graph–of–words
(GoW), we propose to treat descriptors and codebook,
denoted as d and C respectively, as nodes in a graph.
As we have already pointed out, by adopting this tech-
nique, we exploit the properties of graphs in order to
gain better geometrical representation of the data. Let
K denote a kernel matrix such as inner product or heat
kernel. Consequently, K consists of all the pairwise
similarities between descriptors and codebook, hence
K can be expressed in terms of sub-matrices as:
K =

S
C
S
T
Cd
S
Cd
S
d

, (2)
where:
• S
C
holds similarities between C and C.
• S
Cd
holds similarities between C and d.
• S
d
holds similarities between d and d.
We may, then, define the matrix that expresses simi-
larity paths of length p, as:
K
p
= KK. . . K
|
{z }
p times
. (3)
Note that it is straightforward to prove that K
p
is also
a kernel matrix.
One would be tempted to calculate equation (3),
but this would lead to computational intensive cal-
culations. Typically, the codebook is relatively small
(hundred or thousands of samples), whereas the num-
ber of the descriptors could be quite large (million
of samples). Since the descriptors are represented as
nodes in a graph, we may apply restrictions on simi-
larity paths, in order to avoid computationally inten-
sive calculations, (e.g. S
d
in (2) or matrix multipli-
cations in (3). In order to achieve that, only paths
that pass exclusivelythroughthe codebookexistin the
graph are allowed, whereas paths that pass through
the descriptors are excluded. Hence, we define an-
other matrix, the restriction matrix, K
R
which is cal-
culated the same way as K, but zeros are added to ev-
ery graph path that begins from the descriptors. Thus,
K
R
contains only elements that correspond to paths
that begin from codebook nodes. This restriction ma-
trix can be expressed as:
K
R
=

S
C
S
T
Cd
0 0

. (4)
We may now compute the p–th power of kernel ma-
trix as:
K
∗
=KK
p−1
R
=

S
C
S
T
Cd
S
Cd
S
d

S
C
S
T
Cd
0 0

p−1
=

S
C
S
T
Cd
S
Cd
S
d

S
p−1
C
S
p−2
C
S
T
Cd
0 0

=
"
S
p
C
S
p−1
C
S
T
Cd
S
Cd
S
p−1
C
S
Cd
S
p−2
C
S
T
Cd
#
(5)
Graph-basedKernelRepresentationofVideosforTraditionalDanceRecognition
197

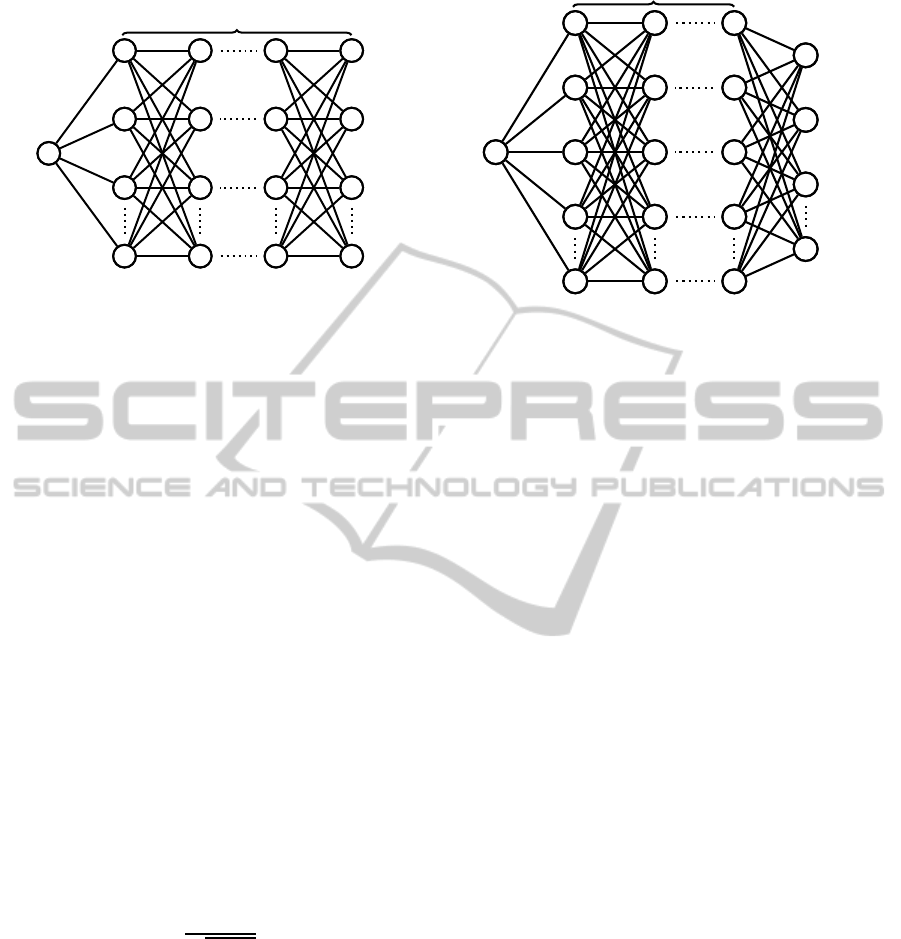
p−1
d
i
u
1
u
2
u
3
u
M
u
1
u
2
u
3
u
M
S
d
i
u
1
S
d
i
u
2
S
d
i
u
3
S
d
i
u
M
(a) Passing through one codebook C
M
p−2
d
i
υ
1
υ
2
υ
3
υ
4
S
d
i
υ
1
S
d
i
υ
2
S
d
i
υ
3
S
d
i
υ
4
S
d
i
υ
N
υ
N
u
M
u
1
u
2
u
3
(b) Passing through two codebooks C
N
, C
M
Figure 1: In both 1(a), 1(b), the following notation is used: d
i
is a single descriptor, C
M
, C
N
are two different codebooks
with M < N, u
1
, u
2
, ..., u
M
are the codewords of C
M
, υ
1
, υ
2
, ..., υ
N
are the codewords of C
N
and the edges are weighted
with similarity values between two nodes. In 1(a), the way that the similarity is calculated, between a descriptor d
i
and the
codebook C
M
is illustrated. In 1(b), the way that two codebooks can be used in order to enchance similarity is illustrated. In
more detail, the descriptor d
i
first passes through the C
N
codebook, creating similarity paths of length p− 2, and then passes
through the C
M
codebook.
The matrix S
Cd
S
p−1
C
, which expresses how de-
scriptors are connected through similarity paths of
length p with the codebook, is, in fact, the only ma-
trix that needs to be computed. Notice that descriptors
do not contribute to similarity paths, but only define
where do these similarity paths begin from. Power
iterations are involved only in the similarity matrices
between codebooks, making this method effectiveand
scalable. In addition, when p = 1, S
Cd
S
p−1
C
= S
Cd
,
which expresses the similarities between descriptors
and the codebook as if a simple kernel matrix was
used.
Elevating a matrix to a power produces relatively
large similarity values. In order to deal with that prob-
lem the kernel K is normalised as in (Graf and Borer,
2001) in order to take values in the interval [0, 1], us-
ing the following equation:
˜
K
∗
ij
=
K
∗
ij
q
K
∗
ii
K
∗
j j
. (6)
In terms of computational cost, the only difference
between the GoW framework and the typical BoW
framework is the power iterations of S
C
. Moreover,
the matrix S
C
can be substituted to its eigenvalue de-
composition S
C
= UDU
T
. Then S
p
C
may be easily
computed as S
p
C
= UD
p
U
T
. Although, except for the
submatrix S
Cd
S
p−1
C
, no other submatrices in (5) need
to be computed, we do need to calculate the diagonal
values of K
∗
, for the normalisation process.
3.1 Enhanced Version of Codebook
The size of the codebook is an important factor to ac-
tivity recognition. Generally the larger the codebook
the better the results. However, sometimes, a small
codebook is necessary, as it yields faster classification
results and is also space efficient. Thus, we need low
dimensional histograms that encode as much infor-
mation as possible. This enhancement is attained by
forcing the descriptors to pass through the large code-
book and end up to the small codebook, with lower
dimension representation, but carrying the informa-
tion of the large codebook. Overall, it is important to
have a compact but useful representation. Thereafter,
we also propose an even more sophisticated method
that makes use of two different codebooks, C
M
and
C
N
respectively, of different sizes, M and N, where
M < N. The new kernel K can be defined similarly as
in (2):
K =



S
C
N
S
T
C
MN
S
C
MN
S
C
M
 
S
T
dC
N
S
T
dC
M


S
dC
N
S
dC
M

S
d


, (7)
where:
• S
C
N
holds similarities between C
N
and C
N
.
• S
C
M
holds similarities between C
M
and C
M
.
• S
C
MN
holds similarities between C
N
and C
M
.
• S
dC
M
holds similarities between d and C
M
.
• S
dC
N
holds similarities between d and C
N
.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
198

In order to allow paths to pass only from the larger
codebook C
N
, zeros are inserted in the restriction ma-
trix as follows:
K
R
=



S
C
N
S
T
C
MN
0 0
 
S
T
dC
N
0


0 0

0


. (8)
The (p− 1)-th power of the restriction matrix can
now be computed as:
K
p−1
R
=



S
C
N
S
T
C
MN
0 0
 
S
T
dC
N
0


0 0

0


p−1
=



S
p−1
C
N
S
p−2
C
N
S
T
C
MN
0 0
 
S
p−2
C
N
S
T
dC
N
0


0 0

0


.
Finally the the p–th power of kernel matrix is
computed as:
K
∗
= KK
p−1
R
=




"
S
p
C
N
S
p−1
C
N
S
T
C
MN
S
C
MN
S
p−1
C
N
S
C
MN
S
p−2
C
N
S
T
C
MN
# "
S
p−1
C
N
S
T
dC
N
S
C
MN
S
p−2
C
N
S
T
dC
N
#
h
S
dC
N
S
p−1
C
N
S
dC
N
S
p−2
C
N
S
T
C
MN
i
S
dC
N
S
p−2
C
N
S
dC
N




.
(9)
The submatrix S
dC
N
S
p−2
C
N
S
T
C
MN
expresses how de-
scriptors are connected to the small codebook pass-
ing through similarity paths of the large codebook.
Again, the normalisation of the matrix is performed
using equation (6), but in this case only diagonal val-
ues of S
C
MN
S
p−2
C
N
S
T
C
MN
and S
dC
N
S
p−2
C
N
S
dC
N
need to be
calculated. Moreover, notice that, the kernel matrix
in the enchanced version of codebook, is meaningful
only if p ≥ 2. Using p = 2 implies one step from
the descriptors to the first codebook C
N
, and one step
from C
N
to the second codebook C
M
. p = 1 is not a
valid value for p, as we need at least two steps to go
from descriptors to the large codebook C
N
and then
to the small codebook C
M
. In Figure 1, the similar-
ity paths of the two different approaches for a single
descriptor are illustrated.
The advantage of the proposed method is that it
is generic and can be used in a wide diversity of
other problems, including image/scene classification,
or even dimensionality reduction, using graph embed-
ding approaches.
4 EXPERIMENTAL RESULTS
The originality of the proposed method, also comes
from the application that it has been applied on: tradi-
tional dance recognition. Generally, even though a lot
of work has been performed on activity recognition,
very little prior work has been done on recognition
of traditional dances. In order to evaluate the pro-
posed algorithm presented in Section 3, we have con-
ducted experiments on a Greek folk dances dataset.
In Greece, but also in every European countries, there
is a great diversity of traditional dances even within a
specific region. Many of the traditional dances have
similar steps, rhythm or tempo making the distinction
between them more challenging.
The dances that are performed in the videos in
the dataset, come from Western Macedonia region.
The initial dataset consists of 10 videos, in which
5 different traditional dances are performed: Lotzia,
Capetan Loukas, Ramna, Stankena and Zablitsena.
Each dance is performed twice by different profes-
sional dancing groups and an example of the dataset
is illustrated in Figure 2. Then, 5 videos are used
as a training set, whereas the rest are used as a test-
ing set. The resolution of the videos was 160×120,
while the duration varied from 1.5 minutes to 3.5 min-
utes, which was enough to complete a full sequence
of steps more than 10 times in each performance.
The final dataset is formed by temporally seg-
menting each of the videos into smaller clips of 100
frames duration. The new clips, that are obtained
through this procedure, overlap with each other by 80
frames, concerning a single video at a time. The num-
ber of the produced clips are presented in Table 1 for
both training videos and testing videos, resulting to
the final training and testing set of 497 and 516 short
clips respectively.
Table 1: Dataset.
Train Test
Lotzia 78 102
Capetan Loukas 113 107
Ramna 110 110
Stankena 95 106
Zablitsena 101 91
Total 497 516
First, the extraction of the descriptors is performed
on every frame, on both training and testing video
clips of the dataset. The features, that are extracted for
this purpose, are dense trajectories, HOG and HOF
descriptors and motion boundary histograms calcu-
lated separately for horizontal (MBHx) and vertical
(MBHy) dimensions. The final descriptor, for every
frame, consists of the concatenation of the aforemen-
tioned descriptors.
Due to time and space efficiency reasons, only
a small amount of the descriptors, from every 10
frames, are chosen in order to calculate the code-
words. The codebook is then created with the aid of
Graph-basedKernelRepresentationofVideosforTraditionalDanceRecognition
199

Figure 2: Greek folk dance “Zablitsena”, performed indoor by professional dance groups with different costumes.
the k-means algorithm, with k centers meaning that
k codewords exist in the codebook. In our exper-
iments, two different codebooks were created, con-
taining k = 100 and k = 1000 codewords. It is im-
portant to point out that the codebooks were created
once and the same two codebooks (of 100 and 1000
codewords) were used for all of our experiments, for
comparison reasons.
The videos differ from each other in terms of
background, number of people performing a dance
and the costumes that they wear (Figure 2). The
background does not play an important role when ex-
tracting features, as precautions have been taken to
eliminate points with no or little structure (Section 2).
On the other hand, different costumes seem to affect
the classification results. Moreover, dance recogni-
tion has many particularities, even in a single dance
performance. For example, there are many songs
that change from slow to fast rhythm and vice versa,
which greatly affects the tempo of the dance. Thus,
the problem of recognising dances, even when only 5
classes are involved, is very challenging.
In the proposed method, classification is per-
formed using a multilabel SVM classifier with χ
2
ker-
nel. The evaluation of the parameters was performed
using a grid search of 5-fold cross validation. In more
detail, we have trained with exponentiallygrowing se-
quences of C ∈

2
−10
, ..., 2
20

in order to derive the
parameter C that best classifies the currently evalu-
ated data. After calculating the best parameter for the
training set, the entire dataset is trained once again
to obtain a new refined model of the SVM. The new
model could then be applied on the testing set, in or-
der to obtain labels for its data.
In this paper, we aim to test if the proposed
method performs better than a typical bag-of-words
framework. Thus, for comparison reasons, experi-
ments have also been conducted for the typical BoW
approach, using the same parameters as in the GoW
framework, in order to train and test with the same
dataset. The results of the typical BoW framework
as well as the results of the proposed method, as de-
scribed in Section 3, are presented in Table 2.
The histograms obtained after the BoW or the
GoW approach have the same length as the number
of the codewords in the codebook. In Table 2 “BoW
100” and “BoW 1000” indicate the results of the clas-
sification, which were obtained from the typical BoW
framework, for codebook sizes of 100 and 1000 code-
words respectively. Likewise, “GoW 100” and “GoW
1000” indicate the results of the proposed method (5),
where heat kernel similarity was used (2), in order
to obtain a new representation of the histograms of
100 and 1000 length, respectively. Lastly, “GoW 100
through 1000” indicates the results of the proposed
method, where new histograms of size 100 are also
calculated, but which have already passed through the
codebook of 1000 codewords, as described in Sec-
tion 3.1. “Similarity kernel” refers to the heat ker-
nel similarity matrix that was employed in the pro-
posed method, while “γ” refers to the parameter of
the heat kernel similarity matrix and “Graph power”
refers to the power on which the similarity matrix was
elevated.
We observe, from the first two lines of Table
2, that using the typical BoW approach, with either
100 or 1000 codewords, the results remain almost
the same, with almost no improvement in classifi-
cation results when going from 100 to 1000 code-
words. This means that although we extractlarger his-
tograms, the extra information that is encoded in them
is quite small. The proposed method, using similar-
ity paths of length p, in order to produce histograms,
performs much better than the typical BoW frame-
work that is compared to. In the case of 1000 code-
words the proposed method seems to outperform all
the others, achieving a classification score of 46.9%,
for SVM parameter C = 2
4
, on the testing dataset.
Considering the complexity of the problem as well
as the difficulty of representing a video of hundreds
of frames as a feature of 1000 or less features the
scores achieved using the proposed method is defi-
nitely a great accomplishment. Although the classi-
fication performance when using histograms of size
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
200

Table 2: Classification results on the Greek folk dances dataset, using a SVM with χ
2
kernel.
Similarity
γ
Graph Classification
kernel power performance
BoW 100 (typical) - - - 37.02
BoW 1000 (typical) - - - 38.57
GoW 100
(proposed)
heat
kernel
5
2 35.85
3 37.02
4 37.79
5 39.53
6 38.95
GoW 1000
(proposed)
heat
kernel
5
2 38.57
3 46.9
4 44.57
5 44.19
6 45.16
GoW 100
through
1000
(proposed)
heat
kernel
5
2 32.95
3 34.5
4 27.71
5 41.67
6 45.35
100, that have passed through the codebook of 1000
centers, is slightly lower, the results are encouraging
as we have managed to encode almost the same in-
formation in histograms of a much lower size, thus,
achieving space efficiency.
5 CONCLUSIONS
A novel algorithm has been presented that makes
use of a graph-of-words approach in order to achieve
good classification results, with the aid of the random
walk kernel. Moreover, the new representation of his-
tograms that was used seems to improve the classifi-
cation results in comparison to the typical BoW ap-
proach.
It is important to remark that the algorithm is ap-
plied to a difficult problem, the folk dances recogni-
tion, due to the great variety of figures, even within
the same dance, as well as because of the similari-
ties between different dances (e.g. most Greek folk
dances are performed in a circle). The results on this
challenging area are promising but also provethat tra-
ditional dance recognition is a very difficult task.
In the future, we plan to improve the proposed
graph-based kernel representation of videos for ex-
ample by using a larger codebook in order to encode
more information of the video sequences, or even by
enhancing the codebook with better or/and more de-
scriptors.
ACKNOWLEDGEMENTS
This research has been co–financed by the European
Union (European Social Fund - ESF) and Greek na-
tional funds through the Operation Program “Educa-
tion and Lifelong Learning” of the National Strate-
gic Reference Framework (NSRF) - Research Fund-
ing Program: THALIS–UOA–ERASITECHNIS MIS
375435.
REFERENCES
Bobick, A. F. and Davis, J. W. (2001). The recognition
of human movement using temporal templates. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 23(3):257–267.
Chapelle, O., Weston, J., and Sch¨olkopf, B. (2002). Cluster
kernels for semi-supervised learning. In Advances in
Neural Information Processing Systems, page 15.
Chung, F. R. K. (1996). Spectral Graph Theory (CBMS
Regional Conference Series in Mathematics, No. 92).
American Mathematical Society.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In Computer Vision and
Pattern Recognition, 2005. CVPR 2005. IEEE Com-
puter Society Conference on, volume 1, pages 886–
893. IEEE.
Dalal, N., Triggs, B., and Schmid, C. (2006). Human de-
tection using oriented histograms of flow and appear-
ance. In Computer Vision–ECCV 2006, pages 428–
441. Springer.
Graph-basedKernelRepresentationofVideosforTraditionalDanceRecognition
201

Graf, A. B. A. and Borer, S. (2001). Normalization in sup-
port vector machines. In in Proc. DAGM 2001 Pattern
Recognition, pages 277–282. SpringerVerlag.
Grauman, K. and Darrell, T. (2005). The pyramid match
kernel: discriminative classification with sets of image
features. In Computer Vision, 2005. ICCV 2005. Tenth
IEEE International Conference on, volume 2, pages
1458–1465 Vol. 2.
Ikizler-Cinbis, N. and Sclaroff, S. (2010). Object, scene
and actions: Combining multiple features for human
action recognition. In Computer Vision–ECCV 2010,
pages 494–507. Springer.
Iosifidis, A., Tefas, A., and Pitas, I. (2013a). Dy-
namic action recognition based on dynemes and ex-
treme learning machine. Pattern Recognition Letters,
34(15):1890–1898.
Iosifidis, A., Tefas, A., and Pitas, I. (2013b). Multi-
dimensional sequence classification based on fuzzy
distances and discriminant analysis. Knowledge
and Data Engineering, IEEE Transactions on,
25(11):2564–2575.
Kapsouras, I., Karanikolos, S., Nikolaidis, N., and Tefas,
A. (2013). Feature comparison and feature fusion for
traditional dances recognition. In Engineering Appli-
cations of Neural Networks, pages 172–181. Springer.
Kl¨aser, A., Marszalek, M., and Schmid, C. (2008). A spatio-
temporal descriptor based on 3d-gradients. In BMVC.
British Machine Vision Association.
Lazebnik, S., Schmid, C., and Ponce, J. (2006). Beyond
bags of features: Spatial pyramid matching for rec-
ognizing natural scene categories. In Proceedings
of the 2006 IEEE Computer Society Conference on
Computer Vision and Pattern Recognition - Volume 2,
CVPR ’06, pages 2169–2178, Washington, DC, USA.
IEEE Computer Society.
Li, B., Ayazoglu, M., Mao, T., Camps, O. I., and Sznaier, M.
(2011). Activity recognition using dynamic subspace
angles. In Computer Vision and Pattern Recogni-
tion (CVPR), 2011 IEEE Conference on, pages 3193–
3200. IEEE.
Niu, W., Long, J., Han, D., and Wang, Y.-F. (2004). Human
activity detection and recognition for video surveil-
lance. In Multimedia and Expo, 2004. ICME’04. 2004
IEEE International Conference on, volume 1, pages
719–722. IEEE.
Peng, X., Wu, X., Peng, Q., Qi, X., Qiao, Y., and Liu, Y.
(2013). Exploring dense trajectory feature and en-
coding methods for human interaction recognition. In
Proceedings of the Fifth International Conference on
Internet Multimedia Computing and Service, pages
23–27. ACM.
Raptis, M., Kokkinos, I., and Soatto, S. (2012). Dis-
covering discriminative action parts from mid-level
video representations. In Computer Vision and Pat-
tern Recognition (CVPR), 2012 IEEE Conference on,
pages 1242–1249. IEEE.
Ravichandran, A., Chaudhry, R., and Vidal, R. (2013). Cat-
egorizing dynamic textures using a bag of dynamical
systems. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 35(2):342–353.
Robertson, N. and Reid, I. (2006). A general method for
human activity recognition in video. Computer Vision
and Image Understanding, 104(2):232–248.
Rousseau, F. and Vazirgiannis, M. (2013). Graph-of-word
and tw-idf: New approach to ad hoc ir. In Proceedings
of the 22nd ACM International Conference on Infor-
mation & Knowledge Management, CIKM ’13, pages
59–68, New York, USA. ACM.
Sch¨olkopf, B. and Smola, A. J. (2001). Learning with Ker-
nels: Support Vector Machines, Regularization, Opti-
mization, and Beyond. MIT Press, Cambridge, MA,
USA.
Szummer, M. and Jaakkola, T. (2002). Partially labeled
classification with markov random walks. In Ad-
vances in Neural Information Processing Systems,
pages 945–952. MIT Press.
Turaga, P., Chellappa, R., Subrahmanian, V. S., and Udrea,
O. (2008). Machine recognition of human activities:
A survey. Circuits and Systems for Video Technology,
IEEE Transactions on, 18(11):1473–1488.
Wang, H., Kl¨aser, A., Schmid, C., and Liu, C.-L. (2011).
Action Recognition by Dense Trajectories. In IEEE
Conference on Computer Vision & Pattern Recog-
nition, pages 3169–3176, Colorado Springs, United
States.
Wang, H. and Schmid, C. (2013). Action recognition with
improved trajectories. In IEEE International Confer-
ence on Computer Vision, Sydney, Australia.
Willamowski, J., Arregui, D., Csurka, G., Dance, C. R., and
Fan, L. (2004). Categorizing nine visual classes using
local appearance descriptors. In ICPR Workshop on
Learning for Adaptable Visual Systems.
Wu, S., Oreifej, O., and Shah, M. (2011). Action recogni-
tion in videos acquired by a moving camera using mo-
tion decomposition of lagrangian particle trajectories.
In Computer Vision (ICCV), 2011 IEEE International
Conference on, pages 1419–1426. IEEE.
Zhang, J., Lazebnik, S., and Schmid, C. (2007). Local fea-
tures and kernels for classification of texture and ob-
ject categories: a comprehensive study. International
Journal of Computer Vision, 73:2007.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
202