
Occupational Diseases Risk Prediction by Cluster Analysis and
Genetic Optimization
Antonio di Noia
1
, Paolo Montanari
2
and Antonello Rizzi
1
1
Department of Information Engineering, Electronics and Telecommunications, University of Rome "La Sapienza"
Via Eudossiana 18, Rome, Italy
2
Research Department, National Institute for Insurance against Accidents at Work (INAIL), Rome, Italy
Keywords: Occupational Diseases, Risk Prediction, Computational Intelligence, Cluster Analysis, Genetic Algorithm.
Abstract: This paper faces the health risk prediction problem in workplaces through computational intelligence
techniques applied to a set of data collected from the Italian national system of epidemiological
surveillance. The goal is to create a tool that can be used by occupational physicians in monitoring visits, as
it performs a risk assessment for workers of contracting some particular occupational diseases. The
proposed algorithm, based on a clustering technique is applied to a database containing data on occupational
diseases collected by the Local Health Authority (ASL) as part of the Surveillance National System. A
genetic algorithm is in charge to optimize the classification model. First results are encouraging and suggest
interesting research tasks for further systems’ development.
1 INTRODUCTION
Employee health care is gaining attention by both
private and public companies, as well by OHS
(Occupational Health and Safety) organizations
worldwide. In fact, part of the public costs dedicated
to healthcare can be reduced by monitoring and
controlling workplaces hazards. In this scenario, a
potentially useful challenge is to apply data mining
and knowledge discovery techniques on related
databases, extracting useful information to perform
occupational hazard assessment by health risk
classification methods. To this aim, several studies
show that the application of computational
intelligence techniques can lead to reveal the
existence of structures in the data difficult to detect
with other approaches. For example, in (Chinmoi et
al, 2012) have been developed a decision support
system for employee healthcare, while in (Razan et
al, 2010) have been applied clustering techniques to
medical data to predict the likelihood of diseases. In
(Zhaohui Huang Daoheng Yu Jianye Zhao, 2000)
artificial neural networks have been applied by
Zhaohui Huang Daoheng Yu Jianye Zhao in
occupational diseases incidence forecast.
This work shows the first results of a study for
the application of techniques of data analysis and
computational intelligence to an occupational
diseases database. The goal is the development of a
tool for predicting the likelihood of contracting a
disease as a function of some characteristics of both
the worker and the working environment. The
database contains data collected over a decade by
the Local Health Authority of the Italian Lombardy
region. The problem of identifying possible causes
of risk hazards in work places has been formulated
as a classification one. To this aim, a suited
classification system has been developed, relying on
cluster analysis as the core procedure of the machine
learning engine. In order to automatically determine
both the parameters of the dissimilarity measure
between patterns and to identify the best structural
complexity of the classification model (number of
clusters), a genetic algorithm has been employed to
synthetize the best performing classifier.
2 DATA PROCESSING
The data set has been extracted from the archive of
occupational diseases collected by the Local Health
Authority (ASL) as part of the National System of
Surveillance "MalProf", managed by the National
Institute for Insurance against Accidents at Work
(INAIL). The data set contains records for each
pathology collected from ASL, storing information
68
Di Noia A., Montanari P. and Rizzi A..
Occupational Diseases Risk Prediction by Cluster Analysis and Genetic Optimization.
DOI: 10.5220/0005077800680075
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 68-75
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

on registry of the worker, on his work history and
his pathology. For each worker more than one record
may be present in the archive (a single record for
each pathology).
In order to develop and test the whole prediction
system, a first data set with controlled cardinality
has been defined by considering only the cases of
the Lombardy Italian region recorded in the period
1999-2009. Moreover, in order to simplify pattern’s
structure, only records related to workers with a
single pathology and an occupational history
consisting of a single working activity have been
considered. This data set has been cleaned removing
ambiguous situations, inconsistent or missing data.
This first preprocessing step yielded a data set of
3427 records as shown in Table 1; as a further
filtering, the data set records of diseases below the
5% rate were not considered, yielding the final data
set of 2722 records, covering about 80% of cases,
highlighted with colored background in Table 1.
Table 1: Records distribution for pathology.
Disease
N
. of
records
Cumulative
N
. of records
Freq.
Cumulative
Freq.
Hearing loss 1493 1493 0.436 0.436
Spinal diseases 334 1827 0.097 0.533
musculoskeletal
disorders
(excluding
spinal diseases)
288 2115 0.084 0.617
Tumors of the
pleura and
peritoneum
232 2347 0.068 0.685
Carpal tunnel
syndrome
199 2546 0.058 0.743
Skin diseases 176 2722 0.051 0.794
Disorders of the
ear (except
hearing loss)
137 2859 0.040 0.834
Mental illness 98 2957 0.029 0.863
Diseases of the
respiratory
system
76 3033 0.022 0.885
Other diseases 394 3427 0.115 1
The final available data set has been partitioned
into three subsets by random stratification: the
training set (50% of the total number of available
patterns, denoted with S
TR
), the validation set (25%,
S
VAL
) and the test set (the remaining 25%, S
TEST
).
Table 2 shows the distribution of diseases and their
labels as integer numbers codes. The similarity
between the subjects was evaluated through a
distance function based on 6 features (Table 3), both
numerical and categorical, identified by a
preliminary analysis of data and knowledge in the
field.
Table 2: Pathologies in descending order of frequency.
Pathologies Training set
Validation set
1 - Hearing loss
747
54.89%
373
54.85%
2 - Spinal diseases
167
12.27%
83
12.21%
3 - Musculoskeletal
disorders
144
10.58%
72
10.59%
4 - Tumors of the pleura
and peritoneum
116
8.52%
58
8.53%
5 - Carpal tunnel
99
7.27%
50
7.35%
6 - Skin diseases
88
6.47%
44
6.47%
Total
1361
100%
680
100%
Table 3: Features.
Code Meaning Data Type
x1
Age of the worker at the time
of disease assessment (years)
numerical
x2
Duration of the working
period (months)
numerical
x3
Age at the beginning of the
working period (years)
numerical
x4 Gender categorical
x5
Profession carried out by the
worker
categorical
x6 Company's economic activity categorical
The profession of the worker is coded through a
pair of characters based on the Italian version of the
classification system ISCO. The International
Standard Classification of Occupations (ISCO) is a
tool for organizing jobs into a clearly defined set of
groups according to the tasks and duties undertaken
in the job. The economic activity of the company is
coded by a pair of characters based on the Italian
version of the NACE classification system. NACE
(Nomenclature des Activités Économiques dans la
Communauté Européenne) is a European industry
standard classification system similar in function to
Standard Industry Classification (SIC) and North
American Industry Classification System (NAICS)
for classifying business activities.
3 THE PROPOSED ALGORITHM
In order to design an algorithm able to evaluate the
probability of contracting an occupational disease as
OccupationalDiseasesRiskPredictionbyClusterAnalysisandGeneticOptimization
69

a function of some characteristic of the worker, his
work history and his work environment, the risk
prediction problem has been reformulated as a
classification problem. The basic classification
system is a clustering based one, which is trained in
a supervised fashion, by discovering clusters of
labelled patterns in S
TR
. Once the clusters are
identified, the classification rule is defined by
considering, within each cluster, the class label with
higher frequency. A test pattern is classified by
assigning the class label according to the cluster
representative label having minimum dissimilarity
value. The algorithm was coded in C++ language.
3.1 Basic Algorithm
The core procedure during the synthesis of a
classification model consists in clustering S
TR
by the
well –known k-means algorithm. To this aim, an ad
hoc dissimilarity measure δ between patterns was
defined as a convex linear combination of inner
dissimilarity measures δ
i
between homologues
features:
N
i
ii
vupvu
1
,),(
(1)
where N is the number of the features (6 in our case)
and
1,0;
ii
pp
is the relative weight of the i-
th feature.
The δ
i
(u,v) distance between patterns u and v
relative to the i-th feature have been defined
differently on the basis of the considered feature
type, which can be continuous or categorical
(discrete nominal) values:
for age (in years) and the duration of the activity
(in months), δ
i
is the Euclidean distance
normalized in the unitary interval [0,1];
for gender and economic activity of the
company, in the case of concordance δ
i
= 0,
otherwise δ
i
= 1 (simple match);
for the job of the individual, in the case of
concordance of both characters δ
i
= 0, in the case
of concordance of the first character only δ
i
= ½,
otherwise δ
i
= 1.
The overall classification system has been
designed to automatically determine the weights p
i
of the dissimilarity measure (1) and the optimal
number of clusters k, in order to maximize the
classification accuracy:
Sx
Kxx
h
S
accuracyf ),(
1
1
(2)
where:
S is the labelled pattern set on which is computed the
accuracy;
Ω = {hearing loss, spinal diseases, musculoskeletal
disorders, tumors of the pleura and peritoneum,
carpal tunnel syndrome, skin diseases} is the
considered label set;
x
is the pathology of worker
Sx
(ground
true class label);
Kx
is the label assigned by the classification
model to x;
h(ω
x
, ω
Kx
) = 1 if ω
x
= ω
Kx
;
h(ω
x
, ω
Kx
) = 0 if ω
x
≠ ω
Kx
;
In order to perform this optimization task, we
have developed a suited implementation of a genetic
algorithm. The generic individual of the population
subject to evolution by genetic operators is formed
of two data structures (sections) for a total of 7
parameters to be optimized:
1. a vector of 6 real numbers between 0 and 1,
corresponding to the weights associated with
the features in the distance function δ;
2. an integer between 2 and a maximum value
fixed in the system parameters, corresponding
to the number of clusters to be used for the
clustering of the training set.
From one generation to the next, each individual
in the GA is evaluated by a fitness function defined
as the accuracy (2), computed on S
VAL
. The selection
is simulated using a roulette wheel operator. The
crossover and mutation affect the entire individual,
formed by six weights and the number of clusters.
The individuals of the initial population of the
GA are created as random samples. For each
individual, a clustering procedure with k-means is
performed on the training set with weights fixed in
the first section of the individual’s genetic code and
setting the number of clusters as the integer number
stored in the second section. Once obtained a
partition of the S
TR
, each cluster is assigned with a
unique label, defined as the most frequent pathology
in the cluster. Successively the fitness is computed
as the classification accuracy on the validation set,
according to (2).
Reproduction, crossover and mutation are
applied to the individuals of the GA to evolve the
population, until a stop criterion based on a
maximum number of generations is met. The
algorithm is summarized in Table 4.
The distribution of pathologies in the data set
shows that class labels (diseases) are not well
balanced, and this could distort the values of fitness
by giving excessive importance to the most frequent
pathology. Therefore, it is introduced a variant of
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
70

fitness function aiming to equally weight all
misclassifications, regardless of their number. The
new fitness (equation (3)) is given by the weighted
accuracy, i.e. the mean value of the percentages of
correct answers for each pathology. Tests were
performed with both fitness and the results have
been compared.
Sx
Kxxweighted
h
S
accuracyf ),(
11
2
(3)
where:
S
ω
is the subset of S of all elements associated with
pathology
(
SS
).
Table 4: Summary of the basic algorithm.
Input parameters:
- Maximum number of clusters: Kmax
- Number of population’s individuals in the GA: Pop
- Number of generations of GA: nGeneration.
1. Reading data from S
TR
and S
VAL.
2. Initialization (Generation = 0).
For j = 1 to Pop
o Random assignment of weights p
i
of the 6
features and of the value K ≤ Kmax.
o Clustering of the elements of S
TR
into K
clusters using the distance function (equation 3)
with the parameters encoded in the individual j
o Evaluation of the fitness of individual j with
the function
in equation 1
3. For q = 1 to nGeneration
o Application of elitism.
o Repeat
Selection of individuals of the old population
by roulette wheel operator.
Crossover between pairs of the selected
individuals.
Mutation with a low probability on each
element.
Clustering of S
TR
in K clusters using the
distance function (1) with the parameters
encoded in the individual.
Evaluation of the fitness function (2) on S
VAL
Until complete new generation
3.2 A Second Variant of the Algorithm
The basic algorithm leads to the formation of
clusters containing more than one disease. The label
associated with the cluster coincides with the most
frequent pathology in it. This procedure cannot
assure the presence of at least one cluster for each
class. To make sure that all the pathologies are
represented in the final classification model, a
second version of the proposed classification system
has been designed.
For this purpose, the training set S
TR
has been
partitioned into six subsets, one for pathology. The
new algorithm runs six cluster analyses in parallel,
one for each of the 6 subsets of S
TR
. As a
consequence, each cluster will contain patterns
associated with a unique class label and will
consequently be directly labeled. The union of the
six sets of labeled clusters originated will be directly
employed for the classification model definition.
The generic individual of the population of the
GA has been adapted to the new algorithm; in
particular, the second part of the individual no
longer contains a single integer, but 6 integers, each
representing the number of clusters to use in the 6
cluster analysis performed in parallel on each subset
of the training set (one for each class label). The
initialization step of the first generation of the GA is
similar to the basic algorithm. As for the previous
version, we considered both the fitness functions f
1
and f
2
computed on S
VAL
(Equations (2) and (3)) for
individual fitness evaluation.
4 RESULTS
All experiments were conducted using the GA by
evolving a population of 100 individuals for 50
generations, fixing to 20 the maximum number of
clusters. All performances reported in the following
tables are computed on the test set. Table 5 shows
the classification results as a confusion matrix, in the
case of the basic algorithm and using equation (2) as
fitness. All correct guesses are located in the
diagonal (highlighted in gray) of the table, so it is
easy to inspect visually the table for errors, as they
will be represented by any non-zero value outside
the main diagonal.
For each of the 6 diseases, further views can be
extracted from the Confusion matrix in the
Confusion table’s schema (see Table 6). Given the
content of the dataset, formed only by workers
affected by pathologies, for each disease are
considered as healthy the workers not affected from
that pathology. The columns “Positive to test” and
“Negative to test” of Confusion tables contain the
number of workers that the algorithm predicts
respectively as sick (i.e. affected by the disease in
question) or healthy (i.e. affected by other diseases).
The rows “Actual true” and “Actual false” contain
the number of those who actually are, respectively,
sick and healthy. For example, the two confusion
tables (table 7a and 7b) shown below summarize the
cases “1-hearing loss” and “4-
tumours of the pleura
and peritoneum”.
OccupationalDiseasesRiskPredictionbyClusterAnalysisandGeneticOptimization
71
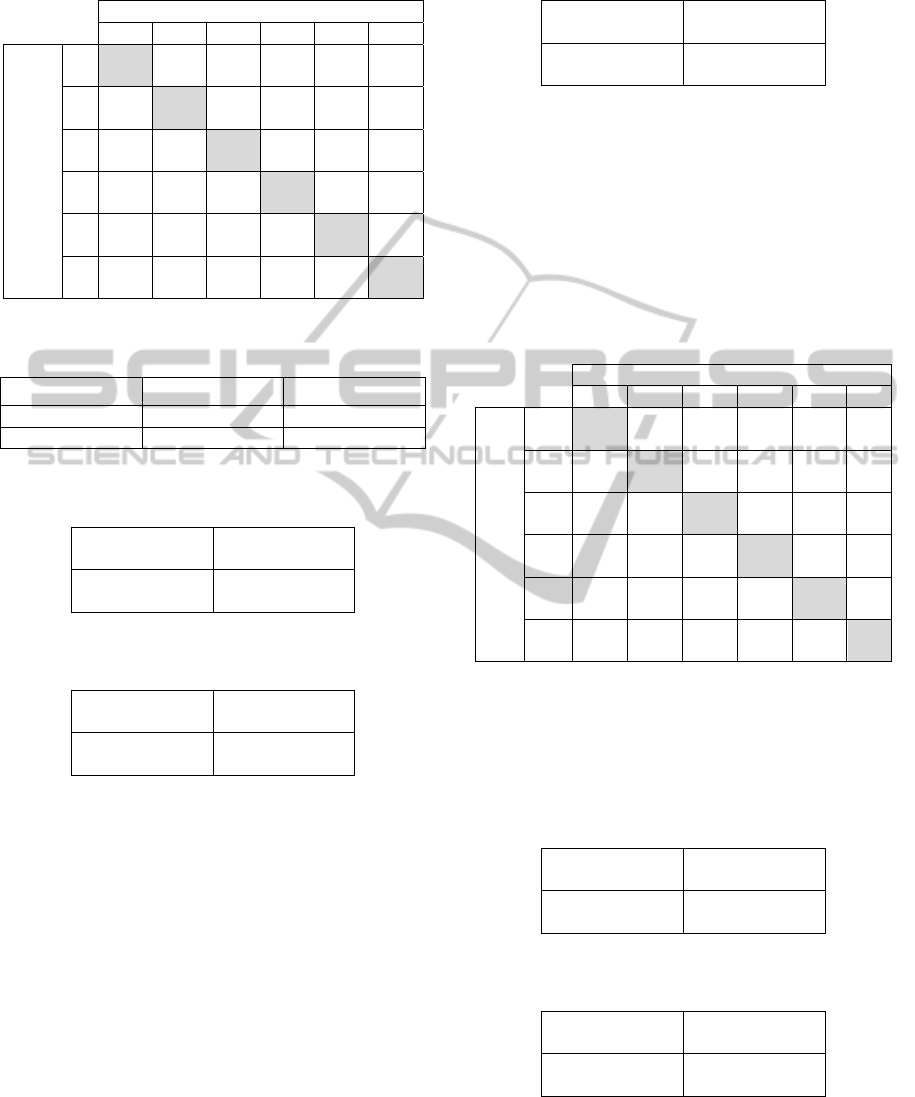
Table 5: Confusion matrix for basic algorithm with f
1
. In
brackets normalized values as percentage.
Predicted class
1 2 3 4 5 6
Actual
class
1
351
(94.1)
5
(1.3)
0
(0.0)
7
(1.9)
9
(2.4)
1
(0.3)
2
45
(54.2)
36
(43.4)
0
(0.0)
0
(0.0)
1
(1.2)
1
(1.2)
3
32
(44.4)
20
(27.8)
0
(0.0)
0
(0.0)
16
(22.2)
4
(5.6)
4
18
(31.0)
8
(13.8)
0
(0.0)
32
(55.2)
0
(0.0)
0
(0.0)
5
9
(18.0)
16
(32.0)
0
(0.0)
1
(2.0)
23
(46.0)
1
(2.0)
6
20
(45.5)
7
(15.9)
0
(0.0)
0
(0.0)
4
(9.1)
13
(29.5)
Table 6: Confusion table’s schema for the evaluation of
the predictive ability of a test.
Positive to test Negative to test
Actual true True positives False negatives
Actual false False positives True negatives
Table 7a: Confusion table for pathology “1-hearing loss” –
basic algorithm using f
1.
351
True positives
22
False negatives
124
False positives
183
True negatives
Table 7b: Confusion table for pathology “4- tumors of the
pleura and peritoneum” – basic algorithm using f
1
.
32
True positives
26
False negatives
8
False positives
614
True negatives
The confusion tables allow more detailed
analysis than mere proportion of correct guesses
(accuracy). Accuracy is not a reliable metric for the
real performance of a classifier, because it will yield
misleading results if the data set is unbalanced. For
example, if there were 95 sick and only 5 healthy in
the data set, the classifier could easily be biased into
classifying all the samples as sick. The overall
accuracy would be 95%, but in practice the classifier
would have a 100% recognition rate for the sick
class and a 0% recognition rate for the wealthy class.
For these reasons, we reported the overall confusion
table (see table 8) containing the average values for
all classes.
Table 8: Confusion table with average values - basic
algorithm with f
1
.
75.8
True positives
37.5
False negatives
37.5
False positives
529.2
True negatives
The results of the second experiment, based on
the basic algorithm using the fitness f
2
, are shown in
table 9. The number of clusters of the best individual
of the last generation is 20, of which 13 are labeled
as "1 - hearing loss, 2 as "2 - spinal diseases", 1 as
"3 - musculoskeletal disorders", 2 as " 4 - tumors of
the pleura and peritoneum", 1 as "5 - carpal tunnel"
and 1 as " 6 - skin diseases."
Table 9: Confusion matrix for basic algorithm with f
2
. In
brackets normalized values as percentage.
Predicted class
1 2 3 4 5 6
Actual
class
1
338
(90.6)
7
(1.9)
7
(1.9)
15
(4.0)
6
(1.6)
0
(0.0)
2
36
(43.4)
35
(42.2)
4
(4.8)
0
(0.0)
7
(8.4)
1
(1.2)
3
32
(44.4)
12
(16.7)
14
(19.4)
0
(0.0)
13
(18.1)
1
(1.4)
4
18
(31.0)
1
(1.7)
7
(12.1)
32
(55.2)
0
(0.0)
0
(0.0)
5
8
(16.0)
6
(12.0)
12
(24.0)
2
(4.0)
21
(42.0)
1
(2.0)
6
21
(47.7)
3
(6.8)
0
(0.0)
0
(0.0)
8
(18.2)
12
(27.3)
Similarly to the previous case, the two confusion
tables (table 10a and 10b) summarize the cases “1 –
hearing loss” and “4 – tumours of the pleura and
peritoneum”.
Table 10a: Confusion table for pathology “1 – hearing
loss” – basic algorithm using f
2
.
338
True positives
35
False negatives
115
False positives
192
True negatives
Table 10b: Confusion table for pathology “4 – tumors of
the pleura and peritoneum” – basic algorithm using f
2
.
32
True positives
26
False negatives
17
False positives
605
True negatives
The final confusion table containing the average
values for all classes concerning the second
experiment is shown in Table 11.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
72

Table 11: Confusion table with average values - basic
algorithm with f
2
.
75.3
True positives
38.0
False negatives
38.0
False positives
528.7
True negatives
In the third experiment, based on the proposed
variant of the algorithm using the fitness f
1
, the best
individual of the last generation shows an overall
classification accuracy equal to 62%. The total
number of clusters was 36, with the following class
distribution: 20 are labelled as "1 - hearing loss", 6
as "2 – spinal diseases," 2 as "3 - musculoskeletal
disorders", 4 as "4 - tumors of the pleura and
peritoneum", 2 as "5 - carpal tunnel" and 2 as "6 -
diseases of the skin". In table 12 are summarized the
data of the six tables of confusion (one for disease).
Each column represents the confusion table for the
indicated disease in the column header. The final
table of confusion with average values is shown in
Table 13.
Table 12: Summarized data of the confusion tables -
variant of the algorithm with f
1
.
Pathology
1 2 3 4 5 6
True
positives
312 42 12 35 1 19
False
positives
127 59 19 15 20 19
False
negatives
61 41 60 23 49 25
True
negatives
180 538 589 607 610 617
Table 13: Confusion table with average values – variant of
the algorithm with f
1
.
70.2
True positives
43.2
False negatives
43.2
False positives
523.5
True negatives
In the fourth experiment, based on the variant of
the algorithm with the fitness f
2
, we obtained the
53% of correct classification in correspondence of
the best individual of the last generation. The total
number of clusters was 71, with the following class
distribution: 18 are labeled as "1 - hearing loss", 10
as "2 - spinal diseases", 7 as "3 - musculoskeletal
disorders", 11 as "4 - tumors of the pleura and
peritoneum", 15 as "5 - carpal tunnel", 10 as "6 -
skin diseases". The results for this experiment are
shown in Table 14 and in Table 15
Table 14: Summarized performances of the confusion
tables - variant of the algorithm with f
2
.
Pathology
1 2 3 4 5 6
True
positives
210 44 17 35 30 25
False
positives
48 61 45 30 89 46
False
negatives
163 39 55 23 20 19
True
negatives
259 536 563 592 541 590
Table 15: Confusion table with average values – variant of
the algorithm with f
2
.
60.2
True positives
53.2
False negatives
53.2
False positives
513.5
True negatives
Table 16: Chromosome of GAs.
Basic
Algorithm
using f
1
Basic
Algorithm
using f
2
Variant of
Algorithm
using f
1
Variant of
Algorithm
using f
2
Feature x1 1.000 1.000 0.870 0.660
Feature x2 0.041 0.134 0.894 0.709
Feature x3 0.078 0.346 0.569 1.000
Feature x4 0.592 0.519 1.000 0.196
Feature x5 0.189 0.220 0.280 0.726
Feature x6 0.265 0.076 0.096 0.141
N. cluster 10 20 – –
N. cluster
pathology 1
– – 20 18
N. cluster
pathology 2
– – 6 10
N. cluster
pathology 3
– – 2 7
N. cluster
pathology 4
– – 4 11
N. cluster
pathology 5
– – 2 15
N. cluster
pathology 6
– – 2 10
The Table 16 shows the genetic code of the best
individual produced by the GA for each experiment.
The first six parameters encode the weight of the
features (normalized values) and the other
parameters encode the clusters num
ber.
Another significant tool for performance
analysis, commonly used in the evaluation of
diagnostic tests, consists in the use of sensitivity and
specificity. Let us consider a study evaluating a new
test that screens people for a disease. The test
outcome can be positive (predicting that the person
is affected by the considered disease) or negative
OccupationalDiseasesRiskPredictionbyClusterAnalysisandGeneticOptimization
73

(predicting that the person is healthy). The test
results for each subject may or may not match the
subject's actual status. In that setting:
True positive: Sick people correctly
diagnosed as sick
False positive: Healthy people incorrectly
identified as sick
True negative: Healthy people correctly
identified as healthy
False negative: Sick people incorrectly
identified as healthy
The four outcomes can be expressed in a 2×2
confusion table, as in Table 17a. In table 17b are
defined the indicators used in diagnostic tests.
Table 17a: Confusion table.
Condition
positive
Condition
negative
Test
positive
True
positive
False
positive
Test
negative
False
negative
True
negative
Table 17b: Diagnostic Tests indicators.
Sensitivity = True positive / Σ Condition positive
Specificity = True negative / Σ Condition negative
Positive predictive value = True positive / Σ Test positive
N
egative predictive value = True negative / Σ Test neg.
In Table 18 are briefly described the diagnostic
test's indicators, using the average values calculated
on all pathologies. Table 19 summarizes the results
of 11 runs, with different initial seeds for the random
number generator, using the variant of algorithm
with f
2
. For both negative and positive predictive
values are reported the average performance,
standard deviation, minimum and maximum values,
for each disease and for the totality of the
pathologies.
Table 18: Diagnostic test’s indicators – average values.
Basic
Algorithm
using f
1
Basic
Algorithm
using f
2
Variant of
Algorithm
using f
1
Variant of
Algorithm
using f
2
Sensitivity 0.447 0.461 0.427 0.517
Specificity 0.905 0.907 0.895 0.901
Negative
predictive
value
0.929 0.923 0.906 0.892
Positive
predictive
value
0.503 0.574 0.460 0.442
Table 19: Negative and positive predictive values by
pathology resulting from a pool of 11 runs (variant of
Algorithm using f
2
).
Pathology 1 2 3 4 5 6 All
Patterns 373 83 72 58 50 44 680
Negative
predictive
value
Average 0,58 0,94 0,90 0,97 0,97 0,97 0,90
St. dev. 0,02 0,01 0,01 0,01 0,01 0,00 0,01
Min 0,54 0,92 0,90 0,96 0,96 0,96 0,89
Max 0,61 0,94 0,91 0,98 0,98 0,98 0,91
Positive
predictive
value
Average 0,82 0,38 0,26 0,48 0,28 0,28 0,50
St. dev. 0,01 0,03 0,05 0,09 0,03 0,04 0,03
Min 0,81 0,34 0,21 0,40 0,22 0,23 0,44
Max 0,85 0,43 0,35 0,67 0,34 0,35 0,53
In Tables 20 and 21 are shown the diagnostic
test’s indicators relative, respectively, to the
"hearing loss" and to the "tumors of the pleura and
peritoneum".
Table 20: Indicators relative to “1 – hearing loss”.
Basic
Algorithm
using f
1
Basic
Algorithm
using f
2
Variant of
Algorithm
using f
1
Variant of
Algorithm
using f
2
Sensitivity 0.941 0.906 0.836 0.563
Specificity 0.596 0.625 0.586 0.844
Negative
predictive
value
0.893 0.846 0.747 0.614
Positive
predictive
value
0.739 0.746 0.711 0.814
Table 21: Indicators relative to “4 - tumors of the pleura
and peritoneum”.
Basic
Algorithm
using f
1
Basic
Algorithm
using f
2
Variant of
Algorithm
using f
1
Variant of
Algorithm
using f
2
Sensitivity 0.552 0.552 0.603 0.603
Specificity 0.987 0.973 0.976 0.952
Negative
predictive
value
0.959 0.959 0.963 0.963
Positive
predictive
value
0.800 0.653 0.700 0.538
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
74

5 CONCLUSIONS
The first experiment (basic algorithm using f
1
)
shows that the sensitivity has a very high value
(0.941) for the group “hearing losses” (larger group),
and an average value equal to 0.447. The pathology
“3 - musculoskeletal disorders” was never predicted
by the algorithm. The specificity presents a value
close to 0.6 for the group “hearing loss” and an
average value greater than 0.9. These first results
show that function f
1
privileges the most frequent
pathology. In the second experiment (basic
algorithm using f
2
), the sensitivity no longer has null
values. The average sensitivity is equal to 0.461,
value slightly better than the previous case. The
specificity has values similar to the ones in the
previous experiment. The third experiment (variant
of the basic algorithm using f
1
) shows performance
values in general slightly worse compared to the
basic algorithm. However, there is an improvement
for the sensitivity of some pathologies. The fourth
experiment (variant of the basic algorithm using f
2
)
shows that the use of f
2
compared to f
1
has led to an
improvement of the average sensitivity of almost a
decimal point. Regarding the specificity, for all
pathologies the values are always greater than 0.84,
with an average value of 0.901.
The comparison of the average values of the
indicators (Table 18) shows how the second
algorithm with f
2
present the highest sensitivity.
Regarding the specificity and the predictive value of
the negative outcome of the test, we have
substantially similar behaviours for the four
experiments. As concerns positive predictive value,
the basic algorithm with f
2
has provided the best
results. The high values, close to unity, for
specificity and negative predictive value are
encouraging. However, the variant of the algorithm,
while not showing results appreciably better than the
basic algorithm, has better performance by reducing
the execution time to a third compared to the basic
version, because clustering procedures are run on
smaller sets. Thus, for the final commitment of the
system, which has to deal with a much larger
database, the second version should be preferred,
considering also that its performances are very close
to the ones obtained with the basic algorithm. In
particular, as shown by standard deviations in table
19, performances are stable over multiple runs,
assuring a good reliability to the results. Moreover,
the negative predictive value can be considered
sufficient to be used in a suited automatic screening
procedure, designed to reduce costs in performing
clinical trials on all the interested workers, since a
negative classification for a given worker is
sufficient to reliably ascertain his health status. Note
that in general for the groups “hearing loss” (the
largest group) and “tumors of the pleura and
peritoneum” (more severe disease) the results are
better than for other diseases, including the
sensitivity and the positive predictive value.
The examination of the weights of the features
(Table 16) shows different values for the different
algorithms. In all the experiments, only the
economic activity of the company seems less
important than the other features, so it might be
interesting to define a different set of features,
replacing the economic activity.
REFERENCES
A. K. Jane, R. C. Dubes, 1988. Algorithms for Clustering
Data, Prentice-Hall. Englewood Cliffs.
Alexandr A. Savinov, 1999. Mining Possibilistic Set-
Valued Rules by Generating Prime Disjunctions. In
PKDD'99, 3rd European Conference on Principles
and Practice of Knowledge Discovery in Databases.
Vol. 1704 Springer (1999), p. 536-541.
Chinmoy Mukherjee, Komal Gupta, Rajarathnam
Nallusamy, 2012. A Decision Support System for
Employee Healthcare. In Third International
Conference on Services in Emerging Markets.
Kumara Sastry, David Goldberg, Graham Kendall, 2005.
Genetic Algorithms. In Search Methodologies,
Springer US.
Razan Paul, Abu Sayed Md. Latiful Hoque, 2010.
Clustering Medical Data to Predict the Likelihood of
Diseases, IEEE - Digital Information Management
(ICDIM), Fifth International Conference.
Zhaohui Huang Daoheng Yu Jianye Zhao, 2000.
Application of Neural Networks with Linear and
Nonlinear Weights in Occupational Disease Incidence
forecast. In Circuits and systems. IEEE APCCAS
2000.
OccupationalDiseasesRiskPredictionbyClusterAnalysisandGeneticOptimization
75
