
Implementing a Software Cache for Genetic Programming
Algorithms for Reducing Execution Time
Savvas Karatsiolis and Christos N. Schizas
Department of Computer Science,University of Cyprus , 1 University Avenue, 2109 Nicosia, Cyprus
Keywords: Genetic Programming, Cache, Cache Invalidation.
Abstract: A cache holding reusable computations that are carried out during the execution of a genetic algorithm is
implemented and maintained in order to improve the performance of the genetic algorithm itself. The main
idea is that the operational genome is actually consisting of small computational blocks that tend to be
interchanged and reused several times before they complete (or not) their lifecycle. By computing these
blocks once and keeping them in memory for future possible reuse, the algorithm is allowed to run up to
fifty times faster according experimental results maintaining a general case execution time reduction of four
times. The consistency of the cache is maintained through simple rules that validate entries in a very straight
forward manner during the genetic operations of cross over and mutation.
1 INTRODUCTION
Evolutionary algorithms comprise a powerful class
of optimization techniques but do not scale very well
to large problems. This fact limits their usability and
consequently makes them inappropriate for difficult
online problems and really large datasets. Any
techniques that reduce the execution time of
evolutionary algorithms can be very useful and
greatly contribute to the popularity of the specific
algorithms in solving problems that demand huge
amounts of processing resources. This paper
discusses the implementation of a cache to a generic
genetic programming algorithm but there is no
reason why a similar technique could not be
implemented in other sub categories of the
evolutionary algorithms arsenal provided that the
right modifications are undertaken. Evolutionary
algorithms usually spend most if their execution
time on evaluating a candidate solution (an
individual of the undertaken population) and come
up with a numeric fitness value. For genetic
programming this translates into performing a great
deal of computations that can be very time
consuming depending on the complexity of the
genetic operations used.
The most often used operations are the basic
algebraic computations of addition, subtraction,
multiplication, division the trigonometric operations
of sine, cosine, tangent the exponential operations of
power, natural logarithm the squashing operations of
the step, logistic and Gaussian functions and the
logic operators of the greater/less than decisions.
The genetic operations selection is left to the
intuition, prior knowledge and creativity of the
designer and can have a substantial influence on the
execution time of the search. It is obvious that some
operations like the exponential or the square root
function for example, demand much more cpu
cycles that the computation of a simple addition.
Having a large dataset comprising many fitting
examples means that the fitness evaluation function
must be repeated many times (once for each
example). Considering the number of calculations
represented by each individual candidate solution, it
is evident that getting rid of the burden of
recalculating the same genetic blocks that have been
crossed over by the algorithm or the same
chromosomes that are just slightly altered by
mutation can significantly reduce the execution time
of the algorithm.
The problem of reducing the execution time of
genetic programming algorithms has been
investigated by a number of researchers. Poli (2008)
very briefly discusses several ways in that direction
with the use of a caching mechanism being one of
them. Other ways besides caching may be the
hardwiring of the genetic programming algorithm
execution on really fast hardware like dedicated
259
Karatsiolis S. and Schizas C..
Implementing a Software Cache for Genetic Programming Algorithms for Reducing Execution Time.
DOI: 10.5220/0005081202590265
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 259-265
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

circuitry (FPGAs), running the code on fast
graphical processing units (GPUs) or using
distributed processing.
Evidence for the potential benefits of using a
speeding up cache is provided by Vie Ciesielski and
Xiang Li (2004) in their analysis of genetic
programming runs. Many successful and effective
implementations proposed previously suggest a
different or modified representation of the
algorithm's individuals. For example, Handley
(1994) proposed the representation of the candidate
solutions through Directed Acyclic Graphs (DAG)
in a way that identical sub trees are not duplicated
and their fitness function values are cached in order
to be reused when possible. Machado and Cardoso
(1999) on the other hand propose an implementation
in which the individuals are not represented as
independent trees but as a merged tree with no sub
tree repetitions. Other implementations preserve the
traditional tree representation but maintain a hash
table to detect a potential cache hit.
In this paper, the genetic programming cache
proposed does not modify the classical tree
representation and does not demand complex control
processes to maintain the cache validity. On the
contrary, a set of simple rules invalidate the cache
after the genetic operations of crossover and
mutation are applied. We believe that through its
simplistic and effective nature it provides significant
advantages in comparison to other implementations
with the most important being its execution time
reduction and the fact that it is fully detached from
the mechanisms of a normal implementation that
does not use a cache. This quality makes it easy to
add the caching process to existing software genetic
programming implementations.
Along with the advantages of sparing significant
processing time comes the burden of maintaining a
sane and valid cache that is synchronized with the
main genetic operations. Since the cache is
implemented in software these maintenance steps
must be coded into the algorithm itself. On top of
these problems, the extra required memory for
setting up a cache mechanism must be taken under
consideration. In the next sections it will be shown
that maintaining the cache is a really simple task
with negligible overhead and the extra memory area
can be restricted to a couple of gigabytes for
medium sized problems.
2 CACHE IMPLEMENTATION
After initializing the genetic programming algorithm
a great part of the genome building blocks
manipulated by the genetic operators of crossover
and mutation is used in its original form, it is
modified partially or it is slightly altered. This
property is exploited to avoid recalculating the
values of a great number of such blocks during each
generation. To be able to implement a genetic
programming cache, two fundamental operations
must be developed: the cache hit and the cache
invalidation mechanisms. Cache replacement is not
of great concern because in contrast to the classical
cache concept, the genetic programming cache does
not maintain the locality of reference property. On
the contrary, the cache hits of a specific gene
operation depend solely on the relative fitness of the
chromosome they belong to and much less on the
fitness of the neighbouring gene representations.
As in the classic cache implementation, a cache
hit event takes place when a previously stored block
of data (or instructions) is requested for processing.
In the case of the genetic programming algorithm
which uses a software cache, in order to detect a
cache hit event, it is necessary to build and maintain
a set of auxiliary tables besides the cache table itself.
These auxiliary tables will be holding the necessary
information to provide the desired functionality.
This information is comprised of the cache index
(pointer) for a specific stored calculation already
performed and available for fast access, the next
operation following the cached calculation from
where the evaluation of a candidate solution must
continue and a validity flag for each cache entry. For
every candidate solution in the undertaken
population corresponds a row in the cache index
table which in turn has as many columns as the
maximum allowed length of the chromosomes. Each
slot in such a row represents a possible cache entry
index for each gene (operation) of a specific
individual of the population. This index leads to the
location of the numerical result of the operation
currently being executed in the actual cache table. In
this way the calculation procedure is spared and the
result is retrieved in a single memory access instead
of going through intensive cpu computations.
Maintaining the next operation to execute (returning
gene) is important because the evaluation function
must resume its normal operation from that node
after a cache hit. The returning-gene table entry is
also important in order to invalidate a cache entry
after it gets invalidated by having a genetic
operation like crossover and mutation acted upon it.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
260

The cache tables may be allocated dynamically, on
demand, or statically for convenience and ease of
management. Since dynamic allocation in this
implementation does not provide significant
advantages, static allocation is preferred and used.
The auxiliary cache tables have a capacity equal to
the product of the population times the max
allowable size of the chromosomes. In this way,
each gene of a candidate solution may have its own
pointer to a cache entry accompanied with a
returning-gene offset inside the chromosome itself
and a validity flag which signals the usability of the
stored result. For example if a population consists of
N individuals and the maximum size of each
individual is M genes then the following auxiliary
tables could be used
Cashed Gene Offset table having a size of N x
M single precision floating numbers
Cached Gene returning-gene offset table having
a size of N x M short integers
Cached gene validility flag table having a size
of N x 1 Booleans
In practice genetic programming algorithms use
genes that represent constant values or input
variables that act as operands of the mathematical
operations. There is no meaning in caching these
genes since they are constant values and do not
represent an underlying processing task. As a matter
of fact in a sane execution of the algorithm a
constant value should never trigger a cache hit and
this fact can be embedded in the coding in order to
constantly check for execution sanity.
The actual cache table is a large table that holds
the numerical results of already performed
calculations in order to have them available for reuse
during the execution of the genetic programming
algorithm. Every candidate solution is applied and
evaluated for its performance (fitness) for a number
of cases (training examples). This implies that every
entry in the cache represents a calculation that will
be repeated for all training cases and will of course
have a different result for each case. For
convenience and faster recalls each offset of the
cache forms a frame that holds the results of the
evaluation for each training example. For obvious
reasons each frame of the cache has a size which is
equal to the number of the training cases. For
example if the cache of a problem that deals with K
training cases consists of L frame entries the cache
table has a size of L x K floating numbers. The most
important elements of the proposed caching
implementation have been already referenced and so
everything is put together in Figure 1 which shows
the cache mechanism for an example equation and
its tree representation.
Figure 1: The cache auxiliary tables and the genes’ tree
shown for an example program of an evolutionary
algorithm.
The genetic program evaluates the fitness
function of an individual by applying the gene-
expressed mathematical equation on all training
examples one after the other. This procedure implies
that a cache frame should be in an ascending order
which in turn means that a cache hit is detected only
when all fitness cases regarding a computation block
have been run exactly once for each of the training
cases. It could be possible to maintain a table
pointing to which fitness case the cache entries are
valid for a specific block but it is not necessary since
it’s impossible to have a cache hit before the fitness
function is run for all cases. The latter observation
reflects the nature of the fitness function in genetic
programming algorithms where all cases are
considered before deciding for the fitness value of
an individual. This concept influences the way the
cache entries are marked as valid by having the
Boolean flag set only when all training cases have
been considered in the fitness evaluation function. If
the Boolean flag of a cache frame is set before the
completion of all training cases then a false cache hit
will fire in the next case consideration since the
cache offset stores the computational values of a
gene for all training cases as described before. In
implementation terms, the cache gene validity flag is
ImplementingaSoftwareCacheforGeneticProgrammingAlgorithmsforReducingExecutionTime
261

set when the last training example has been
considered in the fitness function of the algorithm
and not anytime before.
Before moving on to the invalidation mechanism
of the cache some more details regarding the
implementation of the cache hit mechanics are
necessary from the software coding point of view.
When the genetic programming algorithm starts
computing the fitness of a solution, it processes each
gene one after the other. Before executing the
corresponding computation it checks for a valid
cache entry by evaluating the cache gene validity
flag. If the flag is set then the computation is spared
and the values for all training cases regarding the
specific gene are retrieved from the cache. The
location of the cache frame is found in the cache
index table in the location that corresponds to the
index of the solution being examined. Along with
the values of the training cases the algorithm
retrieves the next gene location in the solution that
needs to be examined next. From figure 1 assuming
that node (3) fires a cache hit, the returning-gene
information will point to node (5). The evaluation
function resumes its operation from node (5) whose
result may or may not be in the cache. If cache hit
does not occur then the evaluating function performs
its computations as normally. The cache offsets
stored in the gene-index table are just accenting
integers that keep incrementing until the allocated
cache memory space is exhausted. At that point
there are three replacement strategies that can be
used: the least recently used replacement (LRU), the
FIFO replacement and the genome simplification
process. The LRU requires to keep an aging variable
in memory that is reset every time a hit occurs while
the FIFO strategy just resets the cache allocation
index to its zero relative address and start storing
cache calculations from the beginning. The third and
more appealing strategy is more appropriate for
genetic programming cache implementations since it
flushes the cache and builds up an updated one
through the application of a computational
simplification process. Complex nested genetic
programs are replaced with shorter blocks that are
mathematically equivalent. This reduces the average
length of the population and thus accelerates the
search even more. The invalidation of the cache is
discussed in more details in the following
discussion. The pseudo code that should be added to
the original fitness function of a genetic
programming algorithm is trivial and is shown in
Figure 2.
function FitnessFunction_CACHED()
for all Individuals in the population
for all TrainingCases
Offset=0;
while Offset < length(Individual)
index= AUX_CACHE_INDEXES[Individual,Offset]
if(AUX_CACHE_VALID[index]==true) // HIT
result = CACHE[index,TrainingCase]
Offset=AUX_CACHE_RETURN[Individual,Offset]
else // No Cache hit
result = . . . . . // Normal computations
Offset = . . . . . .
AUX_CACHE_INDEXES[Individual,Offset] =
CurrentIndex
CACHE[CurrentIndex,TrainingCase]=result
AUX_CACHE_RETURN[Individual,Offset]= Offset
if TrainingCase == TRAINING_CASES_SIZE
AUX_CACHE_VALID[CurrentIndex++] = true
Figure 2: The pseudo code of the modified fitness function
that incorporates the genetic programming cache.
Besides the cache hit detection and data retrieval,
in order to have a functional and sane cache
mechanism, data invalidation must be enforced in a
way that guarantees genes' value entries
synchronization. Cached gene values are valid as
long as the genes do not undergo any modification
since their initial computation. In a genetic
algorithm the genes are altered through genetic
operations like crossover and mutation. This means
that when two parents produce an offspring or an
individual gets mutated then the cached values
corresponding to the involved individuals must be
checked for validity. Some cached values must be
invalidated while others are not influenced by the
way a specific genetic operation is performed. To
detect which cache entries are invalid after a genetic
operation and which are valid, the auxiliary cache
table holding the returning nodes must be used. The
cache invalidation is explained based on a two point
crossover scheme which is slightly more complex
than one point crossover. The concept can be easily
transferred to multi point crossover operations and is
very similar to the checks performed for invalidating
the mutation operation. As mentioned before, the
invalidation rule is very simple: when a cached gene
is altered, its cached value is invalidated. The gene
alteration is detected by comparing the gene's
returning node to the crossover point and if it is
smaller, then the entry is still valid. On the contrary,
if the gene's returning node is higher than the
crossover point then the cached value must be
invalidated since there is definitely gene alteration in
the cached gene. Figure 3 shows the procedure in
more detail. Cached genes and their range (starting
and ending gene offset) are shown in the parents'
chromosomes. The crossover points define the way
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
262

the genes of the two individuals are to be mixed up
to form an offspring. For the case of the two point
crossover, the first part of parent 1 from its start to
point cx1 is used in the offspring intact - part (a) -
and the part between cx1 and cx2 is replaced with
the genes that are placed between points cx3 and cx4
of parent 2, namely part (b). Offspring's genes after
part (b) are a copy of the last part of parent 1,
namely part (c).
Figure 3: A two point crossover implementation of cache
invalidation.
After a crossover is finished and an offspring is
generated, the cache invalidation mechanism
performs the following steps
1. Resets (clears) the cache indexing entries of the
offspring in the auxiliary cache table.
2. Copies all auxiliary cache index table entries
and their returning nodes of the first parent
that correspond to genes that reside between
the first gene of the individual and the
crossover point cx1 provided that the cache
returning-gene node is before the crossover
point.
3. Copies all auxiliary cache index table entries
and their returning nodes of the second parent
that correspond to genes that reside between
crossover point cx3 of the individual and the
crossover point cx4 provided that the cache
returning-gene node is before cx4.
4. Copies all auxiliary cache index table entries
of the first parent and their returning nodes
that correspond to genes that reside between
crossover point cx2 and the last gene of the
individual.
When copying any auxiliary cache indexing
entries the values are copied exactly as they are
while when copying auxiliary cache returning nodes
the values are translated to the relative indexing
scheme of the new offspring. This is required
because the number of the genes between cx1 and
cx2 is not necessarily equal to the length of the
region between points cx3 and cx4. Nevertheless,
performing the indexing translation is trivial. The
pseudo code of crossover invalidation is shown in
Figure 4 below.
Figure 4: The crossover invalidation process
corresponding to steps 1, 2, 3 and 4 as defined before.
Invalidating the individual after a mutation
operation is a very similar procedure. However, the
mutation process constructs a table holding the
indexes of the genes of an individual that have been
mutated. All cached genes' values residing between
two consecutive mutation points are copied to the
resulting individual's auxiliary cache data as long as
their returning gene value is located before the
second mutation point (last gene of the examined
range). This rational is again based on the fact that
gene alteration desynchronizes the cache entry that
is associated with this gene.
3 EXPERIMENTAL RESULTS
In order to examine the execution time savings of
the genetic algorithm implementation the three most
influential factors are considered: population size,
population's average solution length and genetic
operators' complexity. While the first two are self
explanatory, the third factor has to do with the
ImplementingaSoftwareCacheforGeneticProgrammingAlgorithmsforReducingExecutionTime
263

atomic execution complexity of each computation.
For example since an additive operator is much
faster than a square root operator, it is expected that
greater savings are to be experienced when the
genome consists of more complex operators
(exponentials, square roots, entropy computations
etc) than primitive ones (addition, subtraction,
multiplication, division). An admittedly loose metric
of this observation is used indicating the content
ratio of the initial population genome's complex
operators over primitive ones. Two such cases are
examined corresponding to 25% and 50% of
complex operators over simpler ones in the initial
population's solutions. The problem selected for
evaluation is the symbolic regression of the 8-
dimensional Griewank function. The generalized
Griewank equation is given by
The two dimensional plot of the Griewank function
is shown in Figure 5.
Figure 5: The 2-d Griewank function plot.
The algorithm is written in C# and executed
using both the non-cache and the cache flavour for
populations of 100, 200 and 500 individuals for one
thousand generations each time. During the
executions of the algorithm the total fitness function
running time of both flavours is calculated and their
ratio is estimated at the end of the 1000 generations.
The experimental results of solving a problem of
500 fitness cases with different configuration
parameters are shown in table 1. The results grouped
in the two categories defined by the operators'
complexity are presented in the graphs shown in
Figure 6 and Figure 7. Each graph corresponds to
the population size used during execution. It is
obvious that the larger the population size or the
more complex the operators set used during
execution, the bigger the savings in execution time
accomplished by the cache mechanism. It must be
noted that the cache size used for the execution of
the algorithm was 2 Giga Bytes and the results were
averaged over 5 runs of different regression
problems.
Table 1: The experimental results regarding the execution
savings for various configurations of the genetic
algorithm.
Exec Time Ratio (Cache / No cache)
Complex.
Ratio
Avg
Length
Population100 Population
200
Population
500
0.5
25 0.69 0.53 0.41
40 0
.
51 0
.
41 0
.
35
55 0
.
3
9
0
.
36 0
.
31
7
50
.
35 0
.
2
9
0
.
26
100 0
.
33 0
.
25 0
.
21
163 0
.
2
9
0
.
22 0
.
1
7
200 0
.
2
7
0
.
18 0
.
14
2
7
00
.
26 0
.
15 0
.
11
350 0
.
1
9
0
.
11 0
.
0
7
500 0
.
14 0
.
08 0
.
04
1
25 0
.
45 0
.
4 0
.
36
40 0
.
3
9
0
.
36 0
.
32
55 0
.
34 0
.
2
9
0
.
3
7
50
.
28 0
.
2
7
0
.
24
100 0
.
26 0
.
26 0
.
22
150 0
.
22 0
.
21 0
.
1
7
200 0
.
18 0
.
16 0
.
12
250 0
.
15 0
.
14 0
.
1
350 0
.
13 0
.
1 0
.
06
500 0
.
11 0
.
0
7
0
.
02
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
264
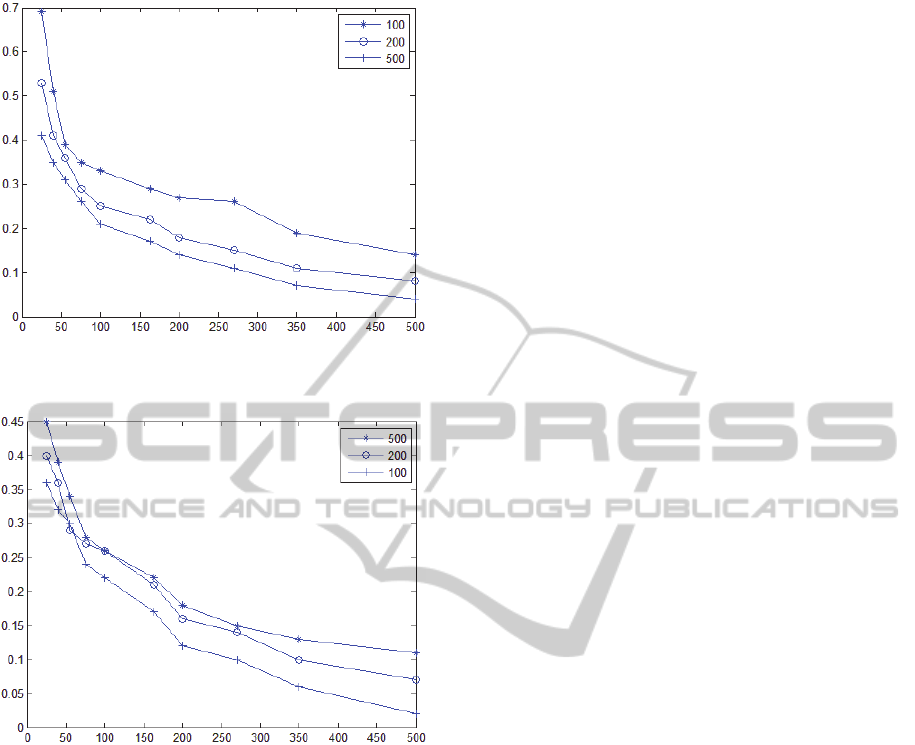
Figure 6: Experimental results for operators' complexity
ratio of 0.5 and various population sizes.
Figure 7: Experimental results for operators' complexity
ratio of 1 and various population sizes.
4 CONCLUSIONS
Using a cache significantly accelerates the execution
of a genetic programming algorithm, especially
when the solving process requires increased
operators' complexity and/or increased population
size during the search. It has been proved through
the experimental results that this improvement in
execution time can reach x50 times the normal (no
cache) execution. Furthermore, implementing the
cache does not require more than 2GBytes of
memory which is easily affordable.
REFERENCES
Koza, John R.. Genetic programming: on the
programming of computers by means of natural
selection. Cambridge, Mass.: MIT Press, 1992. Print.
Kinnear, Kenneth E.. Advances in genetic programming.
Cambridge, Mass.: MIT Press, 1994. Print.
Koza, John R.. Genetic programming III: darwinian
invention and problem solving. San Francisco:
Morgan Kaufmann, 1999. Print.
Poli, Riccardo, and W. B. Langdon. A field guide to
genetic programming. S.I.: [Lulu Press], lulu.com,
2008. Print.
Penousal Machado and Amilcar Cardoso. Speeding up
Genetic Programming. In Proceedings of the Second
International Symposium on Artificial Intelligence,
Adaptive Systems (CIMAF - 99), Havana, Cuba, 1999
V. Ciesielski and X. Li. Analysis of genetic programming
runs. In R. I. Mckay and S.-B. Cho, editors,
Proceedings of The Second Asian-Pacific Workshop
on Genetic Programming, Cairns, Australia, 6-7
December 2004
S. Handley. On the use of a directed acyclic graph to
represent a population of computer programs. In
Proceedings of the 1994 IEEE World Congress on
Computational Intelligence, 1994. IEEE Press
ImplementingaSoftwareCacheforGeneticProgrammingAlgorithmsforReducingExecutionTime
265
