
Fuzzy Control of a Sintering Plant
Marco Vannocci
1
, Valentina Colla
1
, Piero Pulito
2
, Michele Zagaria
2
, Vincenzo Di Mastromatteo
2
and Marco Saccone
2
1
PERCRO Laboratory, Scuola Superiore Sant’Anna, Via Alamanni 13D, San Giuliano Terme (Pisa), Italy
2
ILVA S.p.A., Strada Statale Appia Km 648, Taranto, Italy
Keywords:
Fuzzy Control, Expert Systems, Sinter Plant.
Abstract:
Within an integrated steelwork, the industrial priorities in the automation of the sinter plant comprise stable
production rate at the highest productivity level and classical control scheme may fail due to the complexity
of the sinter process. The paper describes an approach exploiting a fuzzy rule-based expert system to control
the charging gates of a sinter plant. Two different control strategies are presented and discussed within an
innovative advisory system that supports the plant operators in the choice of the most promising action to do
on each gate. Through the proposed approach the operators are supported by the system in the control of the
plant: through a suitable exploitation of real-time data, the system suggests the most promising action to do,
by reproducing the knowledge of the most expert operators. Thus, this approach can also be used to train new
technicians before involving them in the actual plant operations. The performance of the strategies and the
goodness of the system have been evaluated for long time in the sinter plant of one of the biggest integrated
steelworks in Europe, namely the ILVA Taranto Works in Italy.
1 INTRODUCTION
Within a steelwork, the sintering process is a central
operation in the production cycle: the treatment is
basically a high temperature process that starts from
raw materials mixture (such as fine iron ores) and
produces a particular form of agglomerate material
known as sinter, which is one of the material fed to the
blast furnace in order to produce the pig iron, which is
subsequently refined in the steel shop to produce the
liquid steel.
The sintering process is articulated into a series
of standard operations. A first preliminary task is the
acceptation and the storage of the iron-bearing raw
materials in the ore stockyard followed by the crash-
ing and the screening of these raw materials. Then,
the following phases which are more specific of the
sintering process can be pointed out: (I) raw mate-
rials are mixed together with water and then granu-
lated into a pseudo-particles in a rotary mixer drum
and then stocked in a feed hopper; (II) after the hop-
per, the moistened mix passes through the charging
gates and it is accumulated just before a leveler that
strips out the exceeding material; thus the moistened
mixture is charging as a layer onto continuously mov-
ing pallet-cars called “strand”; (III) after the ignition
of the material close to the charging zone, the burn-
ing process is propagated by chemical reaction thanks
to the air sucked through the strand by the so-called
wind boxes, that are depressurised air ducts mounted
below the strand; (IV) at the end of the strand the so-
lidified agglomerate is broken within a crusher and
cooled within a cooler strand; (V) finally the cooled
material is conveyed to a second crusher in order to
obtain a suitable size of the particles of the final sin-
ter.
The overall process must be controlled in order to
ensure that all the mix is burned just earlier than being
discharged into the crusher. The points at which the
flame front reaches the base of the strand are called
“burn-through points” (BTPs). Thus, among the aims
of the control process of the plant, two of them are
of considerable interest and can be summarized as
follows: to ensure that the BTPs are aligned in the
transversal direction of the strand and to ensure that
this alignment happens just earlier than the discharge.
As a matter of fact, a uniform flame front is guaran-
teed to the former condition while the latter one op-
timizes the production capacity of the plant. In fact
there is an evident waste of productivity of the plant
68
Vannocci M., Colla V., Pulito P., Zagaria M., Di Mastromatteo V. and Saccone M..
Fuzzy Control of a Sintering Plant.
DOI: 10.5220/0005082400680075
In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 68-75
ISBN: 978-989-758-053-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

if the BTPs occur too early compared to the end of the
process; analogously, the quality of the sinter lowers
if the burning process is not completed before the dis-
charge and this fact negatively affects the production
rate of the overall steel plant and the following pro-
duction stages.
Predictive capabilities have been used to develop
control schemes controlling the speed of the strand.
In (Kanjilal and Rose, 1986) the prediction of the
waste gas temperature is used to manipulate the strand
speed, while in (Hu and Rose, 1997) the same vari-
able is controlled using a process model identified
from the observed data. A different perspectiveis pre-
sented in (Arbeithuber et al., 1995), where the control
scheme tries to keep the temperature distribution at
the end of the plant on a pre-defined curve in order to
yields a target BTP. Also in this case the manipulated
variable is the strand speed.
The new approach presented in the paper is based
on fuzzy rule-based expert systems and exploits the
charging gates as controlled variables. Two different
control strategies will be presented and discussed as
well as an innovative advisory system that supports
the plant operators in the control of the plant.
The paper is organized as follows. Section 2 de-
scribes the two control strategies while the advisory
system is presented in Section 3. Section 4 presents
the results of the on-the-plant tests and the Section 5
is devoted to the conclusion.
2 CONTROL STRATEGIES
Some mathematical models have been developed
in order to cope with the dynamic of the sinter-
ing process in an analytical way. A first attempt
has been made in (Young, 1977) while a differ-
ent perspective has been developed in (Augustin
et al., 1995) and (de Castro et al., 2012). A
different approach based on multiple-valued logic
is the core of the present paper and concepts of
fuzzy sets (Zadeh, 1965), fuzzy control (Lee, 1990)
(Pedrycz, 1989) (Passino and Yurkovich, 1998) and
expert systems (Jackson, 1998) (Durkin, 1998) are
used to develop the strategies and to build the advi-
sory system.
2.1 Overview of the Sintering Machine
The transversal direction of the strand can be divided
into four segments denoted by A, B, C and D. Each of
them covers the overall length of the machine and it
is about one meter wide, so that they cover the overall
Figure 1: Sketch of the macro-zones A,B and C of the
plant.
23 24 25 26 27 28
C
Figure 2: Sketch of the grid of thermocouples.
width of the strand. Regarding the longitudinal direc-
tion, three differentmacro-zonescan be pointed out as
depicted in Figure 1 and described in the following:
• charging zone (A) at the very beginning of the
strand;
• permeabilities zone (B) after the ignition hood at
the 3
rd
wind box;
• burn-through points zone (C ) at the end of the bed
covering a wide area of about 48 m
2
.
Within the macro-zone A the feed hopper, 6
charging gates and 6 infrared sensors can be found,
while the permeability sensors, which take 4 differ-
ent permeability measurements along the transversal
direction of the strand and that are indicated in the
following as K
A
, K
B
, K
C
, K
D
, are located within the
macro-zone B. Finally, in the last zone (C ) a regular
grid of thermocouples has been installed, such as de-
picted in Figure 2 that measures 24 temperature val-
ues: among them, the maximum one of each segment
is the associated BTP, thus finally there are 4 BTP val-
ues indicated as BTP
A
, BTP
B
, BTP
C
, BTP
D
.
From the point of view of the plant operational
practice, it would be advisable that the maximum
value of temperature is reached for all the segments
in correspondenceto approximatelythe same distance
from the strand end, as this implies that the sintering
process is quite homogeneous in all the portions of
the strand itself.
A preparatory statistical analysis conducted on
historical data coming from the plant has put
into evidence that the transversal alignment of
FuzzyControlofaSinteringPlant
69

BTP
A
, .. ., BTP
D
is related to a specific configuration
of K
A
, ..., K
D
. Thus, the idea behind the strategies is
to control the charging gates in order to obtain the
suitable permeability configuration in the macro-area
B.
Indeed, as the permeability configuration is sup-
posed to be symmetric, the difference between the
external permeabilities (K
A
, K
D
) and the internal ones
(K
B
, K
C
) can leads to crucial information about the
suitable configuration to be obtained.
Thus, in order to pursue such investigation, the
following 4 permeability ratios (K
r
) have been de-
fined:
(r
1
,r
2
,r
3
,r
4
)
T
=
K
A
K
D
,
K
B
K
C
,
K
A
K
B
,
K
D
K
C
T
. (1)
2.2 Description of the Strategies
Two control strategies have been designed, which
both aim at maximizing the increase of the average
permeability. The first strategy (‘a’) takes into ac-
count only this target; the second one (‘b’) takes also
into account the stress on the actuator and tries to min-
imize the movement of each gate, namely, if more
actions involving different gates are equally physi-
cally feasible, this latter strategy suggests the action
that produces the minimum displacement of the gates
from their current position.
Variables and symbols for both strategies are sum-
marized in Table 1 and a description of the first strat-
egy (‘a’) is the following:
1. Gates and Infrared Indices: the gate and the in-
frared values are normalized using its operative
limits (G
min
, G
max
, IR
min
, IR
max
);
2. Control Coefficients: four control coefficients
that express the contribution of each couple of
gates (i.e. 1,2 - 2,3 - 4,5 - 5,6) on each segment of
the bed are computed using the above indices;
3. Action Indices: four “action-indices” that con-
tain the information about the operations to per-
form on each couple of gates (e.g. a value less
than zero indicates that the gates of a couple need
to be closed) are computed and limited between
suitable thresholds (c
min
, c
max
);
4. Targets Computation: four different target per-
meability profiles, namely 4 different vectors of
4 entries each, are obtained using the permeabil-
ity ratios K
r
; the i-th element of the i-th vector is
obtained by imposing K
target
K
i
(i) = K
t
(i)while the
other elements are calculated using K
r
; the equa-
tions (2) show the computations for the first (i= 1)
profile:
K
target
K
1
(1)
def
= K
target
A
= K
t
(1) ≡ K
A
(2a)
K
target
K
1
(2)
def
= K
target
B
= K
target
A
/r
3
(2b)
K
target
K
1
(3)
def
= K
target
C
= K
target
B
/r
2
(2c)
K
target
K
1
(4)
def
= K
target
D
= K
target
A
/r
1
(2d)
where the relation (2a) concern the imposed ele-
ments (i = 1), while the formulas (2b)-(2d) con-
cern the computed elements of the profile;
5. Gaps Between Current and Target: for each
target profile the gaps between the current pro-
file and the target is evaluated, obtaining 4 dif-
ferent vectors of 4 entries each that are computed
according to the following equations, where i =
1,..., 4:
K
gaps
K
i
(1) = K
A
− K
target
K
i
(1) (3a)
K
gaps
K
i
(2) = K
B
− K
target
K
i
(2) (3b)
K
gaps
K
i
(3) = K
C
− K
target
K
i
(3) (3c)
K
gaps
K
i
(4) = K
D
− K
target
K
i
(4) (3d)
6. Control Amount for Each Couple of Gates: for
each vector of gaps the control amount values to
be applied on each couple of gates is calculated by
obtaining four vectors with four elements each;
7. Calculate the Feasibility: for each target profile
a feasibility coefficient is computed informing if
the related action on the couple of gates are phys-
ically feasible or not (e.g. it is required to close a
gate that it is already completely closed);
8. Calculate the Increase of the Average Perme-
ability: for each target profile the gains of the
average values are evaluated in order to use these
values as performance indicators; each of them is
related to a vector of control amount values so that
the better the control on the gates the higher will
be the index.
9. Select the Actions: among some target profile all
equally physically feasible, it is selected the one
which optimizes the performance indicator gain-
ing the four control amount values denoted by u
12
,
u
23
, u
45
and u
56
.
In Figure 3 the conceptual diagram of control strategy
‘a’ is reported.
The description of strategy ‘b’ is similar to the one
of the strategy ‘a’ where the point 8 is modified as
follows:
8. Calculate the Stress on the Actuator: for each
target profile, the stress produced on the actuator
is evaluated by summing the overall gaps of the
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
70
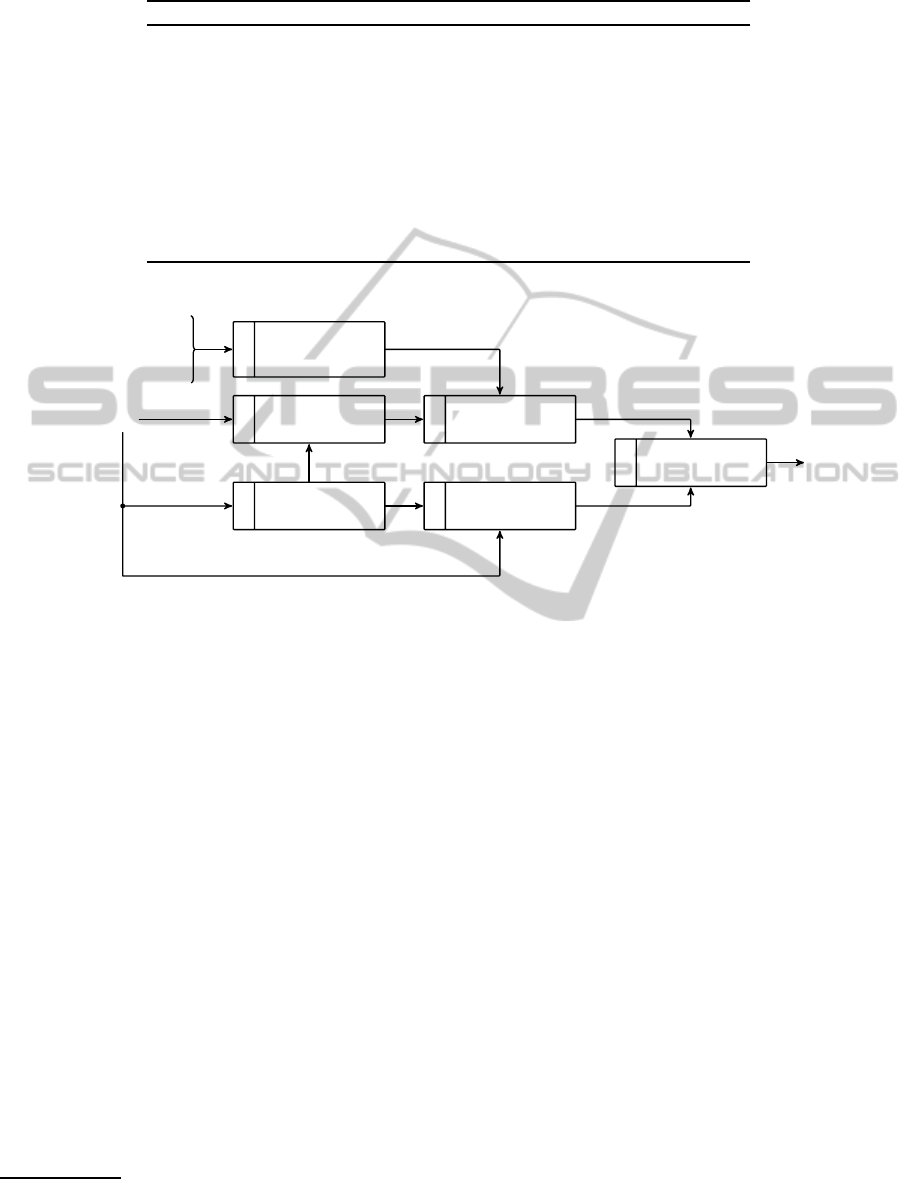
Table 1: Symbols used within the control strategies.
Symbol Meaning
†
G
t
Opening percentage of the gates
IR
t
Measure of the height of the sinter bed along the transversal direction
K
t
Permeability values i.e. K
t
=(K
1
, .. ., K
4
)
T
≡(K
A
, . .., K
D
)
T
K
r
Permeability ratios i.e. K
r
≡ (r
1
,r
2
,r
3
,r
4
)
T
K
target
K
i
Permeability values computed using K
r
by imposing
K
target
K
i
(i) = K
t
(i), i = 1,. .., 4
G
min
,G
max
Working range limits of the gates
IR
min
, IR
max
Minimum and maximum allowed height of the sinter bed
c
min
, c
max
Suitable thresholds
Y Selected control actions
†
where (·)
t
means that the values are taken at the current time instant i.e. they are on-line values.
G
t
, G
min
, G
max
IR
t
, IR
min
, IR
max
c
min
, c
max
1
2
3
calculate
indices
K
t
5
calculate
gaps
6
7
control and
feasibility
9
select
actions
u
12
u
23
u
45
u
56
4
calculate
target
⋆
8
calculate incr.
of av. perm.
⋆
Also use K
r
as input
Figure 3: Conceptual scheme of the first control strategy.
profile
1
in order to use these values (one for each
target profile) as performance indicators; each of
them is related to a vector of control amount val-
ues so that the better the control on the gates the
lower will be the index.
Thus, the conceptual diagram of the second con-
trol strategy is analogous to the one of the strategy ‘a’
except for the block number 8.
3 ADVISORY SYSTEM
The new value of the gates, required to reach the tar-
get permeability profile, can be computed through the
following relations:
G
new
(1) = G
t
(1) + 0.5u
12
, (4a)
G
new
(2) = G
t
(2) + 0.5u
12
+ 0.5u
23
, (4b)
G
new
(3) = G
t
(3) + 0.5u
23
, (4c)
G
new
(4) = G
t
(4) + 0.5u
45
, (4d)
G
new
(5) = G
t
(5) + 0.5u
45
+ 0.5u
56
, (4e)
G
new
(6) = G
t
(6) + 0.5u
56
(4f)
1
In fact, the gaps are related to the distance between the
current and the desired position of the gates.
where the coefficient of each term has been set heuris-
tically using the knowledge of the technicians’ exper-
tise.
Comparing the new values of the gates with the
current values, the advisory system is able to provide
information about the actions to be performed on all
of the charging gates. The actions are also related
to a rank number in order to inform about the most
promising of them.
The advisory system is an expert system (ES)
founded on multiple-valued logic with a rule base that
reproduce the knowledge of the plant operators. Thus
the system belongs to the larger family of the Fuzzy
Rule-Based Expert Systems (FRBES) (Geyer-Schulz,
1995).
The system is designed using the zero-order Tak-
agi-Sugeno-Kang (TSK) model (Takagi and Sugeno,
1985) where the j-th fuzzy rule (R
j
) of the form “IF
hpremisei THEN hconclusioni” is given by:
R
j
: IF (x is A
i
) AND/OR (y is B
i
) THEN z
j
= c
j
(5)
where x and y are the inputs, A
i
and B
i
are fuzzy sets
and c
j
is a crisp adjustable parameter.
The system evaluates each rule (implication) col-
lecting together the results (aggregation) in order to
FuzzyControlofaSinteringPlant
71

Table 3: Characteristic parameters µ and σ of the linguistic terms.
FIS
1,3,4,6
FIS
2,5
DG DGN DG DGSx DGDx
NEG −1,0.34 −1,0.34 −1,0.34 −1, 0.34 −1,0.34
NUL 0,0.1 0,0.1 0,0.16 0,0.14 0,0.13
POS 1,0.34 1,0.34 1,0.34 1,0.34 1,0.34
Table 4: Rules for the FIS
1,3,4,6
.
DGN is NEG DGN is POS DGN is NUL
DG is NEG −1 0 −1
DG is POS 0 1 1
DG is NUL 0 0 0
produce a unique output fuzzy set. The crisp value
extracted from this fuzzy set (defuzzification) repre-
sents the output of the entire inference process.
The aggregation and the defuzzification tasks can
be merged in a unique operation in the TSK model as
follows:
z =
N
∑
j=1
w
j
c
j
N
∑
j=1
w
j
, with w
j
= F(µ
i
,ν
i
) (6)
where N is the number of rules, w
j
is the firing
strength of the j-th rule (i.e. the “degree of truth” of
the hpremisei), F is the method that implements the
AND operator (F is a t-norm) or the OR operator (F
is a t-conorm), µ
i
is the membership degree of x to A
i
and ν
i
is the membership degree of y to B
i
.
The system is composed of 6 specialized fuzzy
inference systems (FISs), one for each gate (FIS
i
,
i = 1,. .. ,6), whose inputs are the differences ∆G
i
=
G
new
(i) − G
t
(i) (after a proper normalization stage
forcing any crisp input to lie in the range [−1,1]).
Moreover, ∆G
2
is in input to both the FIS
1
and the
FIS
3
as additional input as well as ∆G
5
is in input to
both the FIS
4
and the FIS
6
. These additional gaps will
be denoted by the DGN term within the rules.
The FIS
2
has ∆G
1
and ∆G
3
as additional inputs
as well as the FIS
5
receives ∆G
4
and ∆G
6
. These
additional gaps will be denoted, respectively, by the
DGDx and DGSx terms within the rules. Table 2 sum-
marizes the inputs of each FIS.
Table 2: Inputs of each fuzzy inference system.
∆G
1
∆G
2
∆G
3
∆G
4
∆G
5
∆G
6
FIS
1
• •
FIS
2
• • •
FIS
3
• •
FIS
4
• •
FIS
5
• • •
FIS
6
• •
The inputs of the FIS
1,3,4,6
are 2 linguistic vari-
ables, while the inputs of the FIS
2,5
are 3 linguistic
variables. For each input variable, 3 linguistic terms
(i.e. fuzzy sets) are defined: ‘Negative’(NEG), ‘Null’
(NUL) and ‘Positive’ (POS). The membership func-
tions of all the fuzzy sets are bell-shaped functions
whose parameters (µ,σ) have been heuristically set as
described in Table 3.
The rule bases for the systems have been obtained
after fruitful discussions with the plant operators and
considering also the operative practices of the opera-
tors too.
All the rules for the FIS
1,3,4,6
are shown in Table 4
while in Table 5 to 7 are shownthe rules for the FIS
2,5
.
In all the rule bases the numerical value of the out-
put means that the gate must be closed (− 1) or opened
(1) or, finally, that no operation must be performed on
the gate (0). The
∏
(x,y) = x∗ y operator is the t-norm
that implements the AND connection of each rule and
the relation (6) is used to defuzzify the inferred output
fuzzy set.
4 EXPERIMENTAL RESULTS
Two different scenarios have been considered for the
plant tests. The first one (“short period scenario”)
takes into account a period of 4 hours using the strat-
egy ‘a’ for the first 2 hours and the strategy ‘b’ during
the last 2 hours.
Some characteristic conditions can be highlighted
during the tests within this scenario: (a) no stoppage
of the strand occurred; (b) the percentages of lime and
limestone within the mix were fixed; (c) the ratio be-
tween the speed of the drum feeder and the speed of
the strand was constant; (d) the moisture of the mix
was kept as constant as possible.
The qualitative results of the first session showed
that the strategy ‘a’ leads to an actual increment of
the average permeability and thus to a better yield of
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
72

Table 8: Time intervals of the long period tests.
Test number Duration (h) Time interval Control Strategy
1 12 Day 1 (from 00:00 to 12:00) Technicians Expertise
2 12 Day 1 (from 12:00 to 00:00) ‘a’
3 12 Day 2 (from 00:00 to 12:00) Technicians Expertise
4 12 Day 2 (from 12:00 to 00:00) ‘b’
5 12 Day 3 (from 00:00 to 12:00) Technicians Expertise
6 12 Day 3 (from 12:00 to 00:00) ‘a’
7 12 Day 4 (from 00:00 to 12:00) ‘b’
Table 5: Rules for the FIS
2,5
when DGSx is POS.
DGSx is POS
DGDx is DGDx is DGDx is
NEG POS NUL
DG is NEG 0 0 −1
DG is POS 0 1 0
DG is NUL 0 0 0
Table 6: Rules for the FIS
2,5
when DGSx is NUL.
DGSx is NUL
DGDx is DGDx is DGDx is
NEG POS NUL
DG is NEG 0 −1 −1
DG is POS 1 0 1
DG is NUL 0 0 0
Table 7: Rules for the FIS
2,5
when DGSx is NEG.
DGSx is NEG
DGDx is DGDx is DGDx is
NEG POS NUL
DG is NEG −1 0 0
DG is POS 0 0 1
DG is NUL 0 0 0
the plant: this can be assessed considering the lower
Internal Return Fines (IRFs) consumption and thus a
lower wet coke consumption.
During the tests, the plant operators confirmed
that: (i) the actions proposed by the system have been
always fully safe despite the change of the operational
conditions in which each decision has been taken;
(ii) the operations have been always coherent with the
personnel’sexpertise. Thus, in the short period the ad-
visory system proved to behave according to the best
practice of the operators. Therefore, it is expected
that, in the long period, the automatic implementation
of such system will lead to improvement of the pro-
cess performances with a reduction of the operators’
effort.
The second scenario (“long period scenario”) con-
siders a period of 84 hours and compares the sys-
tem behavior during intervals when one of the devel-
oped control strategies was applied to intervals when
none of them was used and the plant was controlled
by exploiting only the expertise of the plant techni-
cians. The detailed description of each period of time
is summarized in Table 8.
The long period of eighty-four hours is the best
one that can be obtained minimizing the external in-
fluences such as, for example, a different chemical
composition in the mix caused by a different Blend
Iron Ore (BIO) in the mix. In Taranto, in fact, the typ-
ical amount of BIO is of 160000-180000 tonnes and
they are used within the mix during a typical period
of five days. Thus, the tests have been performed after
a suitable stabilization period after the change of the
BIO. Moreover, during the first day of the long period
test a significant stoppage of the strand occurred. In
order to take this fact into account, the results have
been computed by using only the data deriving from
a stable condition of the process (i.e. about 90 min.
after the restart).
Let ∆S be the amount of the produced sinter (in
tonnes), σ
C
the specific coke consumption (i.e. the
amount of the coke consumption - measured in Kg
- per tonne of produced sinter) and σ
IRF
the spe-
cific IRF production (i.e. the amount of produced
IRFs production - measured in Kg - per tonne of pro-
duced sinter); 3 significant Key Performance Indica-
tors (KPIs) can be defined as follows (where (·)/h
means “per hour”):
KPI
1
i.e. Sinter Production =
∆S
h
, (7a)
KPI
2
i.e. Wet Coke Consumption =
σ
C
h
, (7b)
KPI
3
i.e. IRF Production =
σ
IRF
h
. (7c)
In order to evaluate the goodness of the results the
trends of the KPIs have been evaluated. In particular,
the IRFs production that can be related directly to the
yield of the plant through the following equation:
Yield(%) = 100− 0.1σ
IRF
. (8)
The results of the long period tests are numerically
described in Table 9: using the strategy ‘a’ an aver-
age increment of the produced sinter and an average
FuzzyControlofaSinteringPlant
73

Table 9: Experimental results.
Control Strategy KPI
1
KPI
2
KPI
3
Expertise 4.25 -0.019 6.60
Strategy ‘a’ 2.38 -0.236 -6.75
Expertise -6.25 0.208 4.66
Strategy ‘b’ 1.45 -0.062 -2.50
Expertise -1.18 0.048 2.17
Strategy ‘a’ 3.92 -0.015 -0.43
Strategy ‘b’ -5.76 -0.231 -0.93
Expertise (mean) -1.06 0.08 4.48
Strategy ‘a’ (mean) 3.15 -0.13 -3.59
Strategy ‘b’ (mean) -2.16 -0.15 -1.72
reduction of the coke consumption as well as of the
IRFs production have been gained. The strategy ‘b’,
on the other hand, led to comparable results regarding
the coke consumption and the IRFs production, but
caused an average decrement of the productivity.
During both the short and the long period tests the
opinions of the technicians have been taken into ac-
count in order to evaluate the practical goodness of
the strategies as well as the KPI’s variations.
The behaviour most frequently used by the plant
experts was very similar to that of the strategy ‘b’ and
in contrast with the strategy ‘a’. Indeed, the strat-
egy ‘a’ takes into account only the average perme-
ability and whenever a variation of the gates posi-
tion is required in order to improve the permeabil-
ity, the variation is reported to the gates. This leads
to frequent variation in the gates positions and some-
times in abrupt changes. The technicians, on the other
hand, use a more conservative approach that tends to
perform slight modification in the gates position and
rarely abrupt changes.
Summing up the results of the tests of the two
control strategies: strategy ‘a’ gives better automatic
results, but it is less coherent to the technicians’
standard operating practice, thus they can experience
higher efforts in order to follow the plant behavior
when this control strategy is applied. Strategy ‘b’
leads to fairly good results, but it is more coherent
to the standard operating practice.
Finally, it can be noticeable that the advisory sys-
tem has been designed to be improved through its use,
as the overall software system supports data collec-
tion and analysis. After a longer period of use it will
be possible to refine the performances of the proposed
system using the same statistical parameters that sup-
plied the system.
5 CONCLUSION
A new approach based on fuzzy rule-based expertsys-
tems and a new advisory system to control the charg-
ing gates of a sinter plant is presented. Two new con-
trol strategies have been developed and tested on the
field.
Strategy ‘a’ is more invasive within the process
operational conditions, as it aims at maximizing the
productivity without any kind of trade-off. It can be
used when the plant is characterized by lower produc-
tivity (e.g. the plant is restarted after a stoppage): in
these cases the greater the control amount, the shorter
the time elapsed before reaching fair operating condi-
tions.
On the other hand, strategy ‘b’ is more conser-
vative, as it aims at maximizing the productivity but
considers also the stress on the gates’ actuators and
produces less perturbation in the operating conditions
with respect to the other strategy. It can be used when
the plant is characterized by higher productivity and
the machine shows a higher sensitivity to the changes
on the gates.
Real-time tests are still ongoing at the sintering
plant of ILVA S.p.A. (Taranto Works, Italy) and satis-
factory results confirm the goodness of the automatic
control system.
Future work will deal with the development of a
new strategy combining the strong points of the two
developed ones. In detail, this strategy can select au-
tomatically the use of the strategy ‘a’ during the lower
productivity phase of the plant switching on the other
strategy (‘b’) during the phase with high productiv-
ity and vice-versa. In this way a single strategy can
take the best advantages from the two developed ones
achieving good results during all the production phase
of the plant.
ACKNOWLEDGEMENTS
The work described in the present paper was devel-
oped within the project entitled ”New measurement
and control techniques for total control in iron ore
sinter plants” ToSiCo (Contract No. RFSR-CT-2009-
00001) that has received funding from the Research
Fund for Coal and Steel of the European Union. The
sole responsibility of the issues treated in the present
paper lies with the authors; the Commission is not re-
sponsible for any use that may be made of the infor-
mation contained therein.
REFERENCES
Arbeithuber, C., J¨orgl, H. P., and Raml, H. (1995). Fuzzy
control of an iron ore sintering plant. Control Engi-
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
74

neering Practice, 3(2):1669–1674.
Augustin, M., Arbeithuber, C., and J¨orgl, H. P. (1995).
Modeling and simulation of an iron ore sinterstrand.
In EUROSIM, pages 873–878.
de Castro, J. A., Sazaki, Y., and Yagi, J. (2012). Three
dimensional mathematical model of the iron ore sin-
tering process based on multiphase theory. Materials
Research, 15(6):848–858.
Durkin, J. (1998). Expert Systems: Design and Develop-
ment. Macmillan Publishing Company.
Geyer-Schulz, A. (1995). Fuzzy Rule-Based Expert Systems
and Genetic Machine Learning. Physica-Verlag.
Hu, J. Q. and Rose, E. (1997). Predictive fuzzy control ap-
plied to the sinter strand process. Control Engineering
Practice, 5(2):247–252.
Jackson, P. (1998). Introduction to Expert Systems. Addison
Wesley, 3rd edition.
Kanjilal, P. P. and Rose, E. (1986). Application of adaptive
prediction and control method for improved operation
of the sintering process. Ironmaking and Steelmaking,
13(6):289–293.
Lee, C. C. (1990). Fuzzy logic in control systems: Fuzzy
logic controller - parts 1 and 2. IEEE Transactions on
Systems, Man and Cybernetics, 20(2):404–435.
Passino, K. M. and Yurkovich, S. (1998). Fuzzy Control.
Addison Wesley.
Pedrycz, W. (1989). Fuzzy Control and Fuzzy Systems. Re-
search Studies Press Ltd.
Takagi, T. and Sugeno, M. (1985). Fuzzy identification of
systems and its applications to modelling and control.
IEEE Transactions on Systems, Man and Cybernetics,
15(1):116–132.
Young, R. W. (1977). Dynamic mathematical model of
a sintering process. Ironmaking and Steelmaking,
4(6):321–328.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8:338–353.
FuzzyControlofaSinteringPlant
75
