A Fusion Approach to Computing Distance for Heterogeneous Data

Aalaa Mojahed

1,2

and Beatriz de la Iglesia

Norwich Research Park, University of East Anglia, Norwich, Norfolk, U.K.

King Abdulaziz University, Faculty of Computing and Information Technology, Jeddah, Saudi Arabia

Keywords:

Heterogeneous Data, Distance Measure, Fusion, Clustering, Uncertainty.

Abstract:

In this paper, we introduce heterogeneous data as data about objects that are described by different data types,

for example, structured data, text, time series, images etc. We provide an initial deﬁnition of a heterogeneous

object using some basic data types, namely structured and time series data, and make the deﬁnition extensible

to allow for the introduction of further data types and complexity in our objects. There is currently a lack of

methods to analyse and, in particular, to cluster such data.

We then propose an intermediate fusion approach to calculate distance between objects in such datasets. Our

approach deals with uncertainty in the distance calculation and provides a representation of it that can later

be used to ﬁne tune clustering algorithms. We provide some initial examples of our approach using a real

dataset of prostate cancer patients including visualisation of both distances and uncertainty. Our approach is a

preliminary step in the clustering of such heterogeneous objects as the distance between objects produced by

the fusion approach can be fed to any standard clustering algorithm. Although further experimental evaluation

will be required to fully validate the Fused Distance Matrix approach, this paper presents the concept through

an example and shows its feasibility. The approach is extensible to other problems with objects represented

by different data types, e.g. text or images.

1 INTRODUCTION

Big data produced daily by digital technology is not

only huge in volume but also has the properties of ve-

locity and variety (Laney, 2001). Variety refers to the

presence of heterogeneous data types such as text, im-

ages, audio, structured data, time series etc. In this

research, we set out to deal explicitly with variety in

the data. In particular, we address the complexity that

occurs when objects to be analysed are described by

multiple data types. This is motivated by our need to

cluster complex patient data relating to prostate can-

cer. In our dataset, a patient may be characterised

by structured data from the administrative systems,

images from radiology, text reports that accompany

images, others text reports containing, for example,

discharge information, results of blood tests which

may be interpreted as time series, etc. The analysis

of such complex objects may sometimes be beneﬁ-

cial, yet currently it is under-addressed in data min-

ing research. Mining such data collections may reveal

interesting associations that would remain concealed

if researchers investigate only one type of data. For

example, clustering may reveal associations between

values of PSA over time (a test relevant in the con-

text of prostate cancer) and values of other blood test

result and other patient characteristics (e.g. Gleason

score, tumor staging at diagnosis, treatment type or

outcome).

Clustering (Jain et al., 1999) is an unsupervised

learning technique where patterns or objects are clus-

tered into related groups based on some measures of

(dis)similarity, which play a critical role. Different

data types rely on different (dis)similarity measures.

Most of the available, reliable and widely used mea-

sures can only be applied to one type of data.

In this context, it is essential to construct an ap-

propriate measure for comparing complex objects that

are described by components from diverse data types.

Once a measure of distance is deﬁned, and a Dis-

tance Matrix (DM) representing the distance between

the objects can be obtained, complex objects can be

manipulated by means of any of the popular cluster-

ing algorithms. The aim of this paper is therefore to

propose a distance measure for complex objects de-

scribed by heterogeneous data. We review current re-

search in this area and propose a new intermediate fu-

sion approach that calculates distances between com-

plex objects. We use our medical example to compute

and visualise DMs according to the fusion approach.

269

Mojahed A. and de la Iglesia B..

A Fusion Approach to Computing Distance for Heterogeneous Data.

DOI: 10.5220/0005083702690276

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2014), pages 269-276

ISBN: 978-989-758-048-2

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

The rest of this paper is organized as follows. Sec-

tion 2 provides an overview and a discussion of re-

lated research. In Section 3, a precise deﬁnition of

heterogeneous data in our context is given. The pro-

posed approach for computing DMs is presented in

Section 4. An example of our method being applied

to a real dataset is presented in Section 5. This is fol-

lowed by our conclusions and suggestions for further

research.

2 RELATED WORK

Data heterogeneity has different meanings in different

environments and is generally associated with some

form of complexity. For example and not as a limi-

tation, it may describe Web data (Zeng et al., 2002)

which refers to the diversity of information associ-

ated with webpages. Another example, datasets col-

lected in scientiﬁc, engineering, medical or social ap-

plications (Skillicorn, 2007) which refers to data gen-

erated from multiple processes. Also, in the con-

text of multidatabase systems heterogeneity may re-

fer to structural and representational discrepancies

(Kim and Seo, 1991) or semantic discrepancies (Goh,

1996). However, it is clear that complexity is inherent

in any type of heterogeneous data.

We deﬁne heterogeneity in a narrow sense as re-

lating to real world complex objects that are described

by different elements where each element may be of

a different data type. Returning to our previous ex-

ample, a ’patient’ may be described by elements con-

taining: structured data (e.g. a set of values for demo-

graphic attributes); semi-structure data ( e.g. a diag-

nostic text report); time series data (e.g. a set of blood

test results over a period of time); and some image

data (e.g. an x-ray image). Note that an object may

have entire elements missing (e.g. a complete set of

values for a particular blood test that the patient did

not take) or values within the element missing (e.g.

some demographic values are not recorded). This

type of heterogeneity makes no assumptions about the

source of the data. It could be an individual homo-

geneous database system or multiple heterogeneous

datasets. However, all available data represents a dif-

ferent description, an element, of the same object. We

are not referring to relationships between classes of

entities or objects but to relationships between objects

of the same class. Each element could be generated

from a different process but the elements are under-

stood as being complementary to one another and de-

scribing the object in full. Thus they all are charac-

terised by sharing the same Object Identiﬁer (O.ID).

Much of the work in this area relates to the cluster-

ing of multi-class interrelated objects, that is, objects

deﬁned by multiple data types and belonging to dif-

ferent classes that are connected to one another. Fu-

sion approaches (Bostr

om et al., 2007) are often used

to deal with this type of data as they can combine di-

verse data sources even when they differ in terms of

representation. Early fusion approaches focused on

the analysis of multiple matrices and formulated data

fusion as a collective factorisation of matrices. For ex-

ample, Long et al. (2006) proposed a spectral cluster-

ing algorithm that uses the collective factorisation of

related matrices to cluster multi-type interrelated ob-

jects. The algorithm discovers the hidden structures

of multi-class/multi-type objects based on both fea-

ture information and relation information. Ma et al.

(2008) also used fusion in the context of a collabo-

rative ﬁltering problem. They propose a new algo-

rithm that fuses a user’s social network graph with a

user-item rating matrix using factor analysis based on

probabilistic matrix factorisation. Some recent work

on data fusion (Evrim et al., 2013) has sought to un-

derstand when data fusion is useful and when the

analysis of individual data sources may be more ad-

vantageous.

According to the stage at which the fusion proce-

dure takes place, data fusion approaches are classi-

ﬁed into three categories (Maragos et al., 2008): early

integration, late integration and intermediate integra-

tion. In early integration, data from different modali-

ties are concatenated to form a single dataset. Accord-

ing to

Zitnik and Zupan (2014), this fusion method

is theoretically the most powerful approach but it ne-

glects the modular structure of the data and relies on

procedures for feature construction. Intermediate in-

tegration is the newest method. It retains the structure

of the data and concatenates different modalities at

the level of a predictive model. In other words, it ad-

dresses multiplicity and merges the data through the

inference of a joint model. The negative aspect of in-

termediate integration is the requirement to develop a

new inference algorithm for every given model type.

However, according to some researchers (

Zitnik and

Zupan, 2014; van Vliet et al., 2012; Pavlidis et al.,

2002) the intermediate data fusion approach is very

accurate for prediction problems and may be very

promising for clustering. In late integration, each data

modality gives rise to a distinct model and models are

fused using different weightings. Greene and Cun-

ningham (2009), for example, present an approach for

clustering with late integration using matrix factorisa-

tion. Others have derived clustering using various en-

semble methods (Dimitriadou et al., 2002; Strehl and

Ghosh, 2003) to arrive at a consensus clustering.

In our research, we explore intermediate integra-

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

270

tion by merging DMs prior to the application of clus-

tering algorithms. A number of DMs are produced to

assess (dis)similarity between heterogeneous objects;

each matrix represents distance with regards to a sin-

gle element. We then fuse the DMs for the different

elements together to generate a single fused DM for

all objects. We merge the DMs using a weighted lin-

ear scheme to allow different elements to contribute to

the clustering according to their importance. Previous

research (Evrim et al., 2013; Pavlidis et al., 2002) has

found that combining data types is not always useful

to knowledge extraction because some data types may

introduce noise into the model. Accordingly, in our

future research we will need to measure how useful

each element is to our clustering results. We expect

that further work will also concentrate on compar-

ing our approach with other intermediate fusion algo-

rithms (e.g., multiple kernel learning (Yu et al., 2010)

and matrix factorization (

Zitnik and Zupan, 2014)) as

well as early and late fusion methods. The advantage

of our approach over other intermediary fushion ap-

proaches is that the fused distance matrix can be used

by well established clustering algorithms with little

modiﬁcation. The only modiﬁcation required may be

to take advantage of the additional information on un-

certainty provided by the companion matrices in the

clustering algorithm.

3 PROBLEM DEFINITION

In this research, we deﬁne a heterogeneous dataset, H,

as a set of objects such that H = {O

, O

, ..., O

, ...,

}, where N is the total number of objects in H and

is the i

object in H. Each object, O

, is deﬁned

by a unique Object Identiﬁer, O

.ID. We use the dot

notation to access the identiﬁer and other component

parts of an object. In our heterogeneous dataset ob-

jects are also deﬁned by a number of components or

elements O

= {E

,...,E

}, where M rep-

resents the total number of elements and E

repre-

sents the data relating to E

for O

. Each full element,

, for 1 ≤ j ≤ M, may be considered as represent-

ing and storing a different data type. Hence, we can

view H from two different perspectives: as a set of

objects containing data for each element or as a set

of elements containing data for each object. Either

representation will allow us to extract the required in-

formation. For example, O

would refer to all the el-

ements available for object 3 (e.g a speciﬁc patient

with a given ID); O

would refer to the second el-

ement for object three (e.g. a set of hemoglobin blood

test results for a speciﬁc patient); E

would refer to

all of the objects’ values for element 2 (e.g. all of the

hemoglobin blood results for all patients) .

We begin by considering a number of data types,

including Structured Data (SD) and Time Series data

(TS):

SD A heterogeneous dataset may contain a (generally

only one) SD element, E

. In this case, there is

a set of attributes E

= {A

,...,A

} deﬁned

over p domains with the expectation that every ob-

ject, O

, contains a set of values for some or all of

the attributes in E

. Hence, E

is a N × p ma-

trix in which the columns represent the different

attributes in E

and the rows represent the values

of each object, O

, for the set of attributes in E

For example, O

refers to the value of A

for O

in the SD element. The domain for SD is

that considered in relational databases, e.g.: prim-

itive domains such as boolean, numeric or char;

strings domains such as char(n) or varchar(n); and

date and time domains.

TS The heterogeneous dataset may also con-

tain one or more time-series elements:

TS1

,...,E

TSg

,...,E

TSq

. A TS is a tempo-

rally ordered set of r values which are typically

collected in successive (possibly ﬁxed) intervals

of time: E

TSg

= {(t

),...,(t

)}

such that v

is the ﬁrst recorded value at time

, v

is the l

recorded value at time t

, etc.,

∀l,v

∈ ℜ. Any TS element, E

TSg

, can be rep-

resented as a vector of r time/value pairs. Note,

however, that r is not ﬁxed, and thus the length

of the same time-series element can vary among

different objects.

This deﬁnition of an object is extensible and al-

lows for the introduction of further data types such

as images, video, sounds, etc. Moreover, it can

be concluded from the above deﬁnition that any ob-

ject O

∈ H might contain more than one element

drawn from the same data category. In other words,

a particular object O

may be composed of a num-

ber of SDs and/or TSs. Incomplete objects are per-

mitted, where one or more of their elements are ab-

sent. Figure 1 demonstrates two different views of

our heterogeneous dataset: an elements’ view and

an objects’ view. In addition, it shows our interme-

diary fusion model for assessing the (dis)similarity

between heterogeneous objects. The data can be

stored in a way that allows easily to alternate be-

tween these two views, i.e. the data of a particu-

lar element, say E

, can be accessed as well as the

data for a particular object, say O

. It may be pos-

sible, for example to store the data as sets of tu-

ples < O.ID,E .ID,Data Type, f ield,value > where

for a SD element the ﬁeld contains the name of the

AFusionApproachtoComputingDistanceforHeterogeneousData

271

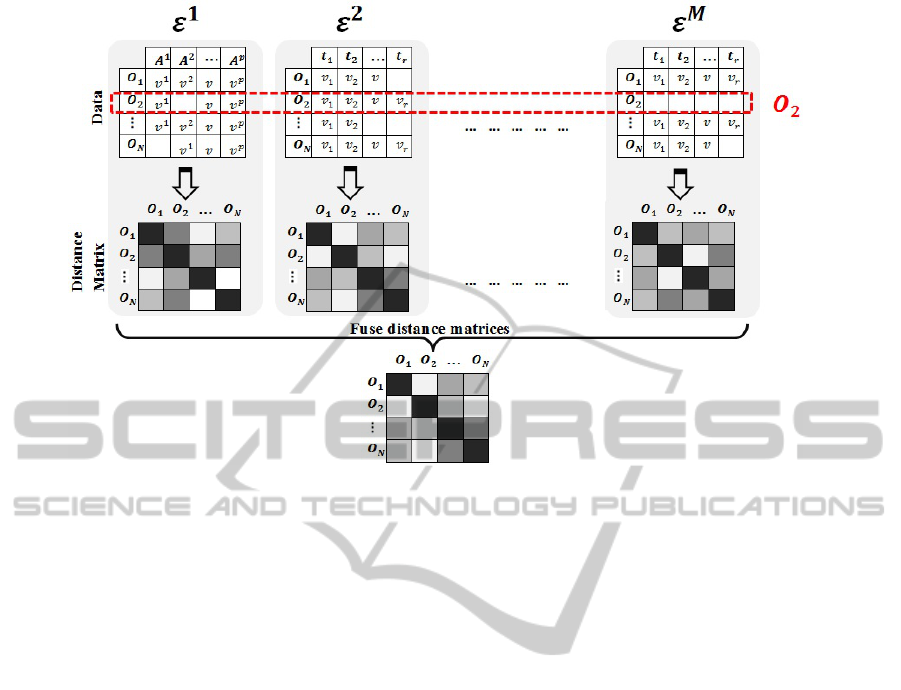
Figure 1: Heterogeneous data representation: The red dashed rectangle shows the data relating to a particular object,O

whereas the matrices show various elements including a SD element,E

, and two TS elements,E

and E

. The lower part of

the diagram shows the fusion strategy that results from producing a distance matrix for each element and fusing them together

to create a unique distance matrix for all objects.

Attribute to be stored with its corresponding value,

whereas for a TS element the ﬁeld corresponds to

the time with its corresponding value. An exam-

ple of a patient data recorded in this way may be:

< Pat123,HISData,age,57 >,

< Pat123,HISData,weight,66 >,

< Pat123,HISData,tumourStage,3 >

< Pat123,BloodVitaminD,0,13.2 >

< Pat123,BloodVitaminD,30,13.6 >

< Pat123,BloodVitaminD,65,13.8 >

< Pat123,BloodCalcium,0,39 >

< Pat123,BloodCalcium,30,42 >

< Pat123,BloodCalcium,65,40 >

In this scenario, it is possible to distribute the data us-

ing a distributed ﬁle system and it is also possible to

then retrieve the whole dataset for an object or for an

element as required by an algorithm.

4 SIMILARITY MEASURES FOR

HETEROGENEOUS DATA

USING A FUSION APPROACH

Distance measures reﬂect the degree of (dis)similarity

between objects. From now on we refer to similar-

ity although similarity/dissimilarity are interchange-

able concepts. A variety of measures have been de-

veloped to deal with different data types. Heteroge-

neous data consisting of objects described by differ-

ent data types may require a new way of measuring

distance between objects. In this paper, we are re-

stricting ourselves to two data types: SD and TS data,

however, the approach may be extensible to further

data types. We propose to use a Similarity Matrix Fu-

sion (SMF) approach, as follows: 1. Deﬁne a suit-

able data representation to both describe the dataset

and apply suitable distance measures; 2. Calculate

the DMs for each element independently; 3. Consider

how to address data uncertainty; and 4. Fuse the DMs

efﬁciently into one Fusion Matrix (FM), taking ac-

count of uncertainty.

The main idea of SMF is to create a compre-

hensive view of distances for heterogeneous objects.

SMF computes and fuses DMs obtained from each of

the elements separately, taking advantage of the com-

plementarity in the data. Hence for every pair of ob-

jects, O

and O

, we begin by calculating entries for

each individual DM corresponding to one of the ele-

ments in the heterogeneous database, E

, as follows:

= dist(O

where in each case dist represents an appropriate dis-

tance measure for the given data type. When E

missing in O

or O

or both the value of DM

be-

comes null.

Appropriate distance measures are explored in

Section 4.1. The M DMs are later fused into one ma-

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

272

trix, FM, which expresses the distances between het-

erogeneous objects. Along with the process of fusing

DMs, data uncertainty needs to be addressed. Sec-

tion 4.3 describes our suggested solutions. Once we

have a FM representing distances between complex

objects, we can proceed to cluster heterogeneous ob-

jects using standard algorithms. This will be tackled

in further research.

4.1 Construction of DMs for Each

Element

The Standardized Euclidean distance (SEuclidean)

can be employed to measure the similarity for the SD

element because it works efﬁciently and is well estab-

lished, although other modalities could be explored as

necessary. The SEuclidean distance between SD ele-

ments requires computing the standard deviation vec-

tor S = {s

,...,s

}, where s

is the standard

deviation calculated over the z

attribute, A

, of the

SD element. SEuclidean between two objects, O

and

, is:

SEuclidean

∑

z=1

− O

)

To measure distance between TSs, we can use a

Dynamic Time Warping (DTW) approach that was

ﬁrst introduced into the data mining community in

1996 (Berndt and Clifford, 1996). DTW is a non-

linear (elastic) technique that allows similar shapes

to match even if they are out of phase in the time

axis. Ratanamahatana and Keogh (2005) investigated

the ability of DTW to handle sequences of variable

lengths and concluded that reinterpolating sequences

into equal lengths does not produce a statistically sig-

niﬁcant difference to comparing them directly using

DTW. Others (Henniger and Muller, 2007) have ar-

gued that interpolating sequences into equal lengths

is detrimental. We use DTW to assess the TS us-

ing their original lengths. The calculated distances

are normalized and this is achieved by normalizing

through the sum of both series’ lengths. To ex-

plain how to align two TSs using DTW, suppose the

lengths of E

T S

for O

and O

are r1 and r2 respec-

tively. First, we need to construct an r1 × r2 piece-

wise squared distance matrix. The k

element of this

matrix, W

, coresponds to the squared distance be-

tween the k

pair of values , v

and v

of TS ele-

ments of O

and O

respectively which is calculated

as (O

T S

− O

T S

)

. Then the DTW dis-

tance for E

T S

of O

and O

is deﬁned by the short-

est path through this matrix. The optimal path can be

found using dynamic programming (Ratanamahatana

and Keogh, 2005) that minimises the warping cost:

DTW

T S

= min

(

∑

k=1

All the computed distances in the M DMs need

to be normalized to lie in the range [0 − 1] since this

is essential in handling data uncertainty which is dis-

cussed in Section 4.3. Principally, our method is gen-

eral and can be extended to other data types by using

relevant distance measure, e.g. cosine similarity for

text elements or Earth Mover’s Distance for image el-

ements.

4.2 Computing the Fusion Matrix

Fusion of the M DMs for each element can be

achieved using a weighted average approach. Weights

are used to allow emphasis on those elements that

may have more inﬂuence on discriminating the ob-

jects. When all elements are to contribute equally to

the calculations, all weights can be set to 1. The fused

matrix representing the distance between two objects,

, can be deﬁned as:

∑

z=1

× DM

∑

z=1

∀i, j ∈ {1,2...N}. w

is the weight given to the z

el-

ement.

4.3 How to Handle Uncertainty

Uncertainty is inseparably associated with learning

from data. Cormode and McGregor (2008) reported

that combining data values, can be considered as a

source of uncertainty. Thus in our research the pro-

cess of measuring similarity can be affected by un-

certainty in a number of ways. First, we may be

comparing incomplete objects. Assessing similar-

ity for incomplete objects produces a null value in

when either O

and/or O

are missing for the

element. Secondly, a lack of coincidence (or dis-

cordance) in assessing the distance between objects

when using different elements may also introduce un-

certainty in the FM. For instance, O

and O

may

be considered as similar objects in some of the pre-

computed DMs but not in others, making the overall

similarity of the objects uncertain.

We propose a description for both types of uncer-

tainty as follows. For each pair of objects,O

and O

AFusionApproachtoComputingDistanceforHeterogeneousData

273

we compute the uncertainty associated with the FM

arising from missing information, UFM, as follows:

UFM

∑

z=1

(

1, DM

6= null

0, otherwise

With regards to the disagreement between DMs judg-

ments, we compute the uncertainty associated with

the FM, DFM, for each pair of objects,O

and O

, as

follows:

DFM

∑

z=1

(DM

− DM

)

where,

∑

z=1

In other words, UFM, calculates the proportion of

missing distance values in the DMs associated with

all elements for objects O

and O

, while DFM, cal-

culates the standard deviation of distance values in

the DMs associated with all elements for objects O

and O

. We now have two expressions of uncertainty,

UFM and DFM, associated with each value of the fu-

sion matrix, FM. Those values may be used separately

to ﬁlter data or combined together. We may wish to

use UFM and DFM individually to ﬁlter out uncer-

tain values according to different criteria, or we may

wish to report both values together, for example by

calculating the average of both measures as the uncer-

tainty associated with a given value of FM. To ﬁlter

out values we can set thresholds for each calculation

individually, i.e., ignoring cases where UFM ≥ φ

DFM ≥ φ

5 THE EXPERIMENTAL WORK

5.1 Dataset Used

A real dataset was used for the experiments. It ini-

tially included descriptions of a total of 1,904 patients

diagnosed with prostate cancer at the Norwich and

Norfolk University Hospital (NNUH), UK. It was cre-

ated by Bettencourt-Silva et al. (2011) by integrating

data from nine different hospital information systems.

Each patient’s data is represented by 26 attributes that

form the SD part of the data. They describe demo-

graphics (e.g. age, death indicator) and other disease

states (e.g. Gleason score, tumor staging). In addi-

tion, 23 different blood test results are recorded as TS

(e.g. Vitamin D, MCV, Urea). For the TS, time is

considered as 0 at time of diagnosis and then reported

as number of days from diagnosis. Data on all TSs

before diagnosis was discarded and z-normalization

was conducted on all values in the TSs before calcu-

lating distances. This was done for each E

element

separately, i.e. each TS then has values that have been

normalised across all patients for that particular E

to achieve mean equal to 0 and unit variance. Also,

we cleaned the data by discarding blood tests where

there was mostly missing data for all patients, and re-

moved patients which appeared to hold invalid val-

ues for some attributes, etc. At the end of this stage,

we still had 1,598 patient objects with SD for 26 at-

tributes and 22 distinct TSs.

5.2 A Worked Example

To understand how our approach applies to data, we

select a small sample of 16 patients that represent the

following scenarios:

S1 4 patients, O

: O

, that are described as complete

heterogeneous objects, with 22 TSs and SD ele-

ment with 26 recorded values. Manual examina-

tion of the raw data indicated they are very similar

(but not identical) in all of their elements. Thus,

we are certain that they are similar.

S2 4 patients, O

: O

, that are described as complete

heterogeneous objects, with 22 TSs and SD el-

ement with 26 recorded values. Manual exam-

ination of the raw data shows they are dissimi-

lar, and all their DMs reported concordant large

values (associated with dissimilarity). Thus, we

are certain that they are dissimilar according to all

their elements.

S3 The same 4 patients in S1 are used with some of

their elements discarded to create uncertainty, O

. They all hold a complete SD element but

are described by different number of TSs as we

have removed some. The no. of present TSs are

=14, O

=16, O

=13 and O

=15. Thus, they

are similar but we are uncertain as the objects are

incomplete.

S4 O

: O

, the same 4 patients in S2 but with some

added noise to the raw data so that they reported

large but divergent similarity according to the dif-

ferent DMs. Also we discarded some of the TSs

so the no. of TSs present are: O

=15, O

=16,

=17 and O

=12. Thus, they are dissimilar but

we are uncertain as disagreement and objects’ in-

completeness are present.

Note that in the process of removing TSs, we some-

times deleted the same TS element, E

TSi

, from two

objects and other times we discarded different TSs,

TSi

and E

TSj

, in order to test both cases.

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

274

Figure 2: FM for the data sample (A, to the left) and its

combined uncertainty ﬁlter (B, to the right). The uncer-

tainty ﬁlter reports the average of UFM and DFM. In A,

dark blue reﬂects strong similarity (FM≤0.1) and then it

scales through green until it reaches bright yellow to reﬂect

dissimilarity (FM=0.9). In B, the scales of grey colour re-

port uncertainty, the darker the colour the higher the level of

uncertainty. The white area in B supports the FM calcula-

tions for S

and S

cases with combined uncertainty values

≤ 0.05. The other calculations are subject to varying levels

of uncertainty.

Patients in the sample were compared to each

other following our SMF approach. Objects in S1 re-

ported similarity values in the FM < 0.2 while the

FM similarities for patients in S2 were > 0.7. Both

had all associated variance values, DFM, ≤ 0.1 and

incompleteness values, UFM, equal to 0. Patients in

S3 reported similarity values in FM < 0.2 with vari-

ances reported in DFM ≤ 0.2 and incompleteness val-

ues in UFM > 0.4. Patients in S4 reported similarity

values > 0.7 in FM with variances in DFM > 0.2 and

incompleteness in UFM > 0.4.

Figure 2 provides a visulisation of our results for

the small sample of data whereas Figure 3 gives the

FM visualisation for the entire patient dataset. In Fig-

ure 2 the UFM and DFM are used to report uncer-

tainty in the right hand heatmap (coloured in grey).

We can see in the heatmap on the right that patients

from S1 and S2 are similar/dissimilar respectively but

in both cases the similarity reported in the FM is cer-

tain according to the companion uncertainty heatmap.

On the other hand, patients in S3 are still similar (as

they related to S1 patients) but report higher levels of

uncertainty, whereas the S4 patients are both dissimi-

lar (as they relate to S2) and uncertain.

In Figure3 the heatmap on (A) represents FM sim-

ilarities for the whole dataset and in (B) the same FM

is presented but this time using uncertainty thresholds.

In this case, the companion UFM and DFM values are

used to highlight patients (coloured in grey) where

uncertainty is above predetermined thresholds. Any

value in the FM associated with a UFM value < 0.4%

or a DFM > 0.1 is coloured in grey.

Figure 3: FMs for the cancer heterogeneous dataset before

(A) and after (B) using a combined uncertainty ﬁlter that

sets the thresholds for UFM=0.4 and DFM=0.1. In A, dark

blue reﬂects strong similarity (FM≤0.09) and then it scales

through green until it reaches bright yellow to reﬂect dis-

similarity (FM=0.9. The same applies in B, in addition to

having the grey colour to represent all patients that report

uncertain distance values in FM due to exceeding one or

both of the determined thresholds.

6 CONCLUSIONS

We have deﬁned heterogeneous datasets as those de-

scribing complex objects comprising of several data

categories including structured data, images, free text,

time series and others. The analysis of such complex

data is one of the biggest challenges facing pattern

analysis tasks, yet few efforts have been devoted to

reaching a mature understanding of this problem. In

this research we propose an intermediary fusion ap-

proach, SFM, which produces a matrix of distances

for complex objects enabling the application of stan-

dard clustering algorithms. SMF aggregates partial

distances that we compute separately on each data

element. We enhance our approach by considering

uncertainty and providing separate measures of the

uncertainty involved both with missing elements and

with diverging distance measures.

We have proposed a very general approach which

can be applied to any problem where objects are de-

scribed by different data types corresponding to dif-

ferent elements or views of the same object. Provid-

ing suitable measures of distance can be found and

used to produce a normalised DM for each element,

such DMs can be fused with others using our ap-

proach. This intermediate fusion allows for the appli-

cation of standard clustering algorithms on the fused

distances. However, clustering results may be en-

hanced by modifying the clustering algorithm to take

accoung of the information contained in the compan-

ion matrices that describe uncertainty.

We provide some preliminary experimental appli-

cation to a real dataset of prostate cancer patients de-

ﬁned by both standard data and a number of TSs rep-

resenting blood test results. We show a worked exam-

ple of distance and uncertainty calculations and show

AFusionApproachtoComputingDistanceforHeterogeneousData

275

how the values may be visualised via heatmaps.

Further research would be required to fully evalu-

ate our approach and provide results including those

generated by clustering data using our fused dis-

tances. We will also need to compare our interme-

diary fusion approach with a late fusion approach us-

ing an ensemble clustering algorithm to perform the

clustering of complex objects.

REFERENCES

Berndt, D. J. and Clifford, J. (1996). Finding patterns in

time series: A dynamic programming approach. In

Fayyad, U. M., Piatetsky-Shapiro, G., Smyth, P., and

Uthurusamy, R., editors, Advances in Knowledge Dis-

covery and Data Mining, pages 229–248. American

Association for Artiﬁcial Intelligence, Menlo Park,

CA, USA.

Bettencourt-Silva, J., Iglesia, B. D. L., Donell, S., and

Rayward-Smith, V. (2011). On creating a patient-

centric database from multiple hospital information

systems in a national health service secondary care

setting. Methods of Information in Medicine, pages

6730–6737.

Bostr

om, H., Andler, S. F., Brohede, M., Johansson, R.,

Karlsson, A., van Laere, J., Niklasson, L., Nilsson,

M., Persson, A., and Ziemke, T. (2007). On the deﬁni-

tion of information fusion as a ﬁeld of research. Tech-

nical report, Institutionen f

or kommunikation och in-

formation.

Cormode, G. and McGregor, A. (2008). Approximation al-

gorithms for clustering uncertain data. In Proceed-

ings of the Twenty-seventh ACM SIGMOD-SIGACT-

SIGART Symposium on Principles of Database Sys-

tems, PODS ’08, pages 191–200, New York, NY,

USA. ACM.

Dimitriadou, E., Weingessel, A., and Hornik, K. (2002). A

combination scheme for fuzzy clustering. In Pal, N.

and Sugeno, M., editors, Advances in Soft Computing

AFSS 2002, volume 2275 of Lecture Notes in Com-

puter Science, pages 332–338. Springer Berlin Hei-

delberg.

Evrim, Rasmussen, M. A., Savorani, F., Ns, T., and Bro,

R. (2013). Understanding data fusion within the

framework of coupled matrix and tensor factoriza-

tions. Chemometrics and Intelligent Laboratory Sys-

tems, 129(9):53–63.

Goh, C. (1996). Representing and reasoning about semantic

conﬂicts. In In Heterogeneous Information System,

PhD Thesis, MIT.

Greene, D. and Cunningham, P. (2009). A matrix factoriza-

tion approach for integrating multiple data views. In

Buntine, W., Grobelnik, M., Mladeni, D., and Shawe-

Taylor, J., editors, Machine Learning and Knowl-

edge Discovery in Databases, volume 5781 of Lecture

Notes in Computer Science, pages 423–438. Springer

Berlin Heidelberg.

Henniger, O. and Muller, S. (2007). Effects of time normal-

ization on the accuracy of dynamic time warping. In

Biometrics: Theory, Applications, and Systems, 2007.

BTAS 2007. First IEEE International Conference on,

pages 1–6.

Jain, A. K., Murty, M. N., and Flynn, P. J. (1999). Data

clustering: A review. ACM Comput. Surv., 31(3):264–

323.

Kim, W. and Seo, J. (1991). Classifying schematic and data

heterogeneity in multidatabase systems. Computer,

24(12):12–18.

Laney, D. (2001). 3D data management: Controlling data

volume, velocity, and variety. Technical report, META

Group.

Long, B., Zhang, Z., Wu, X., and Yu, P. S. (2006). Spec-

tral clustering for multi-type relational data. In ICML,

pages 585–592.

Ma, H., Yang, H., Lyu, M. R., and King, I. (2008).

Sorec: Social recommendation using probabilistic

matrix factorization. In Proceedings of the 17th ACM

Conference on Information and Knowledge Manage-

ment, CIKM ’08, pages 931–940, New York, NY,

USA. ACM.

Maragos, P., Gros, P., Katsamanis, A., and Papandreou,

G. (2008). Cross-modal integration for performance

improving in multimedia: A review. In Maragos,

P., Potamianos, A., and Gros, P., editors, Multimodal

Processing and Interaction, volume 33 of Multimedia

Systems and Applications, pages 1–46. Springer US.

Pavlidis, P., Cai, J., Weston, J., and Noble, W. S. (2002).

Learning gene functional classiﬁcations from multi-

ple data types. Journal of Computational Biology,

9(2):401–411.

Ratanamahatana, C. A. and Keogh, E. (2005). Three myths

about dynamic time warping data mining. Proceed-

ings of SIAM International Conference on Data Min-

ing (SDM05), pages 506–510.

Skillicorn, D. B. (2007). Understanding Complex Datasets:

Data Mining with Matrix Decompositions. Chapman

and Hall/CRC, Taylor and Francis Group.

Strehl, A. and Ghosh, J. (2003). Cluster ensembles — a

knowledge reuse framework for combining multiple

partitions. J. Mach. Learn. Res., 3:583–617.

Zitnik, M. and Zupan, B. (2014). Matrix factorization-based

data fusion for gene function prediction in baker’s

yeast and slime mold. Systems Biomedicine, 2:1–7.

van Vliet, M. H., Horlings, H. M., van de Vijver, M. J.,

Reinders, M. J. T., and Wessels, L. F. A. (2012). In-

tegration of clinical and gene expression data has a

synergetic effect on predicting breast cancer outcome.

PLoS ONE, 7(7):e40358.

Yu, S., Falck, T., Daemen, A., Tranchevent, L.-C., Suykens,

J., De Moor, B., and Moreau, Y. (2010). L2-norm mul-

tiple kernel learning and its application to biomedical

data fusion. BMC Bioinformatics, 11(1).

Zeng, H.-J., Chen, Z., and Ma, W.-Y. (2002). A uniﬁed

framework for clustering heterogeneous web objects.

In Web Information Systems Engineering, 2002. WISE

2002. Proceedings of the Third International Confer-

ence, pages 161–170.

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

276