
The Helmet Fit Index
A Method for the Computational Analysis of Fit between Human Head Shapes and
Bicycle Helmets
Thierry Perret-Ellena, Aleksandar Subic, Toh Yen Pang and Helmy Mustafa
RMIT University, School of Aerospace, Mechanical And Manufacturing Engineering, Building 251, Level 3 Bundoora
Campus East, Plenty Road Bundoora Vic 3083,
Melbourne, Australia
Keywords: 3D Anthropometry, Reverse Engineering, Gap Analysis, Bicycle Helmet Fit, 3D Scanner.
Abstract: While a bicycle helmet protects the wearer’s head in the event of a crash, not every user benefits to the same
extent when wearing the headgear. A proper fit with the cyclist’s head is found to be one of the most
important attributes to improve protection during impact. A correct fit is defined as a small and uniform
distance between the helmet liner and the wearer’s head shape, with a broad coverage of the head area. The
scientific community has recognised the need for improved fitting, but in-depth methods to analyse and
compare the fit performance of distinct helmets models are still absent from the literature. We present a
method based on 3D anthropometry, reverse engineering techniques and computational analysis to redress
this shortcoming. As a result of this study, we introduce the Helmet Fit Index (HFI) as a tool for fit analysis
between a helmet model and a human head. It is envisaged that the HFI can provide detailed understanding
of helmet efficiency regarding fit and should be used during helmet development phases and testing.
1 INTRODUCTION
Bicycle helmets play an important role in cyclist
safety during crashes (Attewell et al., 2001); (Abu-
Zidan et al., 2007); (Cripton et al., 2014), where they
reduce the risk of head and facial injury significantly
across the whole cyclist population (Thompson et
al., 1999). However, studies showed that a poor
helmet fit on the wearer’s head may decrease its
safety benefits during a crash event (Romanow et
al., 2014) (Rivara et al., 1999).
Poor helmet fit may be attributed in two ways.
First, the helmet could be worn incorrectly, titled
either forward or backward, with the chin strap
unfastened or, with the helmet worn back to front.
An observational study from Canada reported that
15% of bike users worn their helmet incorrectly
(Hagel et al., 2010). Wearing under or over-sized
helmets is also considered as inappropriate usage.
Second, helmet sizes and shapes available to the
public might not be suitable for the full diversity of
head morphologies. Indeed, for some users there is
either a large gap between the inner liner and the
head, or a low coverage of the skull area with
significant unprotected regions on the head. Rivara
et al. (1999) found that during crash events, children
with head injuries had large open gaps between their
head and the helmet, compared to those without
head injuries.
While the misuse of bicycle helmets is rectifiable
through school-based education programs,
government and helmet manufacturer advertising,
and store advice and information, the mismatch
between head shapes and helmet liners seems to be
related to the design of helmets.
Nowadays, protective equipment are designed
and tested on standard mannequin heads called
headforms (Ball, 2009) (Zhuang et al., 2010), which
aim to represent the full range of head dimensions,
geometries and shapes within a population.
Although two headform standards have been
proposed in the past (ISO/R1511:1970 and ISO/DIS
6220:1983), neither of them were adopted as an
international standard. However, the draft ISO/DIS
6220:1983 has become a consensus international
standard for many countries and served as a
reference for the development of their own standard.
For instance, Australia developed the AS/NZS
2512.1:2009 Methods of testing protective helmets
Part 1: Definitions and headforms (Standards
Australia, 2009), where five headform sizes are
presented, namely A, E, J, M and O. Interestingly,
145
Perret-Ellena T., Subic A., Yen Pang T. and Mustafa H..
The Helmet Fit Index - A Method for the Computational Analysis of Fit between Human Head Shapes and Bicycle Helmets.
DOI: 10.5220/0005084101450153
In Proceedings of the 2nd International Congress on Sports Sciences Research and Technology Support (icSPORTS-2014), pages 145-153
ISBN: 978-989-758-057-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

the ISO draft was itself founded from the first set of
test headforms produced by the UK Transport Road
Research Laboratory in the 1950s’ (British
Standards Institution, 2006). One may think that
designing bicycle helmets on anthropometric
measurements from the 1950s British workforce
would not fully encompass the variability on head
shapes in today’s population. It might lead to
improper helmet fit for a large proportion of cyclists.
In order to go beyond the errors in the
anthropometric data and to match the majority of
people head shapes, designers have been creating
helmet liners with significant offset distance from
the standard headform surfaces. This designing
approach also ensures the highest proportions of
users are captured with the smallest numbers of
sizes. It is common for helmet manufacturers to only
provide one or two sizes for both male and female
populations. Thick foam pads are then added to fill
the gaps between the liners and wearer’s head.
While this approach noticeably improves comfort
and allows a minimum gap for air circulation, it does
not reduce front-to front, side-to-side, or rotational
movements that are responsible for poor helmet
fitting. It is apparent that such an approach leads to
improper helmet fit for a large range of consumers.
Even with a widely recognised poor head-fitted
bicycle helmet design (Robinette and Whitestone,
1994), accurate techniques to quantify the adequacy
or inadequacy of fit for a distinct person and a
distinct helmet are still tedious and inaccurate, and
are not in line with today’s technology. The distance
between the inside of the helmet and the skull of the
user is measured using depth probes through holes
drilled in the helmet. Only recently 3D scanners
have been introduced to accurately compute standoff
distances of ballistic helmets (Meunier et al., 2000).
The paper aims to present a method of estimating
the ‘fit score’ of bicycle helmets for unique human
head shapes. Based on 3D anthropometric studies, a
set of reverse engineering tools and computational
techniques was developed to evaluate the fit from
the combination of one helmet and one individual’s
head. We introduced the Helmet Fit Index (HFI) that
can be used for statistical analysis of fit on a defined
population and the comparison of different headgear
models.
2 METHOD
The helmet fit analysis method consisted of four
distinct steps: (1) Anthropometry data of participants
were recorded and processed using a handheld or
rotating 3D scanner and post processing software,
(2) bicycle helmets were digitised using a higher-
end, fixed 3D scanner, which generated scans with
greater accuracy and resolution, (3) both scans were
positioned in relation to a third intermediary 3D
scan, and (4) multiple computational analyses were
performed to compute the HFI for each participant.
2.1 3D Anthropometry: Data
Collection and Processing
The Artec Eva™ 3D scanner was used for the
anthropometric study. As a handheld white light
scanner, it can produce accurate point clouds up to
one hundred micrometres at a half a millimetre
resolution. It is completely portable and utilises
surface geometry and texture algorithms to align
itself in space and therefore does not require any
targets to be placed on the scanned area.
During the scanning process, participants were
asked to sit straight and look at a fixed point on the
wall with his/her usual facial expression. The
posture position and scanning techniques were in
accordance with the requirements of ISO
20685:2010(E) 3-D scanning methodologies for
internationally compatible anthropometric
databases (International Organization for
Standardization, 2010b). Participants were asked to
wear standard wig caps on their heads and over their
ears to avoid hair irregularities on the scanned
geometry. The scanner can record single scan at a
rate of fifteen frames per second for about thirty
seconds and automatically aligned the frames while
scanning (Figure 1(a)).
Figure 1: (a) Rough alignment of 532 single scans, (b)
Watertight scan.
Fine alignment algorithms and clean-up were
then performed on the individual shots before the
hundreds of scans were merged together in a smooth
(a) (b)
icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport
146
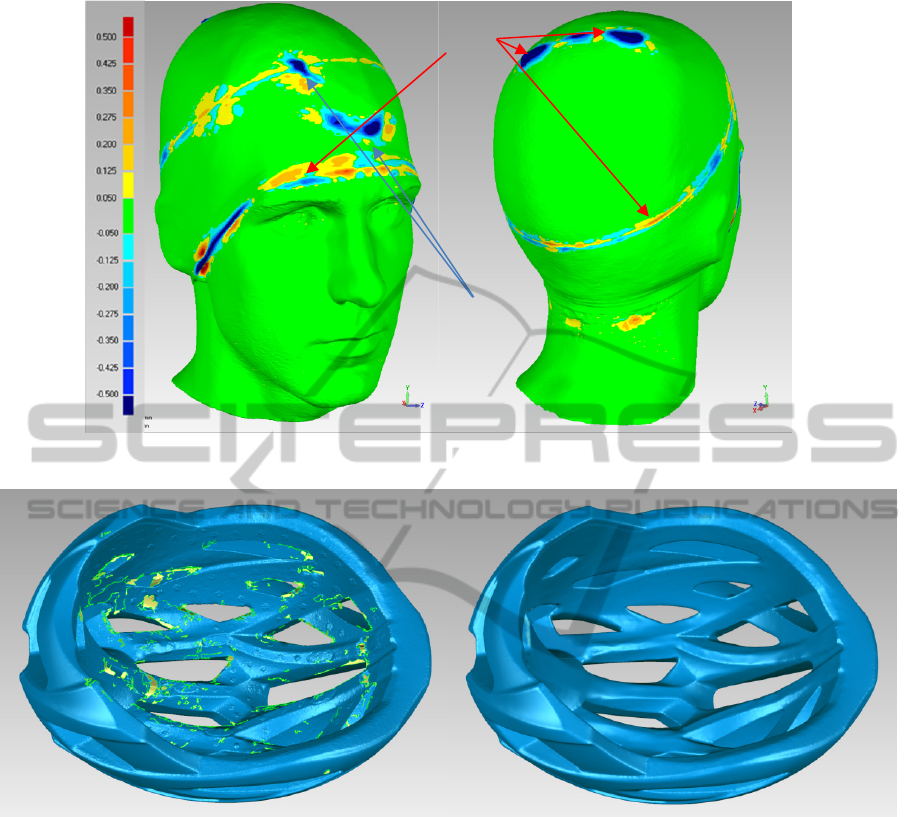
Figure 2: Deviation Analysis. Green is within the allowed distance variation.
Figure 3: Met Kaos size M. Left: Merged scans with holes, Right: Final helmet mesh (holes filled, repaired, smoothed out,
re-wrapped).
fusion procedure. Mesh was generated and missing
areas were filled to create a single watertight scan as
presented in Figure 1(b).
Mesh was then exported to Geomagic Studio 12
®
for further processing. Hair bumps and fabric folds
were removed while the scan was smoothed out by
minimising angles between individual polygons. The
deviation analysis tool was used to ensure that the
modification to the mesh had not excessively
distorted the original scanned head shape. The
maximum deviation distance for non-hair bumps or
fabric fold areas was set to 50μ. Figure 2 shows
the deviation analysis computed after the post
processing has been completed. The green areas are
deviation within the threshold value. Higher
deviation values (highlighted in red and blue) arose
from folds in the wig cap fabric and uneven surfaces
due to hair irregularities.
2.2 Bicycle Helmet Reverse
Engineering and Data Preparation
The tested helmet was digitised with an advanced
3D scanner (HDI Advance from LMI Technologies),
which has a high level of scan accuracy and quality
when dealing with more complex geometries. The
average point-to-point resolution is 75μ with an
accuracy of up to 45μ. Seventy single scans on
average were recorded for each helmet. Foam pads
and the adjusting system were removed either (i)
TheHelmetFitIndex-AMethodfortheComputationalAnalysisofFitbetweenHumanHeadShapesandBicycleHelmets
147

physically before the scan, or (ii) digitally during the
post processing procedure. The scan images were
merged, repaired and cleaned-up in Geomagic studio
12
®
(Figure 3 shows a scanned Met Kaos helmet
model). The clean-up process involved the
following: (a) repaired the mesh to remove spikes
and non-manifold triangles, (b) filled holes with
curvature continuity constraints with the adjacent
geometry, (c) reconstructed the fillets and sharp
edges, and (d) re-wrapped the mesh with new
vertices for uniform spacing. The final repaired
mesh produced approximately two million triangles.
When performing the gap analysis on the inside
surfaces of the helmet liner, we duplicated the mesh
on the software tree and kept only the regions
supposedly in contact with the cyclists’ head. Figure
4 illustrates the final inside surface of the same
helmet after careful trim and with proper area
selection.
Figure 4: Met Kaos, inside mesh.
The fit analysis was performed both globally and
locally as we predicted the fit to be dissimilar
throughout the whole head shape. The inside mesh
of the helmet liner was therefore further divided into
five regions, namely front, top, right, left, and back
as shown in figure 5.
2.3 Scans Alignment
In order to analyse the gap between the head and the
inside surface of the helmet liner, the fine helmet
mesh was assembled in position with the head scan.
Instead of manually aligning the two meshes
together, we utilised a third–intermediary scan to
properly position the helmet with the participant’s
head. Participants were scanned a second time with
the tested helmet model fitted on their heads. During
the scan, participants were asked to reproduce the
same posture and facial expression as the first scan
Figure 5: Met Kaos regions. green = front, pink = top, blue
= right, turquoise = left, yellow = back.
while a rough scan was performed. Foam pads, chin
strap and the adjusting system were excluded during
the fitting process as we only aimed to investigate
how well the helmet liner matched with the head
shape of the participant.
All three scans (Figure 6) were then aligned
using the n-points manual registration and the global
registration algorithms within Geomagic Studio 12
®
.
The alignment process was split into two stages: (i)
aligned the head scan and the intermediary scan
(Figure 7) using the face polygons of the participant,
and (ii) aligned the helmet scan with the
intermediary scan (Figure 8).
Figure 6: Three scans for alignment. Yellow: head scan.
Blue: Intermediary scan. Orange: Helmet scan.
Figure 7: Head/intermediary scan alignment. From left to
right: Face polygons selection for global registration (red),
good overlapping between the meshes, deviation analysis
(green is < to ±0.1mm).
icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport
148

Figure 8: Intermediary/helmet scan alignment. From left to
right: Helmet polygons selection for global registration
(red), good overlapping between the meshes, deviation
analysis (green is < to ±0.2mm).
After the two-stage alignment process, the
intermediary scan was removed, and the head and
helmet scans were now aligned accurately (Figure
9). This allowed the gap between the head and
helmet to be inspected and analysed.
Figure 9: Final alignment.
2.4 Gap Analysis
In this analysis, the gap distribution between the
head mesh and the inside of the helmet was
calculated. Two parameters were determined: (i) the
Standoff Distance (SOD), which was defined as the
average minimal distance to the head shape amongst
all the points that defined the inside mesh of the
liner, and (ii) the Gap Uniformity (GU), which was
the standard deviation of the gap distribution, and
defined as the dispersion from the average.
Figure 11: Gap analysis on the right region, and the SOD
and GU were 6.11mm and 1.84mm, respectively.
A distance analysis tool from CATIA V5R21
(Dassault Système) was used to measure the gap
between the trimmed head and the inside liner
meshes. We first analysed the gap to look for any
negative values that would indicate a crush between
the two meshes. Interference might arise either from
inaccurate alignment between the meshes, or the hair
Figure 10: Gap analysis texture maps before (interferences marked in red circle) and after offset. Hair thickness was
0.62mm, and SOD and GU were 5.98mm and 2.92mm, respectively.
TheHelmetFitIndex-AMethodfortheComputationalAnalysisofFitbetweenHumanHeadShapesandBicycleHelmets
149

thickness of the participant. The participant’s hair
was likely to be compressed under the helmet’s
weight during the fitting and this extra thickness of
hair was considered during the gap analysis.
Outliner points were removed from the result and
the head scan was offset by the negative maximum
deviation. The hair thickness was assumed to be
uniform across the whole head. Distance analysis
was then recalculated and the SOD and GU were
recorded. Figure 10 shows the gap analysis with
colour texture maps before and after the hair
thickness was offset.
Furthermore, similar deviation analyses were
conducted on the five local regions, and the SOD
and GU were recorded. Figure 11 depicts a gap
analysis of the right region.
2.5 Proportion of Head under Helmet
Protection
Ideally, the helmet should cover as much skull area
as possible to provide maximum protection to the
wearer. However, for some human head shapes,
helmet models might provide only minimal total
coverage area and put the wearer at increased risk of
injury. The AS/NZS 2512.1:2009 Methods of testing
protective helmets Part 1: Definitions and
headforms (Standards Australia, 2009) defines a test
line around the head where the helmet is supposed to
extend. The dimensions for the test line were based
on the Bitragion coronal and inion arcs, and the mid-
sagittal arc. We added the dimensions of the head
length, breadth and circumference to define, for each
participant, an area that should be under the helmet
protection (magenta area in Figure 12(a)).
By projecting the boundary edges of the inside
liner into the test area, we could compute the
proportion of the head mesh under helmet protection
(green area in Figure 12(b)). We named this third fit
parameter the Head Protection Proportion (HPP).
Figure 12: (a) Test area in magenta, (b) Actual helmet
protection area in green.
2.6 Helmet Fit Index
The Helmet Fit Index (HFI) aims to provide a fit
‘score’ for the combination of one specific helmet
model and a human head. This index was developed
on a scale from 0 (excessively poor fit) to 100
(perfect fit). The probability density function, , of
an exponential distribution was used to generate the
index was described as:
;
∗exp0,
0 0.
(1)
Where 0 was the parameter of the
distribution called the rate parameter.
The probability density function was established
on the exponential distribution rather than the log-
normal distribution as its right tail is relatively short
and may be considered as having moderate skew
(i.e. few outliners). A distribution with fewer
outliners will produce more statistical significant
results.
was defined as a function of the SOD, GU, and
HPP. It tends to approach 0 when the fit is
improved.
The SOD optimal value should be greater than
zero to allow thermal control throughout the helmet
and the addition of thin foam paddings for comfort.
However, previous research showed that an
excessive standoff distance would decrease the
helmet protective function during crashes (Rivara et
al., 1999). Therefore, we set the SOD to be optimum
when it ranged between 4 and 8mm.
The GU was a key parameter when analysing the
dispersion of the distance distribution. Seemingly,
the fit is optimised when the standoff distance is
uniformly distributed over the whole liner surface,
which equivalent to a lower deviation from the
mean. Hence, the gap becomes more uniform when
the GU gets closer to zero. Likewise, fit improves
when the HPP becomes closer to 1, which
corresponding to a higher coverage area of the head
provided by the helmet.
The fit parameter, , was defined as:
∗
|
6
|
2
∗
48
∗
48
(2)
Where and were calculated as coefficient
parameters. They provided more importance to GU
and HPP when computing the HFI.
2
3
6
5
, respectively.
Based on the observations for from twenty
(a)
(b
icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport
150

participants of this study, and some test results
published for 1D anthropometric studies using 1
st
and 99
th
percentile head measurements of females
and males, respectively from different ethnic groups
(Zhuang and Bradtmiller, 2005); (International
Organization for Standardization, 2010a), we
anticipated that would rarely exceed the 30 mark
and would represent an extremely low fit. We,
therefore, decided to assign 0.1 to and multiplied
the function by 1000 to define the function as
shown Figure 13 (e.g. with 30, 5).
:
0;∞
→
0;100
↦100∗exp0.1
(3)
Replacing in (3) and rounded up to 2 decimal
points gives:
100∗exp0.13
|
6
|
15
0.12
48
100∗exp
0.12
48
(4)
Similarly, a HFI score was developed for local
regions based only on the local SOD and GU. The
proposed equation was:
100∗exp0.13
|
6
|
15
0.12
48
100∗exp
0.12
48
(5)
Figure 13: HFI graph.
Table 1: Overall fit parameter values for 20 participants.
No.
Gender
Helmet
Size
Hair
Thickness
SOD
GU
Test
Area
Actual
Helmet
Protection
Area
HPP
HFI
1 Male Medium 3.35 6.76 3.40 66190 56610 0.855 4.8
62.1
2 Male Large 0.11 15.61 7.60 76670 46530 0.607 20.1
13.4
3 Female Medium 3.36 11.06 4.34 62150 50680 0.815 8.5
42.9
4 Male Large 3.22 10.50 4.36 70400 56350 0.800 8.2
43.9
5 Male Medium 3.79 9.17 4.11 66820 52570 0.787 7.1
49.3
6 Male Medium 4.46 8.11 2.98 68840 54830 0.796 4.6
63.2
7 Female Large 9.22 16.94 7.34 63640 55320 0.869 16.1
19.9
8 Male Large 1.44 9.58 4.68 63240 53980 0.854 7.7
46.5
9 Male Large 3.74 12.02 4.64 63140 54920 0.870 9.1
40.2
10 Male Medium 4.36 7.73 3.31 62430 54680 0.876 4.5
63.5
11 Male Large 2.88 9.28 3.67 72060 56265 0.781 6.5
52.1
12 Female Medium 4.41 8.97 3.48 63170 54340 0.860 5.5
57.5
13 Male Large 1.22 9.07 3.70 62740 54590 0.870 5.8
55.7
14 Male Medium 2.04 7.41 3.33 67190 53700 0.799 5.0
60.7
15 Male Large 7.62 14.17 5.18 67420 56733 0.841 11.5
31.6
16 Female Medium 2.98 10.37 5.55 54030 51140 0.947 8.6
42.1
17 Male Medium 2.88 7.12 3.59 75030 53415 0.712 6.1
54.6
18 Female Medium 7.35 10.17 3.74 64680 57100 0.883 6.6
51.9
19 Male Medium 5.96 5.98 2.92 72780 53640 0.737 4.8
62.1
20 Male Medium 4.10 10.96 5.09 61450 51430 0.837 9.3
39.4
Mean
3.92 10.05 4.35 66204 53941 0.820 8.0
47.6
Standard Deviation
2.23 2.88 1.30 5342 2543 0.074 4.0
14.0
0
20
40
60
80
100
0 102030405060
f(x)=HFI
x
TheHelmetFitIndex-AMethodfortheComputationalAnalysisofFitbetweenHumanHeadShapesandBicycleHelmets
151

3 RESULTS
Participants were 15 males and 5 females, aged
between 21 to 37 years (mean = 26.2 ± 4.5), took
part in the pilot study to evaluate the feasibility of
the method, and the performance and strength of the
HFIs. The participants were asked to try and select
the best perceived helmet fit between two sizes of
the same model (Met Kaos size Medium and Large)
before the start of the experiment. Table 1 presents
the results for the computed hair thickness, SOD,
GU, HPP, and HFI for each participant. The
parameters means and standard deviations are
presented in the last two rows of Table 1.
Fit parameters for the five local regions are
presented in table 2 with respective SODs, GUs and
HFIs.
4 DISCUSSION
The global HFI distribution from Table 1 shows two
extreme poor fit for participant No. 2 and No. 7
(HFI=13.4 and 19.9 respectively) with large SODs
and Gus. Only 60.7% of the head test area for
participant No. 2 was protected by the helmet. The
other 18 HFIs ranged from 31.6 to 63.5 with a mean
value of 47.6 (±14.0). It is apparent from Table 1
that the GUs are large, indicating a non-uniform
distribution of the gap throughout the head length.
Local gap distribution showed slight
dissimilarities between the five regions, with the
back region providing the bigger gaps (SOD) and a
worst fit (HFI) than the other helmet regions.
Further analysis with larger samples in both
number of participants and helmet models is deemed
necessary to establish the validity of these
observations. The pilot study will help in the
determination of the sample size for future helmet fit
analyses involving the HFI.
An exponential distribution is believed to have a
better impact on the index strength rather than a
linear distribution. It gives less amplitude to very
poor fit ~15) and more dissimilarity to small
variation when gets closer to zero. For this reason,
Table 2: Local fit parameter values for 20 participants.
No.
Front Top Right Left Back
SOD
(mm)
GU
(mm)
HFI
SOD
(mm)
GU
(mm)
HFI
SOD
(mm)
GU
(mm)
HFI
SOD
(mm)
GU
(mm)
HFI
SOD
(mm)
GU
(mm)
HFI
1 5.04 2.31
75.8
8.27 3.29
66.0
6.23 3.15
68.5
6.03 3.36
66.8
9.20 3.18
62.8
2 6.50 4.29
59.8
23.31 5.84
17.8
17.44 5.42
27.7
15.12 4.69
35.3
9.73 4.30
53.0
3 12.03 4.62
43.8
7.19 4.62
57.4
12.25 2.31
56.9
13.19 2.82
50.3
10.73 3.96
51.7
4 7.98 4.18
60.6
9.67 4.83
49.9
9.94 2.56
64.4
12.84 3.78
45.9
13.55 4.50
40.1
5 13.39 2.67
50.5
6.47 3.63
64.7
8.61 3.51
62.8
8.59 2.75
68.9
11.24 4.69
45.7
6 8.24 2.66
71.3
7.35 4.17
60.6
8.94 2.62
68.4
8.45 1.68
79.1
6.93 2.48
74.3
7 15.81 4.31
35.3
11.95 6.47
35.2
17.23 5.73
27.1
18.75 7.04
20.9
27.14 6.47
12.8
8 9.09 4.19
56.1
7.93 4.16
60.7
8.68 3.61
61.8
10.28 4.32
51.0
16.34 2.81
40.8
9 9.55 3.90
56.3
9.13 5.34
48.7
13.72 2.96
47.7
13.61 3.35
45.9
15.83 3.77
37.6
10 7.99 2.23
76.5
6.86 3.94
62.3
8.00 3.11
68.9
6.91 2.90
70.6
10.78 2.54
61.1
11 8.42 4.49
56.5
8.54 4.61
55.3
9.66 2.60
65.3
10.34 2.88
60.4
9.99 2.63
63.7
12 12.57 2.61
53.7
7.47 4.00
61.9
8.82 2.63
68.8
8.48 2.04
75.6
8.01 3.85
62.8
13 9.41 3.07
62.8
7.31 4.60
57.6
8.78 2.30
71.8
9.91 3.51
57.6
12.18 3.03
52.4
14 7.49 3.50
65.7
7.21 3.70
64.1
8.95 2.00
73.6
6.96 3.08
69.1
5.13 3.61
64.8
15 15.52 2.79
43.2
9.81 4.89
49.1
14.84 4.25
37.9
14.19 3.92
41.2
21.77 3.52
26.1
16 15.46 2.93
42.6
6.66 3.80
63.4
8.84 4.58
54.4
8.69 4.12
58.1
18.48 3.06
34.3
17 10.42 2.65
61.7
8.16 3.75
62.9
5.97 3.34
67.0
4.86 2.52
73.9
7.39 1.82
80.4
18 9.12 2.57
67.9
8.00 4.24
60.1
11.37 2.89
56.3
10.68 2.6
61.0
13.14 2.73
51.0
19 5.66 2.90
70.6
6.03 3.74
63.8
6.11 1.84
80.2
7.05 2.13
77.4
3.60 3.07
67.1
20 16.39 2.86
40.4
8.44 3.37
64.6
9.28 4.02
56.5
8.76 3.42
62.9
17.15 2.09
42.1
ME
10.30 3.29
57.6
8.79 4.35
56.3
10.18 3.27
59.3
10.18 3.35
58.6
12.42 3.41
51.2
SD
3.50 0.80
12.1
3.68 0.82
11.8
3.34 1.07
14.4
3.49 1.17
15.3
5.75 1.06
16.7
icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport
152

we decided to base the HFI on the exponential
distribution rather than the value.
We acknowledged there were some limitations
for the presented method. First, we assumed that the
participants’ hair were fully flattened under the
helmet compression and did not affect the fit score.
While this might be the case for most cyclists, HFI
for people with very thick, bulky and curly hair will
produce erroneous results. Also, a uniform hair
thickness across the participant’s head might not be
accurate. People with some baldness may only have
hair on the side of the head, while others may have
asymmetric haircuts with non-uniform hair
distribution.
Despite the limitations, our findings showed that
the HFI method did provide accurate and efficient
data to analyse, compare and improve bicycle
helmet fit amongst the cyclist population considered.
Further studies are however required to gather
deeper insights on the HFI prospective.
5 CONCLUSIONS
The paper focuses on bicycle helmet fit that closely
influences the wearer’s safety during crashes
involving head impact. A computational analysis
method has been developed to help quantifying how
closely the contour of a helmet liner follows the
head shape of an individual. The HFI was introduced
and found to be a plausible accurate tool for fit
analysis. Such information was relevant and useful
and might be taken into consideration in both helmet
development and testing.
This study is part of a larger project emphasising
on helmet comfort and safety assessment from
random sampling of the Australian cycling
community. It aims at improving helmet fit and
hence safety through mass-customisation.
REFERENCES
Abu-Zidan, F. M., Nagelkerke, N. & Rao, S. 2007. Factors
Affecting Severity Of Bicycle-Related Injuries: The
Role Of Helmets In Preventing Head Injuries. Emerg
Med Australas, 19, 366-71.
Attewell, R. G., Glase, K. & Mcfadden, M. 2001. Bicycle
Helmet Efficacy A Meta-Analysis. Accident Analysis
And Prevention, 33, 345-352.
Ball, R. 2009. 3-D Design Tools From The Sizechina
Project. Ergonomics In Design: The Quarterly Of
Human Factors Applications, 17, 8-13.
British Standards Institution 2006. Bs En960:2006.
Headforms For Use In The Testing Of Protective
Helmets.
Cripton, P. A., Dressler, D. M., Stuart, C. A., Dennison, C.
R. & Richards, D. 2014. Bicycle Helmets Are Highly
Effective At Preventing Head Injury During Head
Impact: Head-Form Accelerations And Injury Criteria
For Helmeted And Unhelmeted Impacts. Accid Anal
Prev, 70c, 1-7.
Hagel, B. E., Lee, R. S., Karkhaneh, M., Voaklander, D. &
Rowe, B. H. 2010. Factors Associated With Incorrect
Bicycle Helmet Use. Inj Prev, 16, 178-84.
International Organization For Standardization 2010a.
Iso7250-2 Basic Human Body Measurements For
Technological Design,.
International Organization For Standardization 2010b. Iso
20685:2010(E) 3-D Scanning Methodologies For
Internationally Compatible Anthropometric Databases.
Meunier, P., Tack, D., Ricci, A., Bossi, L. & Harry, A.
2000. Helmet Accommodation Analysis Using 3d
Laser Scanning. Applied Ergonomics, 31, 361-369.
Rivara, F. P., Astley, S. J., Clarren, S. K., Thompson, D.
C. & Thompson, R. S. 1999. Fit Of Bicycle Safety
Helmets And Risk Of Head Injuries In Children.
Injury Prevention, 5, 4.
Robinette, K. M. & Whitestone, J. J. 1994. The Need For
Improved Anthropometric Methods For The
Development Of Helmet Systems. Aviation Space And
Environmental Medicine, 65, A95-A99.
Romanow, N. R., Hagel, B. E., Williamson, J. & Rowe, B.
H. 2014. Cyclist Head And Facial Injury Risk In
Relation To Helmet Fit: A Case-Control Study.
Chronic Diseases And Injuries In Canada, 34.
Standards Australia 2009. As/Nzs 2512.1:2009 Methods
Of Testing Protective Helmets Part 1: Definitions
And Headforms.
Thompson, D. C., Rivara, F. P. & Thompson, R. 1999.
Helmets For Preventing Head And Facial Injuries In
Bicyclists. Cochrane Database Syst. Rev.
Zhuang, Z., Benson, S. & Viscusi, D. 2010. Digital 3-D
Headforms With Facial Features Representative Of
The Current Us Workforce.
Ergonomics, 53, 661-71.
Zhuang, Z. & Bradtmiller, B. 2005. Head-And-Face
Anthropometric Survey Of U.S. Respirator Users. J
Occup Environ Hyg, 2, 567-76.
TheHelmetFitIndex-AMethodfortheComputationalAnalysisofFitbetweenHumanHeadShapesandBicycleHelmets
153
