Beat to Beat Estimation of cosRT Angle and cosRT RR Hysteresis from

Exercise ECG Measurement

Jukka A. Lipponen

1,2

and Mika P. Tarvainen

1,2

Department of Applied Physics, University of Eastern Finland, Kuopio, Finland

Department of Clinical Physiology and Nuclear Medicine, Kuopio University Hospital, Kuopio, Finland

Keywords:

Spatial QRS T-angle, Exercise ECG.

Abstract:

Method for estimating beat-by-beat cosRT angle from the 12-lead exercise electrocardiogram (ECG) measure-

ment is presented. Method uses principal component regression to generate ECG waveform model, and uses

this model to denoise QRS complexes and T-waves. In addition two different methods for synthetizing vector

ECG from the conventional 12-lead measurement are compared. First method synthetize vector ECG by using

inverse of the Dowers matrix and second method produces vector ECG by using singular value decomposition.

Results indicate that vector ECG synthesized using Dowers matrix gives more comparable results for healthy

subjects. Beat-by-beat cosRT estimation revealed that due to respiration angle values can vary as much as

70 degrees, because of changes to electrode positions and volume conduction model of the torso. Thereby

presented method for beat-by-beat estimation of the cosRT angle can improve reliability of this parameter.

1 INTRODUCTION

Exercise electrocardiogram (ECG) measurement has

been used decades as a clinical tool for detecting sev-

eral cardiac diseases such as ischemic heart disease.

Recent studies have shown that exercise measurement

can be also used for predicting sudden cardiac death

for general population and after myocardial infarc-

tion (Zabel et al., 2000; Kardys et al., 2003; Kentt¨a

et al., 2010; Kentt¨a et al., 2011). In addition cosRT

angle and its relation to heart rate during exercise has

been shown to have prognostic value (Kentt¨a et al.,

2012). cosRT angle has been shown to relate to heart

rate level, however this relation differs during exer-

cise and recovery periods i.e. cosRT angle return to-

wards the normal values slower than the heart rate.

This phenomenon is called as cosRT/RR hysteresis.

It is shown that cosRT RR relation is disrupted in pa-

tients with cardiac events (Kentt¨a et al., 2012).

The cosRT angle can be estimated from vec-

tor ECG (VECG) which is measured using Franks

lead conﬁguration. Thereby traditionally measured

12 lead ECG must be transformed to correspond

ECGx, ECGy and ECGz leads of VECG measure-

ment. There are two commonly used methods to syn-

thetize VECG leads from the 12 lead measurements.

First method is so called Dowers method were inverse

of the Dowers transformation matrix is used to pro-

duce x, y and z VECG leads (Dower et al., 1980;

Edenbrandt and Pahlm, 1988). Second possibility is

to use singular value decomposition (SVD) to pro-

duce three orthogonal ECG components from the 12

lead measurements. In this paper we compare these

two techniques to synthetize VECG components us-

ing three exercise ECG measurements and the beat-

by-beat cosRT angles estimated from ECGx, ECGy

and ECGz components produced by both methods are

compared.

The cosRT angle is traditionally estimated using

averaged beat epochs, but in this paper a method

for estimating cosRT angle beat-by-beat is presented.

Method uses principal component regression (PCR)

to generate ECG waveform model, and uses this

model to denoise QRS complex and T-wave epochs.

It is assumed that by using beat-by-beat estimates of

cosRT angle, its relation to heart rate can be better

characterized and abnormalities could be found more

reliably.

2 MATERIALS AND METHODS

2.1 Constructing x, y and z Leads

Before the VECG synthetization, baseline wander

A. Lipponen J. and P. Tarvainen M..

Beat to Beat Estimation of cosRT Angle and cosRT RR Hysteresis from Exercise ECG Measurement.

DOI: 10.5220/0005084900220026

In Proceedings of the 2nd International Congress on Cardiovascular Technologies (CARDIOTECHNIX-2014), pages 22-26

ISBN: 978-989-758-055-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

caused by chest movements were removed from the

ECG by applying a median ﬁlter in a 1 s long win-

dow and by subtracting the acquired baseline from the

original ECG. Secondly, EMG and power line noise

were reduced using a sixth order Butterworth low pass

ﬁlter with a cut-off frequency at 48 Hz.

In this study, two methods for synthesizing ECGx,

ECGy and ECGz leads from the conventional 12-lead

measurement were used. First method was Dow-

ers method where inverse of the Dowers transforma-

tion matrix is used to synthetize VECG leads (Dower

et al., 1980). Dowers matrix is based on the Franks

torso model and was created for achieving 12-lead

ECG diagnostics from the Frank VECG recordings

(Dower et al., 1980; Edenbrandt and Pahlm, 1988).

Synthetized leads produced by Dowers method are

designated here as ECGx

dow

,ECGy

dow

and ECGz

dow

Second option for synthetizing three independent

leads from the conventional 12-lead ECG is singular

value decomposition (Acar and Koymen, 1999). The

idea in using the SVD algorithm is to produce three

orthogonal ECG components, rather than approxima-

tion of the Frank lead system. In SVD, ECG data ma-

trix Z, the rows of which contain the 8 independent

leads of the 12-lead ECG is decomposed into three

individual matrixes:

Z = UΣV where, UU

= VV

= I (1)

U and V matrixes are orthonormal and they are gen-

erally called as left and right singular matrixes. Af-

ter the SVD decomposition, ﬁrst three components

(eigenvectors) of the left singular matrix U are used

as VECG components. Properties of SVD method en-

sures that ﬁrst component contains most of the energy

of ECG and second component most of the remaining

energy under the restriction of orthogonality to the

ﬁrst component. First three orthogonal components

are used for cosRT estimation and are designated here

as ECGx

svd

, ECGy

svd

and ECGz

svd

3 PCR MODELING OF ECG

After the construction of the ECGx, ECGy and ECGz

leads, the R-waves were detected using an adaptive

QRS detector (Tarvainen et al., 2014). Secondly PCR

modeling was used to improve signal to noise ratio.

Idea of the PCR modeling is to collect QRS com-

plexes and T-wave epochs to individual data matrixes

and create data driven model for QRS complex and

T-wave epochs. Here basic principles of this method

are presented, for more detailed description see (Lip-

ponen et al., 2013; Lipponen et al., 2010).

First QRS complexes and T-waves must be ex-

tracted from all VECG leads (ECGx, ECGy and

ECGz). Because QRS-complex duration is rather

constant regardless of the heart rate, QRS-complexes

can be extracted using constant window. T-wave du-

ration on the other hand is highly related to heart rate

and thus dynamic window is used for T-wave extrac-

tion.

QRS

= [−0.1, 0.1] s



0.1,



(2)

were R-wave ﬁducial points are used as a zero point

(t=0) and RR is the mean RR interval length. Next,

modeling of the (i:th) wave epoch (z

) is presented,

similar procedure is used for all QRS complex and T-

wave epochs in the ECGx, ECGy and ECGz channels.

1 Collect 50 previousand 50 following wave epochs

to measurement matrix Z

Z = [z

i−50

, z

i−49

, . . . z

i+49

, z

i+50

]

2 Construct four most signiﬁcant PCR basis vectors,

which are eigenvectors (v

) of the data correlation

matrix (R)

R =

100

= λv

3 Use PCR basis vectors for modeling epoch z

= Hθ+ e

where H = [v

, v

4 LS solution for the model parameters

= H

5 Modeled wave epoch is estimated as

= H

Model basis vector must be estimated dynami-

cally because during exercise increase of the heart rate

causes changes to position and shape of the T-wave.

By using 50 previous and 50 following wave epochs

heart rate changes does not disrupt the model basis

vectors and sufﬁcient prior information is achieved.

Four most signiﬁcant PCR basis vector are capable to

model individual waveform and its normal variation

and random noise is left out for less signiﬁcant basis

vectors.

4 cosRT ESTIMATION

cosRT angle estimation was performed in beat-by-

beat manner directly from the PCR-modelled QRS

and T-wave epochs. By using PCR modeling SNR

of the ECG can be increased such that beat-by-beat

detection of the cosRT angle is possible. cosRT an-

gle is deﬁned as the cosine of the dominant vectors

BeattoBeatEstimationofcosRTAngleandcosRTRRHysteresisfromExerciseECGMeasurement

Frontal Horizontal Sagittal

Dower

Exercise

Dower

Baseline

SVD

Exercise

SVD

Baseline

ECGy

svd

ECGx

svd

ECGz

svd

−2 0 2 4

−4

−2

ECGx

svd

ECGy

svd

−2 0 2 4

−1

ECGx

svd

ECGz

svd

−4 −2 0

−1

ECGy

svd

ECGz

svd

ECGy

svd

ECGx

svd

ECGz

svd

0 2 4 6

−4

−2

ECGx

svd

ECGy

svd

0 2 4 6

−1

ECGx

svd

ECGz

svd

−4 −2 0 2

−1

ECGy

svd

ECGz

svd

ECGy

dow

ECGx

dow

ECGz

dow

−200 0 200 400

−200

200

ECGx

dow

(mV)

ECGy

dow

(mV)

−200 0 200 400

100

200

ECGx

dow

(mV)

ECGz

dow

(mV)

−200 0 200

100

200

ECGy

dow

(mV)

ECGz

dow

(mV)

ECGy

dow

ECGx

dow

ECGz

dow

0 200 400 600

−100

100

200

300

ECGx

dow

(mV)

ECGy

dow

(mV)

0 200 400 600

−200

200

ECGx

dow

(mV)

ECGz

dow

(mV)

−100 0 100 200 300

−200

200

ECGy

dow

(mV)

ECGz

dow

(mV)

Figure 1: Examples of vector loops constructed by using inverse of the Dowers matrix and SVD. First row and second row

vector loops are estimated using inverse of the Dowers matrix. First row presents VECG loops during the baseline period and

second during the exercise period. Similarly vector loops produced by SVD are presented in third and fourth rows.

(80% of the maximum value) of the QRS vector loop

and the main vector of the T-wave loop. Its value is

limited in the range [-1,1] where -1 reﬂects the sit-

uation where vector loops are pointing at the oppo-

site directions and 1 reﬂects the situation where the

loops are pointing at the same direction. cosRT an-

gles estimated from the VECG synthetized by using

Dower’s method are designated as cosRT

dow

and sim-

ilarly cosRT angles estimated from the components

produced by SVD are designated as cosRT

svd

4.1 Measurements

Presented methods were tested using three different

incremental exercise tests on cycloergometer. Three

healthy male subjects participated to the measure-

ments. Measurements were performed by using a

Cardiovit CS-200 ergospirometer system (Schiller

AG). ECG electrodes were placed according to the

conventional 12-lead system with the MasonLikar

modiﬁcation. Sample rate of the ECG was 500Hz.

In the measurement, subject ﬁrst lay supine for 3 min,

and then sat up on the bicycle for the next 3 min. Af-

ter this bicycle load was initially set to 40W and the

load was increased with 40W every 3 min. Subject

continued exercise until exhaustion. After the subject

indicated that he could not go on anymore, the exer-

cise test was stopped and a 10 min recovery period

was measured.

5 RESULTS

Figure 1 presents examples of the vector loops con-

structed by using inverse of the Dower’s matrix and

SVD before and during the exercise. From the vector

loops constructed by Dowers inverse matrix, it can be

seen that during exercise QRS dominant vector shifts

towards the S-wave part of the QRS loop. This sifting

is clearly visible at least in horizontal and sagittal pro-

jections. T-wave loop direction remains rather con-

stant during the whole measurement. From the SVD

synthetized vector loops similar sifting is clearly vis-

ible at the projection of second and third component

CARDIOTECHNIX2014-InternationalCongressonCardiovascularTechnologies

0.4

0.6

0.8

−1

cosRT

dow

0 10 20

−1

time (s)

cosRT

svd

0 10 20 30

time (s)

0 10 20 30

time (s)

Figure 2: Estimated time series from all three subjects. First row presents RR interval time series in dark gray and used load

in light gray ﬁll. Second and third row presents estimated beat-to-beat time series of the cosRT angles. In second row, angle

is calculated from the vector loops constructed by Dowers inverse matrix and in third row cosRT is estimated from the SVD

synthetized vector loops. Trend of each time series is peresened as red line.

(ECGy and ECGz), however also loop morphology

changes signiﬁcantly caused by the changes in the

third (least signiﬁcant) SVD component.

In ﬁgure 2 beat-to-beat time series of RR-interval

and cosRT angles are presented for all three subjects.

cosRT

dow

seems to behave rather similarly for all sub-

ject, it decreases along the heart rate and after the ex-

ercise it slowly returns towards baseline. cosRT

svd

behavior is also rather similar as cosRT

dow

although

in third subject there can be seen small increase at the

end of the exercise period.

Figure 3 presents cosRT changes as a function of

the RR-interval during exercise and recovery periods.

cosRT values were divided into a bins according to

coincident RR-interval, used bins were [0.35 0.4 . . .

0.85] s and mean ± standard deviation of each bin

is presented in the ﬁgure 3, during the exercise using

red line and using blue line for the values estimated

during the recovery period. cosRT

dow

/RR hysteresis

is clearly visible in all three subjects. cosRT

dow

re-

turns towards the normal values slower than the heart

rate and mean values of the cosRT

dow

bins forms nice

hysteresis curve. cosRT

svd

on the other hand does not

form as clear hysteresis curve as cosRT

dow

, at least

in third subject cosRT

svd

values during the recovery

period are similar as during the exercise.

6 DISCUSSION

Beat-to-beat estimation method of the cosRT angle

from the standard 12-lead ECG measurement has

been presented. In addition cosRT angles deﬁned

from vector loops synthetized using two different

methods were compared. Results show that cosRT

changes during the exercise are more comparable be-

tween the subjects if Dowers inverse matrix is used

for VECG synthetization.

Earlier studies have shown that in SVD syn-

thetized VECG most of the signal energy is contained

in the ﬁrst two decomposed channels (Acar and Koy-

men, 1999). In third channel ECG power is low and

thus small changes in the potentials of the heart can

induce large morphological changes into this third

channel. This could lead to unexpected variation in

the cosRT

svd

angles. However it could be meaning-

ful to study if all relevant information of the cosRT

svd

can be captured using only the two most signiﬁcant

synthetized ECG leads.

Beat-to-beat variation of the cosRT angle is sig-

niﬁcant, as can be seen in ﬁgure 2. Variation dur-

ing intense exercise can be as large as 70 degrees and

this variation is most likely caused by respiration. In

cosRT time series respiration rhythm is clearly visible

in all parts of the measurement. Respiration causes

changes into the electrode positioning with respect to

the heart (due to chest movements), but also it causes

continuous changes to the characteristics of the

BeattoBeatEstimationofcosRTAngleandcosRTRRHysteresisfromExerciseECGMeasurement

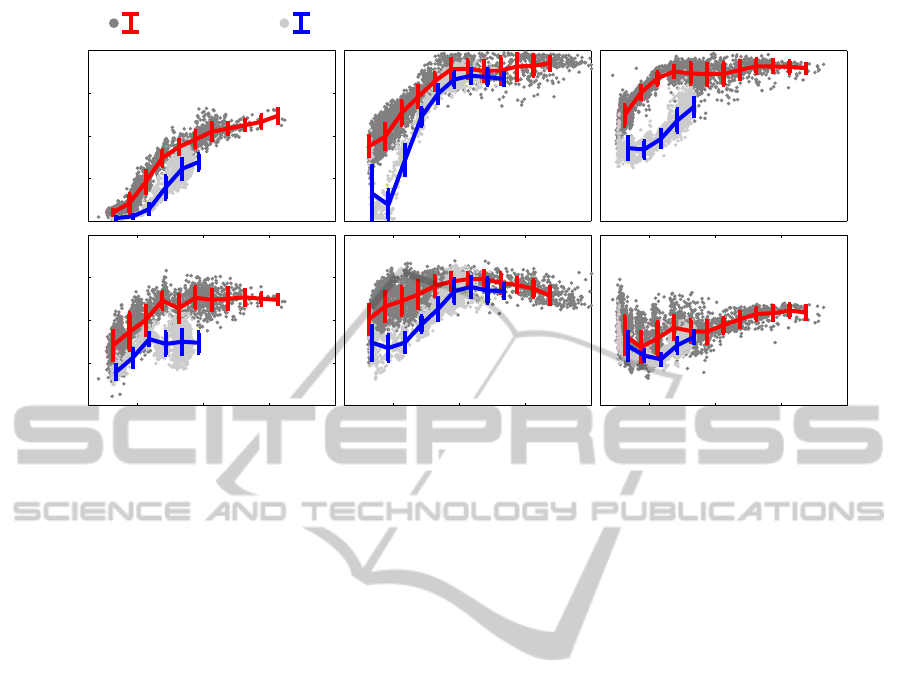
Exercise Recovery

0.4 0.6 0.8 1

−1

−0.5

0.5

RR (s)

cosRT

svd

0.4 0.6 0.8 1

RR (s)

0.4 0.6 0.8 1

RR (s)

−1

−0.5

0.5

cosRT

dow

Figure 3: cosRT changes as a function of the RR-intercal during exercise and recovery periods are presented for all three

subjects. First row presents cosRT

dow

angles and second row cosRT

svd

angles. Estimated angle values during exercise are

marked as dark gray and during recovery period as light gray. cosRT values were divided into bins depending on current

RR-interval, mean±SD during exercise are shown in red and during recovery in blue lines.

torso’s volume conduction model. Both of these is-

sues cause changes into the ECG components and to

the estimated cosRT angles. Beat-by-beat estimation

methods are important, because the effects of respira-

tion can be better observed and when necessary can

be taken into account in the analysis, and thereby, the

reliability of the VECG parameters such as the cosRT

angle could be improved.

ACKNOWLEDGEMENTS

Study was supported by Kuopio University Hospital

VTR grant.

REFERENCES

Acar, B. and Koymen, H. (1999). Svd-based on-line exer-

cise ecg signal orthogonalization. Biomedical Engi-

neering, 46:311–321.

Dower, G., Machado, H., and Osborne, J. (1980). On de-

riving the electrocardiogram from vectoradiographic

leads. Clin Cardio, 3:87.

Edenbrandt, L. and Pahlm, O. (1988). Vectorcardiogram

synthesized from a 12-lead ecg: superiority of the

inverse dower matrix. Journal of electrocardiolog,

21:361–367.

Kardys, I., Kors, J. A., van der Meer, I. M., Hofman, A.,

van der Kuip, D. A., and Witteman, J. C. (2003). Spa-

tial qrs-t angle predicts cardiac death in a general pop-

ulation. European heart journal, 24:1357–1364.

Kentt¨a, T., Karsikas, M., J.Junttila, M., Perki¨om¨aki, J. S.,

Sepp¨anen, T., Kiviniemi, A., Nieminen, T., Lehtim¨aki,

T., Nikus, K., Lehtinen, R., Viik, J., K¨ah¨onen, M., and

Huikuri, H. V. (2011). Qrs-t morphology measured

from exercise electrocardiogram as a predictor of car-

diac mortality. Europace, 13:701–707.

Kentt¨a, T., Karsikas, M., Kiviniemi, A., Tulppo, M.,

Sepp¨anen, T., and Huikuri, H. V. (2010). Dynamics

and rate-dependence of the spatial angle between ven-

tricular depolarization and repolarization wave fronts

during exercise ecg. Annals of Noninvasive Electro-

cardiology, 15:264–275.

Kentt¨a, T., Viik, J., Karsikas, M., Sepp¨anen, T., Nieminen,

T., Lehtim¨aki, T., Nikus, K., Lehtinena, R., K¨ah¨onen,

M., and Huikuri, H. V. (2012). Postexercise recov-

ery of the spatial qrs/t angle as a predictor of sudden

cardiac death. Heart Rhythm, 9:1083–1089.

Lipponen, J. A., Gladwell, V. F., Kinnunen, H., Karjalainen,

P. A., and Tarvainen, M. P. (2013). The correlation of

vectorcardiographic changes to blood lactate concen-

tration during an exercise test. Signal Processing and

Control, 8:491–499.

Lipponen, J. A., Tarvainen, M. P., Laitinen, T., Lyyra-

Laitinen, T., and Karjalainen, P. A. (2010). A prin-

cipal component regression approach for estimation

of ventricular repolarization characteristics. Transac-

tions Biomedical Engineering, 57:1062–1069.

Tarvainen, M. P., Niskanen, J. P., Lipponen, J. A., Ranta-

Aho, P. O., and Karjalainen, P. A. (2014). Kubios

hrvheart rate variability analysis software. Computer

methods and programs in biomedicine, 113:210–220.

Zabel, M., Acar, B., Klingenheben, T., Franz, M. R., Hohn-

loser, S. H., and Malik, M. (2000). Analysis of 12-

lead t-wave morphology for risk stratiﬁcation after

myocardial infarction. Circulation, 102:1252–1257.

CARDIOTECHNIX2014-InternationalCongressonCardiovascularTechnologies