Studying and Tackling Noisy Fitness in Evolutionary Design of Game

Characters

J. J. Merelo

, Pedro A. Castillo

, Antonio Mora

, Antonio Fern

andez-Ares

Anna I. Esparcia-Alc

azar

, Carlos Cotta

and Nuria Rico

University of Granada, Department of Computer Architecture and Technology,

ETSIIT and CITIC, 18071 Granada, Spain

S2Grupo, Valencia, Spain

Universidad de M

alaga, Departamento de Lenguajes y Sistemas Inform

aticos, M

alaga, Spain

Universidad de Granada, Depto. Estad

ıstica e Investigaci

on Operativa, Granada, Spain

Keywords:

Evolutionary Algorithms, Noisy Optimization Problems, Games, Strategy Games.

Abstract:

In most computer games as in life, the outcome of a match is uncertain due to several reasons: the characters

or assets appear in different initial positions or the response of the player, even if programmed, is not deter-

ministic; different matches will yield different scores. That is a problem when optimizing a game-playing

engine: its ﬁtness will be noisy, and if we use an evolutionary algorithm it will have to deal with it. This is

not straightforward since there is an inherent uncertainty in the true value of the ﬁtness of an individual, or

rather whether one chromosome is better than another, thus making it preferable for selection. Several meth-

ods based on implicit or explicit average or changes in the selection of individuals for the next generation have

been proposed in the past, but they involve a substantial redesign of the algorithm and the software used to

solve the problem. In this paper we propose new methods based on incremental computation (memory-based)

or ﬁtness average or, additionally, using statistical tests to impose a partial order on the population; this partial

order is considered to assign a ﬁtness value to every individual which can be used straightforwardly in any se-

lection function. Tests using several hard combinatorial optimization problems show that, despite an increased

computation time with respect to the other methods, both memory-based methods have a higher success rate

than implicit averaging methods that do not use memory; however, there is not a clear advantage in success

rate or algorithmic terms of one method over the other.

1 INTRODUCTION

In our research on the optimization of the behavior

of bots or game strategies, we have frequently found

that the ﬁtness of a bot is noisy, in the sense that re-

peated evaluations will yield different values (Mora

et al., 2012) which is a problem since ﬁtness is the

measure used to select individuals for reproduction.

If we look at in in a more general setting, noise in the

ﬁtness of individuals in the context of an evolution-

ary algorithm has different origins. It can be inher-

ent to the individual that is evaluated; for instance, in

(Mora et al., 2012) a game-playing bot (autonomous

agent) that includes a set of application rates is op-

timized. This results in different actions in different

runs, and obviously different success rates and then

ﬁtness. Even comparisons with other individuals can

be affected: given exactly the same pair of individu-

als, the chance of one beating the other can vary in

a wide range. In other cases like the one presented

in the MADE environment, where whole worlds are

evolved (Garc

ıa-Ortega et al., 2014) the same kind

of noisy environment will happen. When using evo-

lutionary algorithms to optimize stochastic methods

such as neural networks (Castillo et al., 1999) us-

ing evolutionary algorithms the measure that is usu-

ally taken as ﬁtness, the success rate, will also be

noisy since different training schedules will result in

slightly different success rates.

The examples mentioned above are included ac-

tually in one or the four categories where uncertain-

ties in ﬁtness are found, ﬁtness functions with intrin-

sic noise. These four types include also, according

to (Jin and Branke, 2005) approximated ﬁtness func-

tions (originated by, for instance, surrogate models);

robust functions, where the main focus is in ﬁnding

Merelo J., Castillo P., Mora A., Fernández-Ares A., Esparcia-Alcázar A., Cotta C. and Rico N..

Studying and Tackling Noisy Fitness in Evolutionary Design of Game Characters.

DOI: 10.5220/0005085700760085

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 76-85

ISBN: 978-989-758-052-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

values with high tolerance to change in initial evalua-

tion conditions, and ﬁnally dynamic ﬁtness functions,

where the inherent value of the function changes with

time. Our main interest will be in the ﬁrst type, since

it is the one that we have actually met in the past and

which has led to the development of this work.

At any rate, in this paper we will not be dealing

with actual problems; we will try to simulate the ef-

fect of noise by adding to the ﬁtness function Gaus-

sian noise centered in 0 and σ = 1, 2, 4. We will

deal mainly with combinatorial optimization func-

tions with noise added having the same shape and

amplitude, that we actually have found in problems

so far. In fact, from the point of view of dealing with

ﬁtness, these are the main features of noise we will be

interested in.

The rest of the paper is organized as follows: next

we describe the state of the art in the treatment of

noise in ﬁtness functions. The method we propose

in this paper, called Wilcoxon Tournament, will be

shown in Section 4; experiments are described and

results shown in Section 5; ﬁnally its implications are

discussed in the last section of the paper.

2 STATE OF THE ART

The most comprehensive review of the state of the art

in evolutionary algorithms in uncertain environments

was done by Jin and Branke in 2005 (Jin and Branke,

2005), although recent papers such as (Qian et al.,

2013) include a brief update of the state of the art.

In that ﬁrst survey of evolutionary optimization by Jin

and Branke in uncertain environments this uncertainty

is categorized into noise, robustness, ﬁtness approxi-

mation and time-varying ﬁtness functions, and then,

different options for dealing with it are proposed. In

principle, the approach presented in this paper was de-

signed to deal with the ﬁrst kind of uncertainty, noise

in ﬁtness evaluation, although it could be argued that

there is uncertainty in the true ﬁtness as in the third

category. In any case it could be applied to other types

of noise. In this situation, several solutions were been

proposed and explained in the survey (Jin and Branke,

2005). These will be explained next.

An usual approach is just disregard the fact that

the ﬁtness is noisy and using whatever value is re-

turned a single time or after re-evaluation each gen-

eration. This was the option in our previous research

in games and evolution of neural networks (Castillo

et al., 1999; Mora et al., 2010; Merelo-Guerv

os et al.,

2001) and leads, if the population is large enough,

to an implicit averaging as mentioned in (Jin and

Branke, 2005). In fact, evolutionary algorithm selec-

tion is also stochastic, so noise in ﬁtness evaluation

will have the same effect as randomness in selection

or a higher mutation rate, which might make the evo-

lution process easier and not harder in some particular

cases (Qian et al., 2013). In fact, Miller and Goldberg

proved that an inﬁnite population would not be af-

fected by noise (Miller and Goldberg, 1996) and Jun-

Hua and Ming studied the effect of noise in conver-

gence rates (Jun-hua and Ming, 2013), proving that

an elitist genetic algorithm ﬁnds at least one solution

with a lowered convergence rate. But populations are

ﬁnite, so the usual approach is to increase the popula-

tion size to a value bigger than would be needed in a

non-noisy environment. This has also the advantage

that no special provision or change to the implemen-

tation has to be made; but a different value of a single

parameter.

Another more theoretically sound way is using a

statistical central tendency indicator, which is usually

the average. This strategy is called explicit averaging

by Jin and Branke and is used, for instance, in (Jun-

hua and Ming, 2013). Averaging decreases the vari-

ance of ﬁtness but the problem is that it is not clear in

advance what would be the sample size used for av-

eraging (Aizawa and Wah, 1994). Most authors use

several measures of ﬁtness for each new individual

(Costa et al., 2013), although other averaging strate-

gies have also been proposed, like averaging over the

neighbourhood of the individual or using resampling,

that is, more measures of ﬁtness in a number which is

decided heuristically (Liu et al., 2014). This assumes

that there is, effectively, an average of the ﬁtness val-

ues which is true for Gaussian random noise and other

distributions such as Gamma or Cauchy but not nec-

essarily for all distributions. To the best of our knowl-

edge, other measures like the median which might

be more adequate for certain noise models have not

been tested; the median always exists, while the aver-

age might not exist for non-centrally distributed vari-

ables. Besides, most models keep the number of eval-

uations is ﬁxed and independent of its value, which

might result in bad individuals being evaluated many

times before being discarded; some authors have pro-

posed resampling, that is, re-evaluate the individuals

a number of times to increase the precision in ﬁtness

(Rada-Vilela et al., 2014), which will effectively in-

crease the number of evaluations and thus slow down

the search. In any case, using average is also a small

change to the overall algorithm framework, requiring

only using as new ﬁtness function the average of sev-

eral evaluations. We will try to address this in the

model presented in this paper.

These two approaches that are focused on the eval-

uation process might be complemented with changes

StudyingandTacklingNoisyFitnessinEvolutionaryDesignofGameCharacters

to the selection process. For instance, using a thresh-

old (Rudolph, 2001) that is related to the noise char-

acteristics to avoid making comparisons of individ-

uals that might, in fact, be very similar or statisti-

cally the same; this is usually called threshold selec-

tion and can be applied either to explicit or implicit

averaging ﬁtness functions. The algorithms used for

solution, themselves, can be also tested, with some

authors proposing, instead of taking more measures,

testing different solvers (Cauwet et al., 2014), some

of which might be more affected by noise than others.

Any of these approaches do have the problem of

statistical representation of the true ﬁtness, even more

so if there is not such a thing, but several measures

that represent, all of them the ﬁtness of an individual.

This is what we are going to use in this paper, where

we present a method that uses resampling via an in-

dividual memory and use either explicit averaging or

statistical tests like the non-parametric Wilcoxon test.

First we will examine and try to ﬁnd the shape of

the noise that actually appears in games; then we will

check in this paper what is the inﬂuence on the qual-

ity of results of these two strategies and which one, if

any, is the best when working in noisy environments.

3 NOISE IN GAMES: AN

ANALYSIS

In order to measure the nature of noise, we are go-

ing to use the Planet Wars game, that has been used

as a framework for evolving strategies, for instance,

in (Mora et al., 2012). In this game, initial position

of the players is random with the constraint that they

should be far enough from each other; other than that,

any planet in the game can be an initial position. Be-

sides, in the strategy used in that game, actions are not

deterministic, since every player is deﬁned by a set of

probabilities to take one course of action.

An evolutionary algorithm with standard parame-

ters was run with the main objective of measuring the

behavior of ﬁtness. A sample of ten individuals from

generation 1, and another 10 from generation 50 were

extracted. The ﬁtness of each individual was mea-

sured 100 times. The main intention was also to see

how noise evolved with time. Intuitively we thought

that, since the players become better with evolution,

the noise and thus the standard deviation would de-

crease. However, what we found is plotted in Figure

1, which shows a plot of the standard deviation in both

generations and illustrates the fact that the spread of

ﬁtness values is bigger as the evolution proceeds, go-

ing from around 0.15 to around 0.20. which might be

a bit misleading since the average values of the ﬁtness

increase at the same time, but it implies that the noise

level might be around 20% of the signal in these kind

of problems.

But we were also interested in checking whether,

in fact, the normal distribution is the best ﬁt for the ﬁt-

ness measures. We tested three distributions: Gamma,

Weibull and normal (Gaussian) distribution after do-

ing an initial test that included Cauchy and Expo-

nential. All this analysis was done using the library

fitrdist in R, and data as well as scripts needed to

do it are publicly available. After trying to ﬁt these

three distribution to data in generation 1 and 50, we

analyzed goodness-of-ﬁt using the same package and

the gofstat function. This function yields several

measures of goodness, including the Akaike Informa-

tion Criterion and the Kolmogorov-Smirnov statistic.

What we found was that, in all cases, Gamma is

the distribution that better ﬁts the data. That does not

mean that the noise effectively follows this distribu-

tion, but that if it can be said to follow one, it’s this

one. In fact, just a few individuals have a good ﬁt (to

95% accuracy using the Kolmogorov-Smirnov), and

none of them in generation 50. The ﬁt for an individ-

ual in the ﬁrst generation that does follow that distri-

bution (individual 8) is shown in ﬁgure 2.

This ﬁgure also shows that, even if it is skewed,

its skewness is not too high which makes it close to

the standard distribution (which is considered a good

approximation if k ¿ 10).

Some interesting facts that can be deduced from

these measures is that in general, ﬁtness is skewed and

has a high value. Besides, it follows a gamma distri-

bution, which, if we wan to model noise accurately,

should be the one used. However, we are rather inter-

ested in the overall shape of noise so since the skew-

ness value of the gamma distribution is rather high we

will use, in this paper, a Gaussian noise to simulate it.

This will be used in the experiments shown below.

4 FITNESS MEMORY AND

STATISTICAL SIGNIFICANT

DIFFERENCES

As indicated in previous section, most explicit aver-

aging methods use several measures to compute ﬁt-

ness as an average, with resampling, that is, additional

measures, in case comparisons are not statistically

signiﬁcant. In this paper we will introduce a ﬁtness

memory, which amounts to a resampling every gen-

eration an individual survives. An individual is born

with a ﬁtness memory of a single value, with memory

size increasing with survival time. This is actually a

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

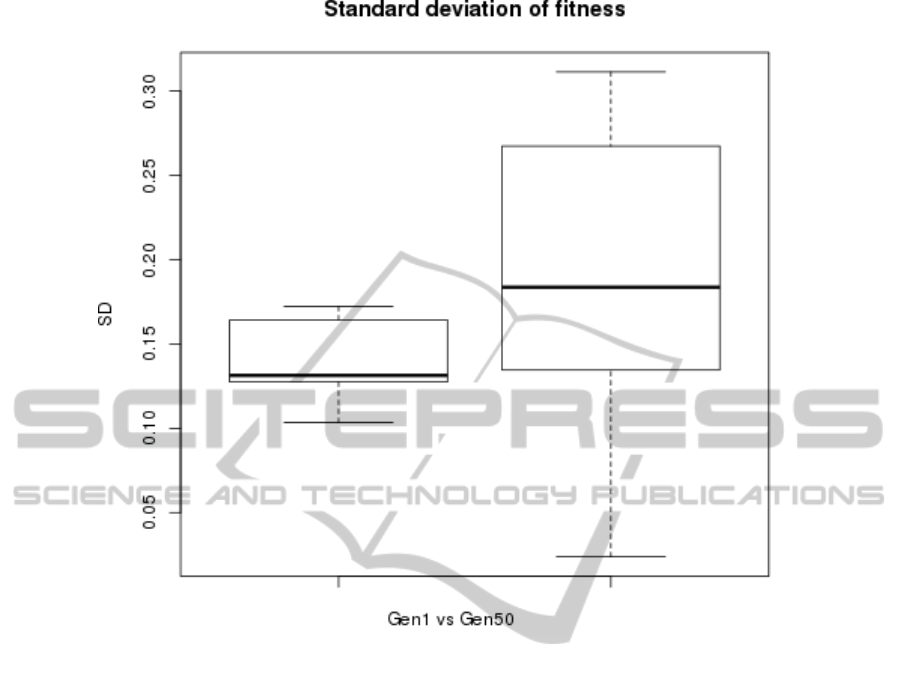
Figure 1: Boxplot of standard deviation of noise ﬁtted to a normal distribution, left for the ﬁrst generation and right for the

50th. Fitness averages around 1.

combination of an implicit and an explicit evaluation

strategy: younger individuals are rejected outright if

their ﬁtness computed after a single evaluation is not

enough to participate in the pool, while older ones use

several measures to compute average ﬁtness, which

means that averages will be a more precise represen-

tation of actual value. As evolution proceeds, the best

individuals will, effectively, have an underlying non-

noisy best value. We will call this method incremental

temporal average or ITA.

However, since average is a single value, selec-

tion methods might, in fact, select as better individ-

uals some that are not if the comparison is not sta-

tistically signiﬁcant; this will happen mainly in the

ﬁrst and middle stages of search, which might effec-

tively eliminate from the pool or not adequately rep-

resent individuals that constitute, in fact, good solu-

tions. That is why we introduce an additional feature:

using Wilcoxon test (Wilcoxon, 1945) for comparing

not the average, but all ﬁtness values attached to an

individual. This second method introduces a partial

order in the population pool: two individuals might

be different (one better than the other) or not. There

are many possible ways of introducing this partial or-

der in the evolutionary algorithm; however, what we

have done is to pair individuals a certain number of

times (10, by default) and have every individual score

a point every time it is better than the other in the cou-

ple; it will get a point less if it is the worse one. An

individual that is better that all its couples will have a

ﬁtness of 20; one whose comparisons are never signif-

icant according to the Wilcoxon test will score exactly

10, the same as if it wins as many times as it loses,

and the one that always loses will score 0. We will

call this method Wilcoxon-test based partial order, or

WPO for short.

Initial tests, programmed in Perl using

Algorithm::Evolutionary (Merelo-Guervs

et al., 2010) and available with an open source license

at http://git.io/a-e were made with these two types of

algorithms and the Trap function (Merelo-Guervs;,

2014), showing the best results for the WPO method

and both of them being better that the implicit

average method that uses a single evaluation per

individual, although they needed more time and

memory. Since it does not need to perform averages

StudyingandTacklingNoisyFitnessinEvolutionaryDesignofGameCharacters

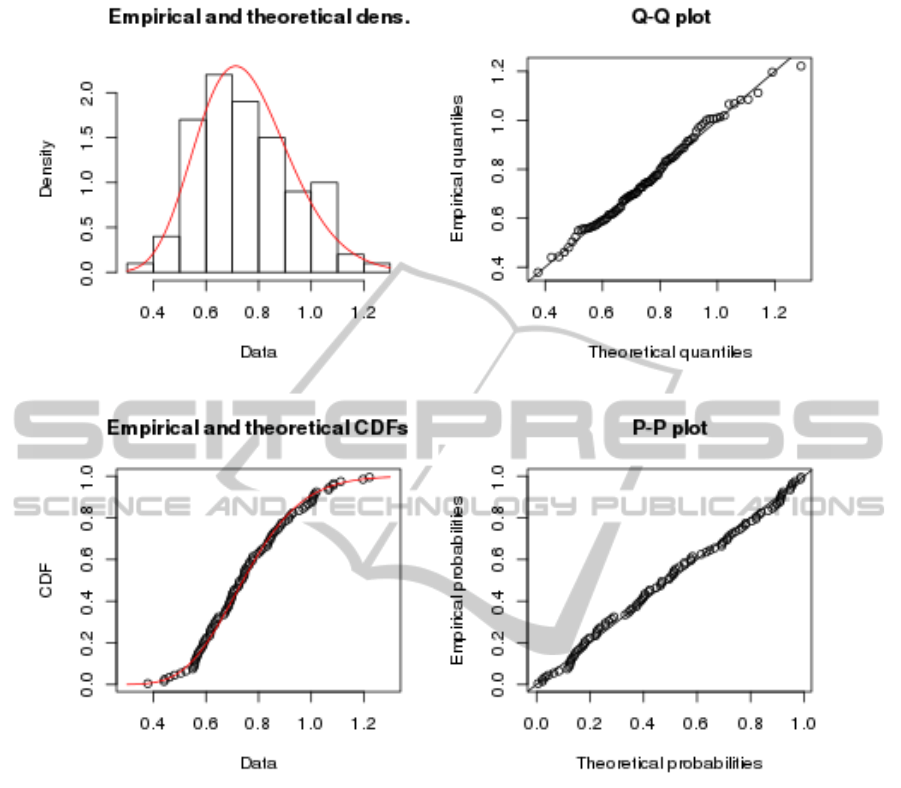
Figure 2: Fit of the ﬁtness value of an individual in the ﬁrst generation of the evolutionary algorithm to a gamma distribution,

showing an histogram in the top left corner, CDFs in the bottom left corner and quantile-quantile and percentile-percentile

plots in the right hand side.

or make additional ﬁtness measures every generation,

it is twice as fast as the next method, the one that uses

explicit average ﬁtness. An exploration of memory

sizes (published in http://jj.github.io/Algorithm-

Evolutionary/graphs/memory/ and shown in Figure 3

for a typical run) showed that they are distributed un-

evenly but, in general, there is no single memory size

overcoming all the population. Besides, distribution

of ﬁtness, published at http://jj.github.io/Algorithm-

Evolutionary/graphs/ﬁtness-histo/ shows a distribu-

tion with most values concentrated along the middle

(that is, ﬁtness equal to 10 or individuals that cannot

be compared with any other, together with a few

with the highest ﬁtness and many with the lowest

ﬁtness. Besides showing that using the partial order

for individual selection is a valid strategy, it also

shows that a too greedy selection method would

eliminate many individuals that might, in fact, have

a high ﬁtness. This will be taken into account

when assigning parameter values to the evolutionary

algorithm that will be presented next.

5 RESULTS

ITA and WPO have been tested using two well-known

benchmarks, the deceptive bimodal Trap (Deb and

Goldberg, 1992) function and the Massively Mul-

timodal Deceptive Problem (Goldberg et al., 1992)

(MMDP). We chose to use just these two functions

were chosen because they have different ﬁtness land-

scapes, are usually difﬁcult for an evolutionary algo-

rithm and have been extensively used for testing other

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

(a) Memory size (b) Fitness distribution

Figure 3: (Left) 3D plot of the distribution of memory sizes for a single execution of the Wilcoxon-test based partial order.

(Right) 3d plot of the distribution of ﬁtness values along time for the WPO method on the Trap function.

Table 1: Common evolutionary algorithm parameters.

Parameter Value

Chromosome length 40 (Trap) 60 (MMDP)

Population size 1024

Selection 2 tournament selection

Replacement rate 50%

Mutation rate 20%

Crossover rate 80%

Max evaluations 200K (Trap) 1 Million(MMDP)

Stopping criterion Non-noisy best found or max evaluations reached

kind of operators and algorithms.

Several methods were tested: a baseline algorithm

without noise to establish the time and number of

evaluations needed to ﬁnd the solution, a 0-memory

(implicit average) method that uses noisy ﬁtness with-

out making any special arrangement, ITA and WPO.

Evolutionary algorithm parameters and code for all

tests were the same, except in one particular case: we

used 2-tournament with 50% replacement, 20% muta-

tion and 80% crossover, p = 1024 and stopping when

the best was found or number of evaluations reached.

This was 200K for the Trap, which used 40 as chro-

mosome size, and 1M for MMDP, which used 60 as

chromosome size; these parameters are shown in Ta-

ble 1. We have also used an additive Gaussian noise

centered in zero and different σ, which is indepen-

dent of the range of variation of the ﬁtness values. By

default, noise will follow a normal distribution with

center in 0 and σ = 1.

All tests use the Algorithm::Evolutionary li-

brary, and the scripts are published, as above, in the

GitHub repository, together with raw and processed

results. The evolutionary algorithm code used in all

cases is exactly the same except for WPO, which,

since it needs the whole population to evaluate ﬁt-

ness, needed a special reproduction and replacement

library. This also means that the replacement method

is not exactly the same: while WPO replaces every

generation 50% of the individuals, the rest evaluate

new individuals before replacement and eliminate the

worst 512 (50% of the original population). Replace-

ment is, thus, less greedy in the WPO case, but we

do not think this will be a big inﬂuence on result

(although it might account for the bigger number of

evaluations obtained in some cases), besides, it just

needed a small modiﬁcation of code and was thus pre-

ferred for that reason. All values shown are the result

of 30 independent runs.

The results for different noise levels are shown in

Figure 4. The boxplot on the left hand side compares

the number of evaluations for the baseline method

and the three methods with σ = 1. The implicit av-

erage method (labelled as 0-memory) is only slightly

worse than the baseline value of around 12K evalua-

StudyingandTacklingNoisyFitnessinEvolutionaryDesignofGameCharacters

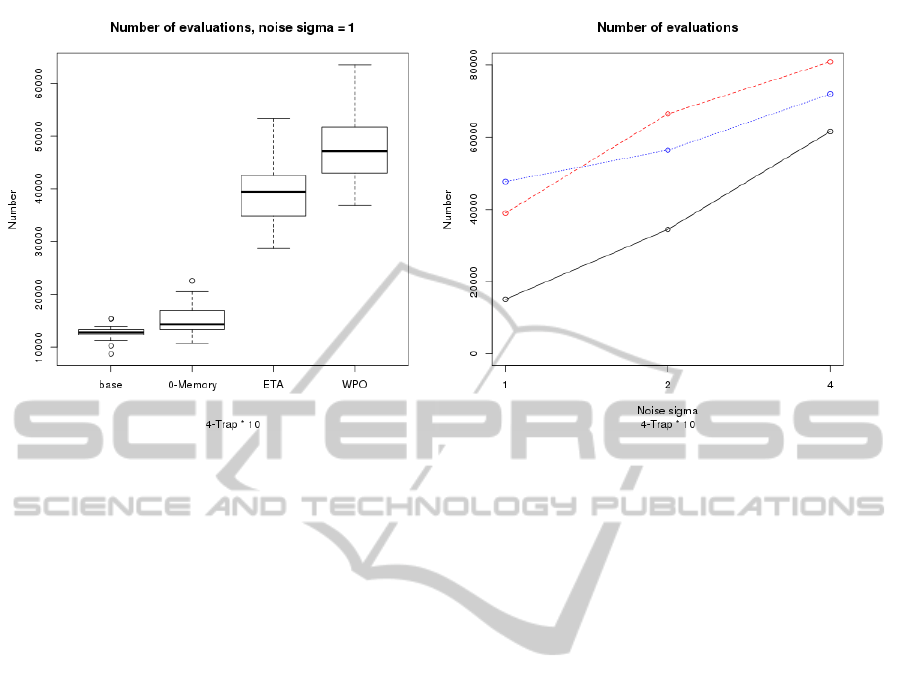
(a) Memory size (b) Fitness distribution

Figure 4: (Left) Comparison of number of evaluations for the 4-Trap x 10 function and the rest of the algorithms with a

noise σ equal to 1. (Right). Plot of average number of evaluations for different methods: 0 memory (black, solid), ITA (red,

dashed), WPO (blue, dot-dashed).

tions, with the ITA and WPO methods yielding very

similar values which are actually worse than the 0-

memory method. However, the scenario on the right,

which shows how the number of evaluations scales

with the noise level, is somewhat different. While the

0-memory method still has the smallest number of

evaluations for successful runs, the success rate de-

grades very fast, with roughly the same and slightly

less than 100% for σ = 2 but falling down to 63% for

0-memory and around 80% for ITA and WPO (86%

and 80%). That is, best success rate is shown by the

ITA method, but the best number of evaluations for

roughly the same method is achieved by WPO.

These results also show that performance de-

grades quickly with problem difﬁculty and the de-

gree of noise, that is why we discarded the 0-memory

method due to its high degree of failure (a high per-

centage of the runs did not ﬁnd the solution) with

noise = 10% max ﬁtness and evaluated ITA and WPO

over another problem, MMDP with similar absolute

σ, with the difference that, in this case, σ = 2 would

be 20% of the max value, which is close to the one

observed experimentally, as explained in the Section

The evolutionary algorithm for MMDP used ex-

actly the same parameters as for the Trap function

above, except the max number of evaluations, which

was boosted to one million. Initial tests with the 0-

memory method yielded a very low degree of suc-

cess, which left only the two methods analyzed in this

paper for testing with MMDP. Success level was in

all cases around 90% and very similar in all exper-

iments; the number of evaluations is more affected

by noise and shown in Figure 5. In fact, WPO and

ITA have a very similar number of evaluations. It is

statistically indistinguishable for σ = 2, and different

only at the 10% level (p-value = 0.09668) for σ = 1,

however, if we take the time needed to reach solu-

tions into account, ITA is much faster since it does

not apply 10*1024 statistical tests every generation.

However, WPO is more robust, with a lower standard

deviation, in general, at least for high noise levels.

However, both methods obtain a good result with a

much higher success rate than the implicit ﬁtness (0-

memory) method. Besides, ITA and APO incorporate

explicit ﬁtness evaluation naturally into the popula-

tion resampling only surviving individuals. This ac-

counts for a predictable behaviour of the algorithm,

since the number of evaluations per generation is ex-

actly the population size, which is important for opti-

mization processes with a limited budget.

6 CONCLUSIONS

In this paper we have introduced two methods to deal

with the problem of noisy ﬁtness functions. The two

methods, ITA, based on re-evaluation of surviving in-

dividuals and WPO, which uses the Wilcoxon test

to compare a sample of individuals and partial-order

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

Figure 5: Number of evaluations for successful runs ITA and WPO needed for solving the MMDP problem with 6 blocks and

different noise levels, σ = 1, 2.

them within the population, have been tested over two

different ﬁtness functions and compared with implicit

average (or 0-memory) methods, as well as among

themselves. In general, memory-based methods have

much higher success rate than 0-memory methods

and the difference increases with the noise level, with

0-memory methods crashing at noise levels close to

20% while ITA and WPO maintain a high success

level.

It is difﬁcult to choose between the two proposed

methods, ITA and WPO. However, ITA is much faster

since it avoids costly comparisons. It also has a

slightly higher success rate, and the number of eval-

uations it needs to ﬁnd the solution is only slightly

worse; even if from the point of view of the evolu-

tionary algorithm it is slightly less robust and slightly

worse, it compensates the time needed to make more

evaluations with the fact that it does not need to per-

form statistical tests to select new individuals.

However, this research is in initial stages. The fact

that we are using a centrally distributed noise gives

ITA an advantage since, in fact, comparing the mean

of two individuals will be essentially the same as do-

ing a statistical comparison, since when the number

of measures is enough, statistical signiﬁcance will be

reached. In fact, with a small difference ITA might

select as better an individual whose ﬁtness is actually

the same, something that would be correctly spotted

StudyingandTacklingNoisyFitnessinEvolutionaryDesignofGameCharacters

by WPO, but, in fact, since there is an average selec-

tive pressure this is not going to matter in the long

run.

It might matter in different situations, for instance

in numerical optimization problems and also when

noise follows an uniform distribution; behavior might

in this case be similar to when noise levels are higher.

These are scenarios that are left for future research,

and destined to ﬁnd out in which situations WPO is

better than ITA and the other way round.

Besides exploring noise in different problems and

modelling its distribution, we will explore different

parameters. The ﬁrst one is the number of compar-

isons in WPO. Initial explorations have proved that

changing it from 5 to 32 does not yield a signiﬁ-

cant difference. Looking for a way to speed up this

method would also be important since it would make

its performance closer to ITA. Memory size could also

be explored. Right now evaluations are always per-

formed, but in fact after a number of evaluations are

done comparisons will be statistically signiﬁcant; it

is difﬁcult to know, however, which is this number,

but in long runs it would be interesting to cap ﬁtness

memory size to a sensible number, or, in any case, see

the effect of doing it.

ACKNOWLEDGEMENTS

This work has been supported in part by project

ANYSELF (TIN2011-28627-C04-02 and -01). The

authors would like to thank the FEDER of Euro-

pean Union for ﬁnancial support via project ”Sistema

de Informacin y Prediccin de bajo coste y autnomo

para conocer el Estado de las Carreteras en tiempo

real mediante dispositivos distribuidos” (SIPEsCa) of

the ”Programa Operativo FEDER de Andaluca 2007-

2013”. We also thank all Agency of Public Works of

Andalusia Regional Government staff and researchers

for their dedication and professionalism.

Our research group is committed to Open Sci-

ence and the writing and development of this pa-

per has been carried out in GitHub at this address

https://github.com/JJ/wilcoxon-ga-ecta. We encour-

age you to visit, comment and to all kind of sugges-

tions.

Miller, B. L. and Goldberg, D. E. (1996). Ge-

netic algorithms, selection schemes, and the

varying eﬀects of noise. Evolutionary Com-

putation, 4(2):113–131.

Mora, A. M., Fern´andez-Ares, A., Guerv´os, J.

J. M., Garc´ıa-S´anchez, P., and Fernandes,

C. M. (2012). Eﬀect of noisy ﬁtness in real-

time strategy games player behaviour opti-

misation using evolutionary algorithms. J.

Comput. Sci. Technol., 27(5):1007–1023.

Mora, A. M., Montoya, R., Merelo, J. J., S´anchez,

P. G., Castillo, P. A., Laredo, J. L. J.,

Mart´ınez, A. I., and Espacia, A. (2010).

Evolving bot´s ai in unreal. In di Chio et

al., C., editor, Applications of Evolutionary

Computing, Part I, volume 6024 of Lecture

Notes in Computer Science, pages 170–179,

Istanbul, Turkey. Springer-Verlag.

Qian, C., Yu, Y., and Zhou, Z.-H. (2013). Ana-

lyzing evolutionary optimization in noisy en-

vironments. CoRR, abs/1311.4987.

Rada-Vilela, J., Johnston, M., and Zhang, M.

(2014). Population statistics for particle

swarm optimization: Resampling methods

in noisy optimization problems. Swarm and

Evolutionary Computation, 0(0):–. In press.

Rudolph, G. (2001). A partial order approach to

noisy ﬁtness functions. In Proceedings of the

IEEE Conference on Evolutionary Computa-

tion, ICEC, volume 1, pages 318–325.

Wilcoxon, F. (1945). Individual comparisons

by ranking methods. Biometrics Bulletin,

1(6):80–83.

REFERENCES

Aizawa, A. N. and Wah, B. W. (1994). Scheduling of ge-

netic algorithms in a noisy environment. Evolutionary

Computation, 2(2):97–122.

Castillo, P. A., Gonz

alez, J., Merelo-Guerv

os, J.-J., Prieto,

A., Rivas, V., and Romero, G. (1999). G-Prop-III:

Global optimization of multilayer perceptrons using

an evolutionary algorithm. In GECCO-99: Proceed-

ings Of The Genetic And Evolutionary Computation

Conference, page 942.

Cauwet, M.-L., Liu, J., Teytaud, O., et al. (2014). Al-

gorithm portfolios for noisy optimization: Compare

solvers early. In Learning and Intelligent Optimiza-

tion Conference.

Costa, A., Vargas, P., and Tin

os, R. (2013). Using explicit

averaging ﬁtness for studying the behaviour of rats in

a maze. In Advances in Artiﬁcial Life, ECAL, vol-

ume 12, pages 940–946.

Deb, K. and Goldberg, D. E. (1992). Analyzing deception

in trap functions. In FOGA, volume 2, pages 98–108.

Garc

ıa-Ortega, R. H., Garc

ıa-S

anchez, P., and Merelo,

J. J. (2014). Emerging archetypes in massive

artiﬁcial societies for literary purposes using ge-

netic algorithms. ArXiv e-prints. Available at

http://adsabs.harvard.edu/abs/2014arXiv1403.3084G.

Goldberg, D. E., Deb, K., and Horn, J. (1992). Massive

multimodality, deception, and genetic algorithms. In

R. M

anner and Manderick, B., editors, Parallel Prob-

lem Solving from Nature, 2, pages 37–48, Amsterdam.

Elsevier Science Publishers, B. V.

Jin, Y. and Branke, J. (2005). Evolutionary optimization

in uncertain environments - a survey. IEEE Trans-

actions on Evolutionary Computation, 9(3):303–317.

cited By (since 1996)576.

Jun-hua, L. and Ming, L. (2013). An analysis on con-

vergence and convergence rate estimate of elitist ge-

netic algorithms in noisy environments. Optik - In-

ternational Journal for Light and Electron Optics,

124(24):6780 – 6785.

Liu, J., Saint-Pierre, D. L., Teytaud, O., et al. (2014). A

mathematically derived number of resamplings for

noisy optimization. In Genetic and Evolutionary

Computation Conference (GECCO 2014).

Merelo-Guerv

os, J.-J., Prieto, A., and Mor

an, F.

(2001). Optimization of classiﬁers using ge-

netic algorithms, chapter 4, pages 91–108. MIT

press. ISBN: 0262162016; draft available from

http://geneura.ugr.es/pub/papers/g-lvq-book.ps.gz.

Merelo-Guervs;, J.-J. (2014). Using a Wilcoxon-test

based partial order for selection in evolutionary

algorithms with noisy ﬁtness. Technical report,

GeNeura group, university of Granada. Available at

http://dx.doi.org/10.6084/m9.ﬁgshare.974598.

Merelo-Guervs, J.-J., Castillo, P.-A., and Alba, E. (2010).

Algorithm::Evolutionary, a ﬂexible Perl mod-

ule for evolutionary computation. Soft Computing,

14(10):1091–1109. Accesible at http://sl.ugr.es/000K.

Miller, B. L. and Goldberg, D. E. (1996). Genetic algo-

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

rithms, selection schemes, and the varying effects of

noise. Evolutionary Computation, 4(2):113–131.

Mora, A. M., Fern

andez-Ares, A., Guerv

os, J. J. M.,

Garc

ıa-S

anchez, P., and Fernandes, C. M. (2012). Ef-

fect of noisy ﬁtness in real-time strategy games player

behaviour optimisation using evolutionary algorithms.

J. Comput. Sci. Technol., 27(5):1007–1023.

Mora, A. M., Montoya, R., Merelo, J. J., Snchez, P. G.,

Castillo, P. A., Laredo, J. L. J., Martnez, A. I., and

Espacia, A. (2010). Evolving bot

s ai in unreal. In

di Chio et al., C., editor, Applications of Evolutionary

Computing, Part I, volume 6024 of Lecture Notes in

Computer Science, pages 170–179, Istanbul, Turkey.

Springer-Verlag.

Qian, C., Yu, Y., and Zhou, Z.-H. (2013). Analyzing evo-

lutionary optimization in noisy environments. CoRR,

abs/1311.4987.

Rada-Vilela, J., Johnston, M., and Zhang, M. (2014). Popu-

lation statistics for particle swarm optimization: Re-

sampling methods in noisy optimization problems.

Swarm and Evolutionary Computation, 0(0):–. In

press.

Rudolph, G. (2001). A partial order approach to noisy ﬁt-

ness functions. In Proceedings of the IEEE Confer-

ence on Evolutionary Computation, ICEC, volume 1,

pages 318–325.

Wilcoxon, F. (1945). Individual comparisons by ranking

methods. Biometrics Bulletin, 1(6):80–83.

StudyingandTacklingNoisyFitnessinEvolutionaryDesignofGameCharacters