Evaluating Relevant Opinions within a Large Group

Ana Tapia-Rosero

1,2

and Guy De Tr´e

FIEC, Escuela Superior Polit´ecnica del Litoral, Campus Gustavo Galindo V., Guayaquil, Ecuador

Department of Telecommunications and Information Processing, Ghent University,

St-Pietersnieuwstraat 41, B-9000 Ghent, Belgium

Keywords:

LSP, Evaluation, Relevant Opinions, Shape-similarity Method, Large-scale Group Decision-making.

Abstract:

We propose to identify which opinions are relevant, from the decision-maker’s point of view, within a large

group of opinions that could be collected using social media. Our approach considers that each participating

person expresses his/her preferences over a criterion speciﬁcation as a matter of degree. First, using a shape-

similarity method, we split a large group of opinions, where each opinion is represented through a membership

function, into clusters —here, a cluster depicts a group of similar opinions over the criterion. Then, in order to

evaluate the relevance of each cluster, we differentiate them based on some characteristics like the cohesion,

the number of membership functions and the number of noticeable opinions. Within this paper, the cohesion

of the cluster is a measure that takes into account the level of togetherness among its contained membership

functions; and the representativeness of the cluster is obtained by combining the number of membership

functions and the number of noticeable represented opinions (i.e., considered as more important or worthy of

notice among other opinions). Moreover, relevant clusters result in the evaluation of combining their cohesion

measure and their representativeness according to the decision-maker’s point of view. Finally, as a part of the

evaluation, this proposal includes the steps describing the process through an illustrative example.

1 INTRODUCTION

Nowadays, the use of social media makes it possible

to involve a large group of people to express their

opinions on criteria, e.g., opinion with respect to a

feature like weight, length, or usefulness of a product.

Thus, opinions from different points of view might

be gathered and used in a decision-making context.

Within this paper, each person that belongs to the

aforementioned large group will be considered as an

expert. But, how do we identify and evaluate relevant

opinions in a large group that includes different points

of view and some opinions are more representative

than others? Here, our aim is to evaluate relevance

through the wisdom of the crowd while avoiding to

be overwhelmed with a huge amount of opinions.

Let us consider that a company wants to know

the “usefulness level” (criterion) of a new feature in

a product (e.g., a pressure sensor for an electric tooth-

brush, an augmented reality for a smart phone, a

pedestrian detection in a car, a heart rate monitor in a

cellphone, a pedometer in a waistband, among others)

while the product is under design. Here, it is possible

to gather this information using social media (e.g., a

fan page) where opinions are given by different levels

of knowledge (students, non-experts and profession-

als), areas of expertise (engineering, medicine, jour-

nalism, among others) and personal proﬁles (single,

married, parents, etc.). Hence, it is desired to differen-

tiate noticeable opinions considering their importance

from the decision-maker’s point of view (e.g., the

opinion of some speciﬁc professionals might be more

important than the opinion of some regular users).

Using soft computing techniques, each expert will

express his/her preferences with respect to a speciﬁc

criterion (i.e., level of usefulness) through a mem-

bership function. In this way, experts using expres-

sions like “the usefulness level is above 65%”, “it

is below 50%” or “it is around 30%” could repre-

sent what he/she understands to be the level of use-

fulness through membership functions (Eshragh and

Mamdani, 1979; Pedrycz, 2013). Within this paper, it

is not required that each expert has preknowledge on

soft computing techniques to represent his/her prefer-

ences P(x) as a matter of degree, i.e., 0 ≤ P(x) ≤ 1

where 0 denotes a complete disagreement on a crite-

rion and 1 denotes the highest level of agreement, as

long as they provide some values (Dujmovi´c and De

Tr´e, 2011). These values will be used to deﬁne the

attribute criterion in a membership function.

Tapia-Rosero A. and De Tré G..

Evaluating Relevant Opinions within a Large Group .

DOI: 10.5220/0005087000760086

In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 76-86

ISBN: 978-989-758-053-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Once all the membership functions have been

gathered, we are able to group them using a shape-

similarity method (Tapia-Rosero et al., 2014). The

shape-similarity method obtains clusters of similar

opinions, represented by symbolic notations, facili-

tating their further processing. Each cluster allows

us to obtain the closest approximation to represent a

group of expert opinions by means of its upper and

lower bounds. These boundaries allow us to compute

a cohesion measure among the contained membership

functions, where a higher value denotes more togeth-

erness and hence expresses a group of more conﬁdent

opinions. The main advantage of the proposed cohe-

sion measure is that it is possible to obtain a cluster

where some of the contained membership functions

do not overlap but are close enough to be considered

similar (Tapia-Rosero and De Tr´e, 2013). Notwith-

standing, any cluster with a single membership func-

tion will obtain the highest cohesion value. Therefore,

we consider that besides the cohesion measure, addi-

tional attributes describe a relevant cluster. As well

as one bright bulb could light up a room as good as

a higher number of less brighter bulbs; we consider

that the opinion of one expert might highlight among

others. Based on this analogy, the representativeness

of the cluster is obtained by combining the number of

membership functions and the number of noticeable

opinions.

Since any cluster might be categorized as relevant

based on a combination of the aforementioned char-

acteristics, in this paper we use the logic scoring of

preference (LSP) aggregation (Dujmovi´c, 2007; Du-

jmovi´c et al., 2010) to obtain the overall evaluation

value for each cluster. The LSP aggregation is based

on the verbalized approach of the Generalized Con-

junction/Disjunction (GCD) (Dujmovi´c, 2012) and

allows us to easily reﬂect aspects of human decision-

making, i.e. relative importance given by weights and

a combination of andness and orness. The overall

evaluation values are used in the selection of the rel-

evant clusters and it is made by the decision-maker.

Here, it is possible to select one cluster with the best

evaluation, i.e., the highest overall evaluation value,

or to select a group of the top clusters.

The goal of this proposal is to identify and eval-

uate relevant opinions within a large group from the

decision-maker’s point of view. Within this respect,

it is a challenge trying to accurately reﬂect some-

one’s point of view. However, by using soft com-

puting techniques it is possible to provide a method

to model and handle importance among opinions in-

cluding as a novelty the use of LSP aggregation which

reﬂects aspects of human decision-making. In this pa-

per, we studied how a large group of opinions is re-

duced to some of them considered to be relevant by

the decision-maker.

An advantage within the scope of this proposal

is that it handles a large group of opinions gathered

through social media, where the initially given prefer-

ences are not modiﬁed. Furthermore, it evaluates dif-

ferent points of view separately (i.e., previously clus-

tered) unlike it occurs in some consensual processes

and it permits the decision-maker to select the group

of opinions that best suits his/her choice based on

the combination of some cluster proﬁle characteris-

tics (i.e., cohesion, number of membership functions

and number of noticeable opinions).

The remainder of this paper is structured as fol-

lows. Section 2 gives some preliminary concepts for

clustering similar opinions and computing a cohe-

sion measure. Section 3 describes the LSP method

based on the verbalized approach of the generalized

conjunction/disjunction aggregators. Section 4 de-

scribes how to identify and quantify relevant opin-

ions within a large group using an illustrative exam-

ple that demonstrates its applicability in a decision-

making context. Section 5 concludes the paper and

presents some opportunities for future work.

2 PRELIMINARIES

This section deﬁnes preliminary concepts to prop-

erly understand the remaining sections. These in-

clude concepts on fuzzy sets for representing expert

opinions, some deﬁnitions to cluster similarly shaped

membership functions, and how to compute a cohe-

sion measure denoting the level of togetherness for

each of the clusters.

2.1 Representing Expert Opinions

A membership function µ

, from the preference point

of view, represents a set of more or less preferred val-

ues of a decision variable x in a fuzzy set A. Hereby,

(x) represents the intensity of preference or pref-

erence level in favor of value x (Dubois and Prade,

1997).

In this paper, trapezoidal membership functions

are used considering that they are widely known (Klir

and Yuan, 1995) and they could be built with a few

input values through parameters a, b, c, and d (Equa-

tion 1) to represent the expert preferences over crite-

ria (Dubois, 2000). These dividing points between the

segments, denoted by the aforementioned parameters,

hold the relation a ≤ b ≤ c ≤ d among them.

EvaluatingRelevantOpinionswithinaLargeGroup

(x) =











0 , x ≤ a

x−a

b−a

, a < x < b

1 , b ≤ x ≤ c

d−x

d−c

, c < x < d

0 , x ≥ d

(1)

If we return to the introductory example, trape-

zoidal membership functions allow experts to express

the usefulness level using percentages to denote their

preferences (Eshragh and Mamdani, 1979; Pedrycz,

2013). In this way, experts might use expressions

like “the usefulness level is above 65%” (Figure 1a)

hereby b = 65%, “it is below 40%” (Figure 1b)

hereby c = 40% or “it is between 25% and 50%” (Fig-

ure 1c) hereby b = 25% and c = 50%. These are cases

where P(x) = 1 denote the highest level of preference.

Analogously, other expressions given by the experts

will lead us to denote the lowest level of preference

agreement on the criterion where P(x) = 0.

a b

ba d

c d

(a)

(b)

(c)

P(x) P(x) P(x)

100%

100% 100%

Figure 1: Trapezoidal membership functions expressing ex-

pert preferences through percentages.

Triangular membership functions, a particular

case of trapezium, could be treated considering that b

and c have equal values. This particular membership

function could be used by experts through expressions

“around x” where x denotes the highest level of agree-

ment on the criteria, here x = b = c, and the spread

of less preferred values (i.e., between a and d) might

vary among experts.

2.2 Clustering Similar Opinions: A

Shape Based Approach

Considering that we use a shape-similarity method

proposed in (Tapia-Rosero et al., 2014), within this

subsection some deﬁnitions borrowed from (Tapia-

Rosero et al., 2014) are included to make this paper

self-contained. The shape-similarity method assumes

that similar opinions are reﬂected by similarly shaped

membership functions. It uses as inputs several mem-

bership functions, representing the opinion of experts

over a speciﬁc criterion, and builds clusters of similar

opinions (Figure 2).

The shape-similarity method has three phases that

could be summarized as follows:

1. A shape-symbolic notation for each normal-

ized membership function is built, which depicts

a membership function through a sequence of

symbolic-characters (See Deﬁnition 1).

2. A similarity measure in the unit interval among

shape-symbolic notations is obtained, where 0 de-

notes no similarity and 1 denotes full similarity

between them.

3. A clustering step is performed based on the afore-

mentioned similarity measure between notations.

The clustering stops when the highest similarity

is considered too low according to a previously

determined threshold τ, where 0 ≤ τ ≤ 1. The se-

lected threshold τ allows us to adjust the clusters

starting from the highest similarity with the small-

est number of membership functions (i.e., where

each cluster contains a single membership func-

tion) to a lower similarity with the highest num-

ber of membership functions (i.e., one cluster con-

taining all the membership functions).

Let S

category

and r ∈ S

length

; where t rep-

resents the category of the segment and r depicts its

relative length by means of a linguistic term.

In this way, each segment of the membership func-

tion uses a sign {+,−} to represent its slope, a value

{0, 1} to represent its preference level on the criterion

(i.e., the lowest level or the highest level of agreement

respectively) and a letter {L, I, H} to denote a low, in-

termediate or high point (e.g., a peak in a triangular

membership function corresponds to a high point an-

notated as H). The linguistic term set S

length

, depicted

in Figure 3, expresses the relative length of the seg-

ment on the X-axis by means of labels (e.g., the la-

bel ES corresponds to an “extremely short” segment

while label EL corresponds to an “extremely long”

segment).

Figure 4 shows a trapezoidal membership func-

tion with ﬁve segments, each of them represented by

a shape-symboliccharacter. Thus, the shape-symbolic

notation for this ﬁgure could be expressed as:

h0,Si h+,VSi h1,Si h-,ESi h0,ELi

Hereafter we will consider that using differ-

ent thresholds, different clusters containing simi-

larly shaped membership functions were obtained.

Thus, for each threshold τ a set of k clusters C

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

Phase 1

Symbolic Notation

Phase 2

Calculation

of Similarity

Phase 3

Clustering by

Shape-Similarity

b=c

a=b

Input

Output

Processing

a=b

Shape Similarity Method

b=c

b cd

b c

Figure 2: General architecture of the shape-similarity method.

0.17

0.33

0.83

0.67

0.5

Extremely

Short

Very Short Short Medium Long

Extremely

Long

Very Long

ES VS S M L VL EL

Figure 3: Linguistic term-set S

length

represented by trian-

gular membership functions denoting the relative length of

segments on the X-axis.

Positive slope

<0,S> <1,S> <0,EL>

Negative slope

High preference level

Low preference level

<+,VS>

<-,ES>

µ(x)

Figure 4: Segments of a trapezium and their corresponding

shape-symbolic characters.

, . . . ,C

}, where each cluster C

will be repre-

sented through an array of n characteristics or at-

tributes (a

, . . . , a

) is used.

2.3 A Cohesion Measure for Expert

Preferences

When several clusters of membership functions, rep-

resenting similar expert opinions, are present it is pos-

sible to establish a way to compare them for fur-

ther processing. This paper proposes to use a cohe-

sion measure, which computes the level of togeth-

erness among the membership functions contained

in the cluster. We assume that clusters with a high

level of cohesion are more conﬁdent than those with

a lower cohesion level, since they are closer and do

not necessary overlap. On the one hand, we could

think about a cluster that contains one hundred mem-

bership functions representing the same opinion (i.e.,

each of them has the same membership function rep-

resentation) where we graphically expect a group of

membership functions with the highest cohesion (i.e.,

these membership functions will be drawn one over

the other). On the other hand, we could think about

a cluster with the same amount of membership func-

tions where some of them overlap and others are close

enough to be considered similar. The latter scenario

might lead us to graphically identify the boundaries

where all the membership functions are contained,

however this cluster will have a lower cohesion than

the ﬁrst one. In a decision-making context, the ﬁrst

scenario is the “ideal case” that might be considered

unrealistic, while the second scenario could guide us

to think about a group of similar opinions where the

degree of similarity might be given by a cohesion

measure. For example, Figure 5 shows two clusters

with different levels of cohesion.

There are several strategies to compute the level

of togetherness or cohesion among the membership

Cluster 30

Cluster 50

Figure 5: C

denotes a higher cohesion level than C

EvaluatingRelevantOpinionswithinaLargeGroup

functions contained in a cluster that might be consid-

ered. In (Tapia-Rosero and De Tr´e, 2013) two of them

have been proposed, however in this paper we will

only consider the geometrical approach. The geomet-

rical approach takes into account the area contained

between the upper and lower boundaries compared to

the total available area (Figure 6).

<0,S> <1,S> <0,EL>

<+,VS> <-,ES>

µ(x)

Figure 6: Area contained between boundaries (dark gray)

compared to the available area (light gray).

Equation 2 sets a general form to obtain the cohe-

sion measure in cluster C

with threshold τ based on

these area comparisons.

cohesion(C

, τ) = 1−

− A

. (2)

Hereby, A

denotes the area under the upper

bound, A

denotes the area under the lower bound and

corresponds to the total present area. For illustra-

tion purposes, the computed cohesion for clusters (us-

ing Equation 2) C

and C

with τ = 0.95 are 0.9350

and 0.7547 respectively.

3 LOGIC SCORING OF

PREFERENCE METHOD

Within this paper, the logic scoring of preference

(LSP) method is used to evaluate relevant opinions

considering, as mentioned in Section 2.2, that a set

of k clusters C

= {C

, . . . ,C

} were previously ob-

tained. Here, each cluster C

is represented through

an array of n attributes a

i, j

where i is the identiﬁer of

the attribute and j is the identiﬁer of the cluster.

The LSP method consists of a set of in-

put attributes and elementary criteria reﬂecting the

decision-maker’s point of view on these attributes.

The main advantage lies in that it is possible to build a

precise model of logic aggregation of preferences, by

combining the proper aggregationoperators reﬂecting

the user’s needs (Dujmovi´c and Nagashima, 2006). In

order to proceed with the evaluation, the LSP method

has the following steps:

1) Considering the decision-maker’s point of view, it

is necessary to deﬁne his/her evaluation attributes.

Evaluation of

Relevant Opinions

Cohesion (1)

Representativeness (2)

Number of membership functions (2.1)

Number of noticeable opinions (2.2)

Figure 7: Example of a system attribute tree for evaluating

relevant opinions.

Several attributes can be considered, thus the ﬁrst

step allows us to create a system attribute tree. In

this step, different characteristics or attributes for

relevant clusters of opinions are stated and hier-

archically structured. For example, if we want to

evaluate relevant opinions the decision-maker can

use the structure shown in Figure 7.

The leaves of the tree represent the elementary at-

tributes (a

1, j

, . . . , a

n, j

) of cluster C

. These are

not further decomposed, they have been previ-

ously measured and they are ready to be eval-

uated. Notice that an intermediate node (e.g.

Representativeness), depicts that the attribute has

been decomposed in more elementary attributes

(i.e., number of membership functions and num-

ber of noticeable opinions).

For the sake of readability, the elementary at-

tributes of Figure 7 include their identiﬁers in

parenthesis, i.e. the identiﬁers for cohesion, num-

ber of membership functions and number of no-

ticeable opinions are 1, 2.1 and 2.2 respectively.

2) The evaluation of the elementary attributes is

based on their level of satisfaction or preference.

Thus, the second step is to deﬁne the elementary

criteria, through functions G

that determine the

elementary preference score reﬂecting the accept-

able and unacceptable values of attribute i. In this

step, a fuzzy set for each elementary attribute is

used to represent the decision-maker’s preference.

For example, Figure 8 shows a membership func-

tion representing that the decision-maker accepts

clusters with cohesion ≥ 0.5 but he/she prefers

cohesion ≥ 0.6. Furthermore, the decision-maker

considers that lower values, i.e. cohesion < 0.5,

are not acceptable.

Thus, elementary criteria might be expressed us-

ing piecewise linear approximations of functions

0.5 0.60 1

P (x)

Figure 8: Example of the decision-maker’s preference for

elementary attribute “cohesion”.

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

where after deﬁning certain dividing points be-

tween segments (i.e., parameters a, b, c and d), we

could use linear interpolation between them. As

it has been mentioned in (Dujmovi´c et al., 2010)

“this approach yields a good combination of sim-

plicity and accuracy”.

Once all the elementary criteria G have been de-

ﬁned, it is possible to evaluate all the attributes in

each cluster. Thus, e

i, j

= g

i, j

) corresponds to

the evaluation of attribute i in cluster C

. For ex-

ample, given a

1,30

= 0.9350 which corresponds to

the cohesion of cluster C

we obtain e

1,30

= 1 ac-

cording to the decision-maker’s preference (Fig-

ure 8).

3) In order to satisfy all the decision-maker’s

preferences we need to create an aggregation

structure, which establishes the proper aggre-

gation operators based on the generalized con-

junction/disjunction (GCD) principle (Dujmovi´c,

2007) while being consistent with the previously

created system attribute tree.

For example, in order to obtain the representa-

tiveness of cluster C

it is necessary to take into

account its components (i.e., attributes a

2.1, j

and

2.2, j

) and the level of simultaneity or replaceabil-

ity among them. Figure 9 shows the aforemen-

tioned representativeness annotated as e

2, j

. In a

similar way, we will obtain the evaluation of rel-

evant opinions for cluster C

given by e

, where

we need to aggregate its components e

1, j

and e

2, j

The level of simultaneity or replaceability will be

given by the proper selection of the aggregation

operators represented as A in this Figure.

In this paper, the aggregation structure allows us

to obtain the evaluation of relevant opinions e

for

cluster j. However, to create this structure with

the appropriate selection of aggregation operators

it is necessary to introduce the generalized con-

junction/disjunction principle in the next section.

1,j

2,j

2.1,j

2.1

2.2,j

2.2

Figure 9: Example of the aggregation structure for elemen-

tary attributes 1, 2.1 and 2.2 of cluster C

3.1 Generalized

Conjunction/Disjunction

The generalized conjunction disjunction (GCD) oper-

ator is a continuous logic function that integrates con-

junctive and disjunctive properties in a single func-

tion (Dujmovi´c and Larsen, 2007), denoted as y =

♦. . . ♦x

, x

∈ I = [0, 1], i = 1, . . . , n, and y ∈ I.

GCD includes two parameters: the andness and the

orness. The andness, α ∈ I, expresses the conjunction

degree used to denote simultaneity while the orness,

ω ∈ I, expresses the disjunction degree (Dujmovi´c

and Nagashima, 2006) used to denote replaceability.

These parameters are complementary, i.e., α+ ω = 1.

The location of GCD with respect to conjunction and

disjunction is deﬁned in (Dujmovi´c and Nagashima,

2006) as follows:

♦. . . ♦x

= ω(x

∨ ··· ∨ x

) + α(x

∧ ··· ∧ x

)

If α > 0.5 > ω, the expression x

♦. . . ♦x

is called partial conjunction and is denoted by

∆. . . ∆x

. If α < 0.5 < ω, the expression

♦. . . ♦x

is called partial disjunction and is de-

noted by x

∇. . . ∇x

. If α = ω = 0.5, the expression

♦. . . ♦x

is called the neutrality function, which is

implemented as the arithmetic mean and is denoted

by x

⊖ · ·· ⊖ x

Although GCD can be implemented in sev-

eral ways (Dujmovi´c, 2008), within this paper we

will only consider an implementation based on the

weighted power means (WPM) as follows:

♦. . . ♦x

= (W

+ · ·· +W

)

, (3)

hereby W

denotes the weight assigned to the parame-

ter x

and the parameter r can be computed as a func-

tion of andness α using a suitable numerical approxi-

mation (Dujmovi´c, 2007).

Table 1 includes the corresponding orness, and-

ness and exponent r for 17 levels of GCD imple-

mented using WPM as a reference. Notice that sym-

bols D and C correspond to full disjunction (ω = 1),

and full conjunction (α = 1) respectively.

3.2 GCD Verbalized Approach

The GCD verbalized approach presented in (Duj-

movi´c, 2012) facilitates the use of the LSP method.

Within this approach the decision-maker speciﬁes the

overall degree of importance using a multi-level over-

all importance scale (Table 2) for each attribute.

The multi-leveloverall importance scale has L lev-

els from “lowest” to “highest”, denoted S for simul-

taneity and R for replaceability. Thus, the decision-

maker should provide the overall importance and the

selection of simultaneity or replaceability. This infor-

mation will allow us to obtain the appropriate aggre-

gator.

EvaluatingRelevantOpinionswithinaLargeGroup

Table 1: Aggregation operators for 17 levels of GCD imple-

mented by WPM.

Symbol Orness(ω) Andness(α) Exponent r

D 1 0 +∞

D++ 0.9375 0.0625 20.63

D+ 0.8750 0.1250 9.521

D+- 0.8125 0.1875 5.802

DA 0.7500 0.2500 3.929

D-+ 0.6875 0.3125 2.792

D- 0.6250 0.3750 2.018

D– 0.5625 0.4375 1.449

A 0.5 0.5 1

C– 0.4375 0.5625 0.619

C- 0.3750 0.6250 0.261

C-+ 0.3125 0.6875 -0.148

CA 0.2500 0.7500 -0.72

C+- 0.1875 0.8125 -1.655

C+ 0.1250 0.8750 -3.510

C++ 0.0625 0.9375 -9.06

C 0 1 −∞

Table 2: Overall importance scale with L = 16 levels.

Level Overall importance

16 Highest

15 Slightly below highest

14 Very high

13 Slightly above high

12 High

11 Slightly below high

10 Medium-high

9 Slightly above medium

8 Medium

... ...

0 Lowest

In the case of n attributes of overall importance,

, . . . , S

) for simultaneity, the andness α is deﬁned

as the mean normalized overall importance:

α =

+ · ·· + S

)

, S

∈ [0, L] (4)

In a similar way in the case of replaceability

, . . . , R

), the orness ω is deﬁned as:

ω =

+ · ·· + R

)

, R

∈ [0, L] (5)

Within this paper, clusters with a large number of

membership functions are considered to be important,

but a cluster with a single membership function given

by a noticeable expert might also be relevant. In this

case, the representativeness of the cluster indicates re-

placeability among the number of membership func-

tions and the number of noticeable represented opin-

ions. For example, if the decision-maker considers

that the “representativeness” of a cluster is given by

the number of membership functions (R

considered

as very high) and the number of noticeable opinions

considered as high), the computation of the orness

level is as follows:

ω =

+ R

)

14+ 12

2(16)

= 0.8125. (6)

Once the level of andness/orness have been given

by the decision-maker,we need to map these into nor-

malized weights W

+ · ·· + W

= 1. Although it is

possible to use the GCD verbalized approach to com-

pute the weights with ease (Dujmovi´c, 2012), within

this paper we consider that these will be given by the

decision-maker as well. For example, in the case that

the decision-maker considers the representativeness

components equally important, then both weights are

0.5.

The generalized conjunction/disjunction aggrega-

tion adequately reﬂects the reasoning and preferences

of the decision-maker and it is possible to extend it

with ease, i.e. through changes in the model. In this

paper GDC aggregation principle is used to create

the aggregation structure of the LSP method (step 3)

where the attributes have been evaluated and aggre-

gated taking into account the decision-maker’s pref-

erences.

4 EVALUATING RELEVANT

OPINIONS

The aim of this section is to describe the steps that

allows us to distinguish clusters that are relevant to

represent expert opinions in a group decision-making

context, where these have been gathered through so-

cial media. Here, the main contribution is to provide a

method to handle and model the importance of opin-

ions from the decision maker’s point of view, includ-

ing as a novelty the application of LSP reﬂecting as-

pects of human decision-making.

On the assumption that similar opinions have been

clustered by a shape based approach and that cer-

tain attributes of each cluster are available, we ask

the decision-maker for his/her preferences to reﬂect

his/her point of view in the selection of relevant opin-

ions. Thus, the steps to evaluate relevant opinions us-

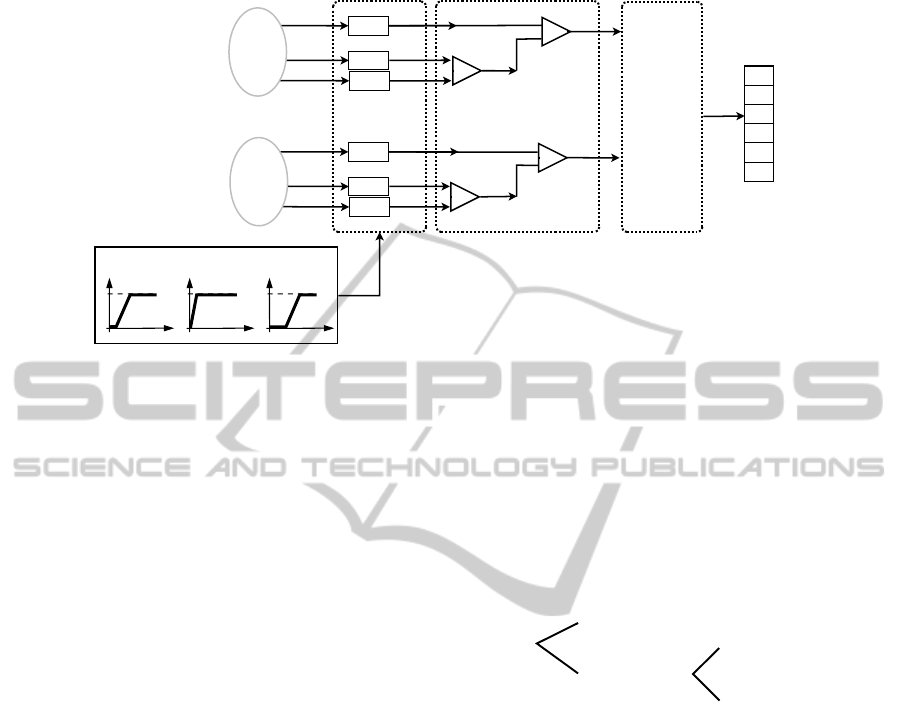
ing LSP are described as follows (Figure 10):

1. Creation of a system attribute tree made by the

decision-maker based on the available attributes

of the cluster. The attributes are hierarchically or-

ganized, where the leaves of the tree correspond to

the elementary attributes selected from the cluster

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

...

1,1

2,1

2.1,1

2.1

2.2,1

2.2

1,k

2,k

2.1,k

2.1

2.2,k

2.2

...

Selection

of Relevant

Clusters

Step 1 Step 2 Step 3 Step 4

Decision-Maker’s Preferences

P (x)

Figure 10: Evaluation of relevant opinions from clusters grouped by shape-similarity.

and the root will lead us to the overall evaluation

value.

2. Deﬁnition of elementary criteria to reﬂect the ac-

ceptable and unacceptable values for each ele-

mentary attribute. These will be given by the

decision-maker as membership functions.

3. Creation of an aggregation structure using the

GCD verbalized approach. This step allows us to

obtain the aggregation operators and weights re-

ﬂecting the decision-maker’s point of view with

ease.

4. Selection of relevant clusters based on the top

overall evaluation values.

For illustration purposes, the aforementioned

steps will be described using the following example.

A company wants to know the perceived“level of use-

fulness” of adding a digital lock (new feature) in a

previously well positioned suitcase model (product),

from a not uniform crowd (i.e., a large group of opin-

ions with different points of view). Therefore, the

company gathered this information using a fan page

of the original product. In this case, the non unifor-

mity of opinions is given by different levels of knowl-

edge, areas of expertise and personal proﬁles. In this

example, the head of the design department acts as the

decision-maker.

The decision-maker considers that all the opin-

ions are important, but those given by a speciﬁc pro-

ﬁle (i.e., frequent ﬂyers) will be considered notice-

able. Additionally, he considers opinions within a

large group relevant.

The opinions about the “level of usefulness”

were clustered by the shape-similarity method pre-

sented in Section 2.2 under the assumption that sim-

ilarly shaped membership functions represent simi-

lar opinions. Hereby, a set of k = 50 clusters C =

, . . . ,C

} have been obtained representing a total

of t = 120 opinions. For each cluster C

the cohesion

measure a

1, j

(cf. Equation 2), the number of mem-

bership functions a

2.1, j

, and the number of noticeable

opinions a

2.2, j

are computed.

Step 1. The decision-maker’s point of view, is re-

ﬂected in the system attribute tree shown in Figure 11.

Evaluation of

Relevant Opinions

Cohesion (1)

Representativeness (2)

Number of membership functions (2.1)

Number of noticeable opinions (2.2)

Figure 11: System attribute tree for evaluating relevant

opinions within a large group.

This system attribute tree establishes that the rep-

resentativeness of the cluster is given by a combina-

tion of the number of membership functions and the

number of noticeable opinions. In a similar way, it

is indicated that the evaluation of relevant opinions is

given by the cohesion and the representativeness of

the cluster.

Step 2. The decision-maker’s preferences were

given through trapezoidal membership functions

(x) for elementary attribute cohesion, P

(x) rep-

resenting the number of membership functions and

(x) for the number of noticeable opinions. These

membership functions are shown in Figure 12.

The aforementioned membership functions reﬂect

his acceptable and unacceptable values for each el-

ementary attribute. As mentioned in Section 3, we

could obtain his preference for values that lie in the

slopes using a linear approximation.

For example, let us consider cluster C

and its at-

EvaluatingRelevantOpinionswithinaLargeGroup

0 0.4 0.6

P (x)

0 4 5

120

P (x)

0 1

120

P (x)

Figure 12: Decision-maker’s preferences for elementary at-

tributes cohesion P

(x), number of membership functions

(x) and number of noticeable opinions P

(x).

Cluster 29

Cohesion: 0.4455 #Membership Functions: 22 #Noticeable Opinions: 0

Figure 13: Cluster C

and its attributes.

tributes a

1,29

= 0.4455, a

2.1,29

= 22 and a

2.2,29

= 0

shown in Figure 13. In order to evaluate the cohe-

sion e

1,29

from the decision-maker’s point of view, we

need to interpolate its value using g

(x) =

x−0.4

0.6−0.4

, as

follows:

1,29

= g

(0.4455) =

0.4455 − 0.4

0.6− 0.4

= 0.2275

Within this step, all the attributes of each clus-

ter will be evaluated using their corresponding func-

tion to reﬂect the decision-maker’s preferences. Thus,

e.g., e

2.1,29

= 1 and e

2.2,29

= 0.

Step 3. In order to build the aggregation struc-

ture it is necessary to select the aggregation opera-

tors properly. In this paper, these will be selected us-

ing the GCD verbalized approach which allows the

decision-maker to use the overall importance scale in

Table 2. In this example, the decision-maker consid-

ers that the cohesion and the representativeness in a

cluster should be simultaneously satisﬁed. Here, the

importance of each attribute has been established as

follows: The cohesion is “high”(S

= 12) and the rep-

resentativeness is “medium high” (S

= 10). With this

approach the level of andness α is given by

α =

12+10

2(16)

= 0.6875

The obtained α value allows us to note that even

though the cohesion and the representativenessshould

be simultaneously satisﬁed, the level of andness is not

too high. Thus the minimal partial conjunction where

both parameters are mandatory is used. In a similar

way the aggregation operator for the representative-

ness is obtained as shown in Equation (6) where the

level of orness ω is 0.8125. These aggregators are

annotated by symbols C − + and D + −, and using

Table 1 we obtained the r exponents -0.148 and 5.802

respectively.

Next, the decision-maker has to select the weight

of each attribute denoting its importance. For in-

stance, if the cohesion is two times more important

than the representativeness then the weights for these

attributes are W

= 0.67 and W

= 0.33 respectively.

In a similar way, if the components for the represen-

tativeness are equally important then their weights are

0.5 (i.e., W

2.1

= W

2.2

= 0.5). Hence, the aggregation

structure to evaluate relevant opinions within a large

group, including the weight of each attribute, is shown

in Figure 14.

0.33

0.67

0.5

2.1

0.5

2.2

D+-

C-+

Figure 14: Aggregation structure based on the decision-

maker’s point of view.

Using the previously obtained aggregation struc-

ture we obtain a single value representing the overall

evaluation of relevant opinions for each cluster (Equa-

tion 3). For illustration purposes, let us compute the

overall evaluation of relevant opinions for cluster C

First, let us evaluate its representativeness given the

selected aggregator D+ −.

2,29

= (0.5(e

2.1,29

)

+ 0.5(e

2.2,29

)

2,29

= (0.5(1)

5.802

+ 0.5(0)

5.802

)

5.802

2,29

= 0.887393

Then, in a similar way, using aggregatorC− + we

will compute the overall evaluation of relevant opin-

ions as follows:

= (0.67(e

1,29

)

+ 0.3(e

2,29

)

= (0.67(0.2275)

−0.148

+ 0.3(0.88739)

−0.148

)

−0.148

= 0.34610

Thus, the evaluation of cluster C

is given by the

previously obtained value.

Notice, that using this approach it is possible

to easily change the input parameters, given by

the decision-maker, in order to accurately represent

his/her point of view. For example, if the decision-

maker would have changed the given weights (i.e.,

33% for cohesion and 67% for representativeness) in

the aggregation structure, the overall evaluation value

would have been 0.5490246.

Step 4. In this step, the purpose of selecting rel-

evant clusters is based on the selection made by the

decision-maker from the previously evaluated clus-

ters. It is possible that some decision-makers select

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications

only the cluster with the best evaluation, i.e. the high-

est value, while other decision-makers prefer to select

a group of the top clusters. Within this example, the

decision-maker had selected the “top 5” clusters rep-

resenting relevant opinions from his point of view.

It is worth to mention that within this example, the

decision-maker started with 120 opinions gathered

from social-media that were grouped into 50 clusters.

Processing these clusters based on this proposal, al-

lowed the decision-maker to select the top 5 clusters

representing relevant opinions taking into account the

cohesion and the representativeness of the clusters.

One of the advantages of the presented approach

is that the ﬂexibility in the LSP method allows the

decision-maker, changing the deﬁnition of elemen-

tary criteria, in order to select relevant opinions that

best suits his/her point of view. One remark within

this respect is that the number of noticeable opin-

ions, considered as a component of the representa-

tiveness, might be extended in order to represent dif-

ferent levels of importance (e.g., low, intermediate,

high, etc.) among experts. In this case, it is possible

to assign different weights to each expert opinion and

its normalization will become part of the criteria def-

inition. In a similar way the number of membership

functions could be replaced by the relative number of

membership functions, considering the total number

of present opinions.

In order to validate the results of this proposal, ﬁve

experts of the soft-computingarea, were asked to rank

a small selection of clusters (i.e., eight clusters from

the original group of 50) based on the cohesion and

the number of membership functions. Here, all the ex-

perts had the same selection for the top 4 and the clus-

ter with the lowest overall evaluation, but the order

of the other intermediate clusters were slightly differ-

ent. Based on the computation described in this pro-

posal, those intermediate clusters had a slightly differ-

ent value in the overall evaluation, which justiﬁes the

small differences among the experts. However, more

elaborated experiments should be performed, and are

subject of further study.

5 CONCLUSIONS

This paper proposed to evaluate relevant opinions

within a large number of expert opinions, expressed

as membership functions, that might be gathered

through social media. A shape-similarity method is

used to cluster similar preferences in order to reduce

the number of evaluations for different points of view.

The evaluation results from selecting the best combi-

nation of cohesion and representativeness in the avail-

able clusters from the decision-maker’s point of view.

The cohesion is a measure obtained from computing

the area among the upper and lower bounds of the

cluster compared to the total available area, while its

representativeness is given by aggregating the num-

ber of membership functions and the number of no-

ticeable opinions. In order to properly reﬂect the

decision-maker’s point of view this proposal uses the

LSP method that buildsa precise representativemodel

of logic aggregation of preferences.

The main advantage of this proposal is that it can

handle a large group of opinions gathered through

social media, where the preferences initially given

are not modiﬁed. Furthermore, it evaluates different

points of view separately (i.e., previously clustered)

and it permits the decision-maker to select the group

of opinions that best suits his/her choice (i.e., given as

preferences in the LSP method) based on the combi-

nation of some cluster proﬁle characteristics. Within

this paper the cluster characteristics or attributes are a

cohesion measure, the relative number of membership

functions and the number of noticeable opinions.

We consider exploring some crowdsourceapplica-

tions as opportunities for future work, and evaluating

clusters of opinions with different strategies in order

to compare them with the presented approach are sub-

ject to further study as well.

ACKNOWLEDGEMENTS

This research is supported by Escuela Superior

Polit´ecnica del Litoral (ESPOL) and it is ﬁnanced by

SENESCYT under Ph.D. studies 2014.

REFERENCES

Cabrerizo, F. J., Ure˜na, R., Pedrycz, W., and Herrera-

Viedma, E. (2014). Building consensus in group deci-

sion making with an allocation of information granu-

larity. Fuzzy Sets and Systems.

Dubois, D. and Prade, H. (1997). The three semantics of

fuzzy sets. Fuzzy Sets and Systems, 90:141–150.

Dubois, D., P. H. (2000). Fundamentals of Fuzzy Sets (THE

HANDBOOKS OF FUZZY SETS Volume 7). Springer.

Dujmovi´c, J. (2007). Continuous Preference Logic for Sys-

tem Evaluation. IEEE Transactions on Fuzzy Systems,

15(6):1082–1099.

Dujmovi´c, J. (2008). Characteristic forms of generalized

conjunction/disjunction. 2008 IEEE International

Conference on Fuzzy Systems (IEEE World Congress

on Computational Intelligence), pages 1075–1080.

EvaluatingRelevantOpinionswithinaLargeGroup

Dujmovi´c, J. (2012). Andness and orness as a mean of over-

all importance. In Fuzzy Systems (FUZZ-IEEE), 2012

IEEE International Conference on, pages 1–6. IEEE.

Dujmovi´c, J. and De Tr´e, G. (2011). Multicriteria meth-

ods and logic aggregation in suitability maps. Inter-

national Journal of Intelligent Systems, 26(10):971–

1001.

Dujmovi´c, J., De Tr´e, G., and Van De Weghe, N. (2010).

LSP suitability maps. Soft Computing, 14(5):421–

434.

Dujmovi´c, J. and Larsen, H. L. (2007). Generalized con-

junction/disjunction. International Journal of Approx-

imate Reasoning, 46(3):423–446.

Dujmovi´c, J. and Nagashima, H. (2006). LSP method and

its use for evaluation of Java IDEs. International Jour-

nal of Approximate Reasoning, 41(1):3–22.

Eshragh, F. t. and Mamdani, E. (1979). A general approach

to linguistic approximation. International Journal of

Man-Machine Studies, 11(4):501–519.

Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic:

Theory and Applications. Prentice Hall.

Pedrycz, W. (2013). Granular Computing: Analysis and

Design of Intelligent Systems. CRC Press.

Tapia-Rosero, A., Bronselaer, A., and De Tr´e, G. (2014). A

method based on shape-similarity for detecting sim-

ilar opinions in group decision-making. Information

Sciences, 258:291–311.

Tapia-Rosero, A. and De Tr´e, G. (2013). A Cohesion

Measure for Expert Preferences in Group Decision-

Making. Systems Research Institute Polish Academy

of Sciences.

FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications