Generation of Numbers with the Distribution Close to Uniform with the

Use of Chaotic Maps

Marcin Lawnik

Faculty of Applied Mathematics, Silesian University of Technology, Gliwice, Poland

Keywords:

Chaos, Pseudo-random Numbers, Uniform Distribution.

Abstract:

The method discussed in the paper enables the generation of values from the distribution close to uniform by

means of “ﬂattening” continuous distributions of (pseudo–) random sequences of numbers. The method makes

use of chaotic maps with uniform distribution. The set of initial conditions for such recursive functions consists

of any sequences of numbers derived in a (pseudo–) random manner. Thanks to an appropriate quantity of

the iterations of such chaotic maps, the initial conditions set is reduced to the sequence of numbers with the

distribution close to uniform. The method may be employed for the derivation of (pseudo–) random values

using for example: sets of physical measurements, values of stock exchange indices or biometrics data like

EEG signals. Consequently, the obtained values may be applied in simulations or in cryptography.

1 INTRODUCTION

Sequences of numbers derived from uniform distribu-

tion are of fundamental importance in many ﬁelds of

science, for example: in cryptography or in simula-

tions.

In cryptography, the sequences derived in a

(pseudo–) random manner give grounds for many ci-

phers, called stream ciphers. Such ciphers use binary

(pseudo–) random sequences for encryption of each

bit of a given message by means of, i.e. XOR func-

tion. When such binary sequences are obtained in

a random manner and additionally other conditions

are fulﬁlled, the ciphering method is proven to be un-

breakable (Stallings, 2011). An easy way to obtain

truly random numbers is through physical measure-

ments, i.e. atmospheric noise (Random.org, 2014)

or chaotic oscillator (Erg

un and

Ozog

uz, 2007), al-

though those generators not always have uniform dis-

tribution (Erg

un and

Ozog

uz, 2007).

In simulations, the sequences of numbers from

the uniform distribution are used, for example, in the

Monte–Carlo method (Metropolis and Ulam, 1949),

which enables the modelling of very complex physi-

cal processes (Binder and Heerman, 2010), ﬁnancial

processes (Boyle, 1977) and others.

The sequences of numbers derived from the uni-

form distribution are also used as basic tools for the

generation of numbers from other types of distribu-

tion, for example – from the normal distribution. Such

sequences may be derived by means of inverse cumu-

lative distribution function (Devroye, 1986) or trans-

formations, for example, the Box–Muller transforma-

tion (Box and Muller, 1958) for the normal distribu-

tion.

To derive pseudo–random numbers from the uni-

form distribution algorithms called Pseudo–Random

Numbers Generators (PRNGs) are used (Blum at al.,

1986; Matsumoto and Nishimura, 1998; Ziff, 1998).

Implementations of such algorithms may be encoun-

tered in any programming language in the form of

ready-made functions (modules) which facilitate easy

generation, for example: rand() in C language or ran-

dom() from the random module in python.

The method presented within the scope of this pa-

per makes it possible to obtain numbers with the uni-

form distribution by means of chaotic maps. The dis-

tribution of the iterative variable of such maps must

be uniform. The set of the initial conditions for such

recursive function consists of any sequences of num-

bers derived in a (pseudo–) random manner, for ex-

ample, stock exchange indices data or biometric data

like EEG signals (Chen, 2014). By means of an ap-

propriate number of iterations the set shall be reduced

to a sequence of numbers with the distribution close

to uniform.

On the other hand an easy method of reducing the

sequence with any distribution to the sequence of uni-

form distribution is the transformation of the output

sequence with the use of its cumulative distribution

451

Lawnik M..

Generation of Numbers with the Distribution Close to Uniform with the Use of Chaotic Maps.

DOI: 10.5220/0005090304510455

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 451-455

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

function. If the sequence of the numbers is derived

from, for example, stock exchange data or EEG sig-

nals, this is impossible.

2 CHAOTIC MAPS WITH

UNIFORM DISTRIBUTION

The most popular chaotic map with uniform distri-

bution widely discussed in scientiﬁc publications is

the so called skew tent map deﬁned by the following

equation:

k+1

(

, x

∈ [0, p)

1−x

1−p

, x

∈ [p, 1]

(1)

where p ∈ (0, 1). For each value of parameter p the

skew tent map is chaotic and the distribution of its it-

erative variable is uniform. For p = 0.5 the recursion

(1) is called tent map.

Another chaotic maps with uniform distribution

are discussed in (Anikin at al., 2008).

The density function ρ(x) of recursive functions

like (1) may be obtained by solving the Frobenius–

Perron equation given by the formula (Ott, 1993):

ρ(x) =

ρ(y)δ[x − M(y)]dy, (2)

where δ(x) is a delta function and M(x) is a recur-

sive function. However, the solution of this equation

is usually impossible. Hence, the following method

is used, as it designates, in a numerical manner, the

distribution of an iterative variable. The whole range

of variable x is divided into N equal sub-ranges. For

each of the sub-ranges, the quantity of the numbers

that fell into it in the course of the iteration of the

recurrence is calculated. The values are successively

denoted as n

, n

, . . . , n

. In the next step the values of

N4x

, . . . ,

N4x

are designated, where 4x denotes

the length of the sub-range. The continuous graph

plotted for the couples of points

i 4 x,

N4x

approx-

imates the density function of the recursive function.

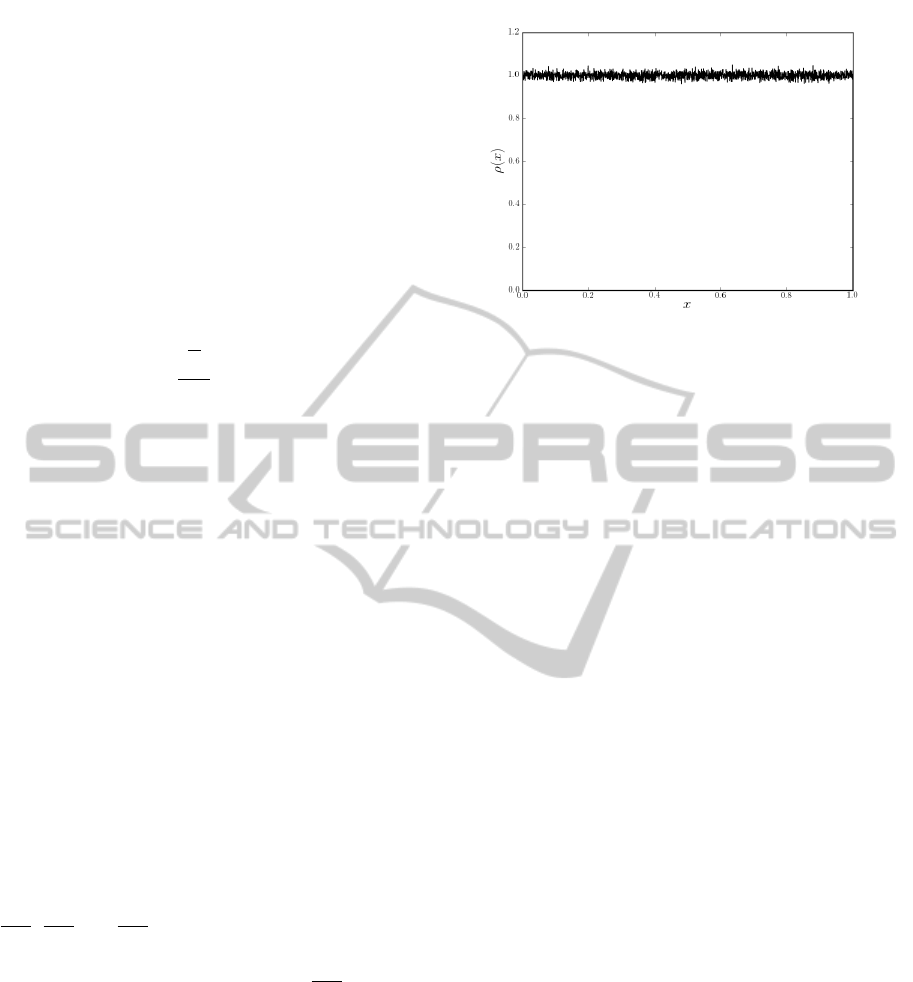
An exemplary distribution numerically derived for

the skew tent map is shown in Figure 1.

The above numerical method was also used to ob-

tain density functions in presented in this paper exam-

ples.

3 THE METHOD

Let T

(x) denote the n-th iteration of the chaotic map

with uniform distribution started at initial condition

Figure 1: The distribution derived numerically for skew tent

map with p = 0.45.

x. Furthermore, let X = {x

, x

, . . . , x

} be a certain

(pseudo–) random sequence with any (even unknown)

distribution. In such case, the sequence of the num-

bers:

U = {u

, u

, . . . , u

} (3)

where u

= T

(

) for i = 0, 1, . . . , M and a is a nor-

malization coefﬁcient, for an appropriate quantity of

iterations n has the distribution close to uniform.

4 EXAMPLES

4.1 Sequence of Pseudo–random

Numbers with Normal Distribution

The sequences of numbers with standard normal dis-

tribution were derived with the use of gauss() func-

tion of module random in language python. By ap-

plying the discussed method with the skew tent map

with p = 0.45 to the sequences, the successive distri-

butions were obtained as shown in Figure 2. Further-

more, as seen in Figure 2, for only n = 4, the distri-

bution of the derived sequence approximates the uni-

form distribution. In Figure 3 dependence (u

, u

k+1

)

between the successive elements of the sequence (3)

was shown in a graphic manner. It may be observed

that the obtained values evenly and without noticeable

dependencies cover the unit square.

4.2 Sequence of Numbers Derived from

the Logistic Map

The logistic map is described by the equation:

k+1

= rx

(1 − x

) (4)

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

452

where r ∈ [0, 4]. For parameter r = 4 the density func-

tion ρ(x) of (4) is equal to (Lasota and Mackey, 1994):

ρ(x) =

x(1 − x)

(5)

The graph in Figure 4 presents the density func-

tion (5) obtained in a numerical manner. By means of

the discussed method, basic distributions shown in the

consecutive graphs in Figure 4 were plotted, whereas,

in Figure 5 dependence (u

, u

k+1

) between the succes-

sive elements of the derived sequence (3) was shown.

For n = 13 the obtained values evenly and without no-

ticeable dependencies cover the unit square.

Figure 2: The derived distributions of the sequence of num-

bers transformed by means of the discussed method with

the skew tent map with p = 0.45 for the successive values

of n = 1, 2, 4. The ﬂattening of the standard normal distri-

bution to the uniform distribution may be observed in the

successive graphs.

Figure 3: Graphic representation of the dependence of the

couples of numbers (u

, u

k+1

) derived from the sequences

in Figure 2.

Figure 4: The derived distributions of the sequence of num-

bers derived from (4) and transformed by means of the dis-

cussed method with the skew tent map with p = 0.45 for the

values of n = 5, 10, 13. The ﬂattening of distribution (5) to

the uniform distribution may be observed.

Figure 5: Graphic representation of the dependence of the

couples of numbers (u

, u

k+1

) derived from the sequences

in Figure 4.

4.3 Japan / U.S. Foreign Exchange Rate

Time Series

Financial time series like stock exchange indices val-

ues are a large data sets, that can be potentially used to

generate pseudo-random numbers. Such time series

have a fractal nature, i.e. while looking at a particular

time series it is impossible to state whether it shows

the relation in the successive years or at a given day

(Mandelbrot and Hudson, 2004). Hence, such type of

numerical data may be used as a set of the initial con-

ditions for the discussed method. As an example the

numerical data from (FRED Economic Data, 2014)

that represents the daily relation between the Japanese

Yen and the USA dollar in the time range starting with

January 4th 1971 are analyzed.

The graph of the time series of the analyzed data

GenerationofNumberswiththeDistributionClosetoUniformwiththeUseofChaoticMaps

453

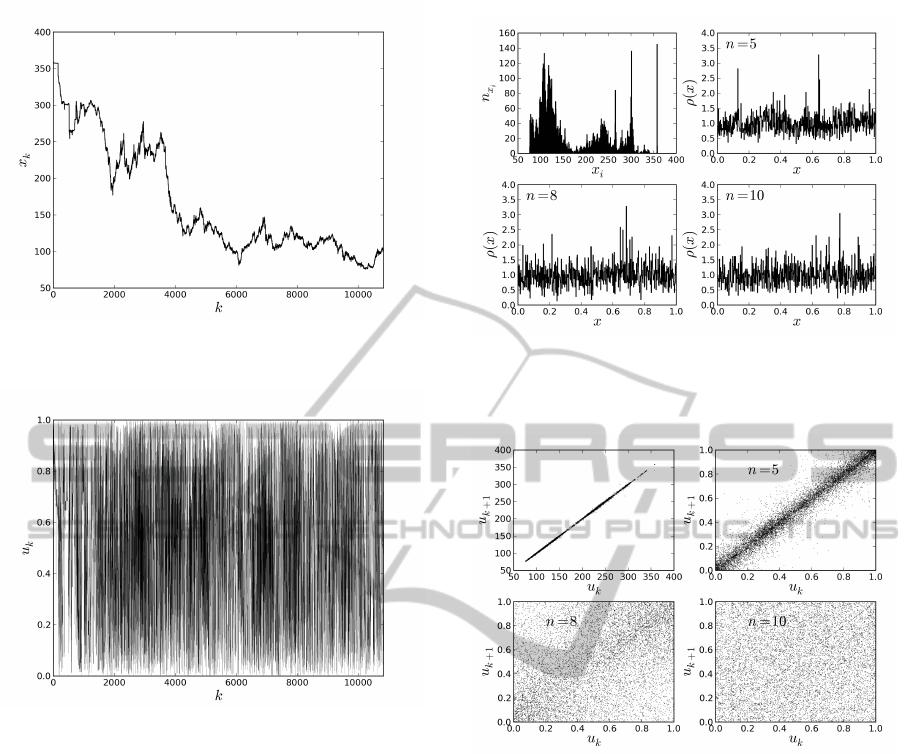
Figure 6: Numerical data describing the relation between

the Japanese Yen and the USA dollar (FRED Economic

Data, 2014).

Figure 7: Time series derived from the sequences in Figure

6 using discussed method with the skew tent map with

p = 0.45 for n = 10.

is presented in Figure 6, whereas, in Figure 7 the ob-

tained time series using the discussed method with the

skew tent map with p = 0.45 for n = 10 is shown.

In Figure 8 the histogram of the data and succes-

sive distributions of the iterative variable derived for

n = 5, 8, 10 are illustrated. As inferred from the graph,

the successive distributions approximate the uniform

distribution. Dependence (u

, u

k+1

) between the suc-

cessive values of the analyzed data is shown in Figure

9. For n = 10 the values cover the unit square evenly

and without noticeable dependencies.

5 CONCLUSIONS

The discussed method enables the generation of num-

bers from the distribution that approximates the uni-

form distribution. The method makes use of chaotic

maps with uniform distribution. The set of the ini-

tial conditions for the recursive functions may be as-

Figure 8: Histogram of the numerical data of the time series

(FRED Economic Data, 2014) and the distributions derived

by means of the discussed method with the skew tent map

with p = 0.45 for n = 5, 8, 10.

Figure 9: Graphic representation of the dependence of the

couples of numbers (u

, u

k+1

) derived from the sequences

in Figure 8.

sumed as any sequence of (pseudo–) random num-

bers. In the course of an appropriate quantity of it-

erations, the set may be reduced to the sequence of

numbers with the distribution approximating the uni-

form one. The method may be applied for generating

(pseudo–) random numbers with the uniform distribu-

tion from a given source, if its distribution is not ﬂat.

Such source may be constituted by, for example, a

set of data derived from physical measurements, val-

ues of stock exchange indices or biometric data like

EEG signals. The sequences generated by means of

the method may be useful for simulations or cryptog-

raphy. Furthermore, the method is very simple for

practical application.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

454

REFERENCES

Anikin, V.M., Arkadaksky, S.S., Kuptsov, S.N., Rem-

izov, A.S., Vasilenko, L.P., 2008. Lyapunov ex-

ponent for chaotic 1D maps with uniform invari-

ant distribution. Bulletin of the Russian Academy

of Sciences: Physics, 72(12):1684–1688.

Binder, K., Heermann, D.W., 2010. Monte Carlo Sim-

ulation in Statistical Physics. An Introduction,

Springer, Berlin 5th edition.

Blum, L., Blum, M., Shub, M., 1986. A Simple Un-

predictable Pseudo-Random Number Generator.

SIAM Journal on Computing, 15(2):364–383.

Boyle, P.P., 1977. Options: A Monte Carlo approach.

Journal of Financial Economics, 4(3):323–338.

Box, G.E.P., Muller, M.E., 1958. A Note on the Gen-

eration of Random Normal Deviates. The Annals

of Mathematical Statistics, 29(2):610–611.

Chen, G., 2014. Are electroencephalogram (EEG)

signals pseudo-random number generators?

Journal of Computational and Applied Mathe-

matics, 268:1–4.

Erg

un, S.,

Ozog

uz, S., 2007. Truly random number

generators based on a non-autonomous chaotic

oscillator. AEU - International Journal of Elec-

tronics and Communications, 61(4):235–242.

FRED Economic Data (2014). Japan / U.S. Foreign

Exchange Rate. http://research.stlouisfed.org

Devroye, L., 1986. Non-Uniform Random Variate

Generation, Springer, New York 1st edition.

Dorfman, J.R., 1999. Cambridge Lecture Notes in

Physics: An introduction to chaos in nonequi-

librium statistical mechanics, volume 14, Cam-

bridge University Press.

Lasota, A., Mackey, M.C., 1994. Chaos, Fractals,

and Noise: Stochastic Aspects of Dynamics,

Springer, New York 2nd edition.

Mandelbrot, B., Hudson, R.L., 2004. The Misbehav-

ior of Markets: A Fractal View of Financial Tur-

bulence, Basic Books.

Matsumoto, M., Nishimura, T., 1998. Mersenne

twister: a 623-dimensionally equidistributed

uniform pseudo-random number generator. ACM

Transactions on Modeling and Computer Simu-

lation, 8(1):3–30.

Metropolis, N., Ulam, S., 1949. The Monte Carlo

Method. Journal of the American Statistical As-

sociation, 44(247):335–341.

Ott, E., 1993. Chaos In Dynamical System, Cam-

bridge University Press.

Truly random numbers (2014).

http://www.random.org/

Stallings W., 2011. Cryptography and Network Secu-

rity: Principles and Practice , Pearson Educa-

tion, 5th edition.

Ziff, R.M., 1998. Four-tap shift-register-sequence

random-number generators. Computers in

Physics, 12(4):385–392.

GenerationofNumberswiththeDistributionClosetoUniformwiththeUseofChaoticMaps

455