
New Solutions for Modeling and Verification of B-based
Reconfigurable Control Systems
Raja Oueslati
1
, Olfa Mosbahi
2
, Mohamed Khalgui
2
and Samir Ben Ahmed
1
1
Faculty of Sciences of Tunis, University of Tunis El Manar, El Manar, Tunisia
2
National Institute of Applied Sciences and Technology , University of Carthage, Carthage, Tunisia
Keywords:
Control System, B method, Reconfiguration, Modeling, Formal Verification, Optimization.
Abstract:
The paper deals with the modeling and verification of B method-based reconfigurable control systems. Recon-
figuration means the dynamic changes of the system behavior at run-time according to well-defined conditions
to adapt it to its environment. A reconfiguration scenario is applied as a response to improve the system
′
s per-
formance, or also to recover and prevent hardware/software errors, or also to adapt its behavior to new require-
ments according to the environment evolution. A new extension called Reconfigurable B “R-B”is proposed to
specify reconfigurable control systems. It consists of two modules: Behavior and Control. The first defines
all possible behaviors of the system, and whereas the second is a set of reconfiguration functions applied to
change the system from a behavioral configuration to another one at run-time. We verify a reconfigurable
control system by using the B method. The goal is to guarantee the consistency and the correctness of the
abstract specification level. The second contribution of this paper deals with the verification of the reconfig-
urable system by avoiding redundant checking of different behaviors sharing similar operations. In order to
control the complexity of verification, an optimal algorithm is developed and a prototyped tool called “Check
R-B”is implemented. The paper
′
s contribution is applied to a benchmark production system FESTO.
1 INTRODUCTION
Control Systems (CS) are special-purpose computer
systems designed to perform one or few dedicated
functions, often with real-time computing constraints
in order to control a physical process in the real world.
Such systems are present in modern life sectors such
as automotive, avionics and industrial automation.
The requirements in industrial CS are increasingly
growing in term of flexibility and agility (Pratl et al.,
2007), (Theiss et al., 2009). In this context, one of
the most important challenges is the trade-offbetween
performance and rapid response to market changes
and customer needs. One of the most promising di-
rections to address these issues is the reconfiguration
of Control Systems (RCS). This functionality refers
to the process of modifying the systems structure and
behavior during its execution. RCS is designed to
take into account the cause triggering reconfigura-
tion, seek quickly and cost-effectively the new config-
uration, implement the reconfiguration without being
taken off-line. Being reconfigurable is important for
reacting fast to sudden and unpredictable requirement
changes with minimum cost and risk.
We are interested in this research in dynamic re-
configurable control systems based on B method. We
have chosen to use the B method (Abrial, 1996) since
it supports code generation from specifications and
it has been used in major safety critical systems in
Europe (Paris Metro Line 14) (Behem et al., 1999)
(Pouzancare, 2003) and is attracting increase interests
in industry. It has a robust and useful tool to sup-
port the specification, design, proof, and code gen-
eration. In particular, a useful tool is developed in
the form of Rodin platform. Currently, industrial ap-
plications involve various areas, such as smart cards
(Casset, 2002), automotive diagnostics (Pouzancare,
2003), (Pouzancare and Pitzalis, 2003) and electronic
circuits (Hallerstade, 2003). Until now, the B method
is used to model static systems in several academic
and industrial research works. Our contribution is
original since we apply B method for the modeling
of RCS.
In this paper, we propose a new formalism called
Reconfigurable B method (R-B) for modeling RCS.
A R-B system is composed of a behavior module and
a control module, where the former is responsible
for the representation of the system behavior accord-
749
Oueslati R., Mosbahi O., Khalgui M. and Ben Ahmed S..
New Solutions for Modeling and Verification of B-based Reconfigurable Control Systems.
DOI: 10.5220/0005091207490757
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 749-757
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ing to reconfiguration levels (architectural, composi-
tional, data) and the latter for the control of reconfig-
uration requests. The behavior module is the union of
all possible behaviors representing the static config-
urations of the system modeled by B machines. The
control module is composed of several reconfigura-
tion functions for switching dynamically the system
from one configuration to another by adding or re-
moving some operations in B machines after recon-
figuration requests (failure or a user request).
Verification of dynamic reconfigurable B control
systems runs up against a combinatorial explosion
problem: the redundant calculation of different be-
haviors sharing similar B machines operations. In
this paper, we propose a suitable optimal algorithm
for controlling as much as possible any combinatory
explosion. After a reconfiguration scenario, we do not
have to verify all operations in a configuration. In ad-
dition, we develop a software tool in order to visually
show for users the checked and unchecked operations
from one configuration to another.
The RCS is a topic that has mobilized a large com-
munity of researchers for manyyears; see for instance
(Khalgui et al., 2011), (Zhang et al., 2013), (Madlener
et al., 2010). The current paper presents a new for-
malism for the modeling and verification of dynamic
reconfiguration systems using B method. It presents
also an algorithm to reduce the required computa-
tions for the verification. Previously, B method has
been employed for the development of static systems.
To our knowledge, this is the first contribution deal-
ing with the B method to dynamically and automati-
cally reconfigure industrial control systems. No one
in related works addresses the same goal of this paper
which is original.
The rest of the paper is organized as follows: in
the second section, we present the background in
which we introduce B method. In the third sec-
tion, We describe the benchmark production System
FESTO to be followed in the paper as a running ex-
ample to explain our contribution. We define, in the
next section, the new Reconfigurable R-B formalism
that we apply to our system. In the fifth section, we
present the optimal algorithm for R-B Control sys-
tems. We finish by a conclusion and the exposition of
our future works.
2 BACKGROUND KNOWLEDGE
We present in this section, the well-known B method.
2.1 Presentation of B
B is a formal method developed by Abrial (Abrial,
1996) to support the software development life cycle
from specification to implementation. It is based on
Zermelo-Fraenkel set theory and on generalized sub-
stitution. Sets are used for data modeling, General-
ized Substitutions (Abrial, 1996) are used to describe
state modification, and the refinement calculus is used
to relate models at varying abstraction levels. A ma-
chine B is composed of three parts:
MACHINE <name>
CONSTRAINTS <constraints>
SETS <sets>
CONSTANTS <constants>
PROPRIETIES <proprieties>
VARIABLES <variables>
INVARIANT <invariant>
INITIALISATION <initialisation>
OPERATIONS <operations>
Dynamic part
Static part
Header part
END
Figure 1: Abstract B machine structure.
• Header part. Allows the identification of the
abstract machine, and contains the clause MA-
CHINE, describing the hostname optionally fol-
lowed by parameters, and the CONSTRAINTS
clause which gives the parameter properties.
• Static part. Includes statements of sets (SETS
clause), constants (CONSTANTS clause) and
variables (VARIABLES clause). These state-
ments are supplemented by a set of predi-
cates describing properties constants (PROPER-
TIES clause) and invariants (INVARIANT clause)
which explain precisely the properties that must
always be satisfied by the state of the machine.
The data defined in these clauses are specified by
using formulas of first order logic and mathemat-
ical notations of set theory.
• Dynamic part. It describes the evolution of the
state machine. This includes initialization of vari-
ables (INITIALISATION clause) and operations
(OPERATIONS clause) that describe the trans-
formations of states corresponding to changes in
the values of variables. Operations are modeled
with Generalised Substitution Language which is
a concept specific to B.
2.2 Composition in B
Abstract machines can be combined, through the
primitives INCLUDES, SEES, IMPORTS and USES
to build new specifications (Abrial, 1996). We are in-
terested to the primitive INCLUDES which allows a
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
750

machine to be included in another one with read/write
access to the variables of the included machine. A
machine M includes a machine M1 means that M has
full access to the constants, sets, variables and oper-
ations of M1 and operations of M can be defined by
using any M1 operations.
Machine M(x,n)
............................
INCLUDES
x.M1, y.M1
OPERATIONS
C= PRE condition THEN x.A|| y.B END
END
Machine M1
............................
............................
............................
OPERATIONS
A= PRE ................THEN .........END
B= PRE ................THEN .........END
END
Figure 2: INCLUDES primitive.
It is worth mentioning that at most one operation of
the included machine can be called from within an
operation of the including machine. In order to avoid
an obvious clash, we have the possibility to rename a
machine while including it. This is done simply by
prefixing, in the INCLUDES clause, the name of the
machine we want to rename with a certain identifier
by a dot (x.M1, y.M1) as explained in Figure 2.
2.3 Proof Obligations
A proof obligation is a mathematical formula to be
demonstrated to ensure that a B model is correct. It
guarantees that initialization should verify the invari-
ant and that each operation should preserve the in-
variant. We are interested in the proof of obligations
relating to an abstract machine that covers the correct-
ness of instance assignments, of initialization and of
operations (Abrial, 1996).
3 CASE STUDY
In order to explain our contribution, we present in the
following section our demonstrator benchmark pro-
duction system FESTO available at Martin Luther
University in Germany. It is served for research and
education purposes in many universities. We define
also operating system constraints that we have taken
into account to achievethe reconfigurationformalism.
3.1 FESTO System
It consists of three units: the distribution unit, the
test unit, the processing unit. The distribution unit is
formed of a pneumatic feeder and a converter which
transmits cylindrical workpieces from a stock to the
test unit. The test unit is composed of a detector, a
tester and an elevator. It performes tests on work-
pieces for height, type of material and color. Work-
pieces that satisfy these tests are transmitted to the
processing unit which is composed of a rotating disk,
a drill machine and a machine control. The rotating
disk is composed of locations to contain and transport
workpieces from the input position, to the drilling po-
sition, to the control position and finally to the output
position.
3.2 Operating System Constraints
In the scope of this paper, we assume that the pro-
cessing unit can operate with two drilling machines
(Drill1 and Drill2) and every machine can use a drill
bit (Drill
bit1 for Drill1 and Drill Bit2 for Drill2) to
perform a hole in the workpieces. The operation of
the system FESTO depends on the number of work-
pieces (NP), the number of workpieces to be drilled
(NP
Init), the drill hole depth, the number of hours
made by the drilling machine (NH
Dm1 Db1 and
NH Dm2 Db2) and the drill bit lifetime (LT Db1 and
LT
Db2). Four production modes can be performed
by FESTO, depending on the number of workpieces,
as follows:
• Light1: If NP < C1 then only Drill1 is used for
drilling workpieces.
• Light2: If NP < C1 then only Drill2 is used for
drilling workpieces.
• Medium: If C1 ≤ NP < C2 then Drill1 or Drill2
are used for drilling workpieces.
• High: If NP ≥ C2 then the two drilling machines
are used simultaneously to drill two pieces at the
same time.
If both Drill1 and Drill2 are broken, the system is
completely stopped. We should make FESTO able
to switch production modes automatically at run-time
according to any changes in the working environment
caused by errors (i.e., Drill1 error or Drill2 error) or
user requirements without a halt. It is assumed that
the production modes are interchangeable as shown
in Figure 3.
Light1
Light2
Medium
High
Drill1 error
or
user
Drill2 error
or
user
user
Drill1 error
Drill2 error
or
user
Drill1 error
or
user
user
user
user
Figure 3: Allowed reconfigurations of FESTO.
NewSolutionsforModelingandVerificationofB-basedReconfigurableControlSystems
751

4 RECONFIGURABLE B
SYSTEMS: R-B FORMALISM
The agent technology is a suitable approach for the
implementation of RCS, further effort still to be done
in order to enhance the applicability of existing ap-
proaches in the industrial domain. The related works
present some limitations, indeed, they support ex-
clusively one of the reconfiguration policies (static,
dynamic, automatic or manual) while a good solu-
tion should support all reconfiguration forms in order
to offer more flexibility and to cover more than one
request of reconfiguration (i.e. to resolve hardware
faults, to add new functionalities, to improve perfor-
mances and to adapt to the environment changes).
Within the proposed approach the reconfiguration
agent is an interactive one which has the ability to
execute different kinds of reconfigurations or to in-
teract with the user in order to enforce a specific ex-
ecution mode in particular situations. Therefore, we
assume that the reconfiguration agent is multi-event
(i.e. can receive more than one reconfiguration re-
quest at once). It monitors the system evolution by
using events notifications and reacts to reconfigura-
tion requests according to their priority values.
In this section, we define reconfiguration levels and
introduce the proposed new formalism R-B to model
RCS with B Method in order to apply it to the FESTO
case study.
4.1 Reconfiguration Levels
In the literature, various levels of dynamic reconfigu-
ration are applied depending on required reconfigura-
tions. The authors in (De Palma et al., 1998) propose
four levels, as follows: modifying the architecture of
an application, modifying the geographical distribu-
tion of an application, modifying the implementation
and interfaces of agents. In (Khalgui and Gharbi,
2010), the authors identify three levels which are ar-
chitectural unit, control unit and data unit. Through-
out our study, we concentrate on three hierarchical re-
configuration levels that we present in the following:
• Architectural reconfiguration (level 1): defines
the different modifications of the system
′
s archi-
tecture when particular conditions are met. This
is done by adding new operations or removing ex-
isting operations,
• Compositional reconfiguration (level 2):
changes the composition of operations for a given
architecture,
• Data reconfiguration (Level 3): changes the val-
ues of variables without changing the system op-
erations.
4.2 Presentation of R-B Formalism
In this section, we propose a new R-B formalism
to model reconfigurable systems following the B
method. A R-B system consists of a behavior mod-
ule which is the union of all system configurations
and a control module formed by a set of reconfigura-
tion functions handling automatic transformations be-
tween specific configurations in the behavior module.
For a R-B system, finite behavior modes (configura-
tions) can be performed and the time cost for the re-
configuration of the control system should be as short
as possible to guarantee the instantaneity, the validity,
and more importantly the safety. Each configuration
model is called a B machine in this paper.
Definition 1. A R-B formalism is a structure defined
as follows :
R-B = (β, R)
Where: β is a behavior module and R is a control
module. The control module is a set of reconfigu-
ration functions R = {r
i
,..., r
m
} allowing automatic
transformations between configurations after receiv-
ing reconfiguration requests to adapt the system to
environment changes, and the behavior module is the
union of n finite behaviors (configurations) of the
system, represented as follows:
β = {M
0
, M
1
, ..., M
i
, ...M
n
}
Where: (i) M
0
is the initial B machine corresponding
to the first configuration, (ii) M
i
is the M
i
machine
represented by the following tuple :
M
i
= (C, S, Const, P, V, I, Init, Op)
Where: (i) C are the system constraints, (ii) S are the
sets, (iii) Const are the constants, (iv) P are the prop-
erties constants , (v) V are the variables, (vi) I are the
invariants, (vii) Init are the initialization of variables
and (viii) Op are the operations.
Definition 2. A reconfiguration function is a structure
r = (Cond, S), where : (i) Cond∈{True, False}: the
pre-condition of r, (ii) S:(
•
M) → (M
•
) is the structure
modification instruction where (
•
M) denotes the ma-
chine M
i
before the application of r and (M
•
) denotes
the target machine M
j
after the reconfiguration func-
tion r is applied. The structure S models the transfor-
mation from a M
i
to another M
j
machine, when we
apply a reconfiguration scenario.
If Cond = True, r is executable, otherwise it cannot
be executed. The structure modification instruction S
guides the system transformation from (
•
M) to (M
•
),
including the addition /removal of operations from a
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
752

source M
i
, to obtain a target M
j
machine.
The pre-condition of a reconfiguration function
means specific external instructions and gusty func-
tioning failures.
Example 1. Let M1 and M2 be as follows:
M1=op
i
; op
j
; op
k
; op
l
; op
m
M2= op
i
; op
j
; op
o
; op
p
; op
n
If Cond
M1,M2
=true. Then the reconfiguration func-
tion r
M1,M2
is executed automatically to respond to
requests. To implement r
M1,M2
, we execute the struc-
ture modification instruction S
M1,M2
, including the re-
moval of the operations op
k
and op
l
and the addition
of op
o
and op
p
. According to the fundamental struc-
ture, the modification of the instructions S
M1,M2
can
be represented as follows:
S
M1,M2
: M1 → M2
4.3 Application to FESTO Case Study
In this section, we apply the proposed formalism to
the FESTO system in order to explain our contribu-
tion. Firstly, we present the operations of all the pos-
sible configurations of the system in order to deter-
mine its behavior module. Secondly, we describe the
FESTO control module. It is composed of a set of re-
configuration functions that make the system able to
switch between specific configurations of the behav-
ior module.
4.3.1 FESTO Operations
We denote by op an operation that transforms the sys-
tem from one state to another. The whole schematic
working process of FESTO with operations is shown
in Figure 4. The set of operations in FESTO is defined
as follows:
• op1: called eject
piece to eject workpieces,
• op2: called convert to transmit workpieces from
Distribution unit to Test unit,
• op3: called Test and performs tests on height and
material type,
• op4: called Tester
failed, it rejects workpieces
which do not satisfy the tests,
• op5: called To
processing unit and transfers the
checked workpieces to the Processing unit,
• op61: called rotate1, it rotates workpieces from
the input position to the drill position,
• op62: called rotate2, it rotates workpieces from
the drill position to the check position,
• op63: called rotate3, it rotates workpieces from
the check position to the output position,
• op7: called Drill1 and drills workpieces by using
Drill1 in the Light1 production mode,
• op8: called Drill2 and drills workpieces by using
Drill2 in the Light2 production mode,
• op9: called Drill and drills workpieces by using
Drill1 or Drill2 in the Medium production mode,
• op10: called Drill1 and Drill2 and drills the work-
pieces by using Drill1 and Drill2 in the High pro-
duction mode,
• op11: called check to check the workpieces after
the drilling step,
• op12: called Remove, it evacuates well drilled
workpieces to another mechanical unit.
Piece
ejection
op1
Convert
op2
Test
op3
Elevate
op5
Rotate1
op61
Drill2
op8
Drill1 or
Drill2
op9
Drill1
and
Drill2
op10
Drill1
op7
Tester
failed
op4
Rotate2 Checker
op11op62
Rotate3
op63
Evacuate
op12
Figure 4: Working process of FESTO.
4.3.2 FESTO Behavior Module
FESTO can perform four types of behavior modes ac-
cording to the production rate. Each behavior mode
can be described by a machine or a combination of
few machines, where a machine is a sequence of or-
dered operations. The FESTO behavior module is
composed of eight machines, as follows:
M1
∆
= op1; op2; op3; op4
M2
∆
=op1; op2; op3; op5; op61; op7; op62; op11;
op63; op12
M3
∆
=op1; op2 ; op3; op5; op61; op7
M4
∆
=op1; op2; op3; op5; op61; op8; op62; op11;
op63; op12
M5
∆
=op1; op2; op3; op5; op61; op9; op62; op11;
op63; op12
M6
∆
=op1; op2; op3; op5; op61; op9
M7
∆
=op1; op2; op3; op5; op61; op10; op62; op11;
op63; op12
M8
∆
=op1; op2; op3; op5; op61; op10
The behavior module β is the union of differ-
ent machines representing the four types of behav-
ioral modes which can be performed by FESTO.
Each mode is specified by a combination of two or
NewSolutionsforModelingandVerificationofB-basedReconfigurableControlSystems
753

three machines. The default initial production mode
Light1, where only Drill1 is used and can be de-
scribed by the combination of M1, M2 and M3. In
fact, after the execution of op3, a workpiece is re-
moved to op4 or op5 according to the result of the test
unit. Similarly, the Light2 production mode is speci-
fied by the combination of M1 and M4, where Drill2
is used. The combinations of M1, M5, M6, and M1,
M7, M8 represent respectively the Medium and High
production modes of the FESTO system. Each con-
figuration of this system is specified by a B machine.
For each B machine, the proof obligations were ver-
ified by the automatic B4free prover and invariants
were preserved by operations.
4.3.3 Control Module of FESTO
In this section, we describe the controller function
allowing automatic changes between all the system
configurations. The controller maintains the correct-
ness of the system, which can be very complex due
to requests of reconfigurations and user requirements.
The switching is done by applying appropriate recon-
figuration functions, according to any environment
change caused by errors or new user requirements.
There are nine different reconfiguration scenarios that
can be applied to FESTO as shown in Figure 3. The
control module of FESTO is represented as follow:
R={ r
Light1,Light2
, r
Light1,Medium
, r
Light1,High
,
r
Medium,Light1
, r
Medium,Light2
, r
Medium,High
, r
High,Light1
, r
High,Light2
, r
High,Medium
}
where each reconfiguration function r has a pre-
condition Cond and a structure modification instruc-
tion S. Let us assume that FESTO is in the Light1
production mode when the user requests to change
the production to Medium. If Cond
Light1,Medium
=true,
then the reconfiguration function r
Light1,Medium
is exe-
cuted automatically to respond to this request. To im-
plement r
Light1,Medium
, we execute the structure mod-
ification instruction S
Light1,Medium
including the re-
moval of the operation op7 and the addition of the op-
eration op9. According to the instruction fundamental
structure modification instructions S
Light1,Medium
is as
follows:
S
Light1,Medium
: M2 → M5
After, S
Light1,Medium
is executed, Drill2 or Drill1 is
used to drill workpieces. FESTO continues to work
in the Medium mode. We define in the following,
an abstract B machine of the controller including M2,
M3, M4, M5, M6, M7 and M8 machines. Therefore,
we use the clause INCLUDES calling the needed ma-
chines. The controller machine is as follows:
MACHINE Controller_machine(........)
CONSTRAINTS
.......................................
INCLUDES
a1.M2(.........),a2.M2(.........), ....
d1.M5(.........),d2.M5(.........),.....
SETS
REQ_USER= {No_Req, L1, L2, M, H};
VARIABLES
req_user
INVARIANT
req_user: REQ_USER
INITIALISATION
req_user:= No_Req
OPERATIONS
M2_to_M5=
SELECT a1.NH_Dm1_Db1<LT_Db1 &
NP_init<C1 & req_user= M
THEN
ANY ...............................
WHERE .............................
THEN
a1.eject_piece (.........)||
a2.convert(.........)||
a3.test_unit (.........) ||
a4.To_processing_unit (....) ||
a5.rotate1(.........) ||
d1.Drill(.........) ||
a7.rotate2(.........) ||
a8.Check (.........) ||
a9.rotate3(.........) ||
a10.Remove(.........)
END
.......................................
where: a1.M2 (resp. d1.M5) represents the instance
of the M2 machine (resp. the instance of M5 ma-
chine). For example, a2.convert (resp. d1.Drill)
means the call of the operation convert (resp. Drill)
from the instance of M2 (resp. M5).
5 VERIFICATION OF R-B
SYSTEMS
Once a R-B system model is well established, the next
step is the optimal verification to avoid redundant cal-
culation. We propose a verification algorithm to solve
the redundancy problem of the operations and to val-
idate B machines. The main idea is to identify for
a given configuration, the operations that should be
checked. An operation should be checked only once
by the B4free prover. So, from a one configuration
to another, only the new operations should be verified
and also old ones that did not respect precedence rela-
tionship between them. We simulate the verification
process by using the developed tool called Check R-B.
The machines (M1, M2, ... , M8) as described in sec-
tion 4 show that some operations are present in all
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
754

Table 1: Operations and presence percentage in B ma-
chines.
Operations Presence percentage
in machines
op1, op2, op3 100%
op4 20%
op5, op6 80%
op11, op12 80%
op7 20%
op8 20%
op9 20%
op10 20%
machines whereas others have a presence percentage
as shown in Table 1.
5.1 Verification Algorithm
In this subsection, we present an efficient optimal al-
gorithm for minimizing the number of verified oper-
ations by the B4free prover. Let ∆ be the set of all
possible operations involved in the different configu-
rations (implementations) of the system. A subset of
tasks included in ∆ is involved in a particular imple-
mentation. We assume in the following that all the
operations of a given configuration are dependents.
∆ = {op1, op2, op3, op4, op5, op61, op62, op63,
op7, op8, op9, op10, op11, op12}
We denote by ∆
Mi
a partition of ∆ containing the op-
erations involved in a particular implementation of a
B machine.
∆
Mi
⊆ ∆
From one machine to another one, we do not have to
check the common operations.
Example 2. Let M1 and M2 be as follows:
M1=op
i
; op
j
; op
l
; op
k
; op
m
M2= op
i
; op
j
; op
l
; op
k
; op
n
If M1 is proven by B4free, and a reconfiguration sce-
nario is applied, the system switches to another re-
configuration M2. For the verification of M2, only the
operation op
n
should be checked because the rest of
operations were already checked in M1.
Example 3. Let M3 and M4 be as follows:
M3 =op
i
; op
j
; op
l
; op
k
; op
m
M4= op
j
; op
i
; op
k
; op
l
; op
n
The verification of M3 can not be used to check M4.
They havethe same fourth operations but not the same
order. Therefore, we must check all the operations of
M4.
Notation. We denote in the following by,
• F: file containing checked machines,
• T: array of checked operations machines,
• k: loop counter of T,
• T[k]: a set of checked operations by B4free,
• Mach: a set of unchecked operations,
• opi: an operation of Mach,
• opj: an operation of T[k],
• Num
checked op: number of checked operations,
• Num
unchecked op: number of unchecked opera-
tions,
• ch1: variable containing the checked operation,
• ch2: variable containing the unchecked operation,
• Max: maximum number of checked operations,
• Checked
operations: checked operations,
• Unchecked
operations: unchecked operations.
The verification process of R-B Control System is de-
scribed as follows:
Algorithm Check R-B
Begin
Read1(F,T);
Read2(Mach);
Verified_op(T,Mach,checked_op,unchecked_op);
Display(checked_op, unchecked_op);
End.
Algorithm Read1
Begin
Read1(F:File;T:Tab);
Open (F)
While (not end F)do
T[k]<-- ligne (F) ;
end
End.
Algorithm Read2
Begin Read2(Mach:string)
Write ("Give the operations to
be checked");
Read(Mach);
End.
Algorithm Verified_op
Begin
Verified_op (T,Mach,checked_op,unchecked_op);
For k=1 to size(T)do
While((i<size(Mach)) and (j<size(T[k])) do
If(opi=opj)
{
ch1=ch1+opi;
Num_checked_op= Num_checked_op+1;
}
Else
{
ch2=ch2+opi;
Num_unchecked_op= Num_unchecked_op+1;
}
end
end
NewSolutionsforModelingandVerificationofB-basedReconfigurableControlSystems
755
If (max< Number_checked_operations)
{
Max= Number_checked_operations;
Checked_operations=ch1;
unchecked_operations=ch2;
}
End.
Algorithm Display
Begin
Write (checked_op, unchecked_op);
End.
Example 1. Behavior module verification
op1
op2
op4
op3
M1
op1
op2
op5
op3
M2
op61
op7
op62
op11
op1
op2
op5
op3
op61
op7
M3
op63
op12
Figure 5: Machines of Light1 production mode.
In the FESTO benchmark production system, the
light production mode Light1 is described by M1,
M2 and M3, as shown in Figure 5. From M1 to M2,
only the fourth operation needs to be checked. From
M2 to M3, no operation needs to be checked again
because they have the same top six operations.
Example 2. Control module verification
op1
op2
op5
op3
M2
op61
op7
op1
op2
op5
op3
op61
op7
M3
op1
op2
op5
op3
M4
op61
op8
op1
op2
op5
op3
M5
op61
op9
op1
op2
op5
op3
M7
op61
op10
Drill1 error
r
Light1,Light2
r
Light1,Light2
r
Light1,Medium
r
Light1,high
op62
op11
op63
op12
op62
op11
op63
op12
op62
op11
op63
op12
op62
op11
op63
op12
Figure 6: Reconfiguration machines of Light1.
As shown in Figure 6, the previous five operations
and the last four operations of M2 and M4 (resp, M5,
M7) are the same. Therefore, the verification process
of M2 can be used in the verification of M4 (resp,
M5, M7). As a result, the same operations have not to
be checked again, only op8 (resp, op9, op10) needs
to be verified. From M2 to M3 no verification process
is required since it is already done for M2.
5.2 Implementation
We develop a Check R-B prototype tool to offer for
users the checked and unchecked operations which
are done by the prover. Then, the tool verifies if these
operations have been already checked by B4free tool.
Concerning the verification of M2, our tool displays
the operations have not been verified by the prover,
since M2 is the first machine introduced to our tool.
Once the operations of the machine M2 are checked
by the prover, they will be saved in the appropriate
file.
Let us assume that the user introduces the machine
M4 (op1; op2; op3; op5; op61; op8; op62; op11;
op63; op12), so a search in a file containing checked
machines will be done. If a sequence of operations
with precedence relationship already exists, it is not
necessary to check it again. Otherwise, it will be for-
warded to the prover.
Figure 7: Simulation of M4.
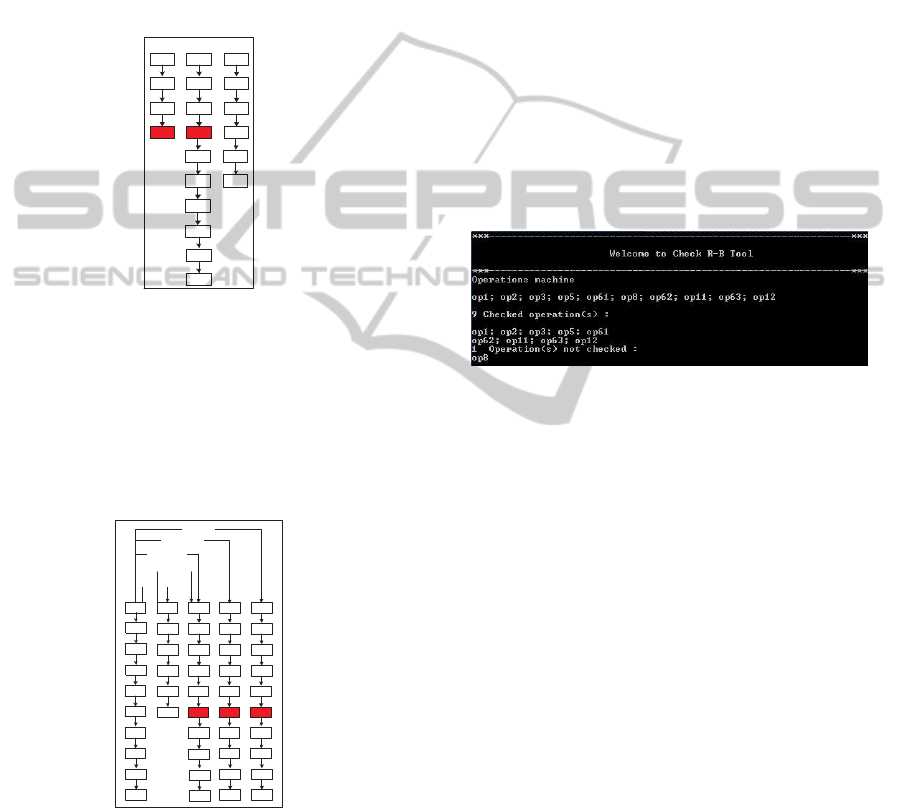
As shown in Figure 7, the sequences of operations
(op1; op2; op3; op5; op61) and (op62; op11; op63;
op12) have already been checked and only the opera-
tion (op8) has to be verified.
In the FESTO benchmark production system, the be-
havior module is composed of eight B machines.
Each production mode is modeled by three B ma-
chines (see section 4). If our system operates in a
default Light1 initial production mode and if Check
R-B tool is used, the number of checked operations
by the proposed verification algorithm is 11. Other-
wise, the number of checked operations without ap-
plying the verification algorithm is 20 (see Figure 5).
In Medium mode (resp, in High mode), and by using
the verification algorithm, the system will check only
one operation (op9) (resp, op10) because the others
operations have been checked for Light1. Without us-
ing the verification algorithm, 20 operations (resp, 20
operations) will be checked.
The FESTO control module makes the system able to
switch from one configuration to another to response
to any change in the environment caused by errors or
new requirements. The execution of each reconfigu-
ration scenario requires the verification of two B ma-
chines (see Figure 6). Let us assume that FESTO is in
the Light1, if the user requests to change the produc-
tion mode, the system switches from Light1 to Light2
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
756
(resp, Meduim, High), the prover checks 20 opera-
tions. When the system is in Light1 and by using the
prototype tool, 11 operations will be verified. Fur-
ther more, if Drill1 breaks down, the system switches
from Light1 to Light2, the prover checks 16 opera-
tions, otherwise 11 operations. These different exper-
imentations clearly show the benefits of the proposed
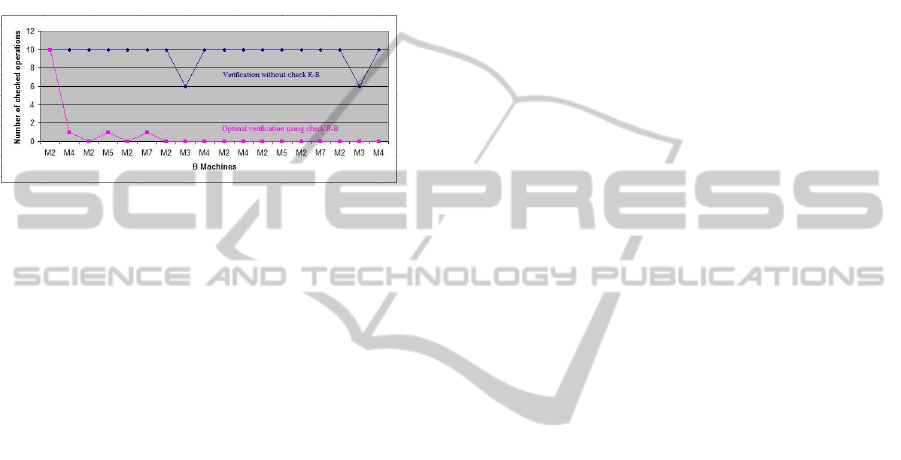
algorithm. Figure 8, presents the advantages of Check
R-B when the system runs (M2, M4, M2, M5, M2,
M7, M2, M3, M4) in order.
Figure 8: Comparison between verification process with
and without using Check R-B .
6 CONCLUSION
In this paper, we have proposed a new Reconfigurable
B formalism to reconfigure control systems following
the B method. This formalism consists of behavior
and a control modules. The first one is modeled by
different abstract machines describing all the possible
behaviors of the system according to three reconfig-
uration levels : architectural, structural and data lev-
els. The second module allows the system to dynam-
ically switch from one configuration to another dur-
ing a power failure or a user request. The proposed
formalism has been applied to the FESTO system.
We have specified all the different configurations with
B method and have verified all the proof obligations
with the powerful tool B4free. We have also proposed
an optimal algorithm to verify reconfigurable B con-
trol systems. It indicates for a given configuration,
which operations have to be verified. An operation
should be only once checked by the prover. Thus,
from a configuration to another one, we verify only
the new operations. We have proved the optimality
and the efficiency of our algorithm with this origi-
nal tool. We report the experimental results, which
demonstrate an improvement of up to 50% as com-
pared to a direct verification.
This paper is a first step, where we focus on mod-
eling and verification of reconfigurable B centralised
system. Several points will be addressed in the future
work. Firstly, we plan to apply the R-B formalism for
distributed systems. Secondly, we plan to develop a
new verification algorithm for these systems.
REFERENCES
Abrial, J.-R. (1996). The B-Book. Cambridge University
Press.
Behem, P., Benoit, P., and Meynadier, J. (1999). Me-
teor: A successful application of b in a large project.
pages 369–387. In FM99-World Conference on for-
mal Methods in the Development of Computing Sys-
tems, Springer - Verlag.
Casset, L. (2002). Development of an embedded verifier
for java card byte code using formal methods. Formal
methodes, 2391:290–309.
De Palma, N., Bellissard, L., and Riveill, M. (1998).
Dynamic reconfiguration of agent-based applica-
tions. pages 369–387. in Proceedings of the Eu-
ropean SIGOPS Workshop: Support for Compos-
ing Distributed Applications, ACM, Sintra, Portugal,
Springer - Verlag.
Hallerstade, S. (2003). Parallel hardware design in b, in
didier bert. pages 101–102. Formal specification and
Development in Z and B, Springer - Verlag.
Khalgui, M. and Gharbi, A. (2010). Development of an
embedded verifier for java card byte code using for-
mal methods. Ubiquitous Systems and Pervasive Net-
works, 1(1):19–28.
Khalgui, M., Mosbahi, O., Li, Z., and Hanisch, H.-M.
(2011). Reconfigurable multiagent embedded con-
trol systems from modeling to implementation. IEEE
Trans. Computers, 60(4):538–551.
Madlener, F., Weingart, J., and Huss, S. (2010). Verifica-
tion of dynamically reconfigurable embedded systems
by model transformation rules. 4th IEEE/ACM Inter-
national conference on Hardwave-Software Code sign
and System Synthesis (CODES+ISSS 2010), part of
the Embedded Systems Week.
Pouzancare, G. (2003). How to diagnose a modern car with
a formal b model. volume 2651, pages 98–100. For-
mal specification and Development in Z and B, In-
ternational Conference of B and Z Users (ZB2003),
Turku, Finland, Springer - Verlag.
Pouzancare, G. and Pitzalis, J. (2003). Modlisation en b
vnementielle des fonctions mcaniques, lectriques et
informatiques dun vhicule. Technique et Science In-
formatiques, 22(1):119–128.
Pratl, G., Dietrich, D., Hancke, G., and Penzhorn, W.
(2007). A new model for autonomous, networked con-
trol systems. IEEE Transactions on Industrial Infor-
matics, 3(1):21–32.
Theiss, S., Vasyutynsky, V., and Kabitzsch, K. (2009). Soft-
ware agents in industry: A customized framework in
theory and praxis. IEEE Transactions on Industrial
Informatics, 5(2):563–577.
Zhang, J., Khalgui, M., Li, Z.and Senior Member, I., and
Mosbahi, O. (2013). R-tnces: A novel formalism for
reconfigurable discrete event control systems. IEEE
Transactions On Systems, Man, And Cybernetics, Part
A: Systems And Humans, 43(4):757 – 772.
NewSolutionsforModelingandVerificationofB-basedReconfigurableControlSystems
757
