A Self-adaptive Iterated Local Search Algorithm on

the Permutation Flow Shop Scheduling Problem

Xingye Dong

, Maciek Nowak

, Ping Chen

and Youfang Lin

Beijing Key Lab of Trafﬁc Data Analysis and Mining, School of Computer and IT,

Beijing Jiaotong University, Beijing 100044, China

Quinlan School of Business, Loyola University, Chicago, IL 60611, U.S.A.

TEDA College, NanKai University, Tianjin 300457, China

Keywords:

Scheduling, Permutation Flow Shop, Total Flow Time, Iterated Local Search, Self-adaptive Perturbation.

Abstract:

Iterated local search (ILS) is a simple, effective and efﬁcient metaheuristic, displaying strong performance on

the permutation ﬂow shop scheduling problem minimizing total ﬂow time. Its perturbation method plays an

important role in practice. However, in ILS, current methodology does not use an evaluation of the search

status to adjust the perturbation strength. In this work, a method is proposed that evaluates the neighborhoods

around the local optimum and adjusts the perturbation strength according to this evaluation using a technique

derived from simulated-annealing. Basically, if the neighboring solutions are considerably worse than the

best solution found so far, indicating that it is hard to escape from the local optimum, then the perturbation

strength is likely to increase. A self-adaptive ILS named SAILS is proposed by incorporating this perturbation

strategy. Experimental results on benchmark instances show that the proposed perturbation strategy is effective

and SAILS performs better than three state of the art algorithms.

1 INTRODUCTION

Since the pioneering work of Johnson (Johnson,

1954), the permutation ﬂow shop problem (PFSP)

has attracted considerable attention. In this problem,

there are n jobs and m machines, and each job has m

operations. The jobs need to be processed on m ma-

chines in the same sequence, that is to say no pre-

emption is allowed. The ith operation of each job

needs to be processed on the ith machine. All the

jobs are available at time zero and each machine can

serve at most one job at any time. Any operation

can be processed only if its previous operation has

been processed and the requested machine is avail-

able. The PFSP is NP-complete when minimizing

total ﬂow time with more than one machine (Garey

et al., 1976).

For the purpose of ﬁnding high-quality solutions

within a reasonable computation time, many methods,

including simple heuristics and more complex meta-

heuristics (Dong et al., 2013), have been proposed.

Among the existing metaheuristics, local search pro-

cedure plays an important role. Several ant colony

algorithms are proposed by Rajendran et al. (Rajen-

dran and Ziegler, 2004; Rajendran and Ziegler, 2005),

working with well designed local search procedures

and performing better than some constructive heuris-

tics by Liu and Reeves (Liu and Reeves, 2001). Tas-

getiren et al. (Tasgetiren et al., 2007) apply a par-

ticle swarm optimization (PSO) algorithm by using

the smallest position value rule. They also propose a

hybrid algorithm with variable neighborhood search

(VNS), called PSO

VNS

, and it performs quite well on

Taillard’s benchmark instances (Taillard, 1993). Pan

et al. (Pan et al., 2008) develop two metaheuristics, a

differential evolution algorithm and an iterated greedy

algorithm hybridized with a referenced local search

procedure. Local search procedures are also used

in several genetic algorithms (Tseng and Lin, 2009;

Zhang et al., 2009; Tseng and Lin, 2010). Recently,

Tasgetiren et al. (Tasgetiren et al., 2011) designed an

artiﬁcial bee colony algorithm and a discrete differen-

tial evolution algorithm. Both algorithms use a local

search procedure taking advantage of the iterated lo-

cal search (ILS) by Dong et al. (Dong et al., 2009) and

the iterated greedy (IG) algorithm by Ruiz and St¨utzle

(Ruiz and St¨utzle, 2007). An asynchronous genetic

local search algorithm, embedding an enhanced vari-

able neighborhood search, is also addressed by Xu et

al. (Xu et al., 2011) for the PFSP minimizing total

378

Dong X., Nowak M., Chen P. and Lin Y..

A Self-adaptive Iterated Local Search Algorithm on the Permutation Flow Shop Scheduling Problem.

DOI: 10.5220/0005092003780384

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 378-384

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ﬂow time.

Local search procedure is used as an embed-

ded procedure in the aforementioned metaheuristics.

However, it is also used in an iterative way to form a

metaheuristic called iterated local search (ILS). Dong

et al. (Dong et al., 2009) develop an ILS to solve the

PFSP minimizing total ﬂow time, in which the per-

turbation method swaps several pairs of adjacent jobs

and the perturbation strength, denoted by the number

of swapping pairs, is evaluated. A multi-restart iter-

ated local search (MRSILS) algorithm is proposed by

Dong et al. (Dong et al., 2013), improving the per-

turbation method mainly by generating restart solu-

tions from a set of elite solutions. Their experiments

show that the MRSILS increases the performance of

the methodology used in Dong et al. (Dong et al.,

2009) signiﬁcantly, while performing comparably to

or better than ﬁve other state of the art metaheuristics

(Pan et al., 2008; Zhang et al., 2009; Tasgetiren et al.,

2011). Costa et al. (Costa et al., 2012b) study the

combination of the most commonly used local search

neighborhoods, the swap neighborhood and the in-

sertion neighborhood. Six different combinations in

total are calibrated. Later, they extend this work

by developing an algorithm hybridizing VNS and

path-relinking on a particle swarm framework, with

promising experimental results on Taillard’s bench-

mark instances (Costa et al., 2012a). Pan and Ruiz

(Pan and Ruiz, 2012) propose two local search meth-

ods based on the well known ILS and IG frameworks.

They also extend them to population-based versions;

however, their experiments show that the two local

search methods perform better than the population-

based versions.

Though ILS has performed well on the PFSP min-

imizing total ﬂow time, one limitation is that the

search process often cannot improve the best solution,

even with dozens of iterations. For example, this oc-

curs with the MRSILS by Dong et al. (Dong et al.,

2013), although the pooling strategy in this algorithm

augments the ability to ﬁnd better solutions. A reason

for the search process to be limited is that the pertur-

bation method moves randomly selected jobs to other

randomly selected positions without considering the

search status. In order to improve perturbation qual-

ity, this work proposes a method to evaluate the con-

vergence status of the search. With a greater focus

on convergence, the probability increases that a job is

moved to a position where a solution with larger ob-

jective can be generated. Based on this observation,

a self-adaptive ILS (SAILS) is proposed and evalu-

ated. Comparison results with the MRSILS by Dong

et al. (Dong et al., 2013) and two local search based

algorithms by Pan and Ruiz (Pan and Ruiz, 2012) on

Taillard’s benchmark instances (Taillard, 1993) show

that the new perturbation method leads to improved

performance.

The remainder of this paper is organized as fol-

lows. In Section 2, the formulation of the PFSP with

total ﬂow time criterion is presented. Section 3 de-

scribes the evaluation method and illustrates the pro-

posed algorithm. The evaluation method is analyzed

and SAILS is compared with several state of the art

algorithms in Section 4, then the paper is concluded

in Section 5.

2 PROBLEM FORMULATION

In this paper, the PFSP is discussed with the objective

of minimizing total ﬂow time. This problem is an im-

portant and well-known combinatorial optimization

problem. In the PFSP, a set of jobs J = {1, 2,.. .,n}

available at time zero must be processed on m ma-

chines, where n ≥ 1 and m ≥ 1. Each job has m oper-

ations, each of which has an uninterrupted processing

time. The processing time of the ith operation of job j

is denoted by p

, where p

≥ 0. The ith operation of

a job is processed on the ith machine. An operation

of a job is processed only if the previous operation

of the job is completed and the requested machine

is available. Each machine processes these jobs in

the same order and at most one operation of each job

can be processed at a time. The PFSP to minimize

total ﬂow time is usually denoted by F

|prmu|

∑

(Pinedo, 2001), where F

describes the environment,

prmu is the set of constraints andC

denotes the com-

pletion time of job j. Let π denote a permutation on

the set J, representing a job processing order. Let

π(k), k = 1,.. .,n, denote the kth job in π, then the

completion time of job π(k) on each machine i can be

computed through a set of recursive equations:

i,π(1)

∑

r=1

r,π(1)

i = 1,.. .,m

(1)

1,π(k)

∑

r=1

1,π(r)

k = 1,. .. ,n

(2)

i,π(k)

= max{C

i−1,π(k)

i,π(k−1)

} + p

i,π(k)

i = 2,.. .,m;k = 2,.. .,n

(3)

Then C

π(k)

= C

m,π(k)

, k = 1,.. ., n. The total ﬂow

time is

∑

π(k)

, or the sum of completion times on ma-

chine m for all jobs. The objective of the PFSP when

minimizing total ﬂow time is to minimize

∑

π(k)

, or

for short.

3 THE PROPOSED ALGORITHM

According to Lourenco et al. (Lourenc¸o et al., 2010),

the general framework of ILS has four key compo-

ASelf-adaptiveIteratedLocalSearchAlgorithmonthePermutationFlowShopSchedulingProblem

379

nents: the method generating the initial solution, the

local search procedure, the acceptance criterion and

the method to perturb a solution. In this work, the

H(2) heuristic by Liu and Reeves (Liu and Reeves,

2001) is used to generate the initial solution, as it can

generate an initial solution in negligible time and has

been used by Dong et al. (Dong et al., 2013; Dong

et al., 2009) to form quite good ILS algorithms. As

for the other three key components, the local search

procedure and the evaluation method used to indicate

the convergence status are discussed in Section 3.1.

The acceptance criterion and the perturbation method

are addressed together in Section 3.2. Finally, the pro-

posed ILS algorithm is illustrated in Section 3.3.

3.1 Evaluation Method and Local

In this work, a solution to the discussed problem is

presented as a permutation of the jobs and the com-

monly used insertion local search is chosen as the lo-

cal search procedure. During the local search, each

job is removed from its original position and inserted

into the other n− 1 positions to see whether the so-

lution can be improved. Suppose the current local

optimum solution is π and f

π(i), j

denotes the objec-

tive value of the solution generated by removing job

π(i) and inserting it into position j. Among the n − 1

solutions, the best one is chosen and its objective is

denoted by f

∗

π(i)

. The objective values form a matrix

F, called the objective matrix. For all of the jobs,

the average objective value of f

∗

π(i)

,i = 1,. ..,n can be

computed as:

avg

∑

i=1

∗

π(i)

. (4)

This average objective value can be used as an in-

dicator of the convergencestatus. Suppose the current

best objective value in the search process is f

. The

larger the difference avg

− f

, the worse the solutions

in the neighborhood surrounding π and the more dif-

ﬁcult it is to escape from the local minimum in this

neighborhood. This is an indicator that the perturba-

tion strength should be increased. In order to tem-

per the inﬂuence of this indicator as the difference be-

tween avg

and f

becomes larger, this difference is

adjusted such that:

avg

′

= (avg

− f

)

1/k

. (5)

where k is an integer, and its value is tuned in Section

The local search used in this work is shown in Fig-

ure 1, where π denotes the start solution, π

∗

denotes

procedure Insertion

LS(π)

1. cnt ← 0, idx ← 0, π

seq

← π

∗

;

2. while (cnt < n) do

3. Find j, where π( j) = π

seq

(idx + 1);

4. Move π( j) to other n− 1 positions in

π, respectively; denote the best solut-

ion as π

′

; update F

concurrently;

5. if C

′

< C

then

6. π ← π

′

, cnt ← 0;

else

7. cnt ← cnt + 1;

endif

8. if C

< C

seq

then

9. π

seq

← π;

endif

10. idx ← (idx+ 1) mod n;

endwhile

11. return π;

end

Figure 1: Pseudo code of the insertion local search.

the best solution found so far in the search process,

and F

∗

denote the objective matrices corre-

sponding to π and π

∗

, respectively.

3.2 Acceptance and Perturbation

Method

In the general framework of the ILS (Lourenc¸o et al.,

2010), a decision is made whether to accept a solution

as the local optimum when it is reached, and then the

solution may be perturbed to generate a restart solu-

tion that continues the local search procedure. Dong

et al. (Dong et al., 2013) propose a pooling strat-

egy that leads the search to a more promising solu-

tion space, generating highly competitive solutions.

In this work, the pooling strategy is also used, while

the perturbation method is adapted by using the indi-

cator avg

′

and incorporating the concept of tempera-

ture control from simulated annealing (Nikolaev and

Jacobson, 2010).

According to Dong et al. (Dong et al., 2013),

a set of elite solutions is pooled during the local

search. Suppose the set of elite solutions is pool

and π is the solution chosen from it. It is perturbed

by randomly selecting a job, i, and moving it to

another randomly selected position with probability

exp(−avg

′

/T), where T denotes temperature. In this

work, T is a constant value. Alternatively, with prob-

ability 1− exp(−avg

′

/T) the randomly selected job

is moved to a position that can generate a worse so-

lution. The probability of moving job i to position j,

where j 6= i, is denoted by p

and can be determined

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

380

procedure Perturbation()

1. if |pool| < pool size then

2. π ← π

∗

, F

← F

∗

;

else

3. Choose a solution from pool as π, get

the corresponding F

from F

pool

;

endif

4. Compute avg

′

using F

;

5. Randomly select a job π(i) from π;

6. if rand() < exp(−avg

′

/T) then

7. Move π(i) to another randomly selected

position in π to form a new π;

else

8. Move π(i) to another position in π acc-

ording to Eq. (6) to form a new π;

endif

9. return π;

end

Figure 2: Pseudo code of the perturbation method.

Table 1: Global variables used in the perturbation method.

variables Description

∗

The best solution found so far

π A variable denotes a solution

pool The set of elite solutions

pool

size The size limitation of pool

Objective matrix corresponding to π

∗

Objective matrix corresponding to π

∗

pool

Pool of objective matrix correspond-

ing to pool

using a roulette methodology, such that the probabil-

ity increases with the cost of the solution generated

by the move. This probability is determined as:

π(i), j

− f

+ 1

∑

k=0;k6=i

π(i),k

− f

+ 1

(6)

The perturbation method is illustrated in Figure 2.

In this ﬁgure, rand() is a function that generates a

random number uniformly distributed in the range [0,

1], and the global variables are listed in Table 1.

3.3 Self-adaptive ILS

The proposed ILS is named self-adaptive ILS

(SAILS), with the pseudo code presented in Figure

In this work, the pool

size is set to 5, as this value

is found to be effective in Dong et al. (Dong et al.,

2013), although the parameter is rather robust. The

parameter k (used in Eq. (5)) and temperature T are

tuned in Section 4.1. There are usually two termi-

nation criteria in the literature: a maximum number

of iterations and limited computational time. In this

1. Define pool

size, k and T;

2. π ← Generate an initial solution;

3. Initialize F

by setting every entry to C

;

4. π

∗

← π; F

∗

← F

; pool ←

0; F

pool

←

5. while(termination criterion is not satisﬁed) do

6. π ← Insertion

LS(π);

7. if C

< C

∗

then

8. pool ←

0, F

pool

←

0, F

∗

← F

;

endif

9. if π /∈ pool then

10. Add π to pool, add F

to F

pool

;

endif

11. if |pool| > pool

size then

12. Delete the worst solution in pool, and the

corresponding objective matrix in F

pool

;

endif

13. π ← Perturbation();

end

14. Output π

∗

and stop.

Figure 3: Pseudo code of the proposed SAILS.

work, the latter is applied on line 5 in order to more

easily compare the SAILS with other algorithms.

In considering insertion local search, the number

of solutions to be evaluated is at least n × (n − 1)

and the time complexity for evaluating one solution

is O(nm), so the time complexity of the local search

is at least O(n

m). In literature, the CPU time limi-

tation is often set to ρnm milliseconds, where ρ is a

constant (Tasgetiren et al., 2007; Ruiz and St¨utzle,

2007; Xu et al., 2011; Costa et al., 2012b; Costa

et al., 2012a; Pan and Ruiz, 2012). This setting has

a shortcoming in that smaller instances can run with

more CPU time relative to larger instances. For ex-

ample, an instance with 20 jobs and 20 machines

may have 1000× 20× (20− 1) solutions evaluated in

ρ× 20× 20 milliseconds CPU time, i.e. checking all

the jobs 1000 passes; while an instance with 500 jobs

and 20 machines still has the same number solutions

evaluated in ρ× 500× 20 milliseconds CPU time, i.e.

checking all the jobs only about 1.52 passes. In or-

der to avoid this unfair, the CPU time limitation is set

to ρn

m milliseconds. In this work, ρ is set to 0.004,

0.012 and 0.02, respectively.

4 COMPUTATIONAL RESULTS

In this section, the proposed algorithms are evaluated.

Firstly, two parameters of the SAILS are tuned, then

the SAILS is compared with state of the art algorithms

and shown the effective of the newly proposed pertur-

bation method.

The benchmark instances used for analysis are

ASelf-adaptiveIteratedLocalSearchAlgorithmonthePermutationFlowShopSchedulingProblem

381

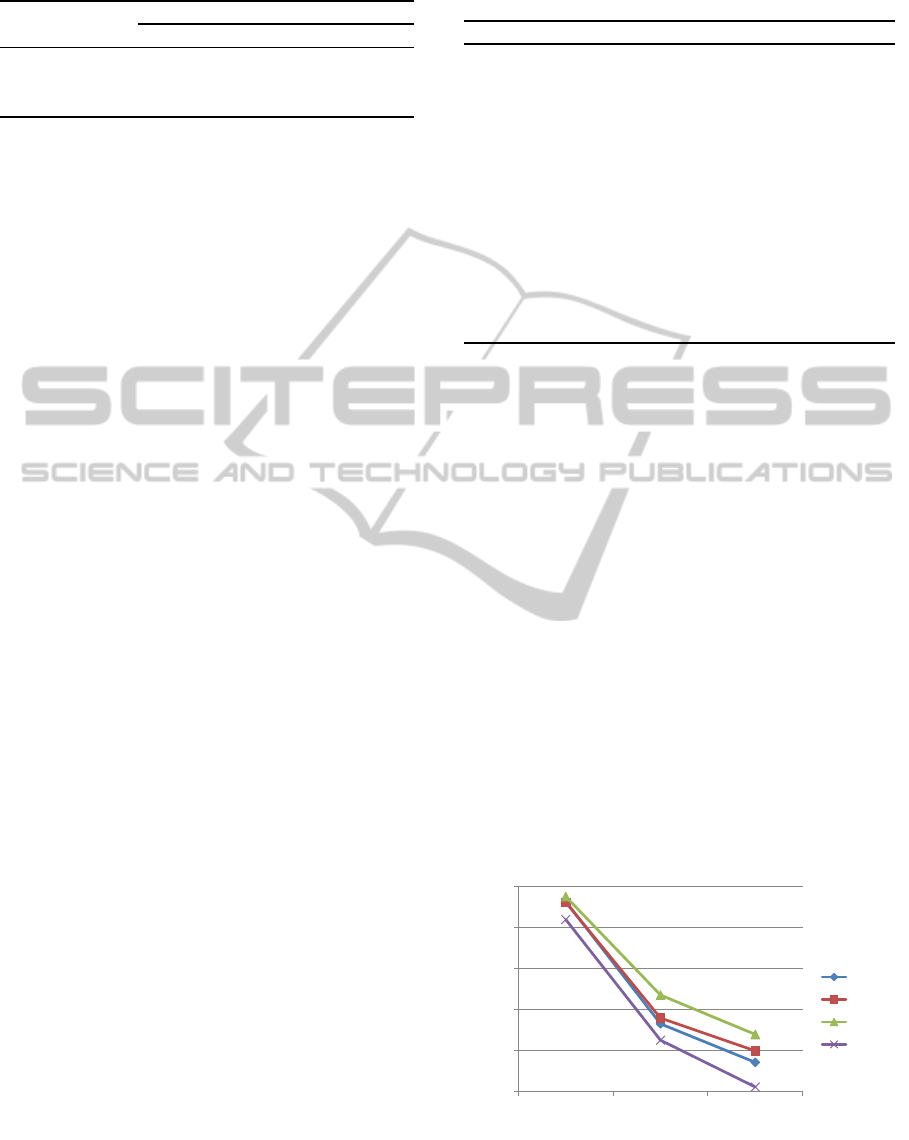
Table 2: Tuning the parameters of the SAILS.

value of k

temperature T 1 2 3 4

3 0.306 0.298 0.294 0.314

4 0.309 0.292 0.299 0.318

5 0.318 0.309 0.312 0.292

taken from Taillard (Taillard, 1993), with 120 in-

stances evenly distributed among 12 different sizes.

The scale of these problems varies from 20 jobs and 5

machines to 500 jobs and 20 machines. In the experi-

ment, ﬁve independent runs are performed for the in-

stances with less than 500 jobs. The ten instances with

500 jobs and 20 machines are run only once as they

are considerably more time consuming. For example,

for the terminal criterion 0.02n

m milliseconds CPU

time, about 13.9 hours are required for just one run.

The performance of the algorithms are tested us-

ing the relative percentage deviation (RPD), which is

calculated as:

RPD = (C −C

best

)/C

best

× 100 (7)

where C is the result found by the algorithm being

evaluated and C

best

is the best result provided by Pan

and Ruiz (Pan and Ruiz, 2012), found as the best so-

lution among their four proposed algorithms and 11

other state of the art works.

Each algorithm is implemented in C++, run-

ning on three similar PCs, each with an Intel Core2

Duo processor (2.99 GHz) and 2GB main memory.

Though each computer has two processors, only one

is used in the experiments, as no parallel program-

ming technique has been applied.

4.1 Tuning of the SAILS

There are two parameters in the proposed SAILS, the

ﬁrst one is k, used in Eq. (5); the other is the tem-

perature T, used in the self-adaptive perturbation (see

Fig. 2). The k is set to 1, 2, 3 and 4, respectively,

and the T is set to 3, 4 and 5, respectively. So there

are 12 combinations in total. The terminal criterion is

set to 0.02 × mn

. As it is too time consuming for the

500 jobs instances, the SAILS is only run on the ﬁrst

110 instances. The overall averaged RPDs (ARPD)

for these 12 combinations are listed in Table 2. From

this table, it can be seen that the results are quite sim-

ilar for each pair of T and k. However, the results are

generally better with k = 2. As the performance is

one of the best cases with k = 2 and t = 4, we choose

them in the following experiments.

Table 3: Comparison in ARPD for MRSILS, PR-ILS, PR-

IGA and SAILS (0.004n

m ms CPU time).

n|m MRSILS PR-ILS PR-IGA SAILS

20|5 0.007 0 0.016 0.007

20|10 0.002 0 0 0

20|20 0 0 0 0

50|5 0.476 0.558 0.485 0.501

50|10 0.575 0.677 0.630 0.584

50|20 0.534 0.610 0.589 0.393

100|5 0.824 0.888 0.819 0.834

100|10 1.032 0.941 1.127 1.022

100|20 1.076 1.043 1.171 0.991

200|10 0.740 0.754 0.667 0.750

200|20 0.393 0.283 0.296 0.293

500|20 0.121 0.020 0.063 0.149

Avg. 0.482 0.481 0.488 0.460

4.2 Evaluation of the SAILS

The values for the average RPD (ARPD) of all 120

instances are presented in Tables 3 - 5 for each com-

bination of n and m. From these tables, it can be seen

that SAILS generally performs the best. And with the

prolonging of CPU time, the superiority of the SAILS

increases (See Fig. 4). The reason for this is that the

self-adaptive strategy will be applied more times in

the search with prolonged CPU time, and then result-

ing signiﬁcantly better performance for the SAILS.

This also shows that the proposed strategy is effec-

tive, particularly with longer CPU time.

This phenomenon can also be observed on large

instances. With the 500 job instances, when the CPU

time limitation is set to 0.004×n

m, SAILS performs

the worst. When the CPU time limitation is set to

0.012×n

m, SAILS surpasses MRSILS and PR-IGA,

butis still worse than PR-ILS. With the CPU time lim-

itation set to 0.020×n

m, SAILS further outperforms

MRSILS and PR-IGA, and is quite similar to PR-ILS.

0.25

0.3

0.35

0.4

0.45

0.5

ρ=0.004

ρ=0.012

ρ=0.02

ARPD

CPU time limitation (ρmn

ms)

MRSILS

PR-ILS

PR-IGA

SAILS

Figure 4: Comparison results for the SAILS with the MR-

SILS, PR-ILS and PR-IGA with different CPU time set-

tings.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

382

Table 4: Comparison in ARPD for MRSILS, PR-ILS, PR-

IGA, SAILS (0.012n

m ms CPU time).

n|m MRSILS PR-ILS PR-IGA SAILS

20|5 0.007 0 0.007 0.007

20|10 0 0 0 0

20|20 0 0 0 0

50|5 0.345 0.406 0.279 0.363

50|10 0.398 0.494 0.572 0.462

50|20 0.388 0.431 0.537 0.303

100|5 0.646 0.703 0.678 0.650

100|10 0.766 0.739 0.897 0.751

100|20 0.841 0.836 0.853 0.738

200|10 0.547 0.597 0.527 0.536

200|20 0.083 -0.016 0.097 0.007

500|20 -0.027 -0.110 -0.034 -0.057

Avg 0.333 0.340 0.368 0.313

Table 5: Comparison in ARPD for MRSILS, PR-ILS, PR-

IGA, SAILS (0.02n

m ms CPU time).

n|m MRSILS PR-ILS PR-IGA SAILS

20|5 0.007 0 0.007 0.007

20|10 0 0 0 0

20|20 0 0 0 0

50|5 0.296 0.332 0.262 0.290

50|10 0.357 0.474 0.527 0.402

50|20 0.387 0.416 0.480 0.274

100|5 0.602 0.648 0.590 0.557

100|10 0.699 0.697 0.793 0.659

100|20 0.701 0.740 0.761 0.612

200|10 0.473 0.521 0.475 0.460

200|20 -0.002 -0.063 0.027 -0.046

500|20 -0.089 -0.165 -0.081 -0.144

Avg 0.286 0.300 0.320 0.256

5 CONCLUSIONS

Iterated local search algorithms are powerful for solv-

ing the PFSP minimizing total ﬂow time, with the per-

turbation method playing an important role. The MR-

SILS algorithm by Dong et al. (Dong et al., 2013) is

a state of the art ILS algorithm. However, one short-

coming is that the best current solution cannot be im-

proved in many local search runs during the search

process. Further, the perturbation method only moves

a randomly selected job to another randomly selected

position, without any bias, such that it is difﬁcult to

escape from a “deep” local optimum.

In order to overcome this shortcoming, a self-

adaptive perturbation method is proposed in this pa-

per. In this method, the search status is evaluated

by calculating the average objective value of a sam-

ple of the neighborhoods around the local optimum.

The greater the difference between the average ob-

jective value and the best current objective value, the

higher the probability that the perturbation strength

is increased and a randomly selected job is moved

to a position where worse solutions can be gener-

ated. The SAILS algorithm is proposed based on the

above analysis. Experimental results on benchmark

instances show that SAILS works quite well, espe-

cially for long CPU times. The proposed method-

ology developed here may potentially be applied to

other problems, as escaping local minimums with lo-

cal search is a difﬁculty for many combinatorial opti-

mization problems.

ACKNOWLEDGEMENTS

This work is supported by The Fundamental Research

Funds for the Central Universities of China (Project

Ref. 2014JBM034, Beijing Jiaotong University).

REFERENCES

Costa, W., Goldbarg, M., and Goldbard, E. (2012a). Hy-

bridizing VNS and path-relinking on a particle swarm

framework to minimize total ﬂowtime. Expert Systems

with Applications, 39:13118–13126.

Costa, W., Goldbarg, M., and Goldbard, E. (2012b). New

VNS heuristic for total ﬂowtime ﬂowshop scheduling

problem. Expert Systems with Applications, 39:8149–

8161.

Dong, X., Chen, P., Huang, H., and Nowak, M. (2013).

A multi-restart iterated local search algorithm for the

permutation ﬂow shop problem minimizing total ﬂow

time. Computers & Operations Research, 40:627–

632.

Dong, X., Huang, H., and Chen, P. (2009). An iterated

local search algorithm for the permutation ﬂowshop

problem with total ﬂowtime criterion. Computers &

Operations Research, 36:1664–1669.

Garey, M., Johnson, D., and Sethi, R. (1976). The complex-

ity of ﬂowshop and jobshop scheduling. Mathematics

of Operations Research, 1:117–129.

Johnson, S. (1954). Optimal two and three-stage production

schedule with setup times included. Naval Research

Logistics Quarterly, 1(1):61–68.

Liu, J. and Reeves, C. (2001). Constructive and composite

heuristic solutions to the p//

∑

scheduling problem.

European Journal of Operational Research, 132:439–

452.

Lourenc¸o, H., Martin, O., and St¨utzle, T. (2010). Hand-

book of Metaheuristics, volume 146 of International

Series in Operations Research & Management Sci-

ence, chapter Iterated Local Search: Framework and

Applications, pages 363–397. Springer US.

ASelf-adaptiveIteratedLocalSearchAlgorithmonthePermutationFlowShopSchedulingProblem

383

Nikolaev, A. G. and Jacobson, S. H. (2010). Handbook of

Metaheuristics, volume 146 of International Series in

Operations Research & Management Science, chapter

Simulated Annealing, pages 1–39. Springer US.

Pan, Q.-K. and Ruiz, R. (2012). Local search methods for

the ﬂowshop scheduling problem with ﬂowtime mini-

mization. European Journal of Operational Research,

222:31–43.

Pan, Q.-K., Tasgetiren, M., and Liang, Y.-C. (2008). A dis-

crete differential evolution algorithm for the permu-

tation ﬂowshop scheduling problem. Computers and

Industrial Engineering, 55:795–816.

Pinedo, M. (2001). Scheduling: theory, algorithms, and

systems. Prentice Hall, 2nd edition.

Rajendran, C. and Ziegler, H. (2004). Ant-colony algo-

rithms for permutation ﬂowshop scheduling to mini-

mize makespan/total ﬂowtime of jobs. European Jour-

nal of Operational Research, 155:426–438.

Rajendran, C. and Ziegler, H. (2005). Two ant-colony algo-

rithms for minimizing total ﬂowtime in permutation

ﬂowshops. Computers and Industrial Engineering,

48:789–797.

Ruiz, R. and St¨utzle, T. (2007). A simple and effective

iterated greedy algorithm for the permutation ﬂow-

shop scheduling problem. European Journal of Op-

erational Research, 177:2033–2049.

Taillard, E. (1993). Benchmarks for basic scheduling prob-

lems. European Journal of Operational Research,

64:278–285.

Tasgetiren, M., Liang, Y.-C., Sevkli, M., and Gencyilmaz,

G. (2007). A particle swarm optimization algorithm

for makespan and total ﬂowtime minimization in the

permutation ﬂowshop sequencing problem. European

Journal of Operational Research, 177:1930–1947.

Tasgetiren, M., Pan, Q.-K., Suganthan, P., and Chen, A.

H.-L. (2011). A discrete artiﬁcial bee colony algo-

rithm for the total ﬂowtime minimization in permu-

tation ﬂow shops. Information Sciences, 181:3459–

3475.

Tseng, L.-Y. and Lin, Y.-T. (2009). A hybrid genetic lo-

cal search algorithm for the permutation ﬂowshop

scheduling problem. European Journal of Opera-

tional Research, 198:84–92.

Tseng, L.-Y. and Lin, Y.-T. (2010). A genetic local search

algorithm for minimizing total ﬂowtime in the per-

mutation ﬂowshop scheduling problem. International

Journal of Production Economics, 127:121–128.

Xu, X., Xu, Z., and Gu, X. (2011). An asynchronous genetic

local search algorithm for the permutation ﬂowshop

scheduling problem with total ﬂowtime minimization.

Expert Systems with Applications, 38:7970–7979.

Zhang, Y., Li, X., and Wang, Q. (2009). Hybrid genetic

algorithm for permutation ﬂowshop scheduling prob-

lems with total ﬂowtime minimization. European

Journal of Operational Research, 196(3):869–876.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

384