A Holistic Approach to Railway Engineering Design

using a Simulation Framework

Jesus Carretero, Carlos Gomez, Alberto Garcia and Felix Garcia-Carballeira

Computer Science and Engineering Department, University Carlos III of Madrid, Avda. Universidad 30,

Leganes, Madrid, Spain

Keywords:

Simulation Framework, Optimization, Expert’s Knowledge, Productivity.

Abstract:

Simulators have become frequently used tools in railway infrastructure design. However, most of them could

be improved by adding capabilities to increase their productivity. In this paper, we propose a simulation frame-

work in the ﬁeld of railway infrastructure design, which allows to increase the productivity of simulators by

integrating as many aspects of the design process as possible. Also, we state that new generation simulators

should be capable of generating and evaluating new solutions by themselves. The framework follows a holistic

approach, focusing on four main issues: a) trade-off between accuracy and complexity; b) automatic gener-

ation and simulation of solutions; c) taking into account all parts in the design process (e.g. normative); and

d) integrating expert’s knowledge and optimization metrics. A case study is provided through a real-world

simulator of railway overhead air switches. The simulator is analyzed from the point of view of the proposed

framework, indicating how the different layers are fulﬁlled. Finally, the usability and productivity of the sim-

ulator is demonstrated performing an evaluation using different study cases. The evaluation shows how a high

number of scenarios are simulated, evaluated, and rated using optimization metrics, in order to ﬁnd the best

solution of the problem’s search space.

1 INTRODUCTION

Simulators are excellent tools to face new engineering

problems, testing different prototypes to develop op-

timal designs in an easy and economic manner. Sim-

ulators have been widely used in railways since the

past century (Brunner et al., 1998; Goodman et al.,

1998), but they have traditionally adopted the role of

solvers, calculating the physical, chemical or mathe-

matical equations associated to a particular engineer-

ing problem (e.g. FEM, CFD, etc.), which usually are

set by the user.

We state that new generation simulators should be

capable of, starting from a range of possible parame-

ters, proposing and evaluating new designs, and that

they should consider all issues that can affect to the ﬁ-

nal solution as part of its scope. Examples of such as-

pects are physical optimizations, normative,cost anal-

ysis, etc. We can resume this approach in four main

issues:

1. Trade-off between accuracy and complexity. The

simulator must evaluate a possible solution in the

lowest possible time. The results obtained must

be applicable to real world.

2. Automatic generation and simulation of possible

solutions. A simulator must be capable of propos-

ing and evaluating new solutions, exploring the

search space.

3. Other actors taking part in the design process (e.g.

legislation and normative) must be taken into ac-

count, to incorporate them into the simulator inso-

far as they inﬂuence the validity of the solutions.

4. Expert’s domain knowledge, useful to ﬁnd the

best solutions, must be also integrated into the

simulator, as well as optimization metrics.

These issues have a great impact on the complex-

ity and usability of the simulators, and should be con-

sidered carefully.

In this paper we introduce a simulation frame-

work which takes into account all the aspects that

can inﬂuence in the design process of engineering

solutions. This framework proposes an holistic ap-

proach, in which simulators can propose and evalu-

ate solutions, needing little or no interaction by the

user. Since those aspects (apart from the simulator’s

physical domain) which can inﬂuence the ﬁnal design

have been also taken into account, outcomes proceed-

Carretero J., Gomez C., Garcia A. and Garcia-Carballeira F..

A Holistic Approach to Railway Engineering Design using a Simulation Framework.

DOI: 10.5220/0005095400710082

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 71-82

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ing from this framework are more suitable to be im-

plemented in the real world.

In order to provide a study case, we illustrate the

proposed framework through a real-world simulator

in the ﬁeld of electric railways. We will analyze the

simulators characteristics, establishing a correspon-

dence to the different issues of the framework. The

aim of that simulator, presented in (Gomez et al.,

2012), is to design optimal conﬁgurations of over-

head line deployments on railway switches. Starting

from a set of parameters with regard to both infras-

tructure and train, the simulator generates different

deployments of the overhead infrastructure. For each

deployment, the simulator reproduces the pantograph

behaviour of the train running across the switch, tak-

ing into account pantograph and wire positions, cate-

nary geometry, tension of the wires, angles of attack,

and more. All these factors can inﬂuence the viability

of a solution, and thereby they must be considered.

Finally, the best deployment is selected, on the ba-

sis of several optimization metrics adopted from legal

normative and experts of the ﬁeld. Therefore, more

than solving a particular set of equations, the simula-

tor takes into account the whole design process.

The paper is structured as follows: Section 2 de-

scribes the simulation framework proposed. Section

3 analyses in detail the railway overhead air switch

problem. Section 4 describes the architecture of the

simulator, and how it corresponds to the proposed

framework. Section 5 evaluates the simulator, indi-

cating times spent on each one of the framework is-

sues. Finally, conclusions, ﬁnal remarks, and future

work are presented in Section 6.

2 SIMULATION FRAMEWORK

Railway infrastructures are considered critical sys-

tems, with requirements of efﬁciency, security and

safety, and hence they should be optimized. Nev-

ertheless, performing a high number of experiments

with real systems (tracks, locomotives, electric instal-

lations, etc.) is impracticable in terms of time and

money. The main goal of a simulator, in the ﬁeld

of railway infrastructure design, is to simulate experi-

mental designs or prototypesto evaluate if they are ac-

ceptable or not, or to provide a degree of ﬁtness. This

procedure is composed of several tasks: ﬁrst, a candi-

date solution must be selected, either being provided

by the user, or being generated by the simulator itself.

Then, the simulation is performed and the results are

analysed. The candidate solution is scored, and a de-

cision to accept it or reject it is taken. This proce-

dure is repeated across multiple ﬁelds in this area. In

railway dynamics, rail-vehicle interaction is analysed,

aiming to get new designs of rails and bogies which

may reduce wear and breakdowns. In overhead con-

tact line designs, structural behaviour (Nejlaoui et al.,

2013) of poles and portal frames are evaluated, check-

ing their feasibility (Saa et al., 2012). In the ﬁeld of

energy provisioning, a proposal of electric installation

locations may be simulated checking whether energy

is available to all planned trains (Abrahamsson et al.,

2013). (Hani et al., 2006) provides a simulation-based

optimization in order to provide the best building po-

sitions in a railway maintenance facility.

Although this general structure is present in most

railway infrastructure simulators, it may not be suf-

ﬁcient to grant an acceptable degree of productivity,

and should be enhanced. A simulator in railway in-

frastructure design must not be restricted to evalu-

ate solutions provided by the user, but also it should

ﬁnd acceptable solutions by itself, with a high degree

of ﬁtness, and in a reasonable amount of time. To

achieve these targets we present a simulation frame-

work, which allows to increase the output of simu-

lators by covering more capabilities than the main

procedure described before. Our enhancements are

focused on four main issues below addressed. The

sources of this approach are: railway company ex-

perts, railway infrastructure design and planning pro-

cesses described in (Kiessling et al., 2009), and previ-

ous works in this area made by the authors (Carretero

et al., 2003) (Saa et al., 2012).

First of all, a trade-off between accuracy and com-

plexity is required when designing a simulator. Pro-

ductivity issues in railway industry require not to

waste so much time when evaluating a single solu-

tion, as the design process may require to evaluate a

lot of candidate solutions. There is a relationship be-

tween the accuracy of the model and the complexity

of the simulation. On the one hand, accurate mod-

els are usually hard to simulate, and require more and

more operations, so the more accurate is the model,

the more complex it is, and the more time is needed

to reach the solution. On the other hand, accurate

models are likely to reproduce real results. Optimal

balance between accuracy and simulation may be dif-

ferent in different design processes, but we state that

an efﬁcient simulator should simulate and evaluate a

single candidate solution in the lowest possible time.

We state that an acceptable threshold to be productive

is to simulate and evaluate a candidate solution in less

than one hour.

In the second place, automatic generation and

simulation of solutions falls outside the scope of most

simulators. Therefore, the user must feed the simula-

tor providing new possible solutions, which leads to

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications































 

!

"

#

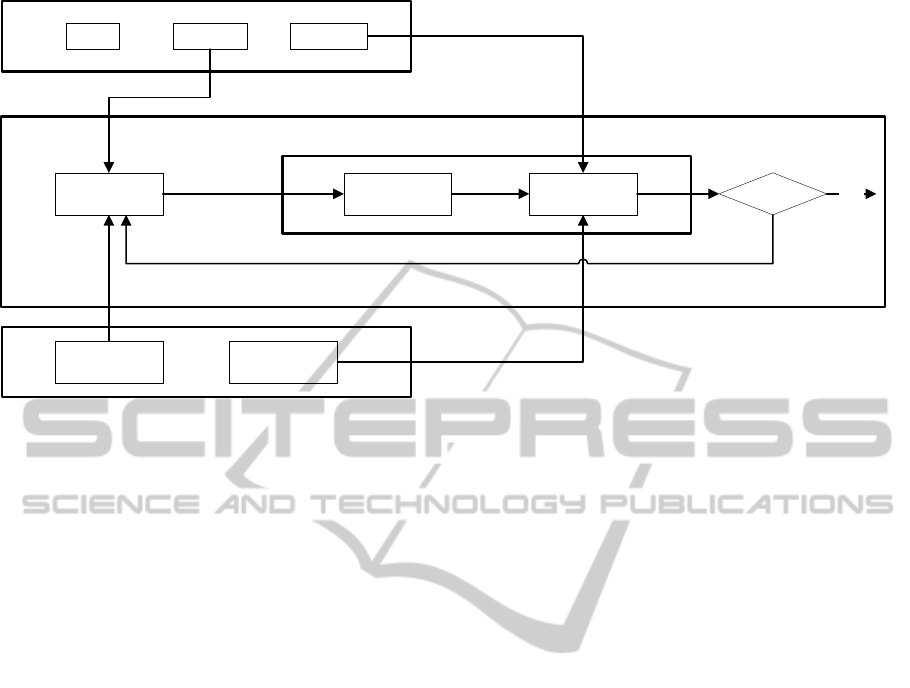
Figure 1: Simulation framework presented by the authors.

productivity losses. Moreover, the capacity of ﬁnding

good (maybe optimal) solutions is tied to the user and

her own ability to explore the problem’s search space.

We state that an efﬁcient simulator should evaluate

and simulate a set of solution with a minimal user in-

volvement. To achieve that: a) the user should pro-

vide the simulation parameters as a set of possible

values (e.g. [minimum, maximum, increment]), and

the simulator uses them to generate candidate solu-

tions; b) the simulator should be able to generate new

solutions starting from an initial database (e.g. an in-

ventory or catalogue).

Thirdly, there are many stakeholders taking part in

the design process which usually fall out of the scope

of the simulation models. These parts can inﬂuence,

or even determine, the ﬁnal acceptance of the candi-

date solutions (Naweed et al., 2013). For instance, the

set of possible solutions when looking for a valid de-

sign of a railway portal frame, can be limited by the

availability of constructive pieces in the company’s

inventory, and once found, a portal frame that stands

could not be in compliance with legal normative in

certain countries (BS-EN-50119, 2009). All issues

that have to be considered throughout the design pro-

cess, but fall out the scope of the simulation model,

should be also taken into account when simulators

generate and evaluate candidate solutions. This cat-

egory includes provider speciﬁcations, client require-

ments, technical security, and legal normative. Differ-

ent ways to include such restrictions out of the simu-

lation model are: a) restrictions to generate candidate

solutions: the simulator only generates candidate so-

lutions that fulﬁll with these initial restrictions; b) re-

strictions to evaluate a candidate solution, so that the

simulator evaluates these restrictions as well as any

others conditioned by the simulation model.

Finally, expert’s domain knowledge is a funda-

mental part in the engineering design process (Adeli,

2003). Expert’s knowledge deﬁnes as heuristics that

allow to speed up the search process and achieve the

best solutions in the problem’s search space. There-

fore it should be included as a part of the simula-

tion, particularly in those simulators that include au-

tomatic generation of candidate solutions (described

as the second issue). In a similar way to other par-

ticipants in the design process, expert’s knowledge

can be included when generating candidate solutions

in the form of decision rules. Those rules guide the

search process to generate better candidate solutions.

They can also be included to evaluate a candidate so-

lution in the form of optimization metrics, that can

be used to score the solution and to compare it with

others, thus choosing the best one.

The proposed framework is showed in Figure 1.

This ﬁgure is layered following the four issues previ-

ously mentioned. The core procedure of simulating

and evaluating candidate solutions composes layer 1.

Time invested in performing these two tasks must be

the lowest possible. Issue 2 is covered by the layer 2,

which contains the task of generating automatically

new solutions to be evaluated. This task could be fed

from other elements in layers 3 and 4 (e.g. require-

ments related to an inventory of constructive pieces,

or expert’s domain knowledge, applied to generate

better candidate solutions). Layer 3 is composed by

those restrictions that are not included in the simula-

tion procedure (layer 1), but that have an impact on

the solution. Those restrictions can be applied either

when generating or when evaluating a candidate so-

lution. Examples of such restrictions are availability

AHolisticApproachtoRailwayEngineeringDesignusingaSimulationFramework

of constructive pieces in company’s inventory when

proposing a design, or compliance with legal norma-

tive when evaluating the proposed design. Finally,

layer 4 represents the expert’s domain knowledge that

allows to obtain better solutions. Decision rules used

to generate better candidate solutions, or optimization

metrics used to choose the best one, are included in

this layer. This approach improves the efﬁciency of

the simulators by giving them the ability of searching

for the best solutions in the problem space. Obtained

solutions will be fully-integratedwith the different ac-

tors of the design process, and therefore they are more

suitable to be implemented in the real world.

3 CASE STUDY: OVERHEAD

LINE AIR SWITCHES

Overhead lines have become the way to provide en-

ergy to high speed trains. Apart from the signiﬁcant

advantages over other mechanisms such as a third rail,

overhead lines are the only alternative when dealing

with high voltages (25.000 V) like those used in high

speed railways. Nevertheless, overhead lines require

to maintain the contact between pantograph and the

wire, in order not to break energy supply to the train.

This suppose an engineering challenge when the train

is moving along the main tracks (geometry, catenary

dynamics, wearing down, etc.).

When a train takes a switch in order to change to

other track, even more difﬁculties arise. The panto-

graph has to lose contact with the outgoing catenary

of the straight track, and make contact with the in-

coming catenary of the diverging track. On the one

hand, transition between overhead lines must be con-

ducted without losing contact with at least one of the

wires, in order not to interrupt power supply to the

train. On the other hand, the change must be per-

formed gently, in order to avoid excessive wearing or

breakdowns.

The task of designing an overhead line air

switches is a complex problem since several ele-

ments with different parameters must be considered.

(Kitchin and Holland, 1950) discusses the problems

to be faced by the designers of overhead equipment

for the electriﬁcation of railways. Some research

about the integration of catenaries and switches is pre-

sented in (Kiessling et al., 2009).

A standard catenary is composed of a messenger

wire holding a contact wire that supplies the elec-

tric power to the pantograph of the train. Both wires

are hung at a speciﬁc tension and are attached to

each other at regular intervals by drop wires. These

droppers are responsible for maintaining the contact

wire hung at a constant height with a slight deﬂec-

tion. Hence an uniform contact between the panto-

graph and the wire as the train travels along the track

is possible, thus avoiding any notches due to the pan-

tograph thrust force. In addition, contact wires must

be zigzagged slightly to the left and to the right of

track axis so that the pantograph wears evenly its fric-

tion surface. This stagger is a critical issue to be ana-

lyzed in the problem presented.

We focus on the critical study case of railway

switches, where a train travelling along the straight

track has to change to the diverging track. In this kind

of problem, two different catenaries are needed to

guarantee the electricity supply to both tracks, the left

side of the Figure 2 shows a real example of tangen-

tial overhead line air switches. Therefore, there will

be overlapped spans along the switch stretch length.

The right side of Figure 2 shows the conﬁguration of a

overhead line air switch. As may be seen, the diverg-

ing track elevation span allows to lower the contact

wire height, so that the pantograph can progressively

change the rubbing wire while moving forward. The

beginning of this change takes place at a characteris-

tic pointCp where the heights of both elevation spans

match (see the right-up side of Figure 2). From this

point on, the pantograph will interact with the con-

tact wires of two different catenaries. Next, in the

switching span, both catenaries are gradually separat-

ing. This allows the pantograph to lose the contact

with the outgoing catenary and to get contact with the

incoming catenary.

The conﬁguration of an overhead air switch poses

a set of restrictions to be ensured along the train tra-

jectory on the railway switch:

• When the train travels over the straight track, the

pantograph should only rub the contact wire of

this track. This avoids an excessive wear and tear

of the diverging track contact wire, that may result

in breakdowns and economical costs.

• Other possible ﬂaw points to be analyzed, may oc-

cur when the train is travelling along the diverg-

ing track. Firstly, as the entire pantograph surface

is not suitable for making contact with the con-

tact wire, the pantograph should start rubbing it

over its central part, called friction surface. Sec-

ondly, the beginning of the rub should be smooth

and progressive. A hazardous breakdown of the

catenary or the pantograph may occur otherwise.

• Regardless of the track to be simulated, it is es-

sential that the pantograph is always rubbing one

of the contact wires, so that there is no electricity

notches affecting the train movement.

The number of combinations of catenary infras-

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

1 42

El (Elevation span)

Sl (Switching span)

Tracks

Straight track catenary

Diverging track catenary

junction

1 4

Figure 2: Photography of a real air switch and schemes (ground and elevation views).

tructure geometry for a single air switch may vary

between a few thousand and more than one million.

Each one of these combinations is a possible solution

of the design problem.

4 SIMULATOR ARCHITECTURE

This section describes the air switch simulator in

terms of the proposed framework described before.

The aim is to illustrate how a real-world simulator can

be adapted to the framework and the enhancement in

usability and productivity obtained through the adap-

tation. We start by describing the simulation model,

the core of the simulator in which one single scenario

is simulated and evaluated. Next, we analyse all lay-

ers of the framework and how they are reﬂected in the

simulator.

4.1 Simulation Model

The complete simulation model is described in

(Gomez et al., 2012), including all the equations

which determine output data. The model starts from

three main sets of input data which correspond to the

two key factors in an overhead line air switch: the

switch scheme and a candidate overhead line deploy-

ment, and the environmental conditions in which the

simulation is carried on:

• The switch scheme determines the trajectory of

the train across the rails, and therefore the posi-

tion of the pantograph on each instant. Based on

these data and trigonometry equations, the angle

at any point of the switch axis can be obtained,

thus allowing to simulate the pantograph position

when travelling along the switch.

• Overhead line deployment conﬁguration deter-

mines characteristics of the contact wires across

the switch. It can be divided in two groups: cate-

nary geometry, which indicates the position of the

wires, and catenary installation features, which

deﬁnes catenary behaviour when the pantograph

makes contact with it.

– Catenary geometry contains the parameters re-

lated to the modelling of the ground plan and el-

evation of the catenary, i.e., its geometry. How-

ever, catenary geometry can support multiple

conﬁgurationsthat are allowed for the givende-

sign problem. For example, one solution may

be feasible whether the junction point is 90 or

120. These different conﬁgurations deﬁne the

multiple solutions for the design problem.

– Catenary installation features deﬁnes physical

characteristics of the catenary (stiffness, deﬂec-

tion, tension), which may affect the way the

pantograph makes contact with the wires. For

instance: a more rigid catenary is less sensitive

to displacements provoked by pantograph iner-

tia, but it is prone to breakdowns due to wear

and tear.

• Finally, a third set of input parameters is simu-

lation conditions data, which contains those en-

vironmental conditions apart from the rail switch

and catenary data (i.e. wind speed and direction,

trains speed, etc.).

With these data, the pantograph-catenary interac-

tion along the switch is simulated. Pantograph trajec-

tory across the switch is divided in simulation steps.

The simulator calculates the position of the panto-

graph referring to the contact wires on each step for

each simulation step of the scenario. Figure 3 illus-

trates all the stages followed by the simulator, that are

AHolisticApproachtoRailwayEngineeringDesignusingaSimulationFramework



























































































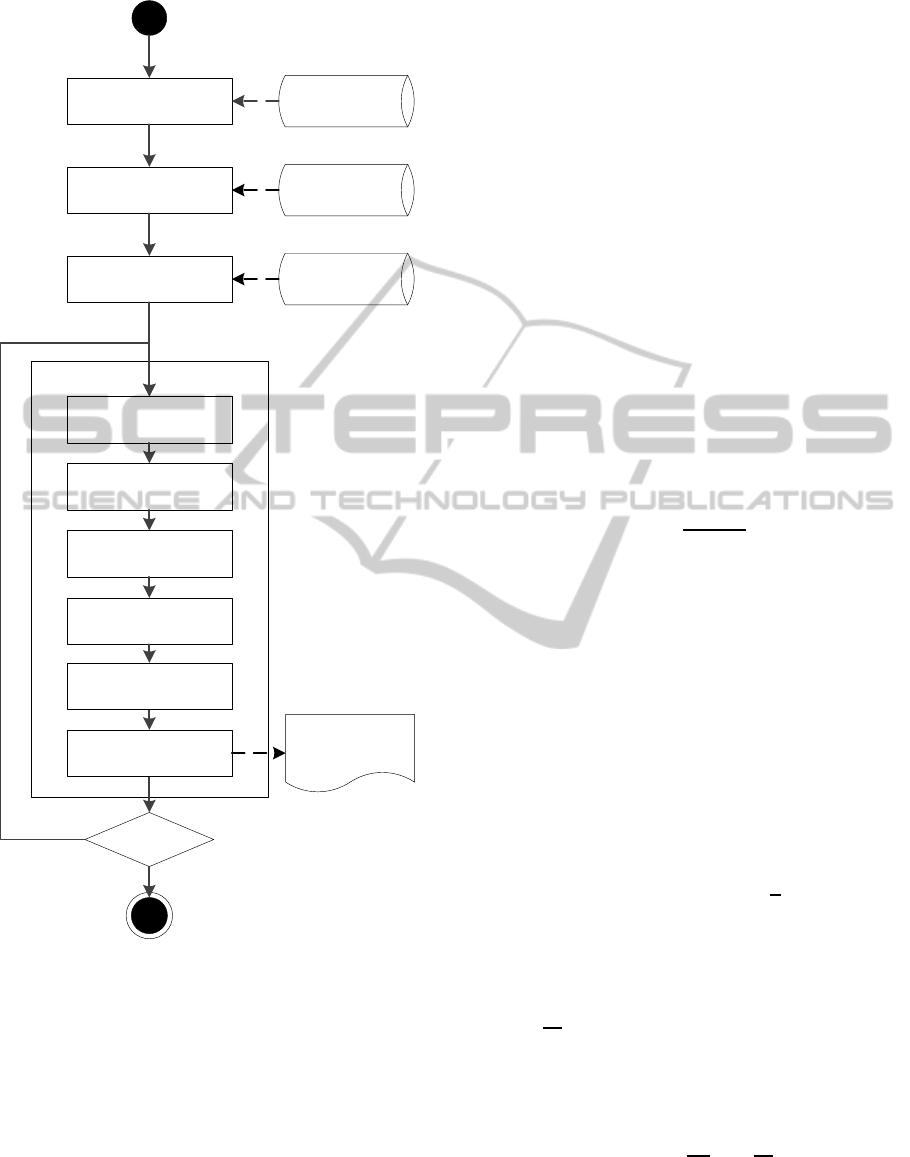
Figure 3: Simulation model and its stages.

stated below.

1. Compute pantograph position. First, pantograph

position k

is computed for each simulation step i

by increasing the former pantograph position in

the track with the pantograph displacement de-

ﬁned (see Equation 1). For the ﬁrst step, the initial

position is set to the position of the ﬁrst pole of the

switch infrastructure k

= k

i−1

+ δ

(1)

2. Compute contact wires position. Second step is

computing contact wires position. This step is

in charge of calculating the position of the con-

tact wires accurately for the pantograph position

at this simulation step. Equation 2 is applied along

the span to compute the base wire height for that

point.

) =







H k

< d

H − deflection(k

) d ≤ k

< l − d

H k

≥ l − d

(2)

where d is the distance from the beginning of the

span to the ﬁrst dropper, and l is El or Sl, depend-

ing on whether the current span is the elevation

span or the switching span. Equation 3 is used to

compute wire deﬂection at each point, being D

max

the maximum deﬂection deﬁned as an input pa-

rameter.

deflection(k

) =



(l − d) · (k

− d) − (k

− d)





4·

max

(l − d)



(3)

3. Apply environmental conditions. Depending on

the simulation conditions deﬁned by the input pa-

rameters, wire stagger could be modiﬁed due to

several environmental aspects. Equation 4 is used

in our simulator to include the transversal wind

force. The equation computes the horizontal dis-

placement of the contact wire due to wind effects

in standard conditions (15 degrees and 600 meters

over the sea).

= Pv

ContWire

+ Pv

MesWire

(4)

where

Pv = q

·G

·dWire being q

·G

·ρWs

reﬂects the wind burst, with a value of 2.05, as

deﬁned by the standard ENV 1991-2-4:1995 (see

page 42 in (BS-EN-50119, 2009)), G

is a terrain

factor, Ws is the wind speed, ρ is a factor equal to

1.225

, and dWire is the diameter of the wire,

obtained from its section area A. Equation 5 is

applied to calculate wire contact horizontal dis-

placement:

) =









(5)

where W

is the resulting wind force and T is

the tension due to the catenary. The result is a

quadratic curve, similar to the wire deﬂection.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

4. Determine pantograph height. Once calculated

the contact wire positions, the pantograph height

must be computed for this simulation step as fol-

lows. Since there are two catenaries, for the main

and the diverging tracks, the pantograph height

will be the minimum height of the wires that are

within the projection of its friction surface, i.e.,

the rubbing contact wire will be the lower one. If

both wires are out of the friction surface projec-

tion, then the pantograph height will be consid-

ered as ∞ to indicate an error.

5. Modify contact wire elevation and angle. The ﬁfth

step is modifying contact wire elevation and an-

gle due to the pantograph interaction. Some pa-

rameters needed, such as elasticity in the center

of the catenary spans and in the cantilevers, are

received as input parameters in the catenary in-

stallation features. Train speed Ts, must also be

considered. In order to know the elevation, the

pantograph pressure over the wires must be com-

puted, as shown in Equation 6 that follows ETI

regulation (ETI, 2008).







0.00097· Ts

+ 70 Ccs is A.C.

0.00097· Ts

+ 110 Ccs is D.C. 3.0 kV

0.00228· Ts

+ 90 Ccs is D.C. 1.5 kV

(6)

Next, the elasticity is computed for the catenary

point using Equation 7, where the denominator is

the stiffness at that point.

E(k

) =



1− αcos



2πk



(7)

where

max

+ K

min

and α =

max

− K

min

max

+ K

min

The elevation of the contact wire due to the pan-

tograph is obtained using Equation 8.

e(k

) = E(k

) · F

(8)

After determining the elevation produced by the

pantograph, the deﬁnitive contact wire height

must be computed as expressed in Equation 9.

) = y

) + e(k

) (9)

Thus, the contact wire position at a kilometric

point k

can be deﬁned as the following tuple:

W p

) = (st

) + w

),y

)) (10)

55000

60000

65000

70000

75000

80000

85000

-2000

-1500

-1000

-500

500

1000

5200

5250

5300

5350

5400

Straight track contact wire

Diverging track contact wire

Pantograph plane

Kilometric points (k

)

Stagger (st

)

Figure 4: Simulation graphic representation.

6. Write results. Last step is logging results to ﬁle.

Once computed all the signiﬁcant parameters, the

target output data of the simulation step are writ-

ten to the simulation scenario log ﬁle.

The simulator provides the following output data:

• Kilometric point where an iteration of the simula-

tion algorithm has been executed.

• Output data of the catenaries belonging to the

straight track and the diverging track respectively,

including elevation, stagger, height, angle, etc.

• Switching distance at this simulation kilometric

point. It increases as moving forward along the

switch.

• Identiﬁcation of what catenaries (straight, diverg-

ing, or both) are rubbed by the pantograph.

Having all these output data will allow to repro-

duce the simulation results a posteriori using a graph-

ical representation of the simulation. This represen-

tation shows relevant data displaying the pantograph

run, wire positions, alarms, etc., and can help to pro-

vide users relevant information. An example of this

representation is shown on Figure 4.

4.2 Evaluation Rules

Once simulated, a solution have to be evaluated in or-

der to decide a) if that solution is feasible, and b) if

that solution is a ”good” (maybe optimal) solution.

Evaluating a solution is carried out by a rules engine,

which applies a certain number of rules over the out-

put results obtained from the simulation. These rules

can be catalogued in different categories.

From domain speciﬁc restrictions (sine qua non

conditions), to different aspects involvedin the design

process beyond the simulation model scope, the rules

engine allows us either to mark a solution as valid

or not, or to score the solution indicating a degree of

AHolisticApproachtoRailwayEngineeringDesignusingaSimulationFramework

goodness. Domain speciﬁc restrictions, as part of the

simulation model, will be described now, while ad-

ditional rules coming from other actors in the design

process will be discussed on sections 4.5 and 4.6.

The following are domain restrictions inherent in

the simulation model. More than to normative, eco-

nomic aspects, or other parts, they are related to the

physical issues of the problem, such as maintaining

the power supply, avoiding breakdowns, etc.

1. The contact wires do not interact with the panto-

graph, so overhead line is not supplying the train

with energy.

2. The stagger of any of the wires interacting with

the pantograph is larger than a half of the panto-

graph friction surface. Usually pantographs are

designed to rub against the wire in a speciﬁc

strengthened zone, located at the middle of the

pantograph. In order to avoid breakdowns, con-

tact wires cannot make contact with the panto-

graph outside this zone.

3. Contact wires of straight and diverging tracks in-

tersect. Since different centenaries can be fed by

different power stations, accidental contacts be-

tween contact wires can produce short-circuits.

4.3 Layer 1: Trade-off between

Accuracy and Complexity

Time spent on simulating one single scenario is a crit-

ical issue with regard to simulator’s usability and pro-

ductivity. Furthermore, the more accurate a simula-

tion is, the longer the time required to carry on with it

will be. When simulating overhead air switches, step

size determines the detail level of the simulation. In

order to obtain results as real as possible, simulations

have to be carried out by millimetre-steps. By this

way, pantograph and wires output data are more ac-

curate. On the other hand, more steps imply more

computing resources, performing more calculations

in order to obtain a larger amount of output data.

For each simulation step, the processor has to

solve the equations shown before. Modern CPU

cores can perform millions of operations per seconds,

which implies no more than a millisecond spent on

solving simulation steps and writing output data to

ﬁles. The problem is that the largest railway switches

may have a length up to 1000 metres. This im-

plies that a scenario may require about one second

to be simulated (using steps of one millimetre). This

amount of time is acceptable when dealing with just

one single scenario, but when dealing with thousands

or millions of scenarios (see further sections) high-

performance techniques are necessary to run different

simulations concurrently, taking advantage of multi-

core or multi-processor systems.

4.4 Layer 2: Generation and Evaluation

of Possible Solutions

As previously mentioned, we state that an efﬁcient

simulator should evaluate and simulate a set of solu-

tions with a minimal user involvement. New genera-

tion simulators should be capable of, starting from a

range of possible parameters, proposing and evaluat-

ing new designs. The proposed framework aims this

objectivethrough introducing a new component in the

simulator.

This component is a scenario generator, which

wraps the simulation model (simulation and evalua-

tion of one single scenario) generating different solu-

tions to be evaluated. This component generates new

scenarios through variations on the input data, thus al-

lowing experimentation with different simulation pa-

rameters, different components, or different domain

restrictions. Those scenarios are provided to the sim-

ulation engine, which carries on with the simulation

as described in the previous section.

Generating and evaluating multiple scenarios au-

tomatically allows the simulator to test different so-

lutions, thus providing a faster way of exploring the

solution space. Rather than obtaining one single so-

lution, by this way a set of feasible solutions is ob-

tained, and the user can select the best one. More-

over, as will be described in Section 4.6, enhancing

the simulator with optimization metrics or some ex-

perts knowledge brings the opportunity of performing

an automatic guided search of the solution space.

In order to cope with this issue, our simulator im-

plements a new module, accountable for generating

multiple scenarios. In order to do this, we change the

input data deﬁnition. With regard to the simulation

model, input parameters are transformed from scalar

values (e.g. train speed Ts = 220 km/h) to an inter-

val of test values deﬁned by the user, who speciﬁes

a maximum, a minimum, and a delta variation. Let P

an interval parameter,P = {P

min

≤ P

max

min

+ j · ∆P; j ∈ N

∗

}. By this way we deﬁne a com-

plete set different values, and different simulations

each one using a differentvalue of this parameter have

to be performed.

Of course, introducing variations in several pa-

rameters at the same time increases the number of sce-

narios exponentially, since we have to perform com-

binations with elements of the two (or more) sets. An

advantage of this explosion is that the solution space

is rapidly explored, evaluating a huge number of solu-

tions from the problem space. As a drawback, a large

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

amount of computing power is required to perform a

large number of simulations, so the trade-off between

accuracy and complexity previously mentioned has

great signiﬁcance. In this particular case, the number

of combinations of catenary conﬁguration parameters

can reach over one million. Each one of these combi-

nations is a possible solution of the design problem.

In order to carry out the search efﬁciently, multiple

scenarios can be simulated concurrently, dispatching

simulation kernels performing different scenarios to

different CPUs. In Section 5, an illustrative example

will be shown, indicating input parameters variation,

number of scenarios generated, evaluated, and time

consumed in simulation.

4.5 Layer 3: Other Actors

The amount of scenarios outputted from the previous

layer would be unmanageable by the user if no more

ﬁltering is applied apart from the physical domain re-

strictions. In order to increase the functionality and

productivity of the simulator, we have to take into

account the different stakeholders which take part in

the design process. Different determining factors may

fall into this category: legislation and normative, cost

limitations, provider or client restrictions, available

stock, and so on. There are two ways of consider-

ing such participants. The ﬁrst is enhancing the set of

evaluation rules, checking not only physical domain

restrictions, but also speciﬁc restrictions from differ-

ent sources. The second is restricting values of the

input parameters, limiting the generation of new sce-

narios to only those which may comply with those

restrictions.

Our simulator may take into account different nor-

mative currently in force. So additional evaluation

rules have been implemented in order to check if a

solution is feasible or not, counting:

• Normative EN-50119 (BS-EN-50119, 2009).

This normative stipulates different restrictions

with regard to overhead line deployment (mini-

mum and maximum height, droppers conﬁgura-

tion, etc.). Moreover, it stipulates different restric-

tions about the way the pantograph makes contact

with the wires.

• Normative EN-15273 (BS-EN-15273, 2009).

This normative stipulates maximum width and

headroomin railway lines, stating that certain area

around the rails have to be free of obstacles. This

restriction has effect in the way the overhead lines

are deployed.

4.6 Layer 4: Expert’s Knowledge

Even if additional restrictions from other actors are

considered to ﬁlter the number of feasible solutions,

the resulting set might be too large to be useful. Be-

sides, the user doesn’t know what solutions are better

than the others. Expert’s knowledge can be applied

in order to discriminate, from the set of feasible solu-

tions, what are the best ones. In order to do this, ﬁrst

of all we have to declare what optimization metrics

are going to be followed, i.e. the criteria that deter-

mines if a solution is better than other. Then, that cri-

teria can be applied by two ways: the ﬁrst is enhanc-

ing the set of evaluation rules with a new set of rules

which don’t check the feasibility of the solution, but

score the solution following the proposed criteria; the

second is modifying again the generation of new sce-

narios trying to seek those scenarios that best ﬁt with

the proposed criteria, in the same way as MOEAs

(MultiObjective Evolutionary Algorithm) try to reach

the optimal solution. The ﬁrst approach may lead to

an exhaustive search in the solutions space, but as

drawback, all solutions must be simulated. The sec-

ond approach saves time by driving a guided search,

but a number of solutions can remain ”untested”.

With regard to our overhead air switch simulator,

several optimization metrics have been chosen. The

issue of getting such a solution for the overhead air

switch design problem is not deﬁned by any regula-

tion, i.e., it is still an open research topic. We have

closely cooperated with railway experts to deﬁne the

metrics to be used, thus including that knowledge

within the simulator. Some example rules are shown

below:

1. Maximizing the average distance between contact

wires of straight and diverging tracks. It forces the

wires to be as far apart as possible. This will avoid

potential problems due to high electrical voltages

ﬂowing through the wires.

2. Minimizing the variance of stagger of the diverg-

ing track contact wire. This metric is intended to

avoid too many sudden changes of position of the

contact wire on the pantograph.

3. Minimizing the average symmetry between con-

tact wires of straight and diverging tracks. It mea-

sures the difference between the stagger of both

contact wires, which are sought to be as symmet-

rical as possible to the axis of the pantograph,

thus avoiding a pantograph tilt towards one of the

sides.

4. Minimizing the input angle of the diverging track

contact wire in the pantograph along the transi-

tions STI-BTI. This angle is intended to be as low

AHolisticApproachtoRailwayEngineeringDesignusingaSimulationFramework

Figure 5: Simulation architecture following the proposed framework.

as possible, thus avoiding a sharp blow on the pan-

tograph. By smoothing the entry of the contact

wire in the pantograph, damages and premature

wear of the wire can be decreased.

5. Minimizing the output angle of the straight track

contact wire out of the pantograph along the tran-

sitions BTI-DTI. This angle is desired to be as

low as possible, thus avoiding a sharp blow on the

pantograph. This metric is particularly important

when simulating a train the other way around, i.e.,

from the diverging track to the straight track.

6. Minimizing the average of stagger of the diverg-

ing track contact wire. This metric ensures that

the diverging track contact wire is as focused as

possible to the axis of the pantograph, thus avoid-

ing the approximation of the thread to the edges of

the pantograph and ensures that the contact wire is

always going to enter a valid area.

The ﬁrst metric is maximized, butthe overallfunc-

tion, that includes all the metrics, must be minimized.

To resolve this conﬂict, we change the sign of the ﬁrst

metric value so as to normalize the result. In order to

compute the overall function, we use a speciﬁc weight

to confer greater or lesser importance on each metric.

At the end, the optimal scenario is the one that mini-

mizes the overall function value. Since there are met-

rics inversely correlated, it is impossible to ﬁnd a sce-

nario having the best value per metric, being possible

to have a scenario better in some metrics and worse

in other ones. According to this fact, the framework

ﬁnds best scenarios considering an overall function of

all metrics, following a Pareto frontier.

Figure 5 describes the global architecture of the

Table 1: Parameters of the study cases.

Study case Radius Max. speed Type

1 250 m 20 km/h Former installations

2 500 m 60 km/h Non high-speed

3 1500 m 100 km/h High-speed

simulator, adapted to the proposed framework. The

simulation model is composed of the simulation and

evaluation components. A generation engine pro-

duces different scenarios to be tested, dispatching

simulations concurrently to any CPU available. Data

proceeding from other actors and expert knowledge

feed both generation and evaluation engines, in order

to reduce the amount of generated scenarios, ﬁlter the

number of feasible scenarios, and calculate the degree

of goodness in order to obtain the best ones.

5 EVALUATION

In this section we perform an evaluation of the over-

head air switch simulator using three different study

cases. A brief description of that study cases is pre-

sented in Table 1.

We have selected three types of switches, depend-

ing on the maximum allowed speed of trains run-

ning along the switch. The ﬁrst study case is a small

switch with a short radius (the shorter the radius is, the

slower the train has to run along the switch). These

switches are used in old stations, legacy of former

installation. Due to its closed curve, these switches

should be crossed at low speed. The second study

case is a regular switch used in modern non-high

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

Table 2: Computing time and number of solutions generated and simulated.

Case Mode Scenarios generated Scenarios discarded Final set Generation time (s) Simulation time (s) Evaluation time (s)

Parallel

55440 54944 5 6

243

Sequential 1067

Parallel

81900 81750 5 8

960

Sequential 3548

Parallel

126000 125700 5 12

1789

Sequential 6510

speed tracks. Finally, the third study case is a high

speed switch.

Once all the study cases have been presented, we

analyse the results from two different points of view:

a performance analysis in terms of computational ef-

ﬁciency, and an analysis of the adaptation between

the proposed framework and the described simulator.

All the experiments have been carried out in a Linux

workstation with an Intel Core i5 760 2800 MHz, 4

CPU cores, and 16GB of RAM. We have used a MPI

version of the simulator dispatching one MPI process

per core.

Table 2 shows the workload distribution across the

different stages of the framework. It also indicates

the number of scenarios generated, evaluated, and dis-

carded. Following the proposed framework, most of

the computing time is spent on simulating and to a

lesser extent evaluating solutions. The remainder of

the computing time is spent on generating all the sce-

narios. In order to analyse the performance we have

calculated the speed-up, which shows the time im-

provement provided by concurrent simulation of sce-

narios when using a multi-core computer. The aver-

age speed-up calculated among all the study cases is

3.90. It can be seen that the parallel execution out-

performs sequential execution. This is because, as we

state on Figure 5, the simulator allows to dispatch sce-

narios to different cores of the CPU, carrying on sim-

ulation and evaluation stages concurrently. Provided

that all study cases have been test in a four-core CPU,

the calculated speed-up value is nearly the theoreti-

cal one (4). This implies the absence of bottlenecks

and a high degree of scalability with regard to to the

number of scenarios simulated. Only the generation

stage is not carried out concurrently, which represents

the remaining 0.1 between calculated and theoretical

speed-ups.

After analysing the performance, we focus on the

adaptation to the proposed framework. The character-

istic points are marked below:

• Generation of different scenarios by combining

the interval parameters is implemented as a rules

engine within layer 2.

• Normative EN-50119 and EN-15273 are imple-

mented as evaluation rules in layer 3, along with

physical domain restrictions described in Section

4.2. All are applied in the evaluation step.

• A high number of solutions are generated by vari-

ation of input parameters in all study cases. Nev-

ertheless, most of them are discarded by physical

criteria or normative. The ﬁnal set of feasible so-

lutions is ordered through applying optimization

metrics deﬁned in Section 4.6, leaving the user to

analyse only 5 scenarios out of the thousands that

compose the problem space.

6 CONCLUSIONS

In this paper, we have presented a simulation frame-

work with the aim of enhancing functionality and pro-

ductivity of simulators in the ﬁeld of railway infras-

tructure design. This approach is focused on four

main issues: trade-off between accuracy and com-

plexity, automatic generation and simulation of pos-

sible solutions, taking into account other participants

in the design process, and integrate expert’s domain

knowledge and optimization metrics. This structure

improves the efﬁciency of the simulators by giving

them the ability of searching for the best solutions in

the problem space. Also, obtained solutions will be

fully-integrated with the different actors of the design

process.

A case study is provided in the form of a rail-

way overhead air switch simulator. We describe the

problem and the current simulation model which re-

produces the pantograph run across the air switch.

Starting from this simulation model, more layers have

been added following the proposals of the simulation

framework. As a result, the simulator provides a set

of feasible solutions, in accordance with current nor-

mative, and sorted by a degree of goodness provided

by expert in the ﬁeld. Evaluation results show how a

huge amount (tens of thousands) of scenarios can be

tested, obtaining a reduced set of feasible solutions,

and grading these solutions using optimization met-

rics. Time to simulate and evaluate all scenarios has

been less than two hours in the works case.

As future work, we will analyse in more detail the

simulation framework. A main guideline is to propose

AHolisticApproachtoRailwayEngineeringDesignusingaSimulationFramework

a complete IDE, in which the user can customize all

elements described in this paper (simulation model,

evaluation rules, experts knowledge, etc.). Besides,

several efforts are currently in progress in order to

adapt the framework to modern computing paradigms

such as cloud computing. Finally, other future work

will be to extend the framework, from the limited do-

main of railway infrastructure design to a broad do-

main of simulation in engineering. Concepts in rail-

way infrastructure design are quite similar to other

engineering domains, (civil engineering, chemistry)

so the proposed framework could ﬁt with these other

domains.

REFERENCES

Abrahamsson, L., stlund, S., Schtte, T., and Sder, L. (2013).

An electromechanical moving load ﬁxed node posi-

tion and ﬁxed node number railway power supply sys-

tems optimization model. Transportation Research

Part C: Emerging Technologies, 30(0):23 – 40.

Adeli, H. (2003). Expert Systems in Construction and Struc-

tural Engineering. Taylor & Francis.

Brunner, D., Cross, G., McGhee, C., Levis, J., and Whit-

ney, D. (1998). Toward increased use of simulation

in transportation. In Simulation Conference Proceed-

ings, 1998. Winter, volume 2, pages 1169–1175 vol.2.

BS-EN-15273 (2009). Railway applications. gauges. Tech-

nical report, -.

BS-EN-50119 (2009). Fixed installations. electric traction

overhead contact lines. Technical report, -.

Carretero, J., Perez, J. M., Garcia-Carballeira, F., Calderon,

A., Fernandez, J., Garcia, J. D., Lozano, A., Car-

dona, L., Cotaina, N., and Prete, P. (2003). Applying

rcm in large scale systems: a case study with railway

networks. Reliability Engineering & System Safety,

82(3):257 – 273.

ETI (2008). C(2008) 807-subsistema de energ´ıa del sistema

ferroviario transeuropeo de av. Technical report, -.

Gomez, C., Saa, R., Garcia, A., Garcia-Carballeira, F.,

and Carretero, J. (2012). A model to obtain optimal

designs of railway overhead knuckle junctions using

simulation. Simulation Modelling Practice and The-

ory, 26(0):16 – 31.

Goodman, C., Siu, L. K., and Ho, T. (1998). A review of

simulation models for railway systems. In Develop-

ments in Mass Transit Systems, 1998. International

Conference on (Conf. Publ. No. 453), pages 80–85.

Hani, Y., Chehade, H., Amodeo, L., and Yalaoui, F. (2006).

Simulation based optimization of a train maintenance

facility model using genetic algorithms. In Service

Systems and Service Management, 2006 International

Conference on, volume 1, pages 513–518.

Kiessling, F., Puschmann, R., and Schmieder, A. (2009).

Contact lines for electric railways: planning, design,

implementation. Publicis.

Kitchin, F. and Holland, J. (1950). Railway electriﬁcation:

design of overhead equipment. Electrical Engineers,

Journal of the Institution of, 1950(11):292.

Naweed, A., Hockey, G., and Clarke, S. (2013). Design-

ing simulator tools for rail research: The case study

of a train driving microworld. Applied Ergonomics,

44(3):445 – 454.

Nejlaoui, M., Houidi, A., Afﬁ, Z., and Romdhane, L.

(2013). Multiobjective robust design optimization of

rail vehicle moving in short radius curved tracks based

on the safety and comfort criteria. Simulation Mod-

elling Practice and Theory, 30(0):21 – 34.

Saa, R., Garcia, A., Gomez, C., Carretero, J., and Garcia-

Carballeira, F. (2012). An ontology-driven deci-

sion support system for high-performance and cost-

optimized design of complex railway portal frames.

Expert Systems with Applications, 39(10):8784 –

8792.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications