Numerical Backward Simulation Model

with Case Branching Capability

Yukio Hiranaka, Houjin Sakaki, Kenta Ito, Toshihiro Taketa and Shinichi Miura

Department of Informatics, Yamagata University, Yonezawa, Japan

Keywords: Backward Simulation, Numerical Backward Model, Case Branching Simulation, Range Signal.

Abstract: The authors are studying backward simulators which trace from results to causes for comprehensive

verification of system safety. It is not easy to make a backward simulation model because the forward

model may not be expressed in a reversible formula, or it is not reversible in cases of multiple inputs or

inclusion of internal state variables. In this paper, we propose a backward simulator which can incorporate

numerical simulation models and has a case branching capability to deal with multiple inputs. As a practical

simulation target, we implemented a simulator for testing stability of dynamic pricing for power usage

control as a smart grid application. We show some illustrating results of the backward simulation.

1 INTRODUCTION

Securing proper operation of software systems is a

great concern for our IT centric society. Software

engineers are doing their elaborate work to achieve

safety of their system by tests, which cannot be fully

done for almost all the applications. Essential

difficulty in the work comes from the fact that

engineers start their design by a forward thinking for

implementing functions to accomplish the objective

of the system, and they will take in unexpected

situations in their system, unintentionally.

A secure system might be designed by a backward

thinking to use only secure components with a safe

structure by considering all the unfavorable

conditions which may be encountered. However, it

may be a practical way that we design a system in a

forward thinking and check the safety of it by

backward testing. We describe a method for such

check with rounding up failure conditions by a

backward simulator in this paper.

2 BACKWARD SIMULATION

AND TARGET SIMULATION

We describe our backward simulator for a case of

control situation. As a smart power grid application,

dynamic pricing is planned and evaluated for

suppressing electricity consumption (Schweppe et al,

1981, Freeman, 2005,

Mohsenian-Rad 2010, Fan,

2011, Koulsopoulos and Tassiulas, 2011). The idea

is simple enough that consumers will reduce their

usage if the power company raise the price of

electricity. However, some may worry about the

dynamic behaviour of user and price determination.

If many consumers use some kind of automatic cost

cutter or economizing unit, power usage will be

decreased instantly after the price raised or

announced to be lowered and will be increased

instantly after the price lowered or announced to be

raised, and then, oscillation should be observed,

which might be uncontrollable at the worst.

We should investigate full consequences of the

system behaviors. Usually, it is not possible to test

all the conditions that the system would encounter

by using a forward simulator because the cases to be

tested would be huge in number.

There are backward approaches to search a

reasonable solution under certain restrictions such as

a dynamic allocation of resources (Huang et al.,

2009) and fault analysis (FTA). However, there is no

practical backward simulator for detecting

unfavorable conditions without leak.

So, we created a backward simulator to round up

all the unfavorable conditions by defining range

signals (Hiranaka et al., 2012). A range signal

expresses the range of values on control links and it

is used to calculate the possible input signal in the

backward simulation. If we start with unfavorable

output range, we can calculate input range signal

225

Hiranaka Y., Sakaki H., Ito K., Taketa T. and Miura S..

Numerical Backward Simulation Model with Case Branching Capability.

DOI: 10.5220/0005096302250230

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 225-230

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

which covers the condition on which the unfavorable

output occurs. Our aim is to detect such range, to

narrow down the condition and, then, to verify

whether the system would output unfavorable value.

Our backward simulator was implemented by

using Scala Language to use its Actor functions.

Range signals are expressed in XML style data

format (we call it as UCF Universal Communication

Format) which is comprised of the destination part

and the content part. The simulator has forward

simulation functions and distinguishes forward and

backward signal by the destination part of range

signals. If the destination is an input (typically

identified by <i>) of the block, then the content part

will be processed by the forward algorithm. If the

destination is an output (typically identified by <o>),

then the content part will be processed by the

backward algorithm.

It is not an easy task to make a backward

simulator, generally. The difficulties are encountered

to make a backward algorithm for each simulation

component when the forward algorithm is not

expressed in a simple formula, when it has multiple

inputs and when it has inner state variables which

cannot be determined from the output. Our solutions

to such situations are by using numerical inclusive

algorithm, by case branching (Hiranaka et al., 2013)

with dividing the possible conditions into finite

cases of input range pairs, and by externalizing the

inner state variables out of simulation blocks,

respectively. This paper shows the former two

methods.

Fig.1 is the whole view of a simple forward

simulation structure for testing dynamic pricing.

Four blocks represent a pricing block, a room

temperature sensor block, a user response block and

a heater block. The block named as sim is the

simulation controller which can intervene or

advance the simulation sequences by its

coordination function. All the simulation blocks

send their range signal messages to sim and sim

relays them to the predetermined block(s) down the

flow.

temp

user

heater

price

sim

Figure 1: Forward simulator example.

Fig.2 shows the backward simulation structure

corresponding to Fig.1, just reversed the direction of

signal flows indicated by dashed lines. The

component manin is a signal injection component

for initiating backward simulation. Along the

backward flow, the value range expressed by the

range signal will gradually become wider because

the backward algorithm needs to be designed to a

safer side, not to leak unfavourable conditions.

temp

user

heater

price

manin

sim

Figure 2: Backward simulator corresponding to Fig.1.

3 NUMERICAL FORWARD AND

BACKWARD MODEL

This section describes how the numerical model

blocks are formed. As for a case of electric oil heater

(De’Longhi TDD0915W), we measured switch

position to power usage relation, which is

summarized in Table 1. Then, the forward algorithm

of heater is to output power usage corresponding to

the input switch position (0 to 3). The backward

algorithm is to output the range of switch position

corresponding to the power usage range, e.g. range 1

to 2 switch position in response to 0.5 kW to 1 kW

backward signal. If the incoming power usage range

does not cover any of the values, this component

sends an out of range message to the simulation

controller.

An example of backward range signal from heater

component to user component is

<user><s>delong<s>i</s></s><t>100.0</t><o>1,

2</o><user>

where <s> tag means message source with nested

source i, which means the input port of delong

heater, and <o> tag means the entry point of the

range data “1,2.” The tag <t> means timestamp

indicating output time relative to the forward

simulation start time. It is advanced in forward

simulation and rewound in backward simulation for

the specified value predetermined by each

simulation component.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

226

Table 1: Characteristics of De’Longhi heater.

Switch position power usage(kw)

0 0.0

1 0.58

2 0.83

3 1.39

Forward pricing model was set as in Table 2,

where p is the price (Yen/kWh), u is the total usage

(kW) and C is the supply capacity (kW). It may be

determined by a mathematical formula (such as in

Fan, 2011). Backward model for the price

component (Table 3) is just an exchange of input

and output of Table 2, from which the range of

power usage divided by the capacity is determined

by price value or by range of price values.

Forward user model was set as in Table 4,

representing a user who determines the switch

position of the heater responding to the electricity

price and the selected room temperature. Backward

model for the user component (Table 5) is derived

from Table 4, from which range of room

temperature is determined by the switch position

depending on the electricity price. In this case, we

need to select which price value to be simulated

further. Such selection and proceeding is dealt by

case branching described latter.

Table 2: Forward price model.

u/C P (Yen/kWh)

low high

0 0.5 11

0.5 0.8 22

0.8

∞

Table 3: Backward price model.

p (Yen/kWh)

u/C

min max

11 0 0.5

22 0.5 0.8

44 0.8

∞

Table 4: A forward user response model.

room

temperature

p (Yen/kwh)

11 22 44

0 3 3 3

5 3 3 3

10 3 3 2

15 3 2 1

20 2 1 0

25 0 0 0

Table 5: Backward user response model corresponding to

Table 4.

Switch

position

room temperature range

price=11 price=22 price=44

22.5 – ∞ 22.5 – ∞ 17.5 – ∞

1 22.5 – 22.5 17.5 – 22.5 12.5 – 17.5

2 17.5 – 22.5 12.5 – 17.5 7.5 – 12.5

- ∞– 17.5 - ∞ – 12.5 - ∞ – 7.5

The forward temp component is just send the

current room temperature to the user block. We set it

as constant for the simulation period. Backward

temp model has a special function. It can accept any

valid room temperature range, but it assumes that the

temperature is constant for the simulation period and

do not allow the incoming temperature range to be

outside of the former range, then, gradually

narrowed by successive backward temperature range

signal. If it detects invalid temperature range, it

informs sim that the current case corresponding to

the invalid range signal is not feasible.

4 RANGE VS. RESOLUTION

As stated in the section 2 referring to Fig.2, value

range of range signals are getting wider through the

backward simulation and would spread too much.

However, we can get detailed results by dividing the

range.

Fig. 3 shows how the division of range signal

affects the simulation resolution, which means the

degree of coincidence between the resultant range

and the true area of unfavorable conditions. In the

figure, (a) shows the true area of unfavorable

conditions, (b) shows the rectangle which is defined

by the range of x and the range of y, (c) shows a

narrowed area defined by a combination of

rectangles for each divided range of x and range of

y. And if we proceed the range division further as in

(d), we will come closer to the true area of question.

Such improvement of resolution can be done by

dividing the temperature range in the user model.

5 CASE BRANCHING CONTROL

In this section, we describe the details of case branch

processing. All the components in the Fig. 2 except

manin deals branch related messages of branch,

clearCase, nextCase, branchCompleted, which are

control messages between simulation components.

A component which needs to branch pushes the

cases to be tested further onto its case stack and

sends a branch signal with a unique branch id to sim.

NumericalBackwardSimulationModelwithCaseBranchingCapability

227

（ａ）

（ｂ）

（ｃ）

（ｄ）

Figure 3: Range signal division and result resolution.

In the response to it, sim sends a branch signal and a

clearCase signal in sequence, each with the branch

id, to all the components.

Receiving the branch signal, every component

prepares to branch by storing the internal states and

keeps branch id in its local branch id stack.

Receiving the clearCase signal, it resets the internal

state to be the saved status, and sends a ready signal

to sim. Receiving ready signals from all the

components, sim sends a nextCase signal to all the

components. Receiving the nextCase signal, only the

component which generated the branch id coinciding

with the branch id in the nextCase message pops up

a case from its case stack and sends the related range

signal for the selected case backward to the

connected upstream component through sim. Then

sim proceeds simulation for the case selected by the

branch generated component.

If any of the components detects invalid incoming

range signal, it will send nextCase message to sim.

Receiving nextCase message, sim sends a clearCase

message to all the components and return to the state

of waiting ready signals from all the components

before to proceed to the next nextCase. If all the

cases for one branch have been tested, the

component which generated the branch sends a

branchCompleted message to sim with branch id,

and sim sends the branchCompleted message to all

the components. Receiving branchCompleted

message, all the components including sim pop the

branch id stack and prepares to proceed the former

simulation before that branch.

An example of branch message from user to sim

where “user#1” is the branch id generated by the

user component. Other messages like clearCase,

nextCase, breanchComplete and ready use the same

format by changing the <branch> tag to a tag of each

message’s name.

D X

sim

Figure 4: Invalid signal to stop processing the case.

6 IMPLEMENTATION AND

RESULTS OF OPERATION

Fig. 5 shows GUI windows of simulation

components. Fig.6 shows an example of command

window display. The simulation controller sim has a

step button for stepwise checking. And also, it has a

nextCase button for manually skip the current case

to the next case because we have no algorithm to

stop a branched case which may run forever.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

228

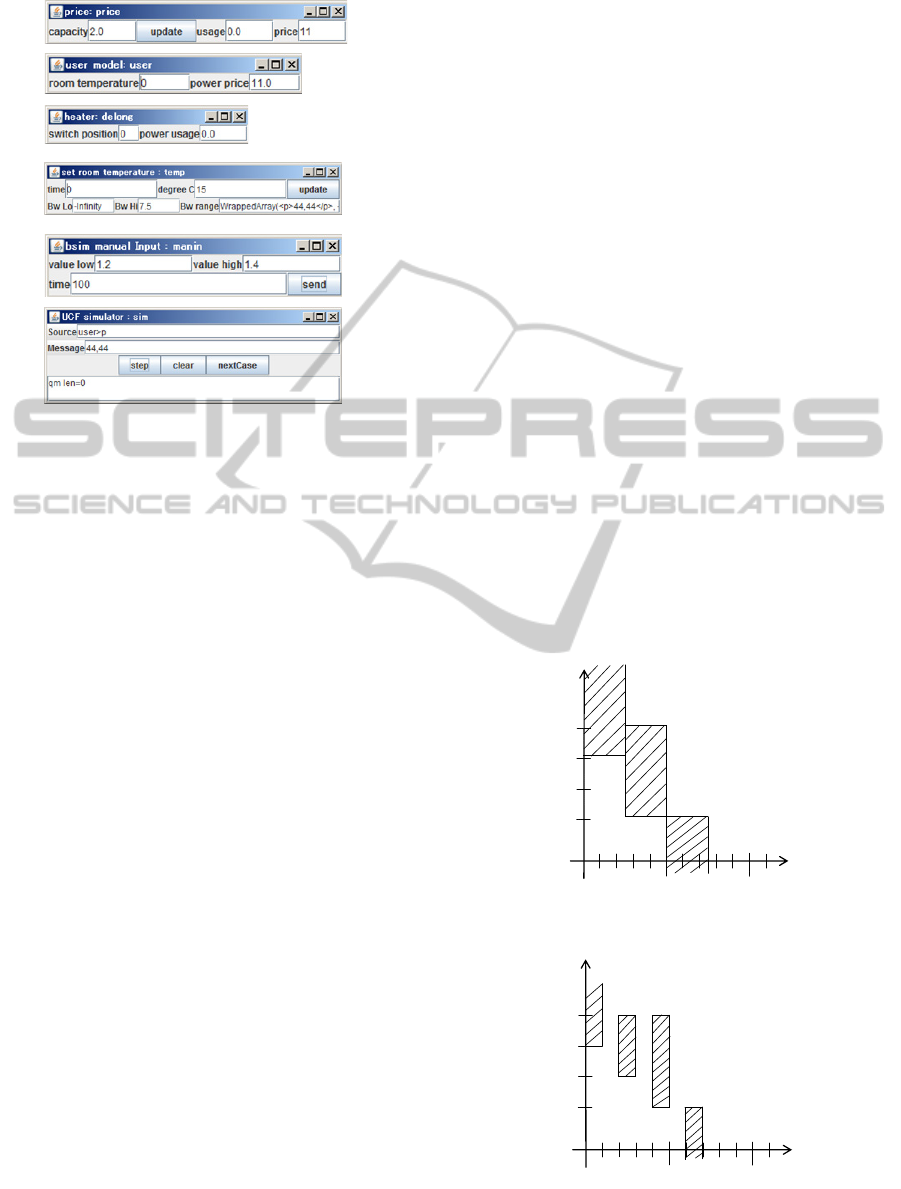
Figure 5: GUI for each simulation component.

$ scala P.P

Iprice started. capacity=2.0

Iuser started. room temperature=0 power price=11.0 Yen/kwh

Idelong started. switch positon=0

Itemp started. time=0 value=15

Imanin started. time=100 low=1.1 high=2.2

Isim started.

Btemp 0 15

Duser 0.0 3

Ddelong 1.0 1.39

Dprice 2.0 22

Duser 7.0 2

Ddelong 8.0 0.83

Dprice 9.0 11

Duser 14.0 3

Ddelong 15.0 1.39

Dprice 16.0 22

Figure 6: Console example of forward simulation.

Fig.7 shows a console display of a backward

simulation. The starting power usage value is

injected manually by using manin component. The

left end shows the type of console message and the

source of the message. At the center, time of

message generation is displayed and it goes

backward. The remaining message shows the range

values and supplemental information.

By injecting a range signal of power usage, e.g.

0 to 0.5kW, backward into the simulator, we can

determine whether the injected range is feasible or

not. If some component detects that incoming range

is not allowed, any value in the injected range

cannot be reached by the system. If the simulation

continues without such detection, it shows that there

is a condition which causes the system to output the

value inside the injected range. In such cases, we can

obtain temperature range for the injected range

because temp component of our implementation

keeps temperature range narrowed by successive

backward range signals.

Fig. 8 shows temperature range in relation to

injected power usage range of 0-0.5, 0.5-1.0, 1.0-1.5

or 1.5-2.0, each with 0.5kW interval. The hatched

area means the area of possibility. Fig.9 shows the

same relation in the case of 0.2kW interval. The

hatched area in Fig.9 is within that of Fig.8. It

indicates that we can arbitrary control the resolution

of the result.

Iprice started. capacity=2.0

Iuser started. room temperature=0 power price=11.0 Yen/kwh

Idelong started. switch positon=0

Itemp started. time=0 value=15

Imanin started. time=100 low=1.1 high=2.2

Isim started.

Bmanin 100 1.4,1.6

Wdelong 99.0 input 1.4, 1.6 is out of range 0.0, 1.39

Isim simulation completed.

Bmanin 100 1.2,1.4

Bdelong 99.0 input 3,3 for 1.2,1.4

Buser 94.0 input price=44,44 temp=-Infinity,7.5

Bdelong 92.0 input 2,3 for 0.8,Infinity

Buser 87.0 input price=44,44 temp=-Infinity,12.5

Bdelong 85.0 input 2,3 for 0.8,Infinity

Figure 7: Console example of backward simulation.

1.0

2.0

temp

22.5

17.5

12.5

7.5

Figure 8: Simulation result for 0.5kW step ranges.

1.0

2.0

temp

22.5

17.5

12.5

7.5

Figure 9: Simulation result for 0.2kW step ranges.

NumericalBackwardSimulationModelwithCaseBranchingCapability

229

Although the above results are for a simple

simulation model, it was shown that the backward

simulator can catch the unfavorable conditions and

can narrow down the area of such conditions.

To make Figs 8 and 9, we need to judge the

simulation trace displayed in Fig.7 whether it

continues forever or not for the feasible cases.

Probably, we have to set some time limit for each

case’s calculation, beyond which the simulator

automatically judges the case feasible.

7 CONCLUSION AND FUTURE

WORK

We designed the forward and backward simulator

with capability of using numerical simulation

models, backward range processing and case

branching. The implemented simulator shows

validity of the backward simulation for a simple case

of dynamic pricing control model planned for smart

grid.

We need to have many experiences by applying

the simulator to practical applications. Multiple user

simulation (Fig.10) is the top on our list, which

requires multiple branching components and a

backward sum component. We have to estimate

processing time of our backward simulator in the

case of large number of branches. Also, we plan to

design automatic judging algorithm for cases of

continuing or vibrating simulation. And also,

externalization of internal state variables will be

demanded in a complex system simulation.

temp

user１

heater1

price

user2

heater2

con-p

con-t

Figure 10: A backward simulation structure for two users.

ACKNOWLEDGEMENTS

This work was partly supported by JSPS KAKENHI

Grant Number 25540006. The authors wish to thank

the reviewers for their valuable comments.

REFERENCES

Chen, L., Steven, N.L., Low, H. and Doyle, J., 2010. Two

Market Models for Demand Response in Power

Networks, Proc. IEEE Int’l Conf Smart Grid Comm.

Fan, Z. 2011. Distributed Demand Response and User

Adaptation in Smart Grid, Proc. Integrated Network

Management, pp.726-729.

Freeman, R., 2005. Managing Energy: Reducing Peak

Load and Managing Risk with Demand Response and

Demand Side Management, Refocus, vol.6, no.5,

pp.53-55.

FTA, Fault Tree Analysis, http://en.wikipedia.org/

wiki/Fault_tree_analysis

Hiranaka, Y. and Taketa, T., 2012. Designing Backward

Range Simulator For System Diagnoses, Proc. XX

Imeko World Congress Metrology for Green Growth.

Hiranaka, Y., Taketa, T. and Miura, S., 2013. Case

Branching Backward Simulator for Integer

Factorization, Proc. 8th EUROSIM Congress on

Modeling and Simulation, pp.259-264.

Huang, C.C. and Wang, H.H., 2009. Backward Simulation

with Multiple Objectives Control, Proc. IMECS

(International MultiConference of Engineers and

Computer Scientist).

Koulsopoulos I. and Tassiulas, 2011. L., Challenges in

Demand Load Control for the Smart Grid, IEEE

Network, vol.25,no.5, pp.16-21.

Mohsenian-Rad, A.H., Wong V.W.S., Jatskevich, J.,

Schober, R. and Leon-Garcia A., 2010. Autonomus

Demand-Side Management Based on Game-Theoretic

Energy Consumption Scheduling for the Future Smart

Grid, IEEE trans. Smart Grid, vol.1, no.3, pp.320-331.

Schweppe F.C., Tabors R.D. and Kirtley J.L., 1981.

Homeostatic Control: The Utility/Customer

Marketplace for Electric Power, MIT Energy

Laboratory Report, MIT-EL 81-033.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

230