Propagating Model Refactorings to Graph Transformation Rules

Sabine Winetzhammer and Bernhard Westfechtel

Chair of Applied Computer Science 1 - Software Engineering,

University of Bayreuth, Universit

atsstraße 30, 95440 Bayreuth, Germany

Keywords:

Refactoring, Graph Transformation Rules, ModGraph.

Abstract:

Model-driven software engineering reduces the effort of developing software by replacing low-level program-

ming with the construction of high-level executable models. Refactoring improves the structure of software

artifacts without changing external behavior. Originally, refactoring was developed for and applied to (object-

oriented) programs. In the context of model-driven software engineering, refactoring has to be applied to both

structural and behavioral models. In this paper, we present tool support for model refactoring in ModGraph,

a tool which employs Ecore class diagrams for structural modeling and graph transformation rules for be-

havioral modeling. In particular, we focus on the propagation of refactorings of the structural model into the

behavioral model.

1 INTRODUCTION

Model-driven software engineering reduces the effort

of developing software by replacing low-level pro-

gramming with the construction of high-level exe-

cutable models. To this end, both structural and be-

havioral models have to be developed. In the con-

text of object-oriented modeling, there seems to be

a general consensus to employ some variant of class

diagrams for structural modeling, e.g., EMF, MOF,

or UML class diagrams. In contrast, there is a wide

spectrum of languages for behavioral modeling which

are based on different computational paradigms (e.g.,

state machines, activity diagrams, or rule-based trans-

formation languages). In this paper, we will focus on

behavioral modeling with graph transformation rules:

Models are considered as graphs, and transformations

of these graphs are speciﬁed declaratively by graph

transformation rules.

Software evolution is a discipline which provides

concepts, methods, and tools for evolving software in

response to changing requirements, platforms, tech-

nologies, etc. In the context of object-oriented soft-

ware development, evolution support is provided in

a variety of different ways, including e.g. design

patterns and refactorings, both of which facilitate

changes to the software. According to (Fowler, 1999),

refactoring denotes the activity of restructuring soft-

ware by applying a series of transformations without

affecting its externally observable behavior.

The transformations proposed in (Fowler, 1999)

were developed for and applied to (object-oriented)

programs. In the context of model-driven software en-

gineering, refactoring has to be applied to both struc-

tural and behavioral models. Previous work on model

refactoring focused on structural models (Biermann

et al., 2006; Mens, 2005; Mens et al., 2007). How-

ever, when the structural model is refactored, the re-

spective changes have to be propagated into the be-

havioral model; otherwise, the behavioral model is no

longer consistent with the structural model.

In this paper, we close the gap identiﬁed above,

resulting in comprehensive support for model refac-

toring. We present tool support for model refactoring

in ModGraph

, a tool which employs Ecore class dia-

grams for structural modeling and graph transforma-

tion rules for behavioral modeling. For the structural

model, ModGraph offers a set of refactoring trans-

formations along the lines of Fowler’s work (Fowler,

1999). The tool support goes beyond previous work

since the refactorings are propagated from the struc-

tural model into the behavioral model. Thus, graph

transformation rules are updated in response to the

changes of the underlying Ecore model.

Altogether, our work provides an important con-

tribution to model evolution, which is an essential pre-

requisite for putting model-driven software engineer-

ing to work. The term model evolution is used in a va-

riety of different contexts. Frequently, model evolu-

tion is concerned with the changes of model instances

http://btn1x4.inf.uni-bayreuth.de/modgraph/homepage

Winetzhammer S. and Westfechtel B..

Propagating Model Refactorings to Graph Transformation Rules.

DOI: 10.5220/0005098900170028

In Proceedings of the 9th International Conference on Software Paradigm Trends (ICSOFT-PT-2014), pages 17-28

ISBN: 978-989-758-037-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

a:EAttribute

C2: EClass

C1: EClass

RHS

LHS

a:EAttribute

C2: EClass

C1: EClass

a:EAttribute

C2: EClass

C1: EClass

Figure 1: A graph transformation rule shown as divided view and merged view.

in response to changes of the underlying metamodel

(Rose et al., 2010) (analogously to schema evolution

in databases (Banerjee et al., 1987)). In contrast, the

work presented in this paper has a different focus: It

deals with the consistent refactoring of a set of in-

terdependent models, which requires propagation of

the changes of the structural model into the behav-

ioral model. The migration of model instances is not

considered here.

The rest of this paper is structured as follows: Sec-

tion 2 explains the context in which this work was

performed. Section 3 provides an overview of our ap-

proach to refactoring both structural and behavioral

models. Section 4 describes the implementation. Sec-

tion 5 illustrates this approach by several examples.

Section 6 discusses related work. Section 7 concludes

the paper.

2 BACKGROUND

The work reported in this paper was carried out in

the context of the ModGraph project (Winetzhammer,

2012). ModGraph is a tool for model-driven soft-

ware engineering which is based on the Eclipse Mod-

eling Framework (EMF, see (Steinberg et al., 2009)).

Structural modeling is performed with Ecore. Thus,

a structural model consists of a set of classes owning

structural and behavioral features. Structural features

are partitioned into attributes, which have (collections

of) simple values, and references to target classes. By

default, references are uni-directional (from instances

of the source class to instances of the target class);

however, a pair of uni-directional references may be

grouped into a bi-directional reference. Behavioral

features are modeled by operations.

The structural model merely describes the signa-

ture of operations, but not their behavior. In Mod-

Graph, the behavior of an operation may be speciﬁed

declaratively by a graph transformation rule. Model

instances are considered as graphs whose nodes and

edges correspond to objects and links, respectively.

A graph transformation rule describes an in-place

model transformation and essentially consists of a

left-hand side and a right-hand side, like the one

shown on the left-hand side of Figure 1 to move an

attribute from one class to another. The left-hand side

describes the subgraph to be searched (the match for

the rule). Here the classes and the attribute that should

be moved are located. The right-hand side speci-

ﬁes the subgraph which replaces the left-hand side.

In case of Figure 1 the attribute references the other

class. The left-hand side and the right-hand side may

be merged into a single diagram, as shown in Figure

1 on the right-hand side. Elements belonging only to

one side need to be marked: only left-hand side ele-

ments are colored red and marked --, only right-hand

side elements are colored green and marked ++.

ModGraph uses the merged view. An example is

given in Figure 4. In ModGraph single and double

boxes represent single objects and sets of objects, re-

spectively. The current object on which the operation

implemented by the graph transformation rule is in-

voked is designated by the inscription this. Arrows

represent links, i.e., instances of references. Con-

ditions on and modiﬁcations of attribute values are

shown in the Constraints and Changes compartments

of the boxes for objects. Nodes designated as optional

are not required for the rule to match. According to

the merged view, insertions and deletions of objects

and links are represented by coloring the respective

graphical elements in green and red, respectively, as

well as markers ++ and -- are placed inside the boxes

for objects and near to the arrows for links. The mean-

ing of the graph transformation rule shown in Figure 4

will be described later.

Altogether, the ModGraph tool has to deal with

different types of models, as illustrated in Figure 2.

The blue boxes represent the models which are cre-

ated by the ModGraph user: The structural model

is deﬁned by an Ecore class diagram. The behav-

ioral model consists of a set of graph transformation

rules specifying the behavior of operations introduced

in the structural model. At runtime, graph transfor-

mation rules will be applied to model instances by

matching and replacing subgraphs. Internally, a graph

transformation rule is represented as a model, too

(namely an instance of the graph transformation meta-

model, which in turn is an instance of the Ecore meta-

model).

ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends

Ecore

Metamodel

GraphTransformation

Metamodel

Instance

Ecore

Model

instanceof

GraphTransformation

Rule

instanceof

update

instanceof

references

matches/transforms

Figure 2: The problem statement.

According to (Fowler, 1999), refactoring denotes

the activity of restructuring software by applying a

series of transformations without affecting its exter-

nally observable behavior. Fowler’s book contains

a bunch of refactoring transformations, all of which

refer to the source code. For each refactoring, the

following information is supplied: the precondition

under which the refactoring may be applied, the el-

ementary steps of the core refactoring, the impact

of changes on dependent model elements, and the

postconditions which hold after the refactoring. The

refactoring transformations vary in their complexity

and range from simple ones such as renaming an at-

tribute to complex refactorings such as pulling up an

attribute from all subclasses to a common superclass

and extracting a class from a given class by moving a

part of its features to the extracted class.

In this paper, we discuss refactorings of models

rather than refactoring of source code. More speciﬁ-

cally, we focus on models created by ModGraph users

(blue boxes in Figure 2). Thus, we consider the

following problem: Let us assume that a consistent

model is given, being composed of a class diagram

and a set of graph transformation rules. The graph

transformation rules are typed with the elements of

the structural model. ModGraph ensures that typing

is consistent: The class of an object must be deﬁned in

the class diagram, the attributes occurring in the ob-

ject’s compartments must be owned by that class, etc.

Now, the ModGraph user would like to apply a refac-

toring transformation to the overall model. To this

end, the structural model has to be changed and the

changes must be propagated into the graph transfor-

mation rules such that consistency is re-established.

3 PRELIMINARY

CONSIDERATIONS

As the last section described EMF and ModGraph

graph transformation rules as well as their inter-

play, this one focuses on problems concerning the

graph transformation rules co-occurring within refac-

toring the EMF model. Figure 2 shows the meta-

relationships between the models (blue, rounded ar-

rows), as well as the interplay between EMF and

ModGraph (black, bold arrows). ModGraph is deeply

rooted in the EMF world, taking a look at the meta-

relationships between the models. Each graph trans-

formation rule (Figure 2, blue box on the right) is an

instance of the graph transformation meta model (or-

ange box on the right) which was built with EMF us-

ing the Ecore metamodel (green box on the left). This

metamodel also serves as metamodel for Ecore class

diagrams (blue box on the left) . Those class diagrams

may be instantiated (black box on the left).

The graph transformation rule interacts with the

model and the instance. The ﬁrst interaction is caused

by the fact that each graph transformation rule imple-

ments an operation in the Ecore class diagram. There-

fore it references this operation as well as its con-

taining class. The second interaction takes place in-

side the rule: A ModGraph rule changes instances of

the Ecore model by matching structures and applying

changes. The components inside the rule reference el-

ements of the structural model, e.g. an object in a rule

must reference an EClass inside the Ecore model, a

link has to reference an EReference.

These two dependencies are shown as black, bold

arrows named ”references” and ”matches / trans-

forms” in Figure 2. A full overview of the dependen-

PropagatingModelRefactoringstoGraphTransformationRules

Meta‐Rule /

Xcore Operation

Instance

Ecore

Model

GraphTransformation

Rule

references

matches/transforms

Transformation(Rule)

Perform a

refactoring!

Interdependent

set of models

refactor refactor

call

refactoring

propagate

changes

Figure 3: Interaction of the refactoring engine with the affected models.

cies between a rule and the structual model is given

in (Buchmann et al., 2012) with an explanation of the

ModGraph metamodel for graph transformation rules.

Within a static context, this kind of model exe-

cution will probably never cause any problems. But

many models evolve in time: elements are renamed,

references are re-targeted and classes are inlined or

extracted in order to create or collapse inheritance hi-

erarchies or just to improve the model - in short: the

model is refactored. Regarding only Ecore models,

applying these refactorings is well understood and im-

plemented in several ways, as we will show in Sec-

tion 6. The problem is caused by the strong intercon-

nection between a rule and the Ecore model. If any

element is just referencing the refactored model ele-

ment, after refactoring, this reference is unset. Hence,

the rule is invalid because of inconsistencies between

the rule and the model, which will be eliminated by

our approach. We propose to propagate refactorings

to rules, with the help of rules, as shown in Figure 3.

We use two steps: First we call the modeled refac-

toring rules, second we propagate the refactorings

performed by these rules to the graph transformation

rules belonging to the refactored static model by using

mostly meta-rules. That way we provide refactoring

on graph transformation rules executed by other graph

transformation rules, we call meta-rules.

Our approach starts with Fowler’s deﬁnition of

each refactoring. As these deﬁnitions were introduced

for the refactoring of (object oriented) code, we adapt

the deﬁnitions for Ecore model refactorings. Subse-

quently we investigate how the changes affect Mod-

Graph rules. Here we consider different aspects con-

cerning the structure of the rule. Depending on the el-

ement the changes may cause minor or major changes

to be performed inside the rule. Table 1 shows some.

One may classify the affected rule elements as shown

in the ﬁrst column: the whole rule, nodes (repre-

senting single- and multi-valued objects and param-

eters), attributes, links (instances of references), and

textual conditions (e.g. pre- and postconditions, at-

tribute conditions), as well as ﬁelds (e.g. operation

calls). The result of this step is taken to propagate

the changes to the rules. The change may be a simple

setter call on the graph transformation rule or restruc-

turing of the rule itself, as Section 5 will show.

The rule as a whole references an operation and its

containing class. Hence changes performed here need

to be propagated. A rule is superseded if the operation

is deleted. If the class is deleted, the rule may be as-

signed to another class where a similar operation shall

take place now or is also deleted. A node references

a class. It needs to be updated whenever the class

changes. If for example the class is renamed, the node

needs to be retyped. If the class is made abstract, the

node will be deleted if its status is CREATE. For any

other status it will be retyped. Attributes are an essen-

tial part of a rule. They may be used to add conditions

to nodes as well as for assignments. Each attribute in a

rule references an attribute in the Ecore model. There-

fore an attribute in a rule needs to follow the attribute

in the class. Renaming and moving may be executed

without problems, but retyping is quite interesting: If

an attribute is retyped in the Ecore model and used

inside a graph transformation rule the user has to as-

sign its new value manually. Furthermore attributes

may be moved and links be re-targeted. In both cases

the refactoring tries to locate an instance of the new

container / target of the attribute / link and to move /

re-target the attribute / link, respectively. If this fails

the attribute / link is deleted. For the textual parts of

the rules exists no other way than parsing them to ﬁnd

the elements referred and to adapt them using naming

conventions.

ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends

Table 1: Effects of model changes on different classes of rule elements.

Affected rule element Change in Ecore model Change modeled in meta-rule

Class

rename adapt references to class

delete adapt references to class, if not successful: delete

Whole rule make abstract adapt references to class

Operation

rename adapt references to operation

delete delete

Class

Nodes rename retype

delete delete

make abstract retype or delete

Attribute in Class

rename adapt name

Attributes move try to move, if not successful: delete

retype retype and assign new value

delete delete

Reference

Links rename adapt name

retarget try to retarget, if not successful: delete

delete delete

Textual conditions, any change parse condition and propagate re-

paths and ﬁelds factoring, if refactored element is found

4 IMPLEMENTATION

The refactoring is implemented using ModGraph/X-

core

and Java to implement connectors using exten-

sion points. For the static structure, we mainly use

two classes in an Xcore model: Refactoring, to specify

the refactorings on the model (as started in (D

ummel,

2013)), and Propagation, to propagate the changes

caused by them.

As we want to use the added value of rules only,

each refactoring on the model is speciﬁed inside a

graph transformation rule or an Xcore operation, de-

pending on its complexity. We will see in detail in

Section 5, that the change of a bi- to a unidirectional

reference is modeled very well with rules, while re-

naming an element in the model can be written easily

in a few lines inside an Xcore operation. Please note,

that these refactorings are universal. They also work

for Ecore models outside the ModGraph context.

The propagation of changes to ModGraph rules

follows the same scheme. A complex propagation is

modeled as a rule, using Xcore as control ﬂow lan-

guage, if necessary. A simple propagation is modeled

The approach to use ModGraph and Xcore is described

in (Winetzhammer and Westfechtel, 2013) and (Winet-

zhammer and Westfechtel, 2014).

as an Xcore operation. In Section 5, examples for

propagations are shown.

As a ﬁnal step of propagation, all rules changed

are validated in order to secure their navigability.

Navigability means, that each single- or multi-valued

object needs to be reachable by navigating links start-

ing from the current object or a single- or multi-

valued parameter of the operation. If the validation

fails the user needs to adjust the rule manually. That

way, rules which are no more navigable after apply-

ing the refactoring will be marked for further manual

changes.

The rest is implemented in Java: We extend a

popup-menu in order to be able to call the refactoring

in the model and call the refactoring rule implementa-

tion (written in ModGraph/Xcore). After successfully

executing this one, we call the propagation implemen-

tation (written in ModGraph/Xcore), that propagates

the changes to the rules. The propagation locates the

rules, parses and ﬁxes them as shown in the next para-

graph. The result is a complete model evolution.

We implemented the following refactorings and

their propagations. A validation of the rules is per-

formed after each refactoring.

Rename Element: Renames an ENamedElement.

Propagates the new name to the corresponding el-

PropagatingModelRefactoringstoGraphTransformationRules

ements in the rules. (See Section 5)

Add Parameter: Adds an EParameter to an EOp-

eration. Propagate to implemented operation and

textual ﬁelds, especially to operation calls, in a

rule. Both need to be adapted.

Remove Parameter: Removes an EParameter from

an EOperation. Propagation: Removes the param-

eter from the rules, updates textual ﬁelds, espe-

cially operation calls.

Change Value to Reference: Updates the contain-

ment hierarchy. Propagation: Validate rules in or-

der to check exclusiveness.

Change Reference to Value: Updates the contain-

ment hierarchy. No propagation.

Change Bi- to Unidirectional Reference: Re-

moves an EReference. Propagation: Exchanges

each link targeting the deleted reference by a link

targeting its former opposite reference. (See Sec-

tion 5)

Change Uni- to Bidirectional Reference: Adds an

EReference and sets its EOpposite. No propaga-

tion.

Extract Class: Extracts an EClass from a given

EClass and relates them using an EReference.

Propagation: If a node references the given class,

check if it uses attributes, operations or references

moved to the extracted class. If yes, create a

new node referencing the extracted class and re-

late both using a link which is an instance of the

EReference relating the classes. Move the ele-

ments referencing the extracted class to the newly

created node.

Extract Subclass: Extracts a subclass from a given

class. Propagation: If operations, attributes or

references are moved, retype the nodes referenc-

ing the class and using one of the operations, at-

tributes or references to be typed over the sub-

class.

Extract Superclass: Extracts a superclass from a

given class. No propagation, because of inheri-

tance.

Inline Class: Inlines a class into another class.

Propagation: Retype all nodes typed over the in-

lined class to the class in which it will be inlined.

Move Attribute / Operation: Moves the attribute /

operation from a source to a target class. Propa-

gation: If the rule contains two nodes referencing

the source and target class move the usage of the

attribute / operation. In all other cases delete the

usage.

Pull Up Attribute / Operation: Moves the attribute

/ operation to the super class. No propagation, be-

cause of inheritance.

Push Down Attribute / Operation: Moves the at-

tribute / operation to the subclasses. Propagation:

If there is a node typed over the super class us-

ing the pulled down attribute / operation, ask user

to which subclass it shall be retyped and perform

this.

Replace Subclasses with Fields: Creates an enu-

meration with one literal for each subclass and

an attribute typed over the enum in the super-

class. Propagation: Replace the nodes typed over

the subclasses by nodes typed over the superclass

with the corresponding literal assigned.

Hide Delegate: Removes the direct EReference be-

tween two EClasses. Propagation: Delete corre-

sponding links in rules.

Remove Middleman: Creates a direct EReference

between two EClasses. Propagation: Create the

corresponding link, if the rule contains two nodes

referencing the classes.

Replace Inheritance with Delegation: Replace the

existing generalization with an EReference. Prop-

agation: If both classes are referenced by nodes

inside a rule create a link referencing the ERefer-

ence.

Replace Delegation with Inheritance: Replace an

existing EReference with a generalization. Prop-

agation: Remove the link referencing the ERefer-

ence.

5 EXAMPLES

The general idea of propagating model refactorings

on interdependent models is now concretely shown

considering the refactoring change a bi-directional to

a uni-directional reference in detail. The refactoring

to rename an element is sketched by the special case

of renaming a class.

5.1 Change a Bi- to a Uni-directional

Reference

The refactoring we consider here in detail is chang-

ing a bi- to a uni-directional reference. Starting with

Fowler’s deﬁnition (Fowler, 1999), we provide the

implementation of the model change as well as the

meta-rule to propagate the changes.

Fowler deﬁnes this refactoring as follows: ”You

have a two-way association but one class no longer

ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends

Figure 4: Rule for changing a bi- to a unidirectional reference in an Ecore class diagram.

Figure 5: Rule propgagating a change of a bi- to a unidirectional reference in an Ecore class diagram to graph transformation

rules. The numbers must be replaced by the corresponding OCL conditions shown in Listing 1.

needs features from the other.”(Fowler, 1999) For

EMF this means, that a reference with an opposite

set is deleted. The rule to perform the operation in

the Ecore model is shown in Figure 4. Here a refer-

ence called reference2 (red box, marked with --) is

deleted within all its links (red arrows, marked with

--) to classes as well as its opposite relation to the

other reference, called formerOpposite.

To propagate this refactoring, we use an Xcore

operation and two meta-rules. The meta-rule shown

in Figure 5 shows the application of the refactor-

ing propagation to links in the Graph Pattern. The

PropagatingModelRefactoringstoGraphTransformationRules

Figure 6: Graph transformation rule before and after in-

voking the refactoring change bi- to uni-directional refer-

ence on the model. toS and toP are instances of the equally

named references in the model, which are opposed.

meta-rule for the negative application conditions is

structured analogously and therefore not shown here.

These two meta-rules are applied to all rules belong-

ing to the refactored model using an Xcore imple-

mented operation. First, the operation loads the whole

rule, second it calls both meta-rules, third it updates

the diagram for the rules and ﬁnally it saves the mod-

iﬁed resource.

In the meta-rule the deleted reference is located.

Each link, called delLink in Figure 5, is referencing

the deleted reference and is therefore deleted. A new

link, called link in Figure 5, is created as an instance

of the former opposite of the deleted reference. The

numbers next to the paths in the rule represent OCL

path expressions, shown in Listing 1. They ensure

consistency for pattern matching. No. 1 and 2 en-

sure that the nodes node1 and node2 are referencing

the classes between which the refererences has been

deleted. No. 3 and 4 ensure that a link, referencing

the deleted reference exists in the rule.

The refactoring is applied to a test project. The

model contains a bidirectional reference modeled as

two EReferences called toS and toP, which are set as

EOpposite to each other. The project also contains a

set of graph transformation rules. One of the rules is

shown in the upper part of Figure 6, where an instance

of a parameter p shall be deleted. This instance is con-

nected using a link, an instance of the toP reference, to

the current object. Now let us assume that the user de-

cides toP is no more needed in the class diagram and

therefore calls our refactoring rule to change the bi- to

a uni-directional reference. toP is removed from the

structural model. Also our propagation mechanism

changes the rules. The result for our example rule is

shown on the lower part of Figure 6.

5.2 Rename Element

Renaming an element is a quite common task in pro-

gramming and modeling ever since. This is an inter-

esting example, as the refactoring for the structural

model can be written as a few lines in an Xcore op-

eration, but the changes to be propagated to the rules

are not as trivial: As this refactoring may affect all

components of an Ecore model, all components of

a rule referencing those may be concerned. Due to

the fact, that elements of a rule reference model el-

ements differently, there are a number of renaming

propagations. Starting with the simple part, Listing 2

shows the implementation for the refactoring of the

structural model. The renamed element as well as

its new name are given as a parameter to the opera-

tion. First our implementation checks if the element’s

container already contains any element with the given

new name. If not, the element is renamed.

The rather complex part is the propagation that is

decomposed into several meta-rules and Xcore opera-

tions. For the meta-rules we distinguish between each

element that is referred in the class diagram. Hence,

we need at least one rule or Xcore operation to prop-

agate the renaming of a class, an attribute, an opera-

tion, or a reference.

As an example we consider the propagation of re-

naming a class in the Ecore model. The ﬁrst step is to

rename the class in the model itself. This is performed

by a call for a setter. In the next step all graph trans-

formation rules are searched using the criteria shown

in Table 2 in the left column. If one of these ques-

tions is answered positively, the rule needs to be ad-

justed. Depending on which answers were positives,

the changes in the right column are applied to the rule

in order to get a consistent set of models. Assume

the answer to the ﬁrst question is yes. The next ques-

tion is also answered positively, if the rule contains

a current object. Figure 7 shows the meta-rule for

the propagation. The corresponding class of the rule

is set to the renamed one, the current object this is

retyped and possible unbound nodes referring to the

class are also retyped directly. Links as instances of

references typed over the renamed class are adapted

in an extra meta-rule, which is called by an operation

call in the current object of the meta-rule shown here.

The same holds for the operations resetImplemente-

dOperation and handleInnerNodes. The ﬁrst one cor-

rects the implemented operation’s path, the latter han-

dles attributes in unbound nodes. Textual elements

are handled separately. Please note that retyping by

renewing the type / corresponding class is necessary

here, as these are inter-model dependencies which are

lost by changing the corresponding object.

ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends

Listing 1: OCL path expressions for change bi- to unidirectional reference.

1 1 : [ ( s e l f . o c l IsT y p e O f ( GT T h is O bje c t ) and s e l f . o c l A sType ( GTTh i sOb j ec t)−>

2 e x i s t s ( e | e . t y p e . oc l A s T y p e ( e c o r e : : E C l a s s ) . name =

3 f o r m e r O p p o s i t e . e R e f e re n c e T y p e . o clAsType ( e c o r e : : E C l a s s ) . name ) )

4 o r ( s e l f . o c l I s T y p e O f ( GPUnboundNode ) and s e l f . oclAsTy p e ( GPUnboundNode)−>

5 e x i s t s ( e | e . t y p e . oc l A s T y p e ( e c o r e : : E C l a s s ) . name =

6 f o r m e r O p p o s i t e . e R e f e r e n c e T y p e . o clAsType ( e c o r e : : E C l a s s ) . name ) )

7 o r ( s e l f . o c l I s T y p e O f ( GPBoundNode ) and s e l f . oclAsT y p e ( GPBoundNode)−>

8 e x i s t s ( e | e . t y p e . oc l A s T y p e ( e c o r e : : E C l a s s ) . name =

9 f o r m e r O p p o s i t e . e R e f e re n c e T y p e . o clAsType ( e c o r e : : E C l a s s ) . name ) ) ]

11 2 : [ ( s e l f . o c l I s T y p e O f ( GT T h is O bje c t ) and s e l f . o c l A sType ( GTTh i sO b j ec t)−>

12 e x i s t s ( e | e . t y p e . ocl A s T y p e ( e c o r e : : E C l a s s ) . name =

13 f o r m e r O p p o s i t e . e C o n t a i n e r . oclAsTy p e ( e c o r e : : ECl a s s ) . name ) )

14 o r ( s e l f . o c l I s T y p e O f ( GPUnboundNode ) and s e l f . o c l A s T ype ( GPUnboundNode)−>

15 e x i s t s ( e | e . t y p e . ocl A s T y p e ( e c o r e : : E C l a s s ) . name =

16 f o r m e r O p p o s i t e . e C o n t a i n e r . oclAsTy p e ( e c o r e : : ECl a s s ) . name ) )

17 o r ( s e l f . o c l I s T y p e O f ( GPBoundNode ) and s e l f . o c l A s T ype ( GPBoundNode)−>

18 e x i s t s ( e | e . t y p e . ocl A s T y p e ( e c o r e : : E C l a s s ) . name =

19 f o r m e r O p p o s i t e . e C o n t a i n e r . oclAsTy p e ( e c o r e : : ECl a s s ) . name ) ) ]

21 3 : [ s e l f . e l e m e n t s −> s e l e c t ( n | n . o c l I s K i n d O f ( GTNode ) and n . oc l A s T y p e ( GTNode ) . o u tg oi n g E d g e s −>

22 e x i s t s ( e | e . o c l I s K i n d O f ( GPLink ) and e . o c l A sType ( GPLink ) . e x R e f e r e n c e . e I s P r o x y ( ) ) ) ]

24 4 : [ s e l f . e l e m e n t s −>s e l e c t ( n | n . o c l I s K i n d O f ( GTNode ) an d n . oclAs T y p e ( GTNode ) . in c o ming E d ges−>

25 e x i s t s ( e | e . o c l I s K i n d O f ( GPLink ) and e . o c l A sType ( GPLink ) . e x R e f e r e n c e . e I s P r o x y ( ) ) ) ]

Listing 2: Xcore implementation of refactoring rename element.

1 op vo i d renameENamedElement ( ENamedElement e l e m e n t , S t r i n g newName ) {

2 i f ( e l e m e n t . e C o n t a i n e r . e C o n t e n t s . f i l t e r ( e | e . e C l a s s == E Cl as s ) . e x i s t s [ e |

3 e . e C l a s s == e l e m e n t . e C l a s s && ( e as E C l a s s ) . name == newName ] ) {

4 re t u r n / ∗ and show message ∗ /

5 } e l s e {

6 e l e m e n t . name = newName

7 }

8 }

Table 2: Strategy for the rename element refactoring when renaming a class in the structural model.

Does the rule reference this class? Change the reference to the class

and retype the current object.

Does the rule contain nodes referencing this class? Retype the node.

Do those nodes contain inner nodes Retype them.

referencing contained elements of this class?

Does the rule contain links referencing Retype links.

EReferences typed over the class?

Does the rule contain textual elements making use of this class? Get the new name and replace the old one.

6 RELATED WORK

Mens (Mens and Tourw

e, 2004) provides a compre-

hensive survey of software refactoring. Fowler’s book

probably constitutes the most cited reference in this

domain (Fowler, 1999). The refactorings presented in

this book all apply to object-oriented programs, i.e.,

they are applied to source code rather than models.

Furthermore, refactorings are described in an infor-

mal way. A formalization which is based on program

graphs and graph transformation rules is presented

in (Mens et al., 2005). A major restriction of this

work consists in the fact that only individual rules are

considered. In the general case, programmed graph

transformation rules are required for specifying refac-

toring transformations. This is demonstrated e.g. by

(Geiger, 2008), in which a refactoring case prepared

for the GraBaTs 2008 workshop was realized in Fu-

jaba (Z

undorf, 2001). The refactoring case included

three refactorings on program graphs.

PropagatingModelRefactoringstoGraphTransformationRules

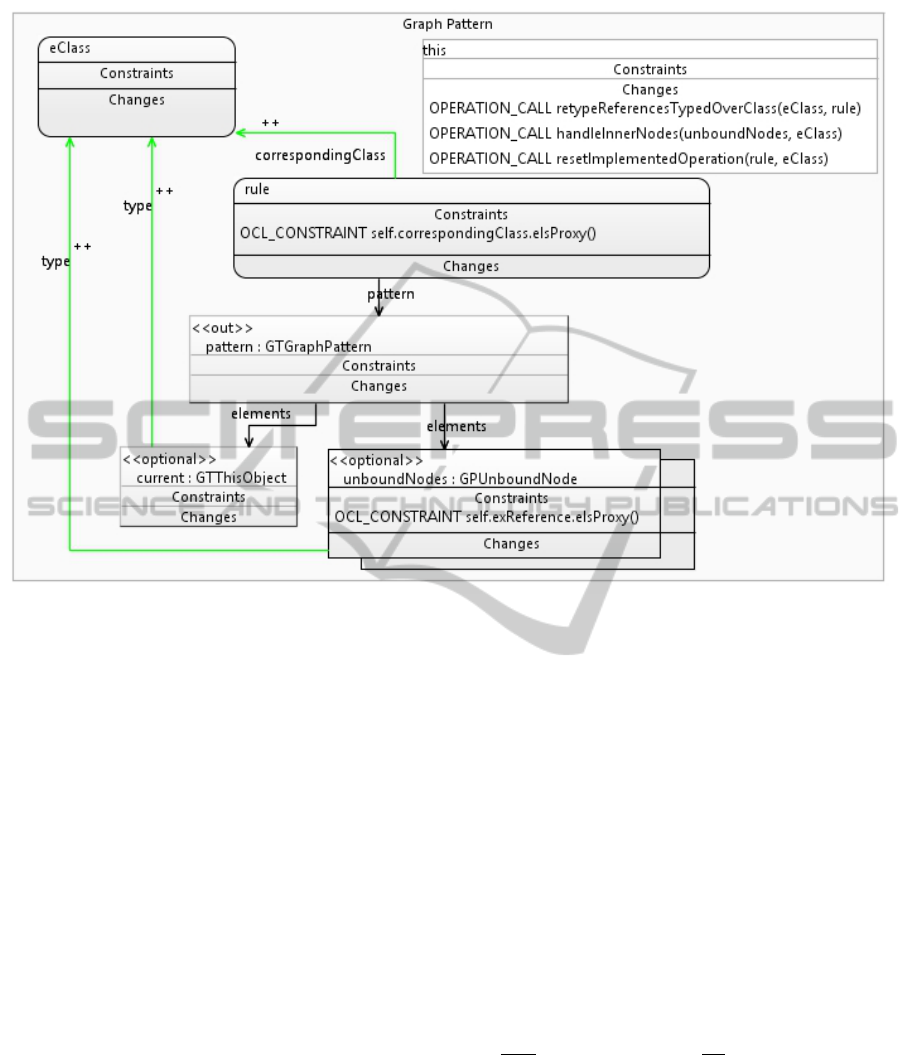
Figure 7: Rule propagating the renaming of a class in the model to the graph transformation rule.

Research on model refactoring primarily focuses

on the structural model (class diagrams). For exam-

ple, in (Biermann et al., 2006) refactoring of Ecore

models is speciﬁed with graph transformation rules in

the AGG environment (Taentzer, 2003). Mens (Mens,

2005) demonstrates how refactoring transformations

on UML class diagrams may be speciﬁed in different

graph transformation languages (AGG and Fujaba).

In (Mens et al., 2007), critical pair analysis is applied

to AGG rules for refactoring Ecore models in order to

detect dependencies between refactoring transforma-

tions. Based on this analysis, the user is guided in the

application of these transformations.

Bottoni (Bottoni et al., 2003) goes beyond these

approaches by providing integrated refactoring trans-

formations: A refactoring transformation is applied

not only to a UML class diagram, but also to the

source code implementing the structural model. Our

work differs from this approach inasmuch as we con-

sider behavioral models rather than source code.

We are aware of only a few approaches dealing

with the propagation of changes from the structural

model into the behavioral model. Rosner and Bauer

(Roser and Bauer, 2008) propose an approach to up-

date model transformations in response to metamodel

changes. The approach requires an ontology mapping

between metamodel versions and is applied to evolve

QVT-R (OMG, 2011) transformations. The evolution

of model transformations constitutes an example of a

higher order transformation (Tisi et al., 2009).

To the best of our knowledge, the only approach

dealing with the propagation of changes into graph

transformation rules is presented in (Levendovszky

et al., 2009), which refers to the GReAT language

and environment (Agrawal et al., 2006). However,

this approach suffers from several limitations. First, it

considers only elementary changes to the metamodel,

e.g., changing the name of a class. Second, changes

are propagated only in a semi-automatic way. Third,

the resulting graph transformation rules may contain

syntactic and semantic errors.

Altogether, the work presented in this paper is

unique inasmuch as it does not only support refactor-

ing with, but also refactoring for graph transformation

rules. Refactoring on the structural and the behav-

ioral model are supported in an integrated way, and

changes are propagated to graph transformation rules

such that consistency is preserved.

ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends

7 CONCLUSION

Model-driven software engineering reduces develop-

ment effort by replacing low-level programming with

the construction of high-level models. To make

these models executable, structural modeling has to

be complemented with behavioral modeling. During

their lifetime, models undergo many changes for a va-

riety of different reasons. Thus, it is crucial to sup-

port model evolution. Refactoring of models provides

an important contribution to model evolution since it

aims at restructuring models such that future changes

are facilitated.

In this paper, we presented tool support for model

refactoring in the ModGraph environment. Mod-

Graph employs Ecore models for structural modeling

and graph transformation rules for behavioral mod-

eling. Refactorings are supported in an integrated

way: Each refactoring transformation on the struc-

tural model is consistently propagated into the be-

havioral model. In this way, our work goes con-

siderably beyond previous work on model refactor-

ing which was conﬁned to the refactoring of the

structural model. Furthermore, while several other

approaches use graph transformations for refactor-

ing (i.e., refactoring with graph transformations), our

work is unique inasmuch as it addresses refactoring

for graph transformations, as well.

REFERENCES

Agrawal, A., Karsai, G., Neema, S., Shi, F., and Vizhanyo,

A. (2006). The design of a language for model trans-

formations. Software and System Modeling, 5(3):261–

288.

Banerjee, J., Kim, W., Kim, H.-J., and Korth, H. F. (1987).

Semantics and implementation of schema evolution in

object-oriented databases. In Proceedings of the 1987

ACM SIGMOD International Conference on Manage-

ment of Data (SIGMOD 1987), pages 311–322, San

Franciso, CA. ACM Press.

Biermann, E., Ehrig, K., K

ohler, C., Kuhns, G., Taentzer,

G., and Weiss, E. (2006). EMF model refactoring

based on graph transformation concepts. In Favre, J.-

M., Heckel, R., and Mens, T., editors, Proceedings of

the Third Workshop on Software Evolution Through

Transformations: Embracing the Change, volume 3

of Electronic Communications of the EASST, Natal,

Rio Grande del Norte, Brazil. 16 p.

Bottoni, P., Parisi-Presicce, F., and Taentzer, G. (2003).

Specifying integrated refactoring with distributed

graph transformations. In (Pfaltz et al., 2003), pages

220–235.

Buchmann, T., Westfechtel, B., and Winetzhammer, S.

(2012). ModGraph: Graphtransformationen f

ur EMF.

In Sinz, E. J. and Sch

urr, A., editors, Modellierung

2012, volume 201 of Lecture Notes in Informatics,

pages 107–122, Bamberg, Germany. GI.

ummel, N. (2013). Refactoring mit Graphtransforma-

tionsregeln. Bachelor thesis, University of Bayreuth,

Bayreuth, Germany.

Fowler, M. (1999). Refactoring: Improving the Design of

Existing Code. Addison-Wesley, Boston, MA, USA.

Geiger, L. (2008). Graph transformation-based refactor-

ings using Fujaba. In Rensink, A. and van Gorp, P.,

editors, 4th International Workshop on Graph-Based

Tools: The Contest, Leicester, UK.

Levendovszky, T., Balasubramanian, D., Narayanan, A.,

and Karsai, G. (2009). A novel approach to semi-

automated evolution of DSML model transformation.

In van den Brand, M., Gasevic, D., and Gray, J., edi-

tors, Proceedings of the Second International Confer-

ence on Software Language Engineering (SLE 2009),

volume 5969 of LNCS, pages 23–41, Denver, CO.

Springer.

Mens, T. (2005). On the use of graph transformations

for model refactoring. In L

ammel, R., Saraiva, J.,

and Visser, J., editors, International Summer School

on Generative Techniques in Software Engineering

(GTTSE 2005), volume 4143 of LNCS, pages 219–

257, Braga, Portugal. Springer.

Mens, T., Eetvelde, N. V., Demeyer, S., and Janssens, D.

(2005). Formalizing refactorings with graph transfor-

mations. Journal of Software Maintenance and Evo-

lution: Research and Practice, 17(4):247–276.

Mens, T., Taentzer, G., and Runge, O. (2007). Analysing

refactoring dependencies using graph transformation.

Software and Systems Modeling, 6(3):269–285.

Mens, T. and Tourw

e, T. (2004). A survey of software refac-

toring. IEEE Transactions on Software Engineering,

30(2):126–139.

OMG (2011). Meta Object Facility (MOF) 2.0

Query/View/Transformation Speciﬁcation. Object

Management Group, Needham, MA, formal/2011-01-

01 edition.

Pfaltz, J. L., Nagl, M., and B

ohlen, B., editors (2003).

Application of Graph Transformations with Industrial

Relevance: Second International Workshop (AGTIVE

2003), volume 3062 of LNCS, Charlottesville, VA,

USA. Springer.

Rose, L. M., Herrmannsdoerfer, M., Williams, J. R.,

Kolovos, D., Garc

es, K., Paige, R. F., and Pollack,

F. A. (2010). A comparison of model migration tools.

In Petriu, D. C., Rouquette, N., and Haugen, Ø., ed-

itors, MODELS 2010, Part I, volume 6394 of LNCS,

pages 61–75, Oslo, Norway. Springer.

Roser, S. and Bauer, B. (2008). Automatic generation and

evolution of model transformations using ontology en-

gineering space. In Spaccapietra, S., Pan, J. Z., Thi-

ran, P., Halpin, T., Staab, S., Svatek, V., Shvaiko,

P., and Roddick, J., editors, Journal of Data Seman-

tics XI, volume 5383 of LNCS, pages 32–64. Springer,

Heidelberg.

Steinberg, D., Budinsky, F., Paternostro, M., and Merks,

E. (2009). EMF: Eclipse Modeling Framework.

Addison-Wesley, Boston, MA, 2nd edition.

PropagatingModelRefactoringstoGraphTransformationRules

Taentzer, G. (2003). AGG: A graph transformation envi-

ronment for modeling and validation of software. In

(Pfaltz et al., 2003), pages 446–453.

Tisi, M., Jouault, F., Fraternali, P., Ceri, S., and B

ezivin,

J. (2009). On the use of higher-order model transfor-

mations. In Paige, R. F., Hartman, A., and Rensink,

A., editors, ECMDA-FA 2009, volume 5562 of LNCS,

pages 18–33, Heidelberg. Springer.

Winetzhammer, S. (2012). ModGraph — generating exe-

cutable EMF models. In Krause, C. and Westfechtel,

B., editors, Proceedings of the 7th International Work-

shop on Graph Based Tools, volume 54 of Electronic

Communications of the EASST, pages 32–44, Bremen,

Germany. EASST.

Winetzhammer, S. and Westfechtel, B. (2013). ModGraph

meets Xcore: Combining rule-based and procedural

behavioral modeling for EMF. In Tichy, M., Ribeiro,

L., Margaria, T., Padberg, J., and Taentzer, G., edi-

tors, Proceedings of the 12th International Workshop

on Graph Transformation and Visual Modeling Tech-

niques (GTVMT 2013), volume 58 of Electronic Com-

munications of the EASST, Rome, Italy. EASST.

Winetzhammer, S. and Westfechtel, B. (2014). Compil-

ing graph transformation rules into a procedural lan-

guage for behavioral modeling. In Pires, L. F., Ham-

moudi, S., Filipe, J., and das Neves, R. C., edi-

tors, Proceedings of the 2nd International Conference

on Model-Driven Engineering and Software Devel-

opment (MODELSWARD 2014), pages 415–424, Lis-

bon, Portugal. SCITEPRESS Science and Technology

Publications, Portugal.

undorf, A. (2001). Rigorous object oriented software de-

velopment. Technical report, University of Paderborn,

Germany.

ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends