A Comprehensive Evaluation Model for BASE Transaction Processing

Sachi Nishida and Yoshiyuki Shinkawa

Graduate School of Science and Technology, Ryukoku University,

1-5 Seta Oe-cho Yokotani, Otsu, Shiga, Japan

Keywords:

Data Integrity, Colored Petri Net, Cloud Computing, Transaction Processing.

Abstract:

Transaction processing has been thought to be not suitable for cloud computing. The primary reason is that the

data integrity principle is much relaxed from the traditional ACID. This new principle is known as BASE. In

order to deploy transaction processing systems over cloud environments, we need to reveal the characteristics

of transaction behavior under the BASE principle. The paper proposes a CPN (Colored Petri Net) based

comprehensive integrity evaluation model with high modularity, which can easily be customized, or enhanced

for diverse application domains and cloud environments.

1 INTRODUCTION

Cloud computing is recently used in many applica-

tion domains as a ﬂexible, highly available, scalable,

and low-cost platform. However, most applications in

this environment are so-called non-mission-critical or

ad-hoc ones, whereas one of the most high-volume

applications is the database transaction processing,

which is thought to be not suitable for cloud com-

puting. The major reason for this unsuitability is

“data integrity”, which traditional database and trans-

action systems have regarded as the most important

issue. In these systems, the principle for the data

integrity is called “ACID”, standing for Atomicity,

Consistency, Isolation, and Durability (Weikum and

Vossen, 2001). This principle requires fully isolated

operations on databases for data integrity.

On the other hand, cloud computing adopts more

relaxed principle for data integrity, being referred to

as BASE, standing for Basically Available, Soft state,

and Eventually consistent (Pritchett, 2008). In or-

der to deploy database transaction systems over cloud

computing environments, we ﬁrst have to reveal how

the characteristics of the BASE principle affect the

data integrity in transaction processing. Since the

BASE principle allows non-isolated concurrent ac-

cess to databases, the behavior of BASE transac-

tions becomes much more complicated than tradi-

tional ACID ones. Therefore, it seems unrealistic to

evaluate the data integrity logically, considering all

the possible data access patterns. Instead, it seems re-

alistic to evaluate it through simulation using accurate

BASE transaction models.

The simulation model must represent the function-

ality and behavior of both the cloud platform and ap-

plication programs for the transactions. While the

platform is common among diverse application do-

mains, each application program is unique to a spe-

ciﬁc domain. In order to make the model comprehen-

sive to deal with many kinds of different domains, it

should be built in high modularity, so that the domain

unique parts can easily be plugged in or out.

This paper proposes a simulation based evaluation

model for data integrity in cloud transaction process-

ing. For the modeling and simulation, Colored Petri

Net (CPN) is used, since it can express complicated

concurrent systems from behavioral, functional, and

structural viewpointssimultaneously with high modu-

larity. The rest of the paper is organized as follows. In

section 2, we discuss the characteristics of the behav-

ior of the BASE transactions, along with the concept

of data integrity in generalized transaction process-

ing. In addition, CPN based evaluation framework is

introduced. Section 3 presents how the BASE trans-

action processing platform and application logic are

modeled and integrated using CPN. Section 4 shows

the mechanism and algorithm for the evaluation of the

data integrity in the above CPN models.

2 CLOUD TRANSACTION

MODEL FOR DATA INTEGRITY

In the cloud environments, data integrity shows

393

Nishida S. and Shinkawa Y..

A Comprehensive Evaluation Model for BASE Transaction Processing.

DOI: 10.5220/0005099703930400

In Proceedings of the 9th International Conference on Software Engineering and Applications (ICSOFT-EA-2014), pages 393-400

ISBN: 978-989-758-036-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

the different facets from traditional database transac-

tion processing. Before discussing the integrity eval-

uation, we ﬁrst reveal the characteristics of the cloud

regarding data integrity

2.1 Data Integrity in the Cloud

Data integrity is one of the most important issues in

traditional database transaction processing, or trans-

action processing in short. The ACID principle as-

sures the isolated access to databases for each transac-

tion, in order to prevent unintentional concurrent up-

dates on the same entry in a database, which might

break the data integrity.

This rigorous control for the data integrity often

reduces the performance and throughput of the trans-

action processing, because of the locking and serial-

ization overhead. On the other hand, cloud computing

is aiming for rather high availability and scalability,

and therefore “ACID” principle is regarded as con-

ﬂicting with the goal of cloud computing.

In order to adapt transaction processing to cloud

computing, a more relaxed principle for data integrity

is proposed, which is often referred to as “BASE”.

Following the BASE principle, transactions in the

cloud environments show the different behavior from

traditional ones, because of its unique integrity preser-

vation mechanism.

Therefore, if we plan to run transactions in cloud

environments, we need to understand their behavioral

characteristics from the data integrity viewpoint. In

order to understand it rigorously, we should formalize

the concept of data integrity, along with its preser-

vation mechanism. The data integrity is mainly an

application oriented matter, and could be differently

deﬁned among application domains. Therefore, there

seems no way to give the common deﬁnition of it. In-

stead, it seems more practical to deﬁne the standard-

ized notation for data integrity rules or constraints.

One of the rigorous ways to express these

constraints is to use the predicate logic formulae

(Shinkawa and Matsumoto, 2001)(Shinkawa, 2012).

Since the logic formulae for data integrity deﬁne the

constraints on database values, the domain of dis-

course is composed of

D = (

[

) ∪(

[

i, j

) ∪(

[

i, j,k

(k)

i, j

)

where D

is the i-th database, r

is the j−th entry or

record in the database D

, and a

(k)

is the k-th attribute

of the r

In addition to this domain of discourse, we have

to deﬁne the functions, predicates, variables, and con-

stants rigorously. Assuming we have deﬁned all these

elements of the logic, any constraints on the databases

can be represented by a prenex conjunctive normal

form (PCNF) as

···Q



(ij)

···t

(ij)

)



where Q

is a variable with the quantiﬁer “∀” or “∃”,

e.g. ∀x

or ∃x

, P

is a predicate, and t

(ij)

is a

term composed of variables, constants, and functions

(Schoening, 2008).

On the other hand, the mechanism for preserving

data integrity in the cloud is an implementation of the

BASE principle, and is equivalent to the optimistic

locking (Kung and Robinson, 1981). This mechanism

allows arbitrary concurrent access to any entry in the

databases, and the integrity preservation is attempted

only at the commit point, examining whether the re-

ferred entries have been modiﬁed during the transac-

tion execution.

The concurrent database access makes the behav-

ior of the transactions more complicated than the

ACID ones, since all the database references and up-

dates might be interleaved between the transactions.

In order to evaluate the data integrity for such a com-

plicated transaction behavior, a simulation approach

is more suitable than logical analysis.

2.2 CPN Based Integrity Evaluation

Model

For effective and efﬁcient simulation, we need to

build an executable model reﬂecting the behavior

and functionality of all the related transactions, along

with the cloud platform structure including databases.

Therefore, we have to select a modeling tool having

the capability for expressing the three orthogonal as-

pects of a system simultaneously, namely, the func-

tional, behavioral, and structural aspects. In addition,

the created models must be executable for simulation.

For these requirements, Colored Petri Net (CPN) is

one of the most suitable modeling tools, since it ex-

tends Petri Net from functional viewpoint, which can

express the behavior and the structure of systems pre-

cisely (Jensen and Kristensen, 2009) (Jensen et al.,

2007).

CPN is formally deﬁned as a nine-tuple CPN=(P,

T, A, Σ, V, C, G, E, I) , where

P : a ﬁnite set of places.

T : a ﬁnite set of transitions.

(a transition represents an event)

A : a ﬁnite set of arcs P∩ T = P∩ A = T ∩ A =

Σ : a ﬁnite set of non-empty color sets.

(a color represents a data type)

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

394

V : a ﬁnite set of typed variables.

C : a color function P → Σ.

G : a guard function T → expression.

(a guard controls the execution of a transition)

E : an arc expression function A → expression.

I : an initialization function : P → closed expression.

In order to make the model comprehensive and

reusable, modularity is the key to build it. In this pa-

per, we focus on the two types of modularity in build-

ing the model. One is the modularity in the evaluation

process, and the other is that in transaction execution.

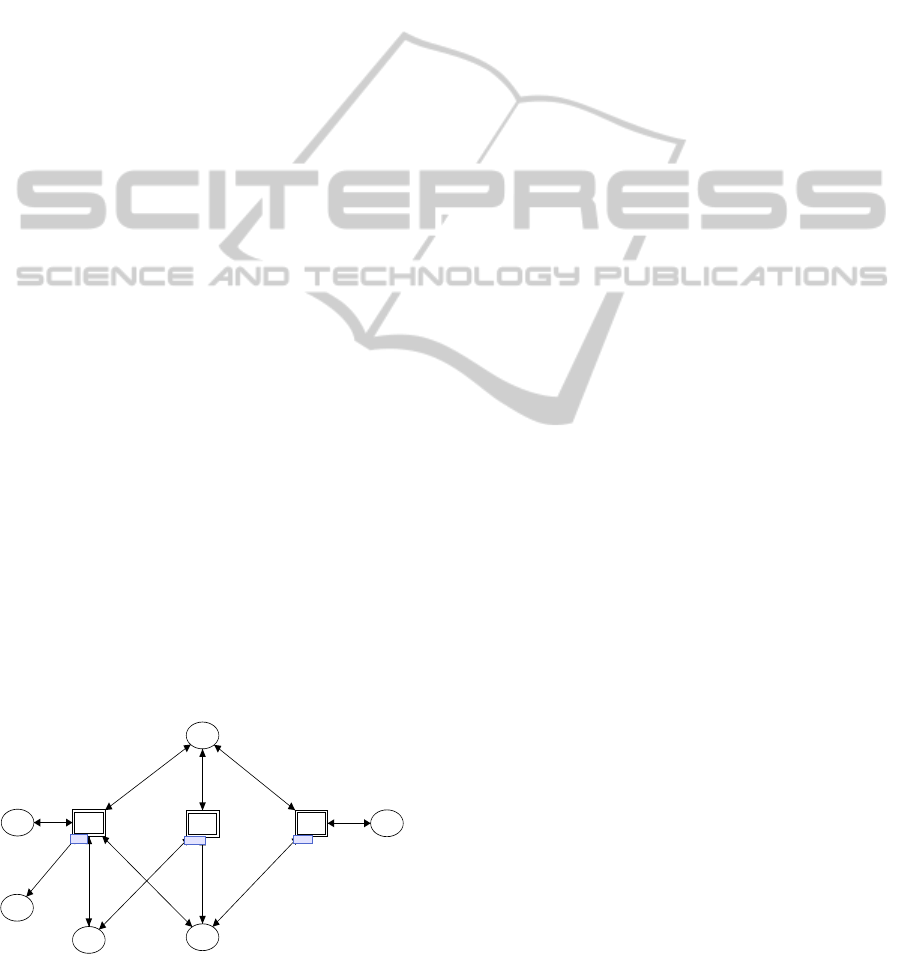
The ﬁrst modularity is implemented as the CPN

model that is composed of serially-connected three

major modules as shown in Figure 1. In this ﬁgure,

each double-lined rectangle represents a module in

the form of a CPN hierarchical substitution transition

including the detailed CPN model inside. The second

modularity is implemented by separating the appli-

cation unique part from the common functional part.

This modularity is discussed in the next section.

In Figure 1, the “INIT” module initializes the

whole model by marking the places with initial to-

kens. These tokens are generated by this module

according to the tokens in the “DBIP” and “TRIP”

places, which mean Database Initialization Param-

eter and Transaction Initialization Parameter. The

“EXEC” module performs the database updates by

simulating the behavior and functionality of each

transaction according to the cloud platform character-

istics embedded in the module. The “EVAL” module

evaluates the simulation results by examining the to-

kens marked in the database place “DBBody”. Each

model represents a phase in the integrity evaluation

process, and is controlled by the token in the “PC”

(Phase Control) place.

EXEC

EVAL

INIT

RST

DBBody

TRA

TRIP

DBIP

INIT

EVAL

EXEC

Figure 1: Top Level CPN Model.

3 CPN BASED CLOUD

TRANSACTION MODEL

For the data integrity evaluation in the cloud, we ﬁrst

need to build a simulation model reﬂecting the cloud

characteristics of both the platform and application.

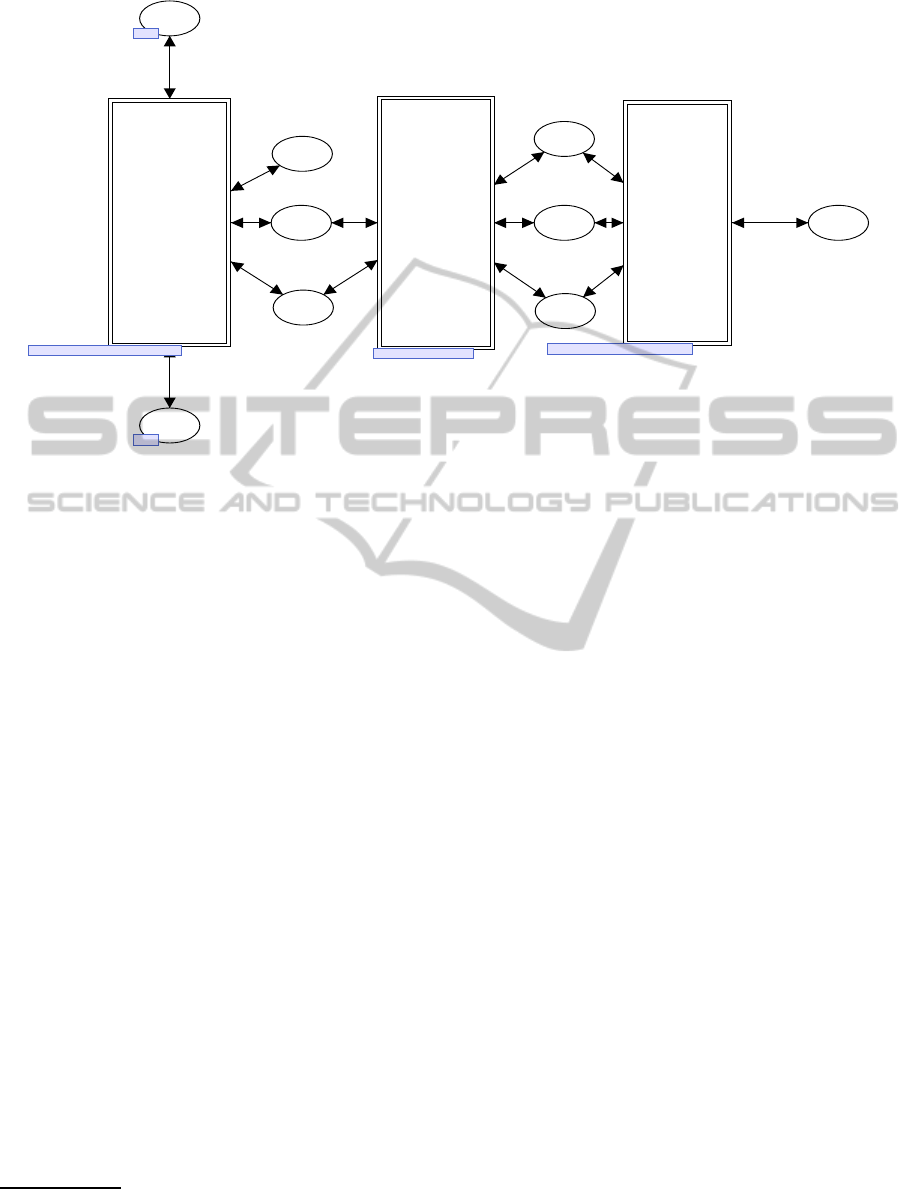
This model is designated by the “EXEC” module in

Figure 1. The purpose of the “EXEC” module is

to simulate the behavior and functionality of each

transaction based on the cloud platform characteris-

tics. Since transaction processing is logically com-

posed of three major functional components, namely,

“scheduling”, “application logic”, and “database ac-

cess”, we build the “EXEC” module with three func-

tional sub-modules, namely, “Scheduling”, “Applica-

tion”, and “Database” as shown in Figure 2.

3.1 Scheduling Sub-module

The “Scheduling” sub-module throws transactions

into the system, maintaining appropriate concurrency

level. In order to control the concurrency level, this

module uses an integer list “COMPA”, each element

of which represents the thread availability. The ele-

ment value of “0” means an available thread, while

the value of “1” means a busy thread. This sub-

module works as follows.

1. Examine the token in the place “COMPA”

whether there is an available thread.

2. If there is an available thread, put a transaction

token into the place “Q”, extracting it from the

place “TRA”. Otherwise, wait until there is an

available thread.

3. When one of the transaction running in the “Ap-

plication” sub-module terminates, set “0” to the

corresponding element of the “COMPA” token.

The “Scheduling” sub-module is common among

all the application domains. The only customizable

point is the COMPA token which represents the con-

currency level.

3.2 Application Sub-module

The second sub-module “Application” simulates each

application logic. Therefore it is application domain

unique, and must be built for each application. From

data integrity viewpoint, a transaction is regarded as

a series of database access requests. Consequently

it seems natural to express a transaction as a series

of transitions, each of which generates a token for

database access. However, the sequence and the con-

tent of database access requests may vary with the ar-

guments of the transaction passed at its starting time,

AComprehensiveEvaluationModelforBASETransactionProcessing

395

Database

Sub-module

Database Sub-module

Scheduling

Sub-module

Scheduling Sub-module

Application

Sub-module

AP sub-module

COMPD

DBRL

DBB

Version

VER

COMPA

Arglist

I/O

TRA

I/OI/O

I/O

AP sub-module

Scheduling Sub-module

Database Sub-module

DBBody

Figure 2: EXEC Modulel.

or with the database values that have been read during

the execution. In addition, the sequence includes the

control structures like if-then-else branches and while

loops. Taking the above conditions into account, we

compose the “Application” sub-module as follows.

As shown in Figure 3, the “Application” sub-

module is composed of a series of transitions sharing

the places “COMPD”, “DBB”, “DBRL”, and “ARG”

. The place “COMPD” serializes the transition ﬁr-

ings, along with interfacing with the “Database” sub-

module. This place is associated with the color set

closet COMPD = product TID * VER *

SEQ * OP * RC;

where “SEQ” designates the transition sequence num-

ber to be ﬁred. Each transition is assigned a unique se-

quence number, and it examines this ﬁeld by its guard

function. The place “DBRL” contains a set of tokens

each of which represents a list of database access re-

quest tokens “DBR” from a speciﬁc transition. The

“DBR” has the color set

colset DBR = TID * VER * SEQ * OP *

DBID * KEY * AttList;

where “OP” represents the operation on the database

“DBID” by the key value “KEY” and the attribute val-

ues “AttList”. The place “DBB” works as a database

buffer for the database operations, and contains the

accessed database entries in the form of lists. The

place “ARG” contains the arguments or parameters of

the transaction. These arguments determine the appli-

In order to avoid crossing arcs, the ﬁgure uses fusion

places. The places with the same tag designate the same

single place.

cation logic. The place “Q” contains the transaction

tokens with the color set

closet TRAN = product TID * VER * ArgList;

where TID is a unique transaction id, and VER is a

version to express the timestamp, which will be dis-

cussed later in conjunction with optimistic locking.

The transitions are “L

”, “LS

”, “LE

”, “TE”, and

“TF”. “L

” represents a single database access op-

eration, possibly including the if-then-else structure.

“LS

” and “LE

” represent the starting and ending

points of a loop structure respectively. “LE” and

“LF” represent the transaction end and ﬁnalization

processes respectively.

Using the above places and transitions, the sub-

module works as follows.

1. Obtain the transaction token with the proper

“TID” from the “Q” place.

2. The ﬁrst transition set the “SEQ” ﬁeld value of

the token “COMPD” with “1”. This value is in-

cremented by the “Database” sub-module, so that

the next transition becomes eligible to ﬁre.

3. If the ﬁring transition is “L

” or “LS

”, a database

access token “DBR” is appended to the “DBRL”

token.

4. If the ﬁring token is “LE

”, it sets the “SEQ” ﬁeld

value of the “COMPD” token with either the se-

quence number of “LS

” or “++SEQ”, according

to the loop condition.

5. If the ﬁring transition is “TE”, perform the end-

of-transaction process. Usually, it depends on the

application requirements, e.g. deleting some work

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

396

LC3

LS2

ARG

DBRL

DBB

DBRL

DBB

DBRL

DBB

DBB DBRL

DBB

DBRL

DBB

DBRL

ARG

COMPD

DBB

DBBDBB

DBRL

DBRLDBRL

L4 ARG

ARGARG

TFARG

ARGARG

DBRL

DBRLDBRL

DBB

DBBDBB

ARG

ARGARG

TE ARG

ARGARG

DBRL

DBRLDBRL

DBB

DBBDBB

LE5 ARG

ARGARG

DBB

DBBDBB

COMPA

DBRL

DBRLDBRL

DBB

DBBDBB

Figure 3: Application Sub-module.

entries in the databases.

6. If the ﬁring transition is “TF”, perform the ﬁnal-

ization process of the transaction. It deletes the

related elements in the “ARG”, “COMPD”, and

“DBRL” tokens. In addition, reset a busy entry of

the “COMPD” token to “0”, that is, to available.

Since this sub-module represents a speciﬁc applica-

tion logic, a unique instance must be built for each

application. The structure of each instance is basi-

cally the same. Each instance is assigned an unique

“TID” (a transaction id).

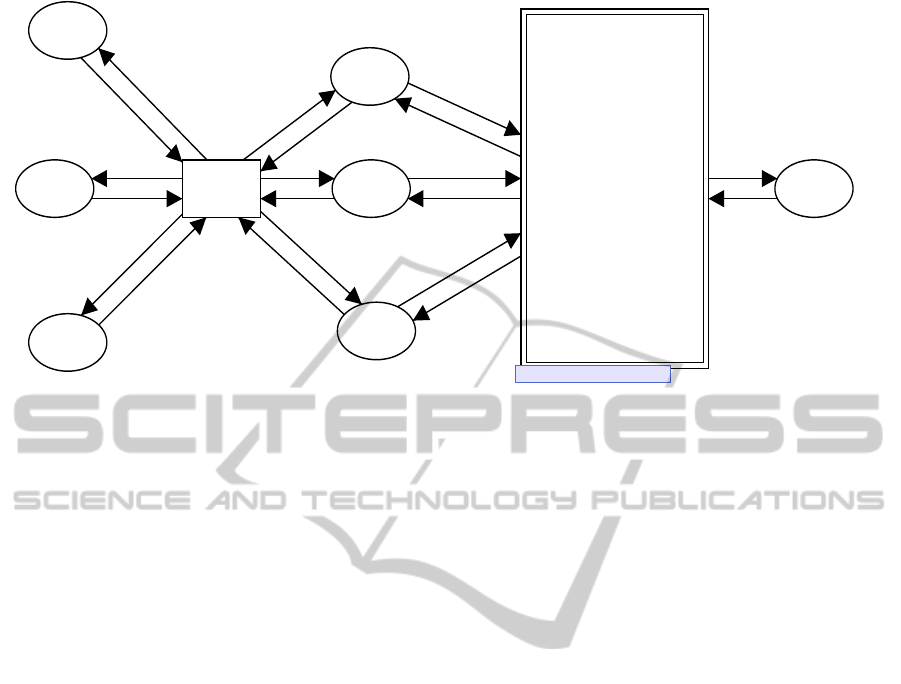
3.3 Database Sub-module

Each time a transition in the “Application” sub-

module marks a token for the database access re-

quest, “Database” sub-module is activated to process

it. In order to simulate the concurrent access to the

databases, this sub-module consists of multiple in-

stances for each database. All the instances have the

same structure as shown in Figure 4, and work as fol-

lows.

1. The ﬁrst transition examines the value of the ﬁeld

“DBID” in the “DBR” token to determine whether

the request is directed toward this instance.

2. According to the value of the “OP” ﬁeld in

DBR, one of the conﬂicting transitions “READ”,

“WRITE”, or “COMMIT” is ﬁred, which per-

forms database read, write or commit operation

respectively. The value of “OP” ﬁeld is deﬁned

as “1” (select), “2” (update), “3” (insert), “4”

(delete), or “5”(commit).

3. The “READ” transition of the ith instance

searches for the token with the given “KEY” in

the “DBBody

” place, which consists of a list of

database entries. If found, append the database

entry to the list token in “DBB” place, other-

wise do nothing. The DBB place works as a

database buffer for each transaction thread. Then

set the operation result code in the “RC” ﬁeld of

“COMPD” ﬁeld.

4. The “WRITE” transition also search the place

“DBBody

” for the designated key in the same

way as “READ”. If found, in case of “OP = 2”

or “OP = 4”, that is, for the update or delete op-

eration, append the DBR token to the list in the

“DBB” place. On the other hand, in case of “OP

= 3”, that is, for the insert operation, do noth-

ing. Then set the result code in the same way as

“READ”. If not found, only the insert operation

is performed.

5. The “COMMIT” transition performs the commit

process that ﬁnalizes the database modiﬁcation re-

quest on the database, which is implemented as

the place “DBBody

”. This process follows the

optimistic locking mechanism stated below.

The basic operation of the optimistic locking is to

ensure that “no other transactions update the database

entries that have been referred to during this trans-

action scheduling. In order to identify transactions

that update the speciﬁc database entries, we prepare

a common place “WSET among the “Database sub-

module instances, which includes the token repre-

senting the history of database updates by the trans-

actions. This token is expressed as a list of each

database update with the associated transaction infor-

mation. The list element has the color set

colset WSETE = product TID * VER *

DBID * KEY * AttList

AComprehensiveEvaluationModelforBASETransactionProcessing

397

COMMIT

WRITE

READ

result

dbr

DBB

DBRL

updateDBRL

COMPD

compd

updateDBB

dbr

Database

Process

Database ProcessDatabase Process

dbr

result

dbr

result

dbr

result

DBBody

dbbe

updateCOMPD

dbb

Figure 4: Database Sub-module.

This element is appended to the token after the suc-

cessful comit.

The “COMMIT” process examines the “WSET”

list whether it has the element that satisﬁes

1. The “KEY” ﬁeld value is identical to that of an

“DBB” element with “OP = 1”, namely, an entry

that has been read from a database.

2. The “VER” (version) value v satisﬁes v

< v < v

where v

is the “VER” value assigned to the cur-

rently committing transaction, and v

is the cur-

rent “VER” value.

If the same key is found, the transaction is aborted,

otherwise it is committed.

In case of “commit, “WSETE token is created and

appended to the “WSET token, by extracting the DBB

elements with the OP ﬁeld of “2”, “3”, or “4”. In this

process, the “VER” value is changed to “v

”. Then

the “write elements in the DBB token are moved to

the “DBBody

” place to reﬂect the database update.

On the other hand, in case of “abort, all the updates in

DBB token are discarded. In both cases, the COMPD

token is modiﬁed to indicate that the transaction has

been committed or aborted.

As discussed so far, the modularity of the “EXEC”

module is a bit complicated. The module consists of

three sub-modules. Two of them, namely, “Schedul-

ing” and “Database” are common among application

domains, and therefore non-customizable. On the

other hand, “Application” sub-module is unique for

each application, and therefore is fully customizable.

4 CPN BASED DATA INTEGRITY

EVALUATION

After the simulation of the model that was built in the

previous section is completed, the database tokens are

updated according to the initial database state, the ap-

plication logic, and the concurrency control that are

performed on the actual cloud platform being consid-

ered.

In order to perform the simulation , we have to

prepare the appropriate sets of databases and transac-

tions in the form of CPN tokens. As for the databases,

they should reﬂect the actual database characteristics,

in terms of database schema and key/attribute distri-

bution.

For simulation convenience, we assume all the

keys and attributes are expressed by integers. There-

for a database record can be expressed as a tuple of

integers. However, since the number of attributes is

variable, they are packed into a list, and a database

entry is a tuple of a key and an attribute list. As a

color set, a database entry and database itself are ex-

pressed as

closet DBRec = product KEY * AttList;

closet DBBody = product DBID * DBRecL;

where “AttList” is a list of attributes, “DBRecL” is a

list of “DBRec”, and “DBID” represents a database

identiﬁer.

On the other hand, a transaction has a more simple

form, namely, is composed of a a pair of a transac-

tion id and an argument list. For the same reason as

databases, we assume transaction id and argument list

are also expressed in the form of integers.

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

398

As stated in section 3, these database and trans-

action tokens are generated by the “INIT” module in

Figure 1.

DBBody1

DBBody2

DBBody3

Figure 5: EVAL Module.

When generating a database token, the distribu-

tion of the key values and attribute values must be as

similar as possible to the actual database to be mod-

eled. In order to realize this requirement, the database

generation transition “GENDB” is designedto receive

the initialization parameters including the information

on the probabilistic distribution. This information is

expressed as a color set

closet GenInfo = product KEY * KEY *

MEAN * VAR * FUNC;

where the ﬁrst two elements represent the key value

range, “MEAN” represents the mean value of the

key values, “VAR” represents the variance of the key

distribution, and “FUNC” represents the distribution

function that the key values follow. The “FUNC” val-

ues are currently deﬁned as

1. uniform distribution

2. normal distribution

3. exponential distribution

, however, we can easily add a new distribution func-

tion from the CPN ML library. The arc function on

the arc from the transition “GENDB” to the place

“DBBody

” use the above information to generate the

database transitions.

As for transaction generation, we need the infor-

mation on the transaction mix and the probabilistic

distribution of the argument values. Such informa-

tion can be implemented in the similar way to the

databases discussed above.

After all the needed databases and transactions are

generated in the form of tokens by the “INIT” module,

the “EXEC” module commences to update the gener-

ated databases by simulating the behavior and func-

tionality of the generated transactions. When all the

generated transactions are committed or aborted, the

“EVAL” module is initiated. This module has rather

simpler structure than other two modules, as shown in

Figure 5.

As stated in section 2, the data integrity is de-

ﬁned as a set of predicate logic formulae {P

}. For

each P

, an evaluation transition E

is located be-

tween the database places DBBody

s and the place

“IV” which holds the evaluation result token with

the color set “IV”. The color set “IV”, stand-

ing for integrity vector, is a pair of integer lists

([c

, c

, ·· · , c

], [r

, r

, ·· · , r

]), where n is the num-

ber of the constraint logic formulae, c

represents the

completion of integrity evaluation for the formula P

If c

= 1, the r

represents the evaluation result for the

formula P

. The evaluation process works as follows.

1. Mark the initial token ([0, 0, ··· , 0], [0, 0, ··· , 0]) at

the place “IV”.

2. When the evaluation process starts, each E

tran-

sition examines the value of c

. If c

= 0, then

examine the database places DBBody

s whether

they satisfy the formula P

3. If the P

is NOT satisﬁed, then set “r

= 1”, else

set “r

= 0”.

4. set “c

= 1”.

After all the logic formulae are evaluated, that is, “IV”

token becomes ([1, , 1, ·· · , 1], [r

, r

, ·· · , c

]), the sec-

ond element indicates whether the data integrity is

preserved by the transaction executions. If r

= 1

holds, it means the ith constraint formula P

is not

satisﬁed. In such case, the transactions must be re-

considered from the application and cloud platform

viewpoints.

5 CONCLUSIONS

The BASE is a new concept for data integrity for

transaction processing in cloud environments. In or-

der to deploy newly developedor currently used trans-

action systems over cloud environments smoothly, we

need to evaluate the systems from the data integrity

viewpoint, since the BASE is too different concept

from the traditional ACID. This paper introduced a

CPN based BASE transaction evaluation model with

high modularity and simulation capability.

In order to make the model comprehensive, the

model is composed of three major modules based

on the evaluation process, namely, data generation

phase, model execution phase, and integrity check-

ing phase. In addition, the model is divided into two

parts, that is, common functionality part and applica-

tion unique part.

AComprehensiveEvaluationModelforBASETransactionProcessing

399

The above model characteristics make it possi-

ble to plug-in any application model to the proposed

model, or to plug-out any unnecessary one. There-

fore, we can evaluate many kinds of applications to

run in cloud environments at lower cost than prepar-

ing the exclusive models for them.

The data integrity in this paper is assumed to be

expressed in the form of the ﬁrst order predicate logic

formulae, however there could be other forms of in-

tegrity constrains, e.g. those expressed in the form of

modal logic like temporal logic, or those by higher

order logic. For these enhancements, we need to

develop more CPN ML codes to handle these con-

straints.

The paper focused on the generalized BASE trans-

action processing, which can commonly be applicable

to any cloud environments. However, each environ-

ment, e.g. Google App Engine (Sanderson, 2009) or

Amazon EC2 (van Vliet and Paganelli, 2011) has its

own options. In order to reﬂect such options, more

platform oriented models are needed.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Grant

Number 25330094.

REFERENCES

Jensen, K. and Kristensen, L. (2009). Coloured Petri

Nets: Modeling and Validation of Concurrent Sys-

tems. Springer-Verlag.

Jensen, K., Kristensen, L. M., and Wells, L. (2007).

Coloured Petri Nets and CPN Tools for Modelling

and Validation of Concurrent Systems. In Inter-

national Journal on Software Tools for Technology

Transfer (STTT) Volume 9, Numbers 3-4, pages 213–

254. Springer-Verlag.

Kung, H. T. and Robinson, J. T. (1981). On Optimistic

Method for Concurrency Control. In ACM Transac-

tions on Database Systems (TODS) Volume 6 Issue 2,

pages 213–226. ACM.

Pritchett, D. (2008). BASE: An ACID alternative. In ACM

QUEUE Volume 6 Issue 3, pages 48–55. ACM.

Sanderson, D. (2009). Programming Google App Engine.

Oreilly & Associates Inc.

Schoening, U. (2008). Logic for Computer Scientists (Mod-

ern Birkhaeuser Classics). Birkhaeuser Boston.

Shinkawa, Y. (2012). CPN Based Data Integrity Evalua-

tion for Cloud Transactions. In Proc. 6rd International

Conference on Software Paradigm Trends, pages 267–

272.

Shinkawa, Y. and Matsumoto, M. (2001). An Informa-

tion System View of Consistency and Integrity in En-

terprise Operations. In Proc. 3rd International Con-

ference on Enterprise Information Systems Volume 2,

pages 709–716.

van Vliet, J. and Paganelli, F. (2011). Programming Amazon

EC2. Oreilly & Associates Inc.

Weikum, G. and Vossen, G. (2001). Transactional Informa-

tion Systems: Theory, Algorithms, and the Practice of

Concurrency Control and Recovery. Morgan Kauf-

mann.

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

400