
Multiobjective Optimisation by PSO for Switched Reluctance Motor
(SRM) Drive
Jayanta Mukherjee
1
and Sumana Chowdhuri
2
1
Kalynai Polytechnique College, Westbengal, India
2
Department of Applied Physics, University of Calcutta, Kolkata, India
Keywords: Torque Ripple, PI Control, PWM Control, Hysteresis Control, ZN Method, Total Torque Distortion.
Abstract: Switched Reluctance Motor (SRM), which has many advantages like Induction machine exhibits very
nonlinear characteristics and high torque ripple, the only disadvantages of this machine. Its torque ripple is
dependent on the current profile and also on the turn on and turns off angle of phase excitation and the
speed is dependent on the current command. This work presents one of the Heuristic approaches like
Particle Swarm optimization (PSO) to determine the optimum proportional-integral (PI) controller
parameters and turn on and turn off angles, for minimum torque ripple with optimum torque profile SRM
drive. These offline tuning methods are implemented for the model of a SRM in MATLAB. It has been
observed that by optimizing the controller parameters of a SRM drive with PSO the performance of the
controller is improved.
1 INTRODUCTION
Switched Reluctance Motors (SRM) are fast
becoming a popular alternative to Induction Motors
(IM) in the variable speed drive market. Though the
first SRM was built in 1838, it did not find
widespread use until the late 1970’s. This was due to
the difficulty in controlling the machine. Since the
1960’s, with the advent of power electronics and
high power semiconductor switches, control of the
SRM has become much easier and there has been a
renewed interest in SRM drives. In different
industries, wide range of speed control with fast
torque response regardless of load variation is
required. This can be achieved very efficiently for
SRM (
Miller, 2004). SRM exhibits certain advantages
like simple structure, high speed operation, wide
range of speed control, robustness, high torque per
volume, low rotor inertia, highly fault tolerant
structure etc. but despite of all these advantages one
incipient disadvantage makes this motor inefficient
for industrial application. This is due to the high
torque ripple that exists in the SRM characteristics.
In case of other industrial motors the torque ripple
can be minimised by profiling the motor driving
current. This profiling is done by proper design of
the PI (proportional-Integral) controller. The driving
current is forced to follow the reference current
either by Pulse Width Modulation (PWM) controller
or Hysteresis Controller. In case of SRM current
profiling is not the only solution.
The problem with SRM is due to its higher
degree of nonlinearity in the characteristics
compared to conventional industrial induction motor
or DC motor. It exhibits high torque as well as speed
ripple due to the typical torque characteristics. This
characteristics is due to nonlinear inductance profile
with respect to position and torque is dependent not
only on current but also on inductance profile.
Hence proper design of the controller for SRM
drives is itself an optimisation task.
In this present work a novel optimal design of the
controller for SRM drives has been proposed. Here
the tuning of the controller parameters and also the
position of current firing for every particular phase
are required. Hence the optimisation problem lies for
current shaping so that torque ripple is minimised.
This problem of nonlinearity in its characteristics
and torque ripple increases in case of variable speed
applications. To find out the optimum parameters of
the controller to obtain a good closed loop response
at different operating conditions is a hard task. The
PI controller parameters can be optimized by
conventional tuning methods, such as Ziegler-
Nicholson (ZN) method. Other tuning methods like
pole placement optimization technique are also done
391
Mukherjee J. and Chowdhuri S..
Multiobjective Optimisation by PSO for Switched Reluctance Motor (SRM) Drive.
DOI: 10.5220/0005101403910396
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 391-396
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

(George, 1994). Now-a-days Evolutionary methods
like Genetic Algorithm (GA), biologically inspired
methods like Particle Swarm Optimization (PSO),
Ant Colony optimisation (ACO) etc. are used for
tuning the parameters of the controllers. These new
tuning techniques can efficiently solve complex
problems like nonlinearity in the plant, variable
speed problems, where the conventional methods
may not optimize the controller parameter so
accurately. PSO is another Heuristic approach
which is inspired by the ability of flock of birds or
herd of animals to adapt to their environment. It was
developed in 1995 by James Kennedy and Russ
Eberhart while attempting to simulate the
choreographed, graceful motion of the swarm of
birds as a part of socio-cognitive study investigating
the motion of collective intelligence in biological
population. In PSO, a set of randomly generated
solutions propagates in the designed space towards
the optimal solution over a number of iteration based
on large amount of information about the designed
space (Kennedy, 1995). Both GA and PSO are
similar in the sense that these two techniques are
population based heuristic search methods and they
approach for the optimal solution by updating
generations. Since these approaches are supposed to
find a solution to a given objective function but
employ different strategies and computation effort, it
is appropriate to compare their performance.
In citation (Hameyer, 2008) the authors perform
a multiobjective optimization in a SRM aiming both
to maximize the mitigation of the torque ripple and
to minimize the degradations of the starting and
mean torques. The technique was applied on the
optimization of some rotor geometrical parameters
with the aid of finite element simulations to evaluate
the approximation points for the Kriging model. In
(Owatchaiphong, 2009), a design methodology is
presented for sizing a SRM. The proposed method
combines the use of genetic and fuzzy algorithms
together to simplify the design method. In (Balaji,
2011) Particle Swarm Optimization (PSO) based
design optimization of SRM has been presented.
Here The SRM design is formulated as multi
objective constrained optimization problem. The
objective functions for obtaining desired design are
maximization of average torque and minimization of
torque ripple with stator and rotor pole arc as design
variables. But all these optimisation are aimed to
optimise motors’ structural design.
Many researchers have applied both GA and PSO in
different fields of engineering e.g. In (Panda, 2007),
the authors have compared GA with PSO for
designing a TCSC based controller for power system
stability improvement.
In this present work we have applied PSO to search
for the optimal PI controller parameters as well as
firing angle and commutation angle of SRM drive
The performance of this optimization techniques in
terms of convergence rate, error minimization and
time complexity is good.
2 MATERIALS AND METHODS
2.1 Switched Reluctance Motor
The Reluctance Motor is an electric motor in which
torque is produced by the tendency of its moveable
part to move to a position where the inductance of
the excited winding is maximized or reluctance of
the winding is minimum. This motor has field coils
as of a DC Motor field winding for its Stator and no
coils or magnets in the Rotor. The rotor is aligned
whenever the diametrically opposite stator poles are
excited. In a magnetic circuit the rotating parts
prefer to come in minimum reluctance (maximum
inductance) position at the instance of excitation.
When two rotor poles are aligned with two stator
poles, another set of rotor poles will be out of
alignment with respect to another set of stator poles.
Hence by switching stator currents in a sequence, the
rotor is rotated.
(,)
(,) (,)
di dL i
VRiLi it
dt dt
(1)
2
1(,)
.
2
e
N
dL i
Ti
dt
(2)
eL
d
TT J B
dt
(3)
The SRM can be modeled using the following
system equations [(1)-(3)], where V, T
e
, T
L
are
applied voltage, electromagnetic torque and load
torque respectively. R and L are the resistance and
inductance of the stator per phase winding. J and B
are inertia constant and damping constants of the
machine. i is the current through the winding and
is the speed of the machine.
(,)
L
i
is the Stator
Inductance, which depends upon the rotor position
(fig 1) and also current in stator winding is a
function of both position and time, it is non-linear
and thus a simple equivalent circuit of SRM is not
possible. The inductance profile is curved at the top;
which causes high Torque ripples, speed
oscillations, increased audible noise and fatigue of
the shaft.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
392
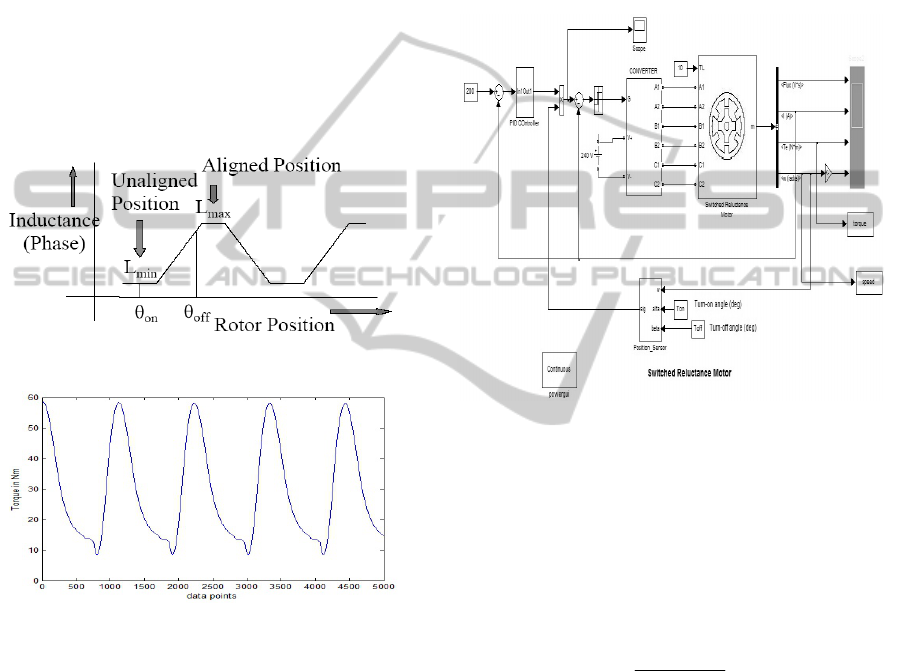
The currents are forced to each phase at an advance
angle
on
and commutated
at commutation angle
off
(Fig1)
.
Again depending upon the magnetic
saturation inductance varies for different current
level or it may be said that non linearity is
introduced both in current and inductance profile.
The magnitude of the current is dependent on load.
But the nonlinearity in inductance profile gives rise
to the torque ripple (Fig .2), as torque is a function
of both the current and the angular position. Hence
smooth control of speed and torque is problem area
for SRM drive. Controller can be designed to
mitigate these problems. In addition to this inherent
motor problem if the input voltage and frequency
fluctuates then this torque ripple problem is
aggregated.
Figure 1: Inductance profile vs. Rotor position.
Figure 2: Torque profile vs. Rotor position (as data
points).
2.2 Basic Plan of the Work
In this work, optimization of the parameters of PI
controller for current control and turn on and turn off
angle control of the controller of a SRM has been
done using PSO. The design has been considered for
a SRM (6/4 pole, 1 HP, 110V) in MATLAB
SIMULINK environment. This tuning has been done
to the model of SRM in offline. The gain parameters
for the current controller for a step input are initially
calculated by Ziegler-Nicholson’s optimization
technique which serves as the parent parameters for
current controller. From the design specification an
initial set for turn-on angle and turn off angle have
been randomly chosen within the permissible range.
For optimization, two different criteria for
smoothening of torque profile have been chosen
which serve as the fitness function of the algorithms.
The current applied to the machine has is
feedback control, which provides current reference
according to the error in torque.
The model of the test SRM is considered as the
Plant model (Fig 3). This model is nonlinear in
nature as the equation (1-3) and as described earlier.
Figure 3: Block diagram of the overall system.
In this wok the objective functions are
represented by eqn 4 and eqn 5. First objective is to
minimise the speed error by PI controller. Second
objective is to minimise of Total Torque Distortion
(TTD) by controlling the gain of the controller and
as well the turn on and turn off angle.
()
ref act
ei i i
(4)
max min
avg
TT
TTD
T
(5)
Where e(i) represents the error in current from
reference current to actual current.
TTD is the total n
phase torque distortion which is considered as the
fitness function.
TTD is calculated as the ratio
between the maximum and minimum torque
difference to average torque for a particular phase.
The output of the PI controller is described by
the following eqn 6 , where M
n
is the output of the
controller at n
th
instant which is derived from the (n-
1)
th
error and k
th
sum of previous errors. k
p
is the
proportional constant and k
i
is the integral constant.
The constrains of these multi objective problem are
eqn 7 and eqn 8.
MultiobjectiveOptimisationbyPSOforSwitchedReluctanceMotor(SRM)Drive
393

(1) ( )
np i
k
M
ken k en k
(6)
min max
min max
ppp
iii
kkk
kkk
(7)
max
ax
onmim on on
offmim off offm
TTT
TTT
(8)
The controller gains like proportional constants
(k
p
) and integral constant (k
i
) are limited by their
minimum and maximum limit beyond which the
controller will lose its stability.
For turn on (T
on
) angle and turn off (T
off
) angle
there are also minimum and maximum limit beyond
which per phase current control will not be
applicable.
2.3 Particle Swarm Optimisation
Particle Swarm Optimization (PSO) is a population
based stochastic optimization technique. It shares
many similarities with evolutionary computation
techniques such as genetic algorithm but the features
of PSO, like easy way of implementation, stable
convergence characteristics and computational
efficiency has made it much superior than others
(Mehdi, 2007 ), (Gaing, 2004) (Banerjee 2010). PSO
is initialized with a group of random particles
(solutions) and then searches for optima by updating
generations. In every iteration, each particle is
updated by following two “best” values. The first
one is the best solution (fitness) it has achieved so
far. (The fitness value is also stored.) This value is
called p
best
. Another “best” value that is tracked by
the particle swarm optimizer is the best value,
obtained so far by any particle in the population.
This best value is a global best and called
best
g
.
When a particle takes part of the population as its
topological neighbours, the best value is a local best
and is called
best
p
. After finding the two best
values, the particle update sits velocity and
positions.
1
2
1
*()*( )
*()*( )
11
id id
id id
id id
id id id
Vn Vn
c rand pbest n present n
c rand gbest n present n
present n present n V n
(9)
Where V
id
[n] is the particle velocity of the
current particle (n). p
best
[n] and g
best
[n] are defined
as state before. rand(n) is a random number between
(0,1). c1 and c2 are learning factors. The values of
c1 and c2 can be calculated as in eqn 10.
111 1
222 2
()*()
()*()
ter
fi i
axiter
ter
fi i
axiter
i
ccc c
m
i
ccc c
m
(10)
Where c
1i
, c
1f
, c
2i
and c
2f
are constants, iter is the
current iteration number and m
axiter
is the number of
maximum allowable iteration. The objective of such
modification is to boost up the global search over the
entire search space.
3 IMPLEMENTATION
In this section how the program has been
implemented in MATLAB is described.
3.1 Optimization of PI Controller using
Ziegler-Nichol’s Method
From all the methods designed to optimize PID
controller, Ziegler and Nichols’ method is mostly
used (Ogata, 2010). The methods are based on
characterization of process dynamics by a few
parameters and simple equations for the controller
parameters. The first method is applied to plants
with step responses. This type of response is typical
of a first order system with transportation delays.
The second method targets plants that can be
rendered unstable under proportional control. The
technique is designed to result in a closed loop
system with 25% overshoot. This is rarely achieved
as Ziegler and Nichols determined the adjustments
based on a specific plant model. Here the second
methods have been used, Kcr is the gain at critical
oscillation and Pcr is the time period. The controller
gains are specified in according to a rule (Table 1).
Table 1: PID Controller parameters.
PID Type Kp Ki Kd
P 0.5 Kcr Infinite 0
PI
0.45
Kcr
Pcr/1.2
PID 0.6 Kcr Pcr/2 Pcr/8
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
394
3.2 Optimisation of the Plant by PSO
Algorithm for PSO:
Initialise k
p
, k
i
values using
Z-N method
Initialisation of T
on
and T
off
for a particular range for
which the reluctance is
minimum and reluctance is
approaching maximum
Generate the initial k
p
,k
i
,T
on
and T
off
for a number of
population size in the
vicinity of the initial
values as real number.
Set generation =1
Simulate the SRM model by
setting the parameters of k
p
,
k
i
, T
on
and T
off
of the PI
controller for this set of
population size.
Calculate the error in torque
ripple for a particular
period of time for which the
current of that phase reaches
speed for each set of
population size for a
particular speed demand
While(!maximum iteration
number is achieved)
calculate fitness functions
Select the fittest individual
according to the fitness
function
Calculate p
best
of each
individual and g
best
of the
population
Update the velocity and
position of the best fitted
individual with pbest and
gbest
Increase the generation by
number 1
Compute k
p
, k
i
, T
on
and T
off
for the i
th
string
Simulate the plant with this
set of values
Evaluate fitness (i
th
) of the
simulation output
Perform selection mechanism to
generate sub-generation
Check the convergence
criteria.
4 RESUTS
Here a current demand is given. The problem is
started with a particular T
on
and T
off
angle and PI
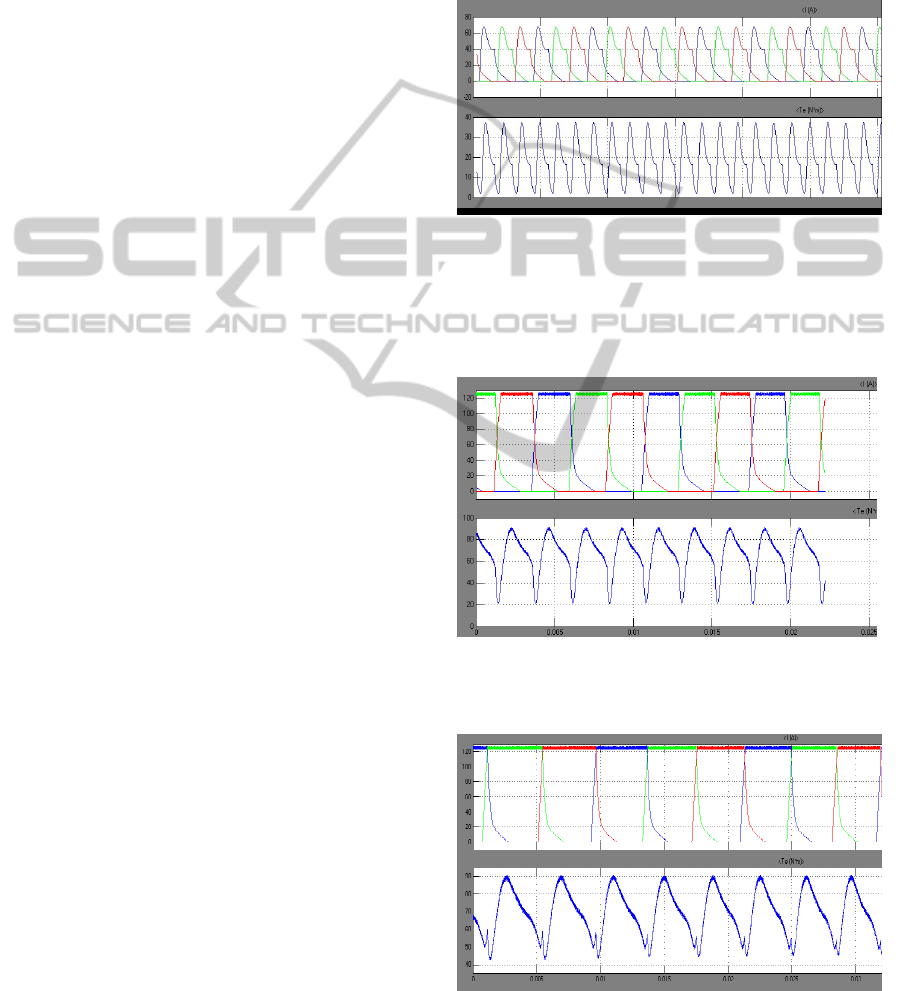
controller parameters. The current profile and torque
profile is shown in fig4 with this initial sets of
parameters.
Here TTD= 1.75
Figure 4: The current profile (upper) and the torque
developed (lower) before tuning the parameters.
After 20 iteration it has been found that the current
profile as well as the torque profile has been
improved (Fig 5).
Figure 5: The current profile (upper) and the torque
developed (lower) during tuning (after 20 iteration),
TTD=1.3.
Figure 6: The current profile (upper) and the torque
developed (lower) during tuning (after 50 iteration) with
TTD=0.78.
MultiobjectiveOptimisationbyPSOforSwitchedReluctanceMotor(SRM)Drive
395

After 50 iteration the torque profile has further been
improved. So far optimized value of the controller
coefficients are K
p
= 2.97, K
i
=1.23, T
on
=44.5
o
and
T
off
=77.6
o
obtained after 50 generations.
The present work provides immense research
possibilities for the future. This optimisation
problem is very much suitable since the SRM
exhibits very non linear characteristics. GA based
optimization will also be carried out and relative
comparison will be made between PSO and GA.
The stability considerations for controller design can
be augmented with the present scheme, which would
be regarded as a further constraint while computing
the fitness function. This work can be utilized to
solve optimization problems involving design of
controllers for more complex and non-linear
electromagnetic machines. This method as described
can be extended for SRM in online and time
complexity will be studied.
REFERENCES
T J E Miller, Electronic Control of Switched Reluctance
Machines, Newnes, Newnes ower Engineering
Series, 2004, ISBN 0 7506 50737.
Hameyer, Mitigation of the Torque Ripple of a Switched
Reluctance MotorThrough a Multiobjective
Optimization, IEEE Transactions on Magnetics, Vol.
44, No. 6, June 2008, pp 1018-1024.
Satit Owatchaiphong, Nisai H. Fuengwarodsakul, Multi-
Objective Based Optimization for Switched
Reluctance Machines Using Fuzzy and Genetic
Algorithms, IEEE conference Proceedings PEDS2009,
pp 1530-1532.
M. Balaji and Dr.V.Kamaraj, Design Optimization of
Switched Reluctance Machine using Particle Swarm
Optimization, International Conference on Electrical
Energy Systems (ICEES), 2011, pp164-169.
Kapsiotis,George., Tzafestas, Spyros., “PID self –tuning
control combining pole placement and parameter
optimization features (original research article)
Mathematics and Computers in Simulation”, Volume
37, Issues2-3,30 November1994, Pages133-142.
Eberhart,R., Kennedy,J., “Particle swarm optimization,” in
Proc. IEEE Int. Conf. Neural Networks, vol. IV, Perth,
Australia, 1995, pp. 1942–1948.
Panda, Sidhartha., Padhy, “Comparison of particle swarm
optimization and genetic algorithm for TCSC-based
controller design”, Department of Electrical
Engineering, Indian Institute of Technology, Roorkee,
Uttaranchal 247667, India, International journal of
Electrical and Electronics Engineering 1:5 2007.
Mehdi, Nasri., Hossein Nezamabadi-pour, and Malihe
Maghfoori, “A PSO Based Optimum Design of PID
Controller for a Linear Brushless DC Motor”, in
World Academy of Science, Engineering and
Technology 26 2007.
Gaing, Z.-L., “A particle swarm optimization approach for
optimum design of PID controller in AVR system,”
IEEE Trans. Energy Conversion, vol.19, pp. 384-391,
June 2004.
Banerjee, T., Choudhuri, S., Bera, J.N, Maity,A., “Off-line
optimization of PI and PID controller for a vector
controlled induction motor drive using PSO”,
(ICECE), 2010 International Conference on Electrical
and Computer Engineering, 18-20 Dec. 2010, On
Page(s): 74 – 77, ISBN: 978- 1-4244-6277-3.
Ogata, Katshuhiko, “Modern Control Engineering” (PHI
Learing Private Limited, Fifth edition,2010).
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
396
