Applicability of Thermal Comfort Models to Car Cabin Environments

Diana Hintea

, John Kemp

, James Brusey

, Elena Gaura

and Neil Beloe

Coventry University, Priory Lane, Coventry, CV1 5FB, U.K.

Jaguar Land Rover Ltd, Abbey Road, Whitley, Coventry, CV3 4LF, U.K.

Keywords:

PMV, Thermal Comfort Model, HVAC Control, Skin Temperature.

Abstract:

Car cabins are non-uniform and asymmetric environments in relation to both air velocity and temperature.

Estimating and controlling vehicle occupant thermal comfort is therefore a challenging task. This paper fo-

cuses on evaluating the suitability of four existing thermal comfort models, namely the Predicted Mean Vote

(PMV), Taniguchi’s model, Zhang’s model and Nilsson’s model in a variety of car cabin conditions. A series

of comfort trials were performed ranging from controlled indoor trials to on-road driving trials. The outputs

of all four models were compared to the sensation index reported by the subjects situated in the driver seat.

The results show that PMV and Nilsson’s model are generally applicable for the car cabin environment, but

that they are most accurate when there is a small air temperature rate of change (of under 1.5

◦

C per minute),

giving correlation levels of 0.91 and 0.93 for the two models respectively. Taniguchi’s and Zhang’s models

were found unsuitable for all conditions, with correlation levels ranging between 0.03 and 0.60. Nilsson’s

model is recommended by the authors based on the level of agreement with the subjective reports, its ability

to estimate both local and overall thermal sensation and the smaller number of input parameters.

1 INTRODUCTION

Car cabins are environments with inherent non-

uniformity and asymmetry in both air velocity and

temperature ﬁelds. Steady-state trends can be encoun-

tered for journeys in excess of 15-20 minutes, how-

ever 85% of journeys are of shorter duration (Cistern-

ino, 1999). Predicting passengers’ thermal comfort

for efﬁcient Heating, Ventilation and Air Condition-

ing (HVAC) control is therefore a complex problem.

More than forty years after its development,

Fanger’s Predicted Mean Vote (PMV) (Fanger, 1973)

remains the most used method for assessing occu-

pant thermal comfort in a range of environments.

Although designed speciﬁcally for use in buildings,

PMV continues to drive research into vehicle HVAC

control algorithms (Ueda and Taniguchi, 2000; Busl,

2011; Farzaneh and Tootoonchi, 2008). The main

reasons are the simplicity of measuring the air tem-

perature and humidity parameters, combined with the

ability to estimate the remaining parameters within

controlled tests. Nilsson (Nilsson, 2004) proposed

thermal comfort zones for 18 different body parts and

overall based on equivalent temperatures. Nilsson’s

model uses similar parameters with PMV (air temper-

ature, air ﬂow, mean radiant temperature and clothing

index). However, the model has the advantage of es-

timating local thermal sensation, as well as overall.

Skin temperature is shown to be a good predictor

of local and overall thermal sensation in the state of

art (Bogdan, 2011; Wang et al., 2007). Taniguchi’s

model (Taniguchi et al., 1992) was designed for ve-

hicular applications and is based on face skin tem-

perature only. Zhang’s thermal sensation and comfort

model (Zhang, 2003), on the other hand, is a more re-

cent model developed with transient, inhomogeneous

environments in mind. The model, however, has been

criticized in the literature for having too many coefﬁ-

cients, for the limitations of the experimentation and

for the body part set-point temperature approach (Luo

et al., 2007). Moreover, no validation of these two

skin temperature based models within daily driving

scenarios or other typical conditions encountered in

vehicular environments exists in the literature.

Considering the above, this paper evaluates PMV,

Taniguchi’s model, Zhang’s model and Nilsson’s

model on empirical data gathered in a variety of car

cabin conditions, establishing whether they are suit-

able for comfort-oriented vehicular control.

The main contributions of this paper are: 1) illus-

trating the range of conditions in which these mod-

els could be applied to drive comfort-oriented HVAC

control algorithms and 2) establishing which of the

four thermal comfort models is a better match of cabin

769

Hintea D., Kemp J., Brusey J., Gaura E. and Beloe N..

Applicability of Thermal Comfort Models to Car Cabin Environments.

DOI: 10.5220/0005101707690776

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 769-776

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

occupant thermal comfort in typical vehicular condi-

tions based on gathered empirical data.

The paper is structured as follows: Section 2

presents an overview of the the four thermal com-

fort models. Section 3 describes the data gathering

methodology, focusing on the instrumentation used,

the participating subjects and the range of conditions

encountered in the car cabin. Section 4 presents the

results obtained when comparing the sensation index

corresponding to the four models with the subjects’

reported sensation. Finally, Section 5 concludes the

paper.

2 BACKGROUND

Based on the review provided by Cheng et al. (Cheng

et al., 2012), the following thermal comfort models

were implemented and evaluated on the data gath-

ered: PMV, Taniguchi’s model, Nilsson’s model and

Zhang’s model. These thermal comfort models are re-

viewed in (Alahmer et al., 2011; Cheng et al., 2012;

Orosa, 2009) and discussed in the following subsec-

tions.

With regard to other models, Matsunaga et

al. (Matsunaga et al., 1993) adopted, for example, the

concept of Average Equivalent Temperature (AET) in

order to compute the PMV sensation index. The AET

is a surface area-weighted value for three body parts:

the head with a weight of 0.1, the abdomen with a

weight of 0.7 and the feet with a weight of 0.2. Be-

cause the end product is the PMV index, this tech-

nique is not evaluated in this paper. Also, the Berke-

ley advanced human thermal comfort model (Arens

et al., 2006) is used as a cabin occupant comfort es-

timator in multiple works. The virtual manikin in the

software model estimates occupant skin temperatures

and Zhang’s model uses the latter to calculate thermal

sensation and thermal comfort. As this paper is con-

cerned with empirical results rather than simulation,

only Zhang’s model is evaluated.

2.1 Predicted Mean Vote (PMV)

Fanger (Fanger, 1970) developed the PMV model

in 1967 based on thermo-regulation and heat bal-

ance theories. These theories are based on human

bodies employing physiological processes in order

to maintain a balance between the heat produced by

metabolism and the heat lost from the body. The PMV

index provides a score that corresponds to the Ameri-

can Society of Heating, Refrigerating and Air Condi-

tioning Engineers (ASHRAE) thermal sensation scale

shown in Table 1 and it is deﬁned as the average

Table 1: PMV thermal sensation index.

3 Hot

2 Warm

1 Slightly warm

0 Neutral

-1 Slightly cool

-2 Cool

-3 Cold

thermal sensation felt by a large group of people in

a space. The PMV model combines four physical

variables (air temperature, air velocity, mean radiant

temperature and relative humidity) and two personal

variables (clothing insulation and activity level). The

mathematical equations used to derive the PMV index

are given in the ISO 7730 standard (ISO, 2005).

Fanger validated and reﬁned the comfort equation

with data from other previous thermal comfort studies

combined with his own, summing to approximately

1400 participants. Fanger stated that the PMV model

should be used with care for indexes below −2 and

above +2 and that signiﬁcant errors can appear in hot

environments. PMV’s main advantages are the stan-

dardisation of the implementation and that if some of

the constituent parameters cannot be measured, they

can be approximated without introducing a signiﬁcant

error in the outputted PMV index.

However, PMV was never intended to be

applied in transient, inhomogeneous conditions.

Van Hoof (van Hoof, 2008) discussed PMV’s applica-

bility to transient conditions, concluding that there is

a lack of PMV assessment in transient environments

and that extensive research is still required. Also,

body parts experience local discomfort and thermal

sensation levels differ from each other and from the

overall sensation (Arens et al., 2006; Nakamura et al.,

2008). With the introduction of heated/cooled seats

and steering wheels the impact on individual body

part sensation is even higher. Therefore, a big disad-

vantage of the PMV model is that it is unable to dif-

ferentiate between sensations at different body parts,

which is an important capability in the case of vehic-

ular HVAC control systems.

2.2 Taniguchi’s Model

Skin temperature is shown to be a good predictor of

local and overall thermal sensation in the state of art

(Bogdan, 2011; Wang et al., 2007), especially in case

of extremities such as face and hands. Taniguchi et

al. (Taniguchi et al., 1992) developed a multiple linear

regression model relating the average facial skin tem-

perature and its rate of change to the Overall Thermal

Sensation (OTS) in a vehicle environment. The model

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

770

was proposed based on a series of human subject tests

and OTS is calculated as:

OTS = 0.81 (T

− 33.9) + 39.1

where T

is the face skin temperature and

is the

face skin temperature rate of change.

A signiﬁcant disadvantage of this model is not tak-

ing into account that the thermal sensation of body

segments other than the face also impact the overall

body thermal sensation. Moreover, it does not allow

the computation of local thermal sensation.

2.3 Zhang’s Model

Zhang (Zhang, 2003) developed local and over-

all thermal sensation and comfort models tar-

geted at transient, non-uniform conditions. Unlike

Taniguchi’s model, Zhang’s models are based on skin

temperatures at multiple sites along with core temper-

ature, if available. A nine point analogue scale (shown

in Table 2) is used for expressing thermal sensation.

Experimental tests were carried out at UC Berkeley,

with subjects placed into chambers of uniform tem-

perature and with heated or cooled air applied indi-

vidually to 19 separate body areas. The tests were

carried out in a climate-controlled chamber, consist-

ing of both cold and hot test cases. Throughout these

tests, subjects were allowed to adjust the HVAC set-

tings to their preference. Skin temperature was mea-

sured at 19 locations using thermocouples, while core

temperature was measured using an ingestible tem-

perature device. Local and overall sensation equa-

tions were developed, using the measured skin tem-

perature, mean skin temperature and core tempera-

ture along with subjective reports. Zhang validated

the model against subjective reports and acceptable

results were obtained. The coefﬁcient of determina-

tion (R

) for the overall sensation model was 0.95 and

the standard deviation of residuals was 0.54.

Luo et al. (Luo et al., 2007) criticize the model,

citing that “the mathematical model is not practicable

as it is limited by having too many coefﬁcients, and

because of the experiment’s limitation, the regression

analysis result cannot be assured either”. Further-

more, they criticize the body part set-point tempera-

ture approach of the model. Also, Cheng et al. (Cheng

et al., 2012) points out that during the experiments,

they focused more on cooling local body parts in

warm environments than on warming local body parts

in cool environments. In addition, the inﬂuence of lo-

cal stimulation duration and intensity were not var-

ied in the test. Moreover, no validation of the model

Table 2: Zhang’s thermal sensation scale.

4 Very Hot

3 Hot

2 Warm

1 Slightly Warm

0 Neutral

-1 Slightly Cool

-2 Cool

-3 Cold

-4 Very Cold

within daily driving scenarios or other typical condi-

tions encountered in vehicular environments exists in

the literature. The main advantage of Zhang’s model

over PMV is its ability to determine local sensation

indexes.

2.4 Nilsson’s Model

Nilsson (Nilsson, 2004) proposed clothing indepen-

dent thermal comfort zones for 18 different body parts

based on equivalent temperatures. Equivalent temper-

ature is formally deﬁned as the uniform temperature

of an imaginary enclosure with air velocity equal to

zero in which a person will exchange the same dry

heat by radiation and convection as in the actual non-

uniform environment (Nilsson and Holmer, 2002).

Equivalent temperature can be computed based on en-

vironmental parameters such as air temperature, mean

radiant temperature, air ﬂow and clothing index or

it can be directly measured with appropriate instru-

ments (Nilsson and Holmer, 2002). Once the equiv-

alent temperature is calculated, the local or overall

thermal sensation level can be estimated using the di-

agrams in Figure 1. Nilsson developed this model

through experimentation with approximately 500 sub-

jects.

A gap in the literature that this paper responds to

is the lack of empirical evaluation of the thermal com-

fort models presented within vehicular environments

in order to establish whether any of them is suitable

for comfort-oriented HVAC control. According to the

authors’ knowledge, no empirical data based evalua-

tion of these models in vehicular environments exists

in the state of art.

3 METHODOLOGY

In order to address this lack of empirical evaluation,

car cabin data and subjective comfort readings were

gathered over a wide range of experimental condi-

tions. This section provides a description of the par-

ApplicabilityofThermalComfortModelstoCarCabinEnvironments

771

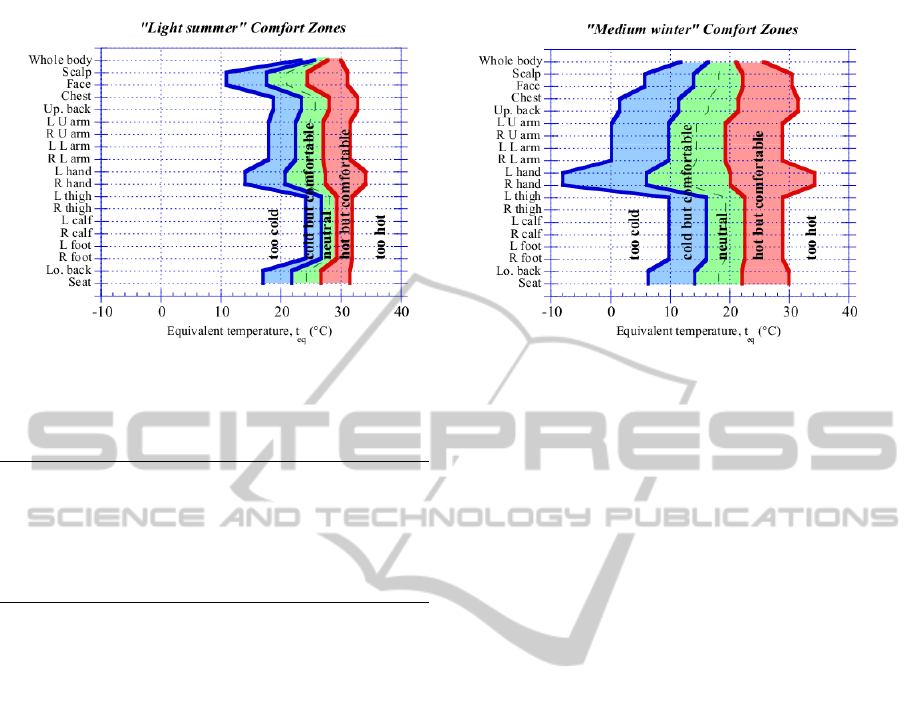
Figure 1: Nilsson’s clothing independent thermal sensation diagrams (Nilsson, 2004).

Table 3: Subject details.

Subject Gender Age Height (cm) Weight (kg)

1 Male 46 173 78

2 Female 37 157 73

3 Male 56 166 70

4 Male 49 178 75

5 Female 24 162 48

6 Male 26 176 77

7 Female 34 160 55

ticipating subjects in the comfort trials, the instrumen-

tation used and the variety of conditions encountered

throughout the trials.

3.1 Participating Subjects

Seven adults (four males and three females) were se-

lected as experimental subjects. Their ages were be-

tween 24 and 56 years old, with heights between

1.57 cm and 1.78 cm and weights between 48 kg and

78 kg, as presented in Table 3. The subjects occu-

pied the driver seat and were asked by the observer

in the right-hand rear passenger seat for their overall

thermal sensation throughout the experimental trials

(as detailed in Section 3.3). The thermal sensation

scale used was the ASHRAE seven point scale (coin-

cides with the PMV scale) shown in Table 1. Cloth-

ing was standardised across all trials and subjects,

consisting of long trousers and a short-sleeved, light-

coloured shirt or blouse, corresponding to a clothing

index value of 0.7.

3.2 Measured Variables

Throughout all trials, equivalent temperature was

monitored at eight locations (corresponding to head,

chest, left lower arm, right lower arm, left upper arm,

right upper arm, thigh and calf) using the INNOVA

Flatman support manikin, shown in Figure 2 (right)

and the associated INNOVA 1221 thermal comfort

data-logger. Throughout the trials, the Flatman was

positioned in the front passenger seat, continuously

calculating equivalent temperature via the dry heat

loss sensors and computing the PMV thermal sensa-

tion level. Cabin air and surface temperature data was

gathered from 19 points using type K thermocouples

and was recorded by a Grant Instruments DataTaker

DT85 data logger. Near-body air temperature and rel-

ative humidity were measured at eight points (close

to the neck, wrist, chest, thigh and calf locations)

using type T thermocouples and Honeywell S&C

HIH-5031 humidity sensors and also recorded by a

SQ2040 data-logger. Solar loading at the driver sun-

roof location was measured using automotive solar

sensors and recorded by a Grant Instruments Squirrel

SQ2040 data-logger. The driver’s center and outboard

face vent air temperatures were monitored using type

K thermocouples and recorded by the SQ2040 data-

logger. Finally, subject skin temperature was also

monitored at eight points (neck, left and right wrist,

chest, left and right thigh and left and right calf) using

Grant Instruments EUS-UU-VL2-0 thermistors and

recorded by the SQ2040 data-logger.

3.3 Experimental Procedure

The trials were performed from the 8

to the 29

August 2011. The test car used was a Jaguar XJ (2010

model year). Three types of trials were performed,

with 78 trials in total, as described in the following

sections.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

772

Figure 2: Experimental data gathering. Left: Mean radi-

ant temperature sensor. Right: Upper body of the Flatman

thermal manikin.

3.3.1 Variable Cabin Temperatures Within

Steady State External Conditions (T1)

These trials were performed within an enclosed space

in order to eliminate wind and precipitation effects.

Both the subjects and the test car were preconditioned

for 20 minutes to 22

◦

C. At the outset of the experi-

ment the subject, occupying the driver seat, remained

in static conditions for 10 minutes. The temperature

was then increased by 1

◦

C every 3 minutes until it

reached 28

◦

C. The subject then left the car, which

was again conditioned to 22

◦

C. After the subject re-

turned, they again remained in static conditions for 10

minutes. Then the temperature was decreased by 1

◦

every 3 minutes until it reached 16

◦

C. The air ﬂow

from the HVAC system was set to high or medium

settings. During the static conditions, the subject re-

ported thermal sensation and comfort at the 5, 7, and

9 minute marks and one minute before each tempera-

ture change when the HVAC set point was varied.

These trials are characterized by the following

conditions: 1) absolute average car cabin temperature

rates of change peaking at around 1.5

◦

C per minute,

but usually under 1

◦

C per minute; 2) precondition-

ing of the cabin and subject at the same temperature;

3) no precipitation or wind effects; 4) steady ambient

temperature (between 19

◦

C and 24

◦

C ) varying by

less than 1

◦

C within an individual trial.

3.3.2 User Control with Steady State External

Conditions (T2)

These trials were performed within an enclosed space.

The car and the subjects were preconditioned to a neu-

tral (22

◦

C), hot (28

◦

C), or cold (16

◦

C) tempera-

ture. The subjects entered the car and remained inside

for 15 minutes time, during which they were permit-

ted to adjust the air conditioning at will in order to

make themselves more comfortable. The control ad-

justments they made were logged in addition to the

previously described parameters. Thermal comfort

and sensation was reported every two minutes, with

the ﬁrst report being at the start of the test.

These trials are characterized by the following

conditions: 1) absolute average car cabin temperature

rates of change peaking at 8

◦

C per minute; 2) precon-

ditioning of the cabin and subject at the same temper-

ature; 3) no precipitation or wind effects; 4) steady

outside temperature (between 17

◦

C and 25

◦

C) vary-

ing by less than 1

◦

C within an individual trial.

3.3.3 User Control in Driving Conditions (T3)

These trials are similar to the previous ones (T2), ex-

cept that the subjects drove the car on private roads

and there was no additional solar loading applied be-

yond that naturally falling on the car. Drivers were

required to turn and change speed at frequent inter-

vals in order to simulate to an extent the daily driv-

ing routine. This provided a comparison against the

baseline established in the previous type of trials, as

it was expected that the acceptable temperature range

would widen as the driver was required to concen-

trate on driving. Thermal comfort and sensation was

reported every two minutes, with the ﬁrst report being

at the start of the test.

These trials are characterized by the following

conditions: 1) absolute average car cabin temperature

rates of change peaking at 10

◦

C per minute; 2) pre-

conditioning of the cabin and subject at the same tem-

perature; 3) ambient solar load and wind; 4) ambient

outside temperature (between 12

◦

C and 28

◦

C) vary-

ing by less than 2

◦

C within an individual trial.

The ﬁrst set of trials were aimed at determining

the extents of passenger thermal comfort with no ex-

treme conditions, while the second set offered infor-

mation on what control adjustments were required

in order for the cabin occupants to feel comfortable

and how quickly thermal neutrality was reached. The

third set of trials aimed to capture the comfort ranges

during daily driving and therefore with the subject

less focused on their comfort. Altogether, the mul-

titude of conditions (solar load, stationary or driving,

different blower speeds, different initial temperatures)

allowed a thorough evaluation of the validity of the

selected thermal comfort models. Table 4 provides a

summary of the trials performed.

Throughout the three sets of trials, the Flatman

was positioned in the front passenger seat, with the

subject occupying the driver seat. In order to ensure a

valid comparison between the thermal sensation com-

puted/reported by the two sides the following were

ensured: 1) the front passenger vent and driver vent

had the same orientation and delivered the same set-

point temperature; 2) both the test car (with the Flat-

man inside) and the driver were preconditioned to the

same temperature prior to each trial.

ApplicabilityofThermalComfortModelstoCarCabinEnvironments

773

Table 4: Summary of the experimental conditions in all trials.

Trial Duration (mins) Blower speed Solar load Driving Pre-conditioning Subjects

T1 56 High or Medium Controlled No 22

◦

C 7

T2 15 User Controlled No 16

◦

C, 22

◦

C or 28

◦

C 7

T3 15 User Ambient Yes 16

◦

C, 22

◦

C or 28

◦

C 6

4 RESULTS

This section provides an evaluation of the four ther-

mal comfort models based on the gathered data de-

scribed in Section 3. The purpose is to establish

whether they can accurately predict car cabin occu-

pant thermal sensation in any of the conditions in or-

der to be used for comfort based HVAC control. For

this purpose the overall thermal sensation reports of

the drivers were compared to i) the PMV index as

computed by the Flatman, ii) Zhang’s index computed

from the measured skin temperatures, iii) Taniguchi’s

index computed from the measured facial skin tem-

perature and iv) Nilsson’s index computed from the

measured average body equivalent temperature.

PMV is widely used for car cabin comfort

based HVAC controllers (Busl, 2011; Farzaneh and

Tootoonchi, 2008). The reason is the simplicity of

estimating the PMV index. However, does PMV ac-

tually reﬂect the reported sensation levels of the occu-

pants? Table 5 presents the correlation coefﬁcient and

the determination coefﬁcient R

between the subjec-

tive and experimental data for all models. The corre-

lation coefﬁcient quantiﬁes the degree of correlation

between two variables, while the R

coefﬁcient indi-

cates how well data points ﬁt the linear regression.

The p-value for a regression gives the probability that

the result is not derived by chance. For all results pre-

sented, the p-value is smaller than the threshold (p ¡

0.001) and the results are therefore signiﬁcant.

In the case of PMV, the highest level of agree-

ment corresponds to trials T1, with a correlation index

of 0.91. The high correlation is somewhat expected

due to the stable conditions encountered throughout

trials T1 (interior temperature rates of change less

than 1.5

◦

C per minute, stable outside temperature

and no wind or precipitation). The experimental data

matches less accurately the subjective reports in trials

T2 and T3. The correlation index between the two is

0.76 for T2 and 0.78 for T3. Overall Flatman’s PMV

tended towards colder reports than the subjective re-

ports. For example, for T1, drivers reported thermal

sensations of up to 4 (corresponding to “very hot”),

whereas Flatman’s PMV did not go beyond 3 (corre-

sponding to “hot”).

The results indicate that PMV can be applied in

vehicle cabins to infer passenger comfort within a

limited set of conditions, however the model brings

forward another important issue in this type of envi-

ronment, the inability to differentiate between differ-

ent parts of the body. Due to the non-uniform nature

of the environment, the difference in thermal sensa-

tion over small distances is considerable and so effec-

tive HVAC control should be able to warm up or cool

down separately different body parts.

With PMV’s accuracy limited to a narrow range of

conditions, the authors further investigated two skin

temperature based models: Taniguchi’s model and

Zhang’s model. For Taniguchi’s model, as Table 5

illustrates, the highest level of agreement corresponds

to trials T1, with a correlation index of 0.56, while

in trials T2 and T3 the match is poor, with correla-

tion indexes of 0.03 and 0.15, respectively. Face skin

temperature seems to have a higher impact on over-

all thermal sensation when the rate of change of air

temperature is low (less than 1.5

◦

C per minute), as

suggested by the higher correlation for trials T1. As

Taniguchi’s model was developed only with respect

to facial skin temperature, it is further interesting to

see if Zhang’s model improves on this by taking into

consideration 8 different body parts.

Zhang’s model was developed, like Taniguchi’s,

for transient environments such as car cabins. Dur-

ing experimentation, skin temperature was sampled

at only 8 sites, compared to the 19 sites speciﬁed by

Zhang. This is justiﬁed by the fact that within real-

time vehicular comfort control, it would be infeasible

to monitor skin temperature at all locations speciﬁed

by Zhang. However, in order to ensure that the sum

of skin temperature segment weights is 1, the weights

for the contribution of local thermal sensations to the

overall sensation were normalised. Mean skin tem-

perature was calculated as a proxy for core tempera-

ture (this approach being suggested by Zhang). The

body part skin temperatures recorded at the beginning

of each trial were used as the set point temperatures

of the body segments in the model. As table 5 shows,

the correlation levels are poor: 0.10 for T1, 0.50 for

T2 and 0.60 for T3. As it stands, for trials T1, facial

skin temperature alone proved to be a better estimator

than the combination of 8 different body parts. The

performance of the two skin temperature based mod-

els does not appear to be sufﬁcient to support vehicu-

lar HVAC comfort control.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

774

Table 5: Statistic metrics between the models’ thermal sensation index and the reported sensation.

PMV Taniguchi Zhang Nilsson

Type Correlation R

Correlation R

T1 0.91 0.85 0.56 0.32 0.10 0.0001 0.93 0.86

T2 0.76 0.57 0.03 0.001 0.50 0.25 0.77 0.59

T3 0.78 0.61 0.15 0.02 0.60 0.35 0.79 0.62

In order to compute the overall thermal sensation

index of Nilsson’s model, the equivalent temperature

at 8 different body parts was averaged based on body

area weights. Once the average equivalent temper-

ature is computed, the overall thermal sensation in-

dex can be found from Figure 1, using the diagram

corresponding to light clothing (the participants wore

light clothing throughout the experiments). Nilsson’s

model had a similar performance to the PMV model.

The highest level of agreement with the subjective re-

ports corresponds to trials T1, with a correlation index

of 0.93. For trials T2 and T3, the correlation index

is lower, of 0.77 and 0.79, respectively. The simi-

lar performance is somewhat expected, because Flat-

man’s PMV index is also based on the measured aver-

age equivalent temperature. The advantage Nilsson’s

model has over PMV is that local thermal sensation

can also be computed and used for control.

5 CONCLUSIONS AND

DISCUSSION

In this paper we evaluated the applicability of four

thermal comfort models, namely PMV, Taniguchi’s

model, Zhang’s model and Nilsson’s model in a range

of conditions speciﬁc to cars. A ﬁrst step towards this

aim was to design experimental trials covering a wide

range of conditions: with preconditioning of the oc-

cupants and cabin at different temperatures, with or

without ambient solar load, wind and precipitations,

with steady or varying outside ambient temperature

and with different temperature rates of change within

the cabin.

Based on the experimentally gathered data, the

PMV index and Nilsson’s index accurately matched

(with correlations of 0.91 and 0.93, respectively) the

occupant reported thermal sensation within a limited

set of conditions: preconditioning of the passenger

and the cabin at the same temperature, a steady out-

side temperature and low rates of change of the in-

terior temperature (lower than 1.5

◦

C per minute).

Higher interior temperature rates of change (up to

◦

C per minute), ambient solar load and wind leads

to lower correlation factors, between 0.76 and 0.79.

The overall sensation computed using the two

skin temperature based thermal comfort models

(Taniguchi’s model and Zhang’s model) poorly

matched the subjective reports throughout all trial

types (correlations between 0.10 and 0.60). Overall,

the two skin temperature based models appear to have

little success and their accuracy is not sufﬁcient to

support vehicular HVAC comfort control.

Capitalizing on our ﬁndings, Nilsson’s model is

recommended by the authors in preference to the

other three models for vehicular comfort oriented

control. The model provided similar results to PMV.

However, an important advantage Nilsson’s model

has over PMV is its ability to estimate local ther-

mal sensation, which the authors see as an impor-

tant capability for the new generation of vehicular

HVAC control systems. Moreover, Nilsson’s model

only requires two input parameters—equivalent tem-

perature and clothing index—rather than six parame-

ters in PMV’s case, some of which could not feasibly

be determined by an automated system.

The deviation between the Flatman’s PMV out-

put and the subjective responses may be because the

subjects were in contact with the seat and the steer-

ing wheel whereas the Flatman’s dry heat loss sen-

sors were not. This could be conﬁrmed via further

experimentation. Another related avenue for future

work is in regard to heated/cooled seats and steering

wheels. These are becoming more widespread and

will clearly have an impact on thermal sensation and

comfort, which should be evaluated through empirical

work.

It is known that no thermal comfort model can

provide a perfect match for what people feel. The

description of PMV, for example, acknowledges that

any given environment will leave at least 5% of peo-

ple dissatisﬁed. One reason is the subjective nature of

thermal sensation and comfort in terms of how they

are felt and, also, how they are reported. However,

adopting Nilsson’s model as a basis for estimating oc-

cupant comfort control and further integrating online

learning within the car for tuning individual prefer-

ences would lead to a more thermally comfortable ve-

hicular environment.

ApplicabilityofThermalComfortModelstoCarCabinEnvironments

775

ACKNOWLEDGEMENTS

The Low Carbon Vehicle Technology Project

(LCVTP) was a collaborative research project be-

tween leading automotive companies and research

partners, revolutionising the way vehicles are pow-

ered and manufactured. The project partners included

Jaguar Land Rover, Tata Motors European Techni-

cal Centre, Ricardo, MIRA LTD., Zytek, WMG and

Coventry University. The project included 15 au-

tomotive technology development work-streams that

will deliver technological and socio-economic out-

puts that will beneﬁt the West Midlands Region. The

19 million project was funded by Advantage West

Midlands (AWM) and the European Regional Devel-

opment Fund (ERDF).

The authors would like to thank the anonymous

reviewers for their insightful comments.

REFERENCES

Alahmer, A., Mayyas, A., Mayyas, A., Omar, M., and

Shan, D. (2011). Vehicular thermal comfort models; a

comprehensive review. Applied Thermal Engineering,

31:995–1002.

Arens, E., Zhang, H., and Huizenga, C. (2006). Partial

and whole-body thermal sensation and comfort, part

ii: Non-uniform environmental conditio. Journal of

Thermal Biology, 31:60–66.

Bogdan, A. (2011). Case study assessment of local and gen-

eral thermal comfort by means of local skin temper-

ature. International Journal of Ventilation, 10:291–

300.

Busl, M. (2011). Design of an energy-efﬁcient climate con-

trol algorithm for electric cars. Master’s thesis, Lund

University.

Cheng, Y., Niu, J., and Gao, N. (2012). Thermal comfort

models: A review and numerical investigation. Build-

ing and Environment, 47:13–22.

Cisternino, M. (1999). Thermal climate in cabs and mea-

surement problems. In CABCLI Consortium.

Fanger, P. (1970). Thermal Comfort. Danish Technical

Press.

Fanger, P. (1973). Assessment of man’s thermal comfort

in practice. British Journal of Industrial Medicine,

30:313–324.

Farzaneh, Y. and Tootoonchi, A. (2008). Controlling au-

tomobile thermal comfort using optimized fuzzy con-

troller. Applied Thermal Engineering, 28:1906–1917.

ISO (2005). Ergonomics of the Thermal Environment.

Luo, X., Hou, W., Li, Y., and Wang, Z. (2007). A fuzzy

neural network model for predicting clothing thermal

comfort. Computers and Mathematics with Applica-

tions, 53:1840–1846.

Matsunaga, K., Sudo, F., Tanabe, S., and Madsen, T. (1993).

Evaluation and measurement of thermal comfort in the

vehicles with a new thermal manikin. Technical re-

port, SAE Paper.

Nakamura, M., Yoda, T., Crawshaw, L., Yasuhara, S., Saito,

Y., Kasuga, M., Nagashima, K., and Kanosue, K.

(2008). Regional differences in temperature sensation

and thermal comfort in humans. Journal of Applied

Physiology, 105:1897–1906.

Nilsson, H. (2004). Comfort Climate Evaluation with Ther-

mal Manikin Methods and Computer Simulation Mod-

els. PhD thesis, Royal Institute of Technology.

Nilsson, H. and Holmer, I. (2002). Deﬁnitions and mea-

surements of equivalent temperature. Technical re-

port, The Climate Group, National Institute for Work-

ing Life, Solna, Sweden.

Orosa, J. (2009). Research on general thermal comfort mod-

els. European Journal of Scientiﬁc Research, 2:217–

227.

Taniguchi, Y., Hiroshi, A., and Kenji, F. (1992). Study

on car air conditioning system controlled by car oc-

cupants’ skin temperatures - part 1: research on a

method of quantitative evaluation of car occupants.

Technical report, SAE Paper.

Ueda, M. and Taniguchi, Y. (2000). The prediction of the

passenger’s thermal sensation level using a neural net-

work and its application to the automobile hvac con-

trol.

van Hoof, J. (2008). Forty years of fanger’s model of ther-

mal comfort:l comfort for all? Indoor Air Journal,

18:182–201.

Wang, D., Zhang, H., Arens, E., and Huizenga, C. (2007).

Observations of upper-extremity skin temperature and

corresponding overall-body thermal sensations and

comfort. Building and Environment, 42:3933–3943.

Zhang, H. (2003). Human Thermal Sensation and Comfort

in Transient and Non-Uniform Thermal Environments.

PhD thesis, University of California, Berkeley.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

776