
Parallel Simulation of Dynamic Communication Processes on the Base
of Probability Time Automata
Henryk Piech
1
, Grzegorz Grodzki
1
and Aleksandra Ptak
2
1
Institute of Computers and Information Sciences, Czestochowa University of Technology,
Dabrowskiego 73, Czestochowa, Poland
2
Department of Applied Informatics, Czestochowa University of Technology, Czestochowa, Poland
Keywords:
Parallel Conversion, Communication Security, Probability Time Automata.
Abstract:
The proposition is connected with the research of the security or threatens referring to message decryption,
user dishonesty, non-fresh nonce, uncontrolled information jurisdiction, etc. (security attributes), in network
communication processes. Encrypted messages are usually sent in the form of protocol operations. Protocols
may be mutually interleaving, creating the so called runs, and their operations can appear as mutual parallel
processes. The investigation regards both particular security attributes and their compositions referring to more
general factors, such as: concrete users, protocols, public keys, secrets, messages, etc. The abovementioned
situation forms a conception about parallel strategy realized with the help of PTA and Petri net that includes
the set of security tokens (attributes) in each node.
1 INTRODUCTION
The set of security communication attributes is pre-
sented in (Burrows et al., 1990). These elements are
logically combined in the form of rules. The BAM
and Hoare logic are used. The rules have a traditional
form ”if conditions then conclusions ”. Conditions
are represented by protocol actions, whereas conclu-
sions by attributes. Attribute corrections (modifica-
tions) are realized according to rules. It is necessary
to regard the fact that the same attributes have a timed
character, i.e. they lose their secure values in the acti-
vation time (Kwiatkowska et al., 2002). The proposed
convention, in the second section, permits to change
the activation time distance into probability values
equivalent to a security level. The distributed form
of investigation, according to chosen security factors,
suggests using the parallel composition of the PTA
node structure (Szpyrka and Szmuc, 2006). In gen-
eral, calculation process organization is presented in
the section devoted to the thread creation and the dy-
namic of their new designation (Tadeusiewicz, 2011).
The acceleration estimators, according to several vari-
ants of the security analysis parallelization, are pro-
posed in section 3. The selection and adaptation of
the PTA and Petri net structure is presented in a gen-
eral form in the last section.
2 DESCRIPTION OF SECURITY
STATE WITH HELP OF
PROBABILITY - TIME
AUTOMATON NODES
The security state is assigned to communication run
factors, such as: user, message, protocol, key, nonce,
secret, etc. Generally, a communication run con-
sists of interleaving protocols. Protocol is created
as a sequence of operations built on the basis of
users (sender, receiver, intruder), shared keys, nonces,
secrets. The structure and operation (action) com-
ponents are arguments exploited by rules (Burrows
et al., 1990) to extend the set of security parameters.
Same of such kind of parameters are included directly
in protocol operations.
set sec1 = sp ⊆ OP,
set sec2 = r(sp ⊆ OP),
set sec = set sec1 ∪ set sec2,
where:
set sec1 - security parameters included in protocols
operations,
set
sec2 - security parameters inferred from logic
rules,
sp - security parameters,
r = {r
1
,r
2
,..., r
k
} - the set of rules,
237
Piech H., Grodzki G. and Ptak A..
Parallel Simulation of Dynamic Communication Processes on the Base of Probability Time Automata.
DOI: 10.5220/0005102702370242
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),
pages 237-242
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

OP = {Op
1
,Op
2
,..., Op
m
} = {op
1,1
,op
1,2
,...,
...,op
m,l(m)
} - the set of protocol operations,
set sec - the full set of security parameters,
Op(i) - set of operations in protocol i,
k - rule number,
m - protocols number,
l( j) - protocol j operation number.
Figure 1: PTA node presentation - example of probability
(left) and binary (right) form.
The task of a user consists in the selection of the
set of security attributes, which will be the compo-
nents of nodes of probability - time automaton (PTA).
Components can be evaluated in two ways: as real
and binary values. Real values express the probabil-
ity of security parameters and binary values express
the acceptable level of parameters. Therefore, it was
decided to introduce a notation of tokens which will
be adequate to node security components in the binary
form.
Elements in frames mean selected security at-
tributes. Arrows appoint security threshold levels of
attributes. If component probability, represented by
the white bar, is greater than security threshold then
security token is acceptable, which is represented by
the white ring in the right part of the figure. The
example structure of the security node is presented
in Fig. 2. Security attribute types infer from proto-
col logic (BAN, Hoare or PCL) formalisms (Burrows
et al., 1990) which is partly described, by character of
communication dealings, in the following way:
A ↔
K
B - users A, B communicate via shared key K,
→
K
A - user A has K as its public key,
A ⇔
Y
B - users A and B share Y as a secret,
{X}
K
- the message X encrypted by key K,
{X}
A
K
- the message X encrypted by key K by user A,
< X >
Y
- the message X with a secret Y attached,
Figure 2: The structure of security node consisting of six
attributes - example.
A| ≡ X - user A believes the message X,
A X - user A sees the message X,
A X - user A once send the message X,
A| ⇒ X - user A has jurisdiction over X,
#(X) - the message is fresh.
At this point, we can to cite (Burrows et al., 1990)
several rules from the logic of authentication proto-
cols (BAN):
1. Authentication rule - Type I :
if (A| ≡ ((A ↔
K
B), A X
K
) then (A| ≡ (B X).
The rules can be interpreted as follows: if A and B
shared key K and A sees message, then A believes that
this message are from B.
2. Nonce rule
if (A| ≡ #(X), A| ≡ (B X )) then A| ≡ (B| ≡ X).
The rules can be interpreted as follows : if A believes
that X is ”current” and that B said X , then A believes
that B believes X.
3. Jurisdiction rule:
if (A| ≡ (B| ⇒ X), A| ≡ (B| ≡ X) then A| ≡ X
The rule can be interpreted as follows: if A believes
that B has jurisdiction over X and A believes that B
confirms X then A believes X.
4. Vision rule - Type I :
if (A| ≡ (A ↔
K
B), A {X}
C
K
,C 6= A) then A X.
The rule can be interpreted as follows: if A and B
shared the key K and A sees the message X, encrypted
by the shared symmetric key, and the encryption was
done by another A user then A sees X.
5. Freshness rule :
if #(X) then #(X,Y ).
The rule can be interpreted as follows: if X is fresh
then X ∧Y is also fresh.
Due to the determined character of attribute number
la and their binary form, the number of security state
(level) is strictly defined and equal to 2
la
. The cre-
ated node, in the investigation process (accompanied
to communication run realization), saves its structure
but changes its values of attributes (and consequently
the security state). Security level can only decrease.
In the proposed parallel system for selected security
elements (the so called main security factors) differ-
ent, independently converted, security nodes are cre-
ated. Generally, this situation is presented as in fig.
3.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
238

Figure 3: Security modules (security node structures for dif-
ferent main factors) are built on the basis of chosen attribute
sets. Each module (bold frame) consists of a different set of
attributes.
3 PROBABILITY - TIME
AUTOMATA AS
COMMUNICATION SECURITY
INVESTIGATION MODEL
It is proposed to use probability - time automata
(PTA) and converted to them colored Petri nets as
main tools for the investigation communication secu-
rity according to selected main factors, such as: proto-
cols, users, keys, messages, etc. The nodes presented
in fig.1 will be the fundamental part of PTA (and Petri
nets). Let us introduce the definition of the security
state which will correspond to the automaton node.
Definition 1. A tuple (At, T h, T k,na),
where:
At - security attribute set,
T h - the vector of the low level of feasible attribute
values (thresholds),
T k - security tokens,
na - the number of attributes, is the communication
security state described as follows:
1. At = {at
1
,at
2
,..., at
n
} ∈ [0,1]
n
- the vector of at-
tribute activation probabilities,
2. T h = {th
1
,th
2
,...,th
n
} ∈ [0, 1]
n
- the vector of a
threshold attribute activation (acceptation),
3. T k = tk
1
,tk
2
,...,tk
n
∈ {0,1}
n
- the binary vector of
an attribute activation:
if at
i
≥ th
i
then tk
i
= 1 otherwise tk
i
= 0.
Global structure of this automata is presented in fig.4.
To regard the time parameter which is an intrinsic
characteristic according to the security aspect, the fol-
lowing definition is proposed:
Definition 2. A probabilistic timed automaton
PTA is a tuple of the form
(L,l
0
,X ,
∑
,inv, p), where:
Figure 4: The scheme of probabilistic - time automaton for
communication security investigation, where p(i, j) - the
probability of state changing: from state i to j; j ≥ i.
- L is a finite set of locations,
- l
0
∈ L is the initial location,
- X is a finite set of clocks (for each attribute),
-
∑
is a finite set of possible steps, where
∑
c
∈
∑
are
declared as being current possible,
- the function inv : L → CC(X) is the invariant
condition,
- the finite set p ⊆ L ×CC(X) ×
∑
×Dist(2
X
× L) is
the probabilistic edge relation.
A time state of a probabilistic timed automaton is
a pair (l,v) where l ∈ L and v ∈ T
X
are such that
v ∈ inv(l). Informally, the behavior of a probabilistic
timed automaton can be understood as follows. The
model starts in the initial location l
0
with all clocks set
to 0, that is, in the state (l
0
,0). In this, and any other
state (l,v), there is a nondeterministic choice of either
(1) making a discrete transition or (2) letting time
pass. In case (1), a discrete transition can be made
according to any probabilistic edge (l, g,σ, p
∗
) ∈ p
with source location l which is enabled; that is, the
zone g is satisfied by the current clock valuation v.
Then the probability of moving to the location l”
and resetting all of the clocks in X to 0 is given by
p
∗
(X,l”). In case (2), the option of letting time pass
is available only if the invariant condition inv(l) is
satisfied while time elapses and there does not exist
an enabled probabilistic edge with a current step.
Note that a timed automaton (Alur and Dill, 1994),
(Beauquier, 2003) is a probabilistic timed automaton
for which every probabilistic edge (l, g,
∑
, p
∗
) is such
that p
∗
= µ(X,l”) (the point distribution assigning
probability 1 to (X,l”)) for some (X,l”)∈ 2
X
× L.
Additionally, the recognition of the number of
users and their character (honesty, intruder) (Bur-
ParallelSimulationofDynamicCommunicationProcessesontheBaseofProbabilityTimeAutomata
239
rows et al., 1990) is wanted. These considerations
are based on time influences on chosen security at-
tributes; strictly on their level (value). Time influ-
ences may refer only to specific attributes, such as:
keys, nonces, secrets. The investigation consists in
finding the typical actions, being directly connected
with attributes, in protocol operations and defining the
way of their influences on the attribute value. So, for
each message the time state will be defined as a set of
pair(l
i
,v
j
), where i- the number of a node (operation
in a run), j- the code of attribute. The location l
i
will
be referred to an automaton node which is equivalent
a number of the realized protocol operation (strict op-
eration in communication run). On this stage the com-
munication run is defined.
Definition 3. The time sequence of protocols op-
erations whose elements e
i
are represented by actions
set A
i
= {a
1
,a
2
,..., a
lac(i)
}
i
correcting node attributes
At
i
= {at
1
,at
2
,..., at
la
}
i
(where i - the number of op-
eration in communication run, j- the number of se-
curity attribute, lac(i)- the number of actions, la - the
number of security attributes), which is equivalent au-
tomaton steps (nodes) and can belong to different pro-
tocols and messages is named the communication run:
oi(k, s) → At
i
(k, m), (1)
where:
o(k, s) - s-th operation in k-th protocol,
k - protocol number,
s - operation number in protocol,
m - message code.
It can be noticed that e
i
= {o(k,s)|k = 1,2,..., l p, s =
1,2, ...,ls(k)}, where l p - the number of protocols,
ls(k) - the number of operations in k protocol, and
∀
k
∀e
j>i
(s
j,k
> s
i,k
), i.e. for given k protocol oper-
ations should save a given order. For different pro-
tocols k 6= h∀e
j>i
((s
j,k
> s
i,h
) ∨ (s
j,k
< s
i,h
) ∨ (s
j,k
=
s
i,h
)). Each operation consist of actions a
α(r,s)
r
, where
α(r,s) ∈ {0, 1}, r - the code of action. It can be said
that α(r,s) refers to the present (activation) concrete
action in s-th operation: if α(r, s) = 0 action a
r
is not
present in s-th operation, otherwise r-th action is acti-
vated in this operation.
o(k, s) = {a
α(r(1),s)
r(1)
a
α(r(2),s)
r(2)
,..., a
α(r(1),s)
r(la(s))
}, (2)
where:
r(1), r(2),..., r(la(s)) - the sequence of action codes
in s-th operation,
la(s) - the number of actions in s-th operation.
Generally, a number of actions cannot be ordered in
different operations because only after the operation
is finished the values of state security attributes will
be modified. Therefore, it is proposed to create a sta-
ble list of actions which will be activated for a partic-
ular operation. Transition to new automaton node is
realized by correction node attributes with the help of
the action set of the current ended operation.
4 PARALLEL PROCESS OF
CORRECTION
COMMUNICATION SECURITY
ATTRIBUTES
The corrections of attributes can be realized simulta-
neously. The new recognized action is used with the
help of communication logic rules to activate the set
of attributes. At this moment adequate processor units
start to correct the clock and value of attributes. After
the correction, the medicated attribute is sent to dif-
ferent processors analyzing communication security
level in accordance with particular main factors. The
estimation of acceleration inferring from paralleliza-
tion can be defined as acc = la ∗ (1 + lm f )/2, where
lm f - the number of main factors. The number of
main factors is the sum of number of selected proto-
cols, messages, keys, users, nonce’s (see fig.3). The
main security factor(s) is (are) declared for the current
action. Action usually influences one or several at-
tributes. Analyzing security situation in network sev-
eral (their number is e.g. equal lac) processors can
serve set of communication actions. Therefore, the
acceleration parameter will be estimated as interval
in following way:
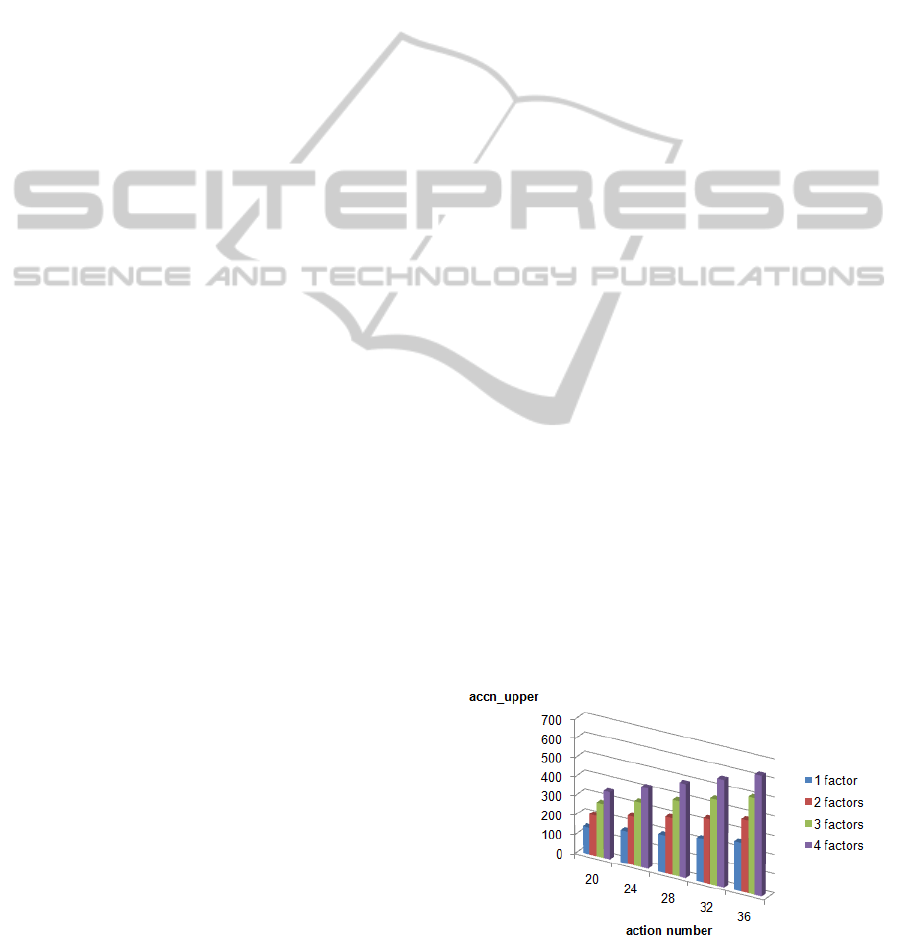
accn = [la ∗(1 + lm f )/2;lac ∗la ∗(1+ lm f )/2]. (3)
The upper bound of acceleration (fig.11) is achieved
when the sets of attributes, evoked by actions, are mu-
tually independent: set
a
t(i) ∪ set
a
t( j) = , i, j - the
number of actions (Tudruj and Masko, 2005).
Figure 5: The upper bound of acceleration accn in parallel
security checking variant.
The stages of this algorithm are as follows:
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
240
1. action input,
2. the recognition of the attribute corrected by the
action,
3. the recognition of the type of correction,
4. correction realization*,
5. go to the 3-rd point until the last attribute,
6. the recognition of the main factor activated by the
action,
7. token structure creation for the main factor**,
8. security state estimation for the main factor**,
9. go to the 6-th point until the last factor,
10. auxiliary analysis (threaten state prognosis cre-
ation, the distribution of probabilities of transi-
tions to the next stages)**,
11. go to the 1-st point until the last action***.
There are three stages of parallelization: *- simul-
taneous corrections of attributes, **- simultaneous
main security factor analysis, ***- the simultaneous
serving of actions.
The type of action influences is practically regarded
by two forms of algorithm attribute corrections:
mc = {0,1} - correction by multiplication by a given
updating coefficient MCC in case logic and heuristic
rules influence, mc = 1 - the activation this form of
attribute correction, mc = 0 - the rejection this form
of correction.
ec = {0,1} - correction by exchanging to current level
(represented by current coefficient value of ECC) in
case of lifetime or users(intruders) influences.
Therefore, it is possible to use simultaneously two
form of correction for single attribute. So, if ec = 1
then attribute value does not have to be increased:
at
t=k+1
(i)
mc=0, ec=0
→ at
t=k
(i),
at
t=k+1
(i)
mc=1, ec=0
→ at
t=k
(i) ∗ MCC,
at
t=k+1
(i)
mc=0, ec=1
→ ECC,
at
t=k+1
(i)
mc=1, ec=1
→ min{at
t=k
(i) ∗ MCC,ECC}.
The experiments have approved that heuristic rules
that influence in specific cases (for example in multi
usage of the same nonce) are more effective when cor-
rection is realized in the following way:
at
t=k+1
(i)
mc=1, ec=0
→ at
t=k
(i) ∗ (1 − MCC),
or
at
t=k+1
(i)
mc=1, ec=0
→ at
t=k
(i) ∗ (1 − at
t=k
(i)).
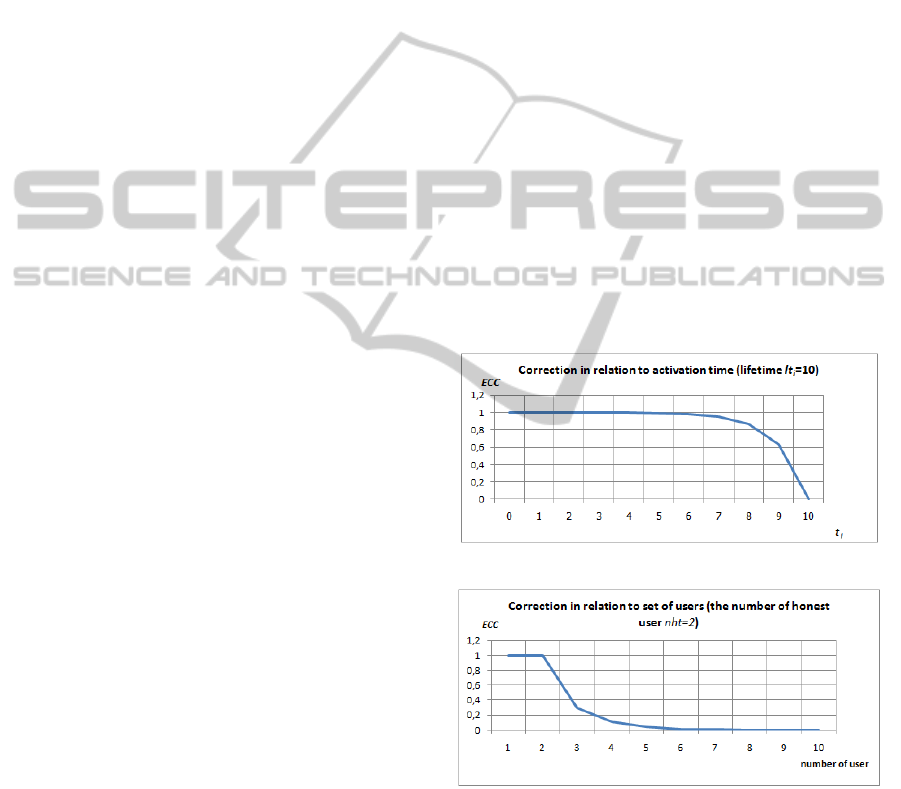
The actual value of ECC, in case of lifetime type of
influence, will be counted by formula:
ECC = 1 − et
t
j
−lt
i
, (4)
where:
t
i
- the time of attribute activation,
lt
i
- the attribute lifetime.
In reality, the time activity is transformed into prob-
ability attribute value, in accordance with the given
attribute lifetime (fig.6).
The actual value of ECC in case of additional users
(intruders) type of influence will be counted by for-
mula:
ECC = i f (nus < nht) then ECC = 1, (5)
else
ECC = e
nht−nus
,
where:
nus- the number of users (in the environment of main
security factor),
nht - the number of honest users.
In reality, the time activity is transformed into proba-
bility attribute value, according with the given number
of honest users (fig.7).
Figure 6: The action time influence on attribute.
Figure 7: The action users influence on attribute.
5 CONCLUSIONS
The security investigation is acquiring an increasing
importance with the growing network communica-
tion. Therefore, the problem of dynamic security esti-
mation is increasingly grasping the interest of the data
ParallelSimulationofDynamicCommunicationProcessesontheBaseofProbabilityTimeAutomata
241

mining community (Szpyrka and Szmuc, 2006). The
parallel approach guarantees not only the possibility
to accelerate the reaction on impending threatens but
also permits to treat chosen main security factors in-
dependently and simultaneously provide security at-
tribute corrections as the result of the effect of influ-
ence on the same protocol actions (Tudruj and Masko,
2005).
REFERENCES
Alur, R. and Dill, D. L. (1994). A theory of timed automata.
Theoretical Computer Science, 126:183–235.
Beauquier, D. (2003). On probabilistic timed automata.
Theor. Comput. Sci., 292(1):65–84.
Burrows, M., Abadi, M., and Needham, R. (1990). A
logic of authentication. ACM Trans. Comput. Syst.,
8(1):18–36.
Kwiatkowska, M., Norman, G., Segala, R., and Sproston,
J. (2002). Automatic verification of real-time sys-
tems with discrete probability distributions. Theoreti-
cal Computer Science, 282:101–150.
Szpyrka, M. and Szmuc, T. (2006). Verification of
automatic train protection systems with rtcp-nets.
In Proceedings of the 25th International Confer-
ence on Computer Safety, Reliability, and Security,
SAFECOMP’06, pages 344–357, Berlin, Heidelberg.
Springer-Verlag.
Tadeusiewicz, R. (2011). Introduction to inteligent systems,
chapter no 1. In The Industrial Electronic Handbook,
Wilamowski B.M., Irvin J.D.(Eds.), pages 1–12. CRC
Press Boca Raton.
Tudruj, M. and Masko, L. (2005). Towards massively par-
allel numerical computations based on dynamic smp
clusters with communication on the fly. In Parallel
and Distributed Computing, 2005. ISPDC 2005. The
4th International Symposium on, pages 155–162.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
242
