
A Simulation Fidelity Assessment Framework
Sangeeth saagar Ponnusamy
1,2
, Vincent Albert
2
and Patrice Thebault
1
1
Airbus Operations SAS, 316 Route de Bayonne, 31060, Toulouse, France
2
LAAS-CNRS, 7 Avenue du Colonel Roche, 31077, Toulouse, France
Keywords: Abstraction, Compatibility, Experimental Frame, Formal Matching, Bisimulation, Galois Connection,
Ontology, Simulation.
Abstract: A proposition for the correct by design of abstraction with respect to the simulation objectives based on the
concepts of approximate bisimulation, Galois connections and ontology is presented. It addresses the
fundamental problem of fidelity in simulation, namely, given a class of models and a class of properties that
must be preserved, how to extract modeling abstractions that preserves the properties of interest which
allows to conclude about the system being simulated. Fidelity and validity are explained in the framework
of the experimental frame and discussed in the context of modeling abstractions. A formal method for the
fidelity quantification is explained by abstraction inclusion relations for syntactic and semantic
compatibility. Abstraction inclusion in dynamic systems for semantic compatibility by approximate
bisimulation and the problem of finding surjection maps compatible with simulation objectives are
discussed. Syntactic compatibility is explained by ontologies followed by a brief discussion on the Galois
connections and building Galois surjections compatible with the simulation objectives at the end.
1 INTRODUCTION
Modeling and Simulation (M&S) are the analysis
and decision means to assess performances,
functionalities and operations of a system of interest
(Brade, 2004). Simulation is increasingly being used
as a means to design and analyze real world complex
systems, and hence, a Model Based Systems
Engineering approach is important in development
and usage of simulation products. In the context of
systems engineering, Verification and Validation
(V&V) determine the compliance of simulation
products with their specifications and fitness for
their intended use respectively. However, a ‘distance
to reality’ requirement is seldom expressed even if
the context of use is well known.
The effectiveness of simulation in reproducing
the reality i.e. realism of simulation, motivates the
following questions:
• How to quantify the distance between a
system and its simulation with respect to its
V&V objectives?
• Regarding the V&V objectives, what are
the fidelity requirements on the means of
simulation?
• How to develop simulation models with
respect to fidelity requirements?
• How to develop a consistent approach to
the evaluation of fidelity of simulation
models along the product development
cycle?
In the model based design approach,
effectiveness largely depends on the degree to which
design concerns captured in the different abstraction
layers by different stakeholders are orthogonal, i.e.
how much the design decisions in the different
layers are independent (Clark, 2013). Thus it is
necessary to capture and implement modeling
abstractions consistent with the design objectives.
This paper describes a formal proposition for finding
and implementing modeling abstractions compatible
with simulation objectives in the established M&S
framework by Zeigler (Zeigler, 2000) using concepts
from control and computer theory such as
approximate bisimulation (AB) (Girard, 2007),
abstract interpretation (AI) (Cousot, 1992) and
ontology (Wagner, 2012). The concepts of fidelity
and abstractions are briefly explained followed by
proposition on formal approach in the modeling and
simulation context.
463
Ponnusamy S., Albert V. and Thebault P..
A Simulation Fidelity Assessment Framework.
DOI: 10.5220/0005105704630471
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),
pages 463-471
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 ABSTRACTIONS & FIDELITY
Abstraction is an operation mapping a system
described by differential equations, logical
statements etc. onto another abstract system,
whereby all what is true about the abstract system is
true of the original system, but, the converse is not
necessarily true. A model is always an abstraction of
the reality and this modeling abstraction is the
causative of fidelity with an inverse relation. In
using simulation for system design and V&V
activities, the model and its level of abstraction
should be coherent to derive any meaningful
conclusion from the simulation results about the
system. In modeling and simulation of complex
systems, often the difficulty is finding and
implementing consistent and valid abstractions to
model the simulated system with respect to
simulation requirements. This is more so true in
developing a complex simulation product where the
component models can be developed by different
stakeholders and a common frame of reference must
exist in terms of implementing consistent
abstractions in the experimental frame.
2.1 Experimental Frame
In the context of studying a system through
simulation, the concept of experimental frame (EF)
introduced in (Zeigler, 1984) is used to describe
experimental scenarios under which the System
Under Test (SUT) will be used. An EF defines
controllability and observability means to stimulate
and observe the model temporal evolution in
addition to conditions of experimentation.
An Experimental Frame, in general, is composed
of primary components called generator (G),
transducer (T) and acceptor (A) and, secondary
components called environmental model which
simulate the real environment in which the SUT
operates. The components could be interconnected
and hierarchically composed to build an EF. Let us
denote the EF as
EF=EF
⋃EF
(1)
where EF
= { M
P
∣ P={G,T,A}
EF
S
= M
S
∣
∣
S=
1,2…S
N
refers to the primary and secondary EF components
respectively.
The components models in Eq.1 are given as
M
P,S
=<T,X
P,S
,Y
P,S
>
(2)
where P={G,T,A ,S=
1,2…S
N
, X and Y are input
and output variables defined over a time base T.
The concepts of homomorphism, applicability
and derivability were proposed by (Zeigler, 1984) in
the framework of M&S. Morphism relation
establishes behavioural equivalence between a
concrete model and its abstraction. Applicability and
derivability defines a compatibility criterion between
a model and EF, and also between two experimental
frames. A fidelity framework needs to address
consistent abstractions for morphism relation. In
addition, as a prerequisite for validity assessment,
the framework needs to address whether the EF can
meet simulation objectives and whether the model
can work with the EF.
The abstractions made when the model is built
must match a set of acceptance conditions given by
the experimental frame (Ponnusamy, 2014). An
experimental frame typology could be thus found by
having equivalence classes according to the system
considered (system, equipment, type of system,
software, etc.) and the system properties
(performance, robustness etc.) targeted by the V&V
activity (Albert, 2009). Thus, the objective will be to
define a way of formally quantifying the fidelity of a
simulation and to define a methodology for finding
and implementing the abstractions consistent with
the simulation objectives.
2.2 Validity in Experimental Frame
A model is said to be valid if it is representative
enough of the system it represents and satisfies the
experimental frame. In this context of definition of
validation requirements, it is important to distinguish
between simulation validity and system validity.
Simulation validity answers whether the simulation
is adequate to answer questions on system
validation. System validation is validation of system
with respect to its requirements. Simulation validity
is a prerequisite of system validity and thus
decisions taken at any stage along the V cycle where
simulation is used as a means of V&V is
intrinsically tied to the key question of simulation
fidelity. A system is said to be valid by simulation
only when the simulation itself is valid and thus it is
a necessary and sufficient condition for system
validity assessment through simulation. Let φ
and φ
be system and simulation requirements
respectively on the system (S
) and its
representation (S
). The system validity
assessment by simulation thus becomes
φ
i=1..n
φ
⋃φ
(3)
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
464
In this context, in (Albert, 2009), experimental
frames were proposed in terms of model usage
domain and model objective domain called
Simulation Domain of Use (SDU) and Simulation
Objective of Use (SOU) respectively. In other
words, SOU is the frame of experimentation and
SDU is the frame of the developed simulation i.e.
model capabilities.
Simulation validity in other words can be defined
as the compatibility between an SDU and an SOU.
Compatibility is discussed in terms of validity
through abstraction. In simulating a complex system
which is hierarchically composed of different
subsystems, modeling abstraction choices in
building an SDU consistent with simulation
objectives described by an SOU will yield this
compatibility.
The compatibility is discussed in terms of
reachability of the SUT where reachability is defined
as the set of all possible states reachable by a system
and is used to verify temporal logic properties
defined as safety etc. A study on the abstraction of
the primary EF components,EF
, with respect to
the SOU and a validity assessment methodology in
terms of trace inclusion was proposed by
Ponnusamy et al (Ponnusamy, 2014). However this
study deals with abstraction itself rather than its
effect on validity assessment. The paper is focused
on the development of systematic abstraction and
formal abstraction compatibility criterion of the EF
components in the framework of simulation fidelity.
Essentially, the philosophy of current study is
correct ‘by design’ in that the simulation product
(SDU) designed is “correct (i.e. faithful) by design”
which exhibit behaviour consistent with respect to
the simulation requirements (SOU) through the
implementation of abstractions.
In abstraction of a system and its validation
against the specifications, different classes of
abstractions (SDU) on four axes of architecture,
data, computation & time were proposed by Albert
(Albert, 2009). Similar such definition can be
extended to class of specifications (SOU) and a
unified formal fidelity framework will have to
encompass all such classes and defines a quantitative
compatibility criterion between the class of
abstractions and specification. Thus fidelity
assessment through abstraction compatibility means,
given a class of models (e.g.: hybrid), and a class of
properties that must be preserved (e.g.: safety),
extract modeling abstractions (e.g.: state
aggregation) that preserve the properties of interest.
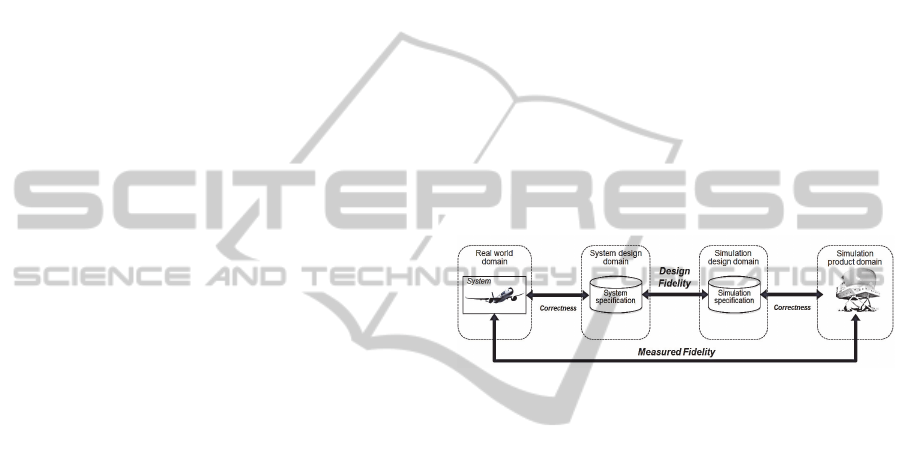
2.3 Design & Measured Fidelity
Fidelity is often used in different contexts both in
scientific and non-scientific fields alike, and myriad
interpretations of fidelity, especially in the M&S
community, leads to inconsistency in the V&V
activities which necessitates a precise notion of this
generic term. In this paper, Fidelity is defined as a
notion of distance to reality and this is akin to the
definitions by Implementation Study Group (ISG) of
Simulation Interoperability Standards Organization
(SISO) (Gross, 1999). Based on this notion, fidelity
could be classified into design fidelity and measured
fidelity. Design Fidelity is defined as the distance
between the system specification and the simulation
specification, whereas, Measured Fidelity is the
distance between the real system and the simulation
product. These concepts are illustrated below in a
simulation product development cycle.
Figure 1: Design & Measured Fidelity.
Current method of system validation through
simulation is a process based on measured fidelity.
This conventional bottom up approach necessitates
the knowledge of executability of the V&V plan on
the means of simulation and confidence of the
results. Fidelity requirements (expected capabilities,
tolerances etc.) are not explicitly represented in the
system V&V plan and fidelity assessment is relied
upon by traditional but arduous method based on
high end expertise review and past experience.
Challenges in complexity, methodology and
continuous evolution of change in product
requirements often makes model development an
iterative process and in this paper we attempt to lean
this modeling process by quantifying the relation
between model abstraction levels and its associated
validity requirements. This is essentially a paradigm
shift from a process based on measured fidelity to a
process based on design fidelity.
2.4 Fidelity Quantification
Model Fidelity,M
, is the distance of the SDU from
the real system. Simulation fidelity, S
, and
simulation model fidelity, M
, are different with the
former being affected by factors such as the model
ASimulationFidelityAssessmentFramework
465

of computation (C), execution platform (P) etc.
which are not discussed in the scope of our study.
Thus the simulation fidelity is the aggregation of all
component fidelities, S
F
=
∑
(ΣM
F
+P
F
+ΣC
F
+...)
Fidelity, resulting from abstraction, is based on
both the SUT type and type of operation (SOU). It is
to be noted that the fidelity per se is an absolute
realism measure of the SDU (what the model can
do) independent of the SOU (how the model is
intended to be used). However, an absolute
definition of fidelity is neither feasible nor useful
since a model is always abstracted with an objective
behind (Gross, 1999), (Brade, 2004), (Roza, 1999).
A more pertinent question is what is the right level
of abstraction for the Intention Of Use (IOU)? Or
succinctly, how do we formally relate fidelity and
validity?
Let ε be this distance notion, hitherto referred to
as abstraction precision. Then absolute model
fidelity can be defined as,
M
ε
ε
(4)
where
denotes the EF modeling abstraction
precision with an unknown additional precision, ε
,
implied by multitude of factors such as modeling
formalism, layer of abstraction etc. Instead of an
absolute measure, a relative measure called the
relative fidelity or simulation model fidelity which is
defined as a measure of closeness of abstraction
between the SOU and SDU is introduced as follows,
M
ε
/ε
(5)
If
=1, then it is at the right level of abstraction
and
1, then the abstraction is too precise
(over fidelity) and vice versa. Alternatively the
validity (pseudo) metric,
says how
close the abstractions are with the key question can
fidelity be measured as precision of abstraction as
described.
It may be reminded that the SDU abstraction is
valid if it is compatible with the SOU abstraction.
But the level of compatibility yields a measure of
required abstraction. Consider a system of order
5 abstracted to
2 with
3. This
is a case of over abstraction with respect to objective
as
1. However if the objective is different,
say
1,then it is a case of under abstraction
with
1. Thus the correct abstraction is
subjected to the SOU definition i.e. a model may
have low fidelity but still be valid.
Consider an another simple example, let us
assume an ideal system output of Y
1° at
interface of the SUT, which is abstracted by the
SDU and SOU as range of values, an interval
abstraction defined by [minmax]. The abstraction is
valid if the acceptable range is bigger than the
available range and relative fidelity is high as the
two ranges are closer.
Required fidelity is expressed via allowable
abstractions and indirectly in terms of required
relative fidelity. Two key perspectives for formal
fidelity assessment method emerge here, namely,
verification & synthesis. In a verification
perspective, a formal fidelity quantification method
yields the validity pseudo metric or relative fidelity
for a given SDU abstraction. The key idea is: are my
abstractions compatible with a metric assigned on
its compatibility? Instead, in synthesis perspective,
for a required fidelity defined by the SOU, a formal
fidelity method gives a necessary and sufficient
SDU abstraction. The key idea here is: what are my
compatible abstractions with respect to a metric?
Consider first example, it is akin to asking what is
(a modeling rule) for a given fidelity
requirement. This correct ‘by design’ synthesis
approach is the objective of the study.
3 FIDELITY FRAMEWORK
In general, implementation of the fidelity framework
is twofold, capturing and assessing fidelity.
Capturing fidelity needs refers to the collection of
fidelity requirements from the SOU in terms of
allowable abstraction or required abstraction
precision. Assessing fidelity refers to quantitative
assessment by a formal abstraction compatibility
criterion between allowable and implemented
abstractions i.e. SOU and SDU respectively.
The assessment is based on the framework of
finding consistent abstractions compatible with
simulation objectives and there exists two
perspectives called semantic and syntactic
compatibility based on the behavior and structure of
models respectively. Class of abstractions and
specifications could be mapped with those two
hierarchical layers and propositions for compatibility
are explained based on the concepts of AB and
ontology for each perspective.
It may be recalled that a morphism relation
establishes correspondence between a concrete
model and its abstraction through abstraction
operation. Abstractions are manyfold depending on
the simulation objectives and hypotheses. From the
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
466
classes of abstractions defined in (Albert, 2009), we
define abstraction operation as α over an abstraction
class. The validity of the SDU abstraction against
the SOU is defined by abstraction inclusion. An
abstraction inclusion relation could be formalized by
defining a partial order on abstractions. A partially
ordered set or a poset is a set P = (≼, S) with
reflexive, transitive relation on a set S. The
hierarchy of abstractions could be defined as a
partial order relation over a finite lattice. This would
serve as a baseline for model developers to choose
the modeling rule and, for users to choose the model
on a V&V platform, with sufficient fidelity. In
addition, it would be beneficial if common modeling
rules for models with respect to the IOU were
identified which helps in reusability of existing
models and better utilization of resources. Such a
framework would help in traceability between the
system specifications and the IOU. The proposed
framework is briefly illustrated in the following
figure.
Figure 2: Fidelity Framework.
3.1 Semantic Compatibility -
Approximate Bisimulation
Framework
Semantic compatibility refers to the abstraction
resulting in abstract semantics compatible with the
simulation objectives. More precisely, the focus is
on abstractions of data class, state aggregation type
in model order reduction of dynamic systems using
AB relations developed by Pappas, Girard et al
(Girard, 2007) within the framework of metric
transition systems. A metric transition system is a
transition system whose outputs are equipped with a
metric such as the Euclidean distance. Consider two
transition systems T
,
which essentially refer to a
concrete EF model and its abstraction defined in
Eq.2 as,
T
=< S
, X
, Ʈ
, S
, Y
,
> , n=1,2
(6)
where
S
are the set of states
X
are the set of inputs
Ʈ
are the transition maps, Ʈ
: S
X
→2
S
are the set of initial states S
⊆ S
are the output maps
∶S
→Y
equipped with a
metric d.
AB relations are intended to capture the most
significant characteristics of a system dynamics and
neglect the less important ones (Girard, 2007). The
degree of approximation is given by the precision of
the AB function (ε) and this precision provides a
bound of the distance between the output trajectories
of a system and its abstraction. The set of output
trajectories, Y,X∣ YS, denoted by T is
called the language of the transition system, T. The
behavioral equivalence by homomorphism relation
described in section 2.1 is given here in terms of the
observational equivalence i.e. language inclusion
and equivalence.
From (Girard, 2007), two metric transition
systems T
and T
are said to be bisimilar with a
precision ε, if there exists bisimulation relation,
ε
and for all (s
,s
)∈
ε
dO
1
s
1
, O
2
s
2
ε
{ ∀ x ∈ X, ∀ s
1
'
∈ S
1
(s
1
,x) ,
∃ s
2
'
∈S
2
(s
2
,x) ∣ (s
1
'
,s
2
'
∈
ε
{ ∀ x ∈ X, ∀ s
'
∈ S
(s
,x) ,
∃ s
1
'
∈S
(s
,x) ∣ (s
1
'
,s
2
'
∈
ε
(7)
Such bisimulation relations could be expressed
as bisimulation function, ƒ
. The function ƒ
:S
S
→
is a bisimulation function between T
and
T
, if for all (s
,s
)∈S
S
ƒ
s
,s
max
dO
1
s
1
, O
2
s
2
,
sup
x∈X
s
1
'
∈S
1
(s
1
,x)
inf
s
2
'
∈S
2
(s
2
,x)
ƒ
B
(s
1
'
,s
2
'
,
sup
x∈X
s
2
'
∈S
2
(s
2
,x)
inf
s
1
'
∈S
1
(s
1
,x)
ƒ
B
(s
1
'
,s
2
'
(8)
where the bisimulation function ƒ
bounds the
distance between the observations for a couple
(
s
,s
) by precision ε 0 such that ƒ
s
,s
ε
and non-increasing under operational dynamic
conditions.
Capture
Objectives of
Simulation
Specify
necessary &
sufficient
simulation
product design
SDU
SOU
Deliver metrics &
criteria onto validity
of intended use &
simulation product
design
ASimulationFidelityAssessmentFramework
467

Applications of AB include bisimulation metrics
for linear systems, abstractions of hybrid systems
and hierarchical control design. A correct ‘by
design’ of embedded control software using
bisimulation relations was implemented by tools
such as PESSOA (Mazo, 2010) and CoSyMa (Sebti,
2013) by expressing requirements in temporal logic.
The current approach is inspired from such work and
attempts to derive abstractions based on required
precision of abstraction rather than the other way
around.
AB is more amenable for applications such as
safety verification since transient dynamics are
included in abstraction and error bounds are based
on L
norm unlike classical model reduction
frameworks (Girard, 2007). This error bound or
precision of abstraction can be related to fidelity
requirement and thus gives a framework in
synthesizing abstraction yielding required precision.
By relating the desired precision mandated by the
simulation users (SOU) with implemented precision
by the model developers (SDU) through a formal
framework, fidelity could be quantified.
Proposition 1: Let
and
be
abstractions of SDU and SOU with precision
and
respectively, a simulation product is said
to be faithful if the developer abstractions are more
precise than user abstractions i.e.
⪯
.
From the definition of the EF specification in
Eq.1, let us denote the concrete system (M
), its
reference abstraction M
and implemented
abstraction M
. The V&V cycle can be
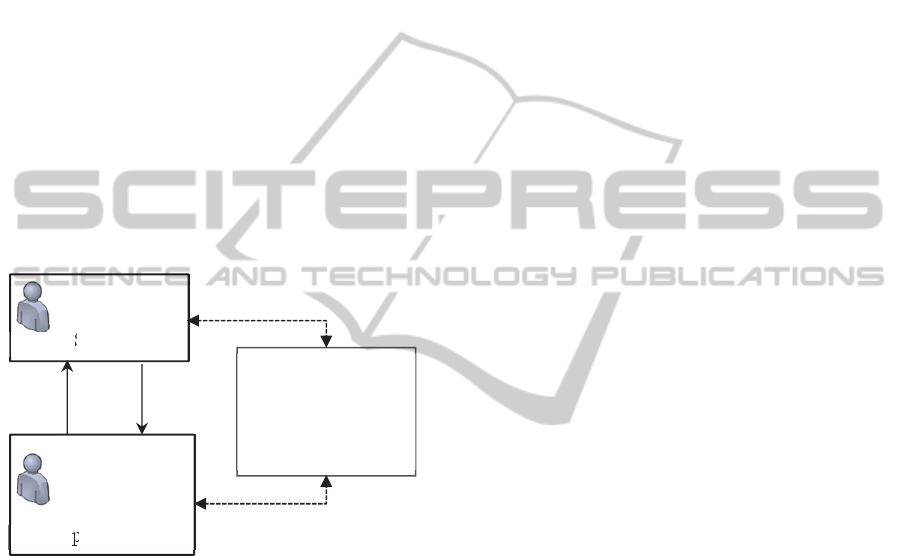
illustrated in terms of such hierarchical abstraction
and requirements in Figure 3. The diagram can be
interpreted as follows, a concrete system (M
) is
said to be valid if it satisfies the system
requirementsφ
and denoted by M
.
Similarly M
and M
are defined for the
SDU and SOU respectively with respect to the
simulation specification, φ
.
Figure 3: Abstraction in Modeling & Simulation.
A fidel simulation allows to conclude about
M
by studying M
derived from
M
.Thus the objective is to develop M
consistent with M
to answer questions on M
.In
validity assessment of system by simulation, the
simulation user i.e. SOU defines a set of acceptable
abstractions (α
resulting in model behavior
representing the system. The model developer i.e.
SDU, based on system specification and simulation
specification, develops models implementing
abstractions (α
resulting in a certain model
behavior consistent with simulation objectives. The
question of requirement validation is not addressed
here and it was assumed that the given simulation
requirements are valid with respect to its system
requirements.
It is known that an abstraction operation is
essentially a modeling rule to reduce the complexity
of a model and to have a simulation model with
sufficient fidelity, the abstraction mandated by the
SOU must be compatible with the one actually
implemented by the SDU. In the framework of
fidelity, the abstraction inclusion can be interpreted
in verification as well as a synthesis perspective. The
simulation specification lays out the required rule in
terms of precision of abstraction, ε
SOU
allowed or
the reference abstraction, M
SOU
itself. In the former
case it becomes a verification problem such that the
precision of allowable abstraction, ε
SOU
, is checked
against the abstraction implemented, M
SDU
,
ƒ
M
c
,M
SOU
=ε
SOU
ƒ
M
c
,M
SDU
=ε
SDU
(9)
Then, by definition of inclusion, a simulation
model is valid when ε
SDU
⪯ε
SOU
. In other words,
the unknown reference model M
is verified
against implemented model M
through the
precision of abstraction. Properties such as safety
could be verified through reachability analysis using
an adaptation of discrete verification techniques to
the continuous context, namely, computing by
geometric means an over-approximation of the set of
states reached by all trajectories. Various approaches
to reachability computation and their applications
can be found in (Stursberg, 2003), (Tomlin, 2003),
(Maler, 2002).
In the latter case, namely synthesis, for a given
precision, ε
SOU
, a corresponding user abstraction is
found, M
SOU
.
ƒ
M
c
,ε
SOU
= M
SOU
(10)
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
468

Then it is essentially a problem of correction i.e.
implementation of reference model
as
in
the environmental model. However, the SOU is
seldom expressed as a reference model and is
usually expressed in terms of acceptable error
tolerances. Intuitively, acceptable abstractions are
indirectly expressed as acceptable error tolerances.
Interpreting such error tolerances as precision of
abstraction in the context of AB, the question would
be given acceptable error tolerances what are the
necessary and sufficient abstractions consistent with
the SOU such that M
~M
.
This implies that abstraction is finding a
surjection map and valid abstraction is finding the
surjection map consistent with the SOU.
Let,α:R
n
1
→R
n
2
, be an abstraction mapping a
concrete model,M
c
1
, to its abstract version,M
A
1
,
wheren
1
>n
2
.The hierarchy of abstractions are
related by binary relation forming a partial order as
follows.
M
α
1
→M
… M
(11)
Different such abstractions may be feasible
defined by a set N and the valid set of abstractions
among them are defined by
∀ i∈N,∃α
⊨ {φ
, φ
…φ
}
(12)
where φ
..
are the requirements defined in
formalism such as temporal logic.
In the AB framework, consider abstraction of
linear system M
toM
by α
1
where α
1
is a linear
quotient map. Conditions for the surjection map to
be an observation preserving partition which in turn
is a bisimulation are given in (Pappas, 2003).
Further, in (Girard, 2007), Girard et al remarks that
such an admissible surjective map can be chosen
such that the precision of abstraction formalised as a
semi definite optimisation problem is minimal. The
selection method, however, is based on heuristics
and Girard et al emphasises the need for better
method to find this map such that precision of
abstraction is minimal. In our synthesis approach,
however, the question is to find the surjection map
such that precision of abstraction is arbitrarily closer
to the required precision. The existence of such an
admissible surjection map gives the necessary and
sufficient abstraction consistent with the simulation
objectives.
Proposition 2: For a given fidelity requirement,
defined over some metric,
, the best possible
abstraction precision is given by
~
.
In abstracting concrete semantics, different levels
of abstraction are possible and the best possible
abstraction α
~α
,with respect to required
fidelity is given by distance between the required
precision and available precision of abstraction.
By partial order relation, for abstraction
where 1.. are different levels of model
abstractions, if
M
SDU
i
⪯M
SDU
i+1
M
SDU
i+1
⪯M
SDU
i+2
(13)
Then
M
SDU
i
⪯M
SDU
i+2
The best possible abstraction is the one whose
precision of abstraction is closest to the required
precision.
In addition to abstraction of model semantics,
model interfaces are abstracted based on their syntax
definitions and the semantics they handle. The
syntactic (number of ports, coupling, structure) and
semantic (data type, type signature) of the EF and
SUT interfaces must be compatible and are defined
in terms of a partial order relation. Such a definition
followed by an inclusion criterion will help address
the simulation validity with respect to abstractions.
The ‘correct by design’ abstractions once
constructed will result in model behaviour satisfying
objectives. This can be verified by a model coverage
metric proposed in (Ponnusamy, 2014), (Foures,
2013) to analyse the extent of model coverage
through abstraction.
3.2 Syntactic Compatibility - Ontology
Framework
The syntactic perspective concerns only the structure
of the dynamics and not their effect. Syntactic
compatibility deals with the abstraction resulting in a
structure of the system dynamics consistent with
simulation objectives. This compatibility is equally
important as the current languages of systems
engineering are usually informal (text and pictures)
and semiformal (diagrams and drawings) but seldom
formal (rigorous domain-specific languages). More
formal language usage through such syntactic
compatibility in the system definition will result in
system implementation with less error. Ontology,
ASimulationFidelityAssessmentFramework
469

which is a formal representation of a set of concepts
within a domain and the relationships between those
concepts, can be used in such a definition.
The formal method based on ontologies could
serve as an integrating standard in system modeling
and simulation by organizing and relating analyses
of a design in a consistent manner (Wagner, 2012).
In (Man, 2009) a correct, scalable and automated
method, semantic properties are inferred using
lattice-based ontologies. Similar notion can be
extended to a systems perspective in tools such as
SysML for system and architecture definition. For
the SOU and SDU abstractions of the same class,
abstraction hierarchy forms a partial order relation
for each abstraction class. The compatibility
between two abstractions (SOU and SDU) can be
checked by inferring the precision ordering and by
measuring how far they are apart with help of a
distance metric such as the Hausdorff distance
giving a measure of fidelity (i.e. distance between
abstractions) as defined in section 2.4.
3.3 Galois connection
Galois connections give a mathematical framework
for sound and precise abstractions through
refinement. Galois connections were first used in the
AI framework by Cousot (Cousot, 1992). AI is the
interpretation of program semantics by abstract
values and it expresses connection between the
concrete semantics and abstract semantics using
Galois connection between associated property
lattices. It is to be noted that abstraction can be
defined in terms of homomorphism and its inverse
function giving a Galois connection. In addition,
homomorphism between Kripke structures preserves
the ability to transit between states and in this
context it is referred to as ‘simulation’. Simulation
relations, similar to the one explained in section 3.1
shows the behavioral equivalence and inclusion
between two systems by defining the Galois
connections, and hence, the abstractions. Thus the
AI semantics is similar to bisimulation notion. An
analogy with AI framework used in program
analysis could be drawn as AI is a verification of
specification through concrete domain abstraction.
The abstraction is given by Galois connection
between the concrete semantics defined as least
fixed point over a complete lattice and an abstract
semantics defined over an abstract lattice.
Given a complete lattice of concrete data,C, and
a simpler complete lattice of abstract data, A, the two
domains can be related by abstraction operation,
:C→A and inversely by concretization operation,
γ:A→C.For each functionf:C→C, synthesize
f
#
:A→A, such that α is a homomorphism and thus
concrete semantics is abstracted. In general, (,) is
called a Galois connection if and only if
(c) ⪯ a
c ⪯
(a)
(14)
The Galois connection defines a closure operator
ρ = γ ● α and hence a best abstraction (Cousot,
1992). As a corollary, when is a surjection then it
becomes a Galois surjection. Galois surjection can
thus be used to define the best abstraction for
projection of high dimensional system to its low
dimensional subspace. Soundness and precision
criteria of Galois connection could be useful in
synthesizing such best abstractions with respect to
the SOU. Further studies are being carried out to
ascertain the possibility of synthesizing surjection
map consistent with simulation objectives using
Galois connections.
4 FUTURE WORK
The heuristics based choice of surjection map,
though not an optimal method, yields better
experimental results for verification which in turn is
an iterative procedure to find the valid abstraction
(Girard, 2007). The method proposed in this paper
could alleviate this heuristics problem and yield a
systematic method to choose the surjective map
based on the synthesis or verification objective.
However, further research is needed to integrate
these concepts into a scalable algorithmic
framework applicable to complexity reduction in
dynamic systems. Also worth noting is that other
abstraction parameters such as time, architecture,
scope etc. are not discussed and a comprehensive
abstraction framework will need to include all such
classes to yield a valid model abstraction.
In addition, notion of reachability is more
pertinent than simulation for dynamic systems since
an exhaustive breadth first search of state space
through reachability analysis, difficult though it
might be in terms of computational cost, yields
formal verification of system (Tiwari, 2003).
However, application of such formal methods to
large scale industrial systems which are typically
system of systems with different layers of
abstraction will be incremental and the proposition
described in this paper is one such method for
simulation model development. In reality, simulation
as an enabling method for design and development
of systems will not be replaced by formal
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
470

verification such as reachability, at least not in the
near future and not in some specific domains (e.g.:
HMI, FDI, FEMA etc.). Hence, the onus should be
on model development rather than on the
verification aspects.
5 CONCLUSIONS
A proposition for a mathematical framework in
synthesising abstractions consistent with the
simulation objectives is explained and the next step
would be to develop the theoretical proof and build
tools upon them. Realization of such an objective
will help improve the level of confidence in
simulation results for the system V&V and help
better utilization of simulation resources by selecting
the best available resource according to the test
objectives. Identification of such a consistent and
continuous way to improve simulation products will
help improving product development life cycle
quality while controlling the cost and mitigating
risk.
REFERENCES
Albert, V, 2009, Simulation validity assessment in the
context of embedded system design, PhD Thesis,
LAAS-CNRS, University of Toulouse, Unpublished.
Brade D, VV&A Global Taxonomy (TAXO), 2004,
Common Validation, Verification and Accreditation
Framework for Simulation, REVVA.
Clark M, Koutsoukos X, Kumar R, Lee I, Pappas G J, Lee
P, Porter J, Sokolsky O, 2013, A Study on Run Time
Assurance for Complex Cyber Physical Systems,
Interim Technical Report, AFRL/RQQA, NTIS Issue
No 13.
Cousot, P, 1992, Abstract Interpretation Frameworks,
Journal of Logic and Computation, Volume 2, pages
511-547.
Foures, D, Albert, V, Nkesta, A, 2013, Simulation
validation using the compatibility between simulation
model and experimental frame, Proceedings of the
2013 Summer Computer Simulation Conference,
Society for Modeling & Simulation International,
Vista, CA, Article 55.
Frantz F K, 1995, A taxonomy of model abstraction
techniques, Proceedings of the 27th conference on
winter simulation, pages 1413-1420, Arlington,
Virginia, United States.
Girard A, Pappas G J, 2007, Approximate bisimulation
relations for constrained linear systems, Automatica,
Volume 43 Issue 8, pages 1307-1317.
Girard A, Pappas G J, 2007, Approximation Metrics for
Discrete and Continuous Systems, IEEE Transactions
on Automatic Control, Volume 52, Issue 5, pages 782-
798.
Gross D, 1999, Report from the Fidelity Implementation
Study Group, Simulation Interoperatbility Workshop,
USA.
Kim H, 2004, Reference model based high fidelity
simulation modeling for manufacturing systems, Phd
Thesis, Georgia Institute of Technology, Unpublished.
Lickly B, Shelton C, Latronico E and Lee E, 2011, A
Practical Ontology Framework for Static Model
Analysis, In Proceedings of the ninth ACM
international conference on Embedded software, New
York, NY, USA, 23-32.
Maler O, 2002, Control from Computer Science, IFAC
Annual Review in Control 26(2), pages 175-187.
Man-Kit-Leung, J, Mandl, T, Lee, E A, Latronico, E,
Shelton, C, Tripakis, S, Lickly, B, 2009, Scalable
semantic annotation using lattice based ontologies.
Lecture Notes in Computer Science, Volume 5795,
pages 393-407.
Mazo M, Davitan A, Tabuada P, 2010, PESSOA: a tool
for embedded controller synthesis, Proceedings of the
22nd International Conference on Computer Aided
Verification, pages 566-569.
Pappas G J, 2003, Bisimilar linear systems, Automatica,
Volume 39, Issue 12, pages 2035-2047.
Pola G, Girard A, Tabuada P, 2007, Symbolic models for
nonlinear control systems using approximate
bisimulation, 46th IEEE Conference on Decision and
Control, pages 4656-4661.
Ponnusamy S, Albert V, Thebault P, 2014, Modeling &
Simulation framework for the inclusion of simulation
objectives by abstraction, 4
th
International Conference
on Simulation and Modeling Methodologies,
Technologies & Applications, submitted.
Roza M, 1999, Fidelity Requirements Specification: A
Process Oriented View, Fall Simulation
Interoperability Workshop.
Sebti M, Girard A, Gregor G, 2013, CoSyMA: a tool for
controller synthesis using multi-scale abstractions,
16th international conference on Hybrid Systems:
Computation and Control, HSCC'13, pages 83–88.
Stursberg O, Krogh B H, 2003, Efficient Representation
and Computation of Reachable Sets for Hybrid
Systems, Hybrid systems: Computation and Control,
Lecture Notes in Computer Science Volume 2623,
pages 482-497.
Tiwari A, Shankar N, and Rushby J, 2003, Invisible
Formal Methods for Embedded Control Systems,
Proceedings of the IEEE, Vol 91. No. 1, pages 29–39.
Tomlin C J, Mitchell I, Bayen A, Oishi M, 2003,
Computational Techniques for the Verification of
Hybrid Systems, Proceedings of the IEEE, Vol. 91,
No. 7.
Wagner, D A, Bennett, M B, Karban R, Rouquette N,
Jenkins S, Ingham M, An ontology for State Analysis:
Formalizing the mapping to SysML, Aerospace
Conference, 2012 IEEE.
Zeigler B P, Praehofer H & Tag G K, 2000, Theory of
modeling and simulation, Academic Press, San Diego,
California, USA.
ASimulationFidelityAssessmentFramework
471
