
CPN Based GAE Performance Prediction Framework
Sachi Nishida and Yoshiyuki Shinkawa
1
Graduate School of Science and Technology, Ryukoku University, 1-5 Seta Oe-cho Yokotani, Otsu, Shiga, Japan
Keywords:
Google App Engine, Colored Petri Net, Cloud Computing, System Performance.
Abstract:
Google App Engine (GAE) is one of the most popular PAAS type cloud platform for database transaction
systems. When we plan to run those systems on GAE, performance prediction is one of the obstacles, since
only a little performance information on GAE is available. In addition, the structure of GAE is not opened
to general public. This paper proposes a Colored Petri Net (CPN) based simulation framework, based on
the performance parameters obtained through the measurement by user written programs. The framework is
build focusing on the application structure, which consists of a series of GAE APIs, and GAE works as a
mechanism to produce the probabilistic process delay. The framework has high modularity to plug-in any
kinds of applications easily.
1 INTRODUCTION
Google App Engine (GAE) (de Jonge, 2011)(Sander-
son, 2009) is one of the most popular PAAS (Plat-
form As A Service) type cloud platform for scal-
able and economic information systems including
database transaction processing. While GAE provides
us with a easy way to implement considerably compli-
cated transaction systems with low cost, little effort,
and high quality, it seems difficult to estimate the sys-
tem performancebefore the system cutover. The main
reason is that only a little information is available on
the details of GAE, including the performance param-
eters.
This difficulty could preventthe smooth migration
of so-called mission critical transaction systems into
the GAE environment, since they usually have per-
formance and throughput constraints, and if the prob-
lems with these concerns are detected after the cu-
tover, an enormous amount of effort will be wasted
to tune-up, re-design, and re-program the system.
Therefore, the performance prediction is one of the
critical tasks for such kinds of systems to run in the
cloud.
This paper presents a simulation based approach
to predicting the performance of GAE applications.
In this approach, Colored Petri Net (CPN) (Jensen and
Kristensen, 2009) is used as a modeling and simula-
tion tool, since it provides us with a vast capability
for expressing the behavior and functionality of sys-
tems, with temporal characteristics. The rest of the
paper is organized as follows. In section 2, we in-
troduce a CPN based performance prediction frame-
work. Section 3 presents how the GAE applications
and the GAE platform are modeled using CPN, along
with the simulation data generation and resultant eval-
uation methods. Section 4 shows a way to obtain the
performance parameters using user written measure-
ment programs.
2 CPN BASED PERFORMANCE
PREDICTION FRAMEWORK
Google App Engine (GAE) is one of the most popular
cloud services, which is categorized into the PAAS.
GAE provides us with a variety of services, regard-
ing web applications, databases, and software devel-
opment environments. As a result, there could be a
variety of system forms, using different program lan-
guages and databases.
Among them, one of the typical use of GAE is
to deploy Java based Datastore applications in the
form of servlets, developed under the Eclipse with
the “Google Plugin”. GAE Datastore is one of the
NoSQL databsses (Sadalage and Fowler, 2012), with
simplified structure and manipulation, focusing more
on the availability and scalability than the integrity
and usability. The concepts of “table”, “row”, and
“column” in the relational database are approximately
mapped to “kind”, “entity”, and “property” in the
Datastore respectively. We focus on this forms of ap-
401
Nishida S. and Shinkawa Y..
CPN Based GAE Performance Prediction Framework.
DOI: 10.5220/0005106004010406
In Proceedings of the 9th International Conference on Software Engineering and Applications (ICSOFT-EA-2014), pages 401-406
ISBN: 978-989-758-036-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
plication for the performance prediction.
Since the detailed internal structure of GAE is not
opened to the general public, it seems impractical to
predict the performance based on the temporal char-
acteristics of each system component. Instead, an
application structure oriented performance prediction
seems more realistic, if we can obtain the required
time with the statistical fluctuations for each API.
These APIs include the PersistenceManager creation,
the Query object creation, the data manipulation like
data insertion, deletion, modification, and selection,
transaction control, commit/abort, and so on.
From the performanceviewpoint, each application
program is regarded as a series of these APIs, which
are passed to the GAE system. On the other hand, the
GAE system is almost a black box, although several
major components are partially opened to public, e.g.
BigTable, GFS (Google File System), and Chubby
(Chang et al., 2006) (Howard et al., 2004). There-
fore, for the performance viewpoint, it seems better
to regard GAE as a black-box mechanism to produce
a temporal delay than to model the details of it.
In order to make a performance prediction model
for GAE, we first have to choose an appropriate mod-
eling tool having the capability of
1. expressing the behavior and functionality of each
application program,
2. simulating the behavior and functionality of each
application, along with the interactions with the
GAE system, and
3. producing the temporal delay in the simulation.
Colored Petri Net (CPN) in conjunction with the CPN
tools (Jensen et al., 2007) is one of the most suitable
modeling tools for these requirements.
CPN is formally defined as a nine-tuple CPN=(P,
T, A, Σ, V, C, G, E, I) , where
P : a finite set of places.
T : a finite set of transitions.
(a transition represents an event)
A : a finite set of arcs P∩ T = P∩ A = T ∩ A =
/
0.
Σ : a finite set of non-empty color sets.
(a color represents a data type)
V : a finite set of typed variables.
C : a color function P → Σ.
G : a guard function T → expression.
(a guard controls the execution of a transition)
E : an arc expression function A → expression.
I : an initialization function : P → closed expression.
CPN itself is not furnished with the temporal ca-
pability, however it have been enhanced to the Timed
CPN (Jensen and Kristensen, 2009), by incorporat-
ing the “firing delay” concept of the timed Petri Net
(Wang, 1998) into it. In Timed CPN, each token can
optionally be assigned a timestamp property along
with a color set. By this timestamp, the firing of a
transition by this token is postponed until the times-
tamp expires.
This property is declared at the “closet” (color set)
definition time like
closet No = INT timed;
The actual timestamp is assigned by one of the three
ways, namely, by the initial token marking, by the
transaction firing, or by the arc function invocation.
The assignment operation is designated by the sym-
bol “@”, e.g. “@ + 50”.
In order to increase the modularity of the predic-
tion model, we first build a high level framework us-
ing CPN, which is composed of functionally indepen-
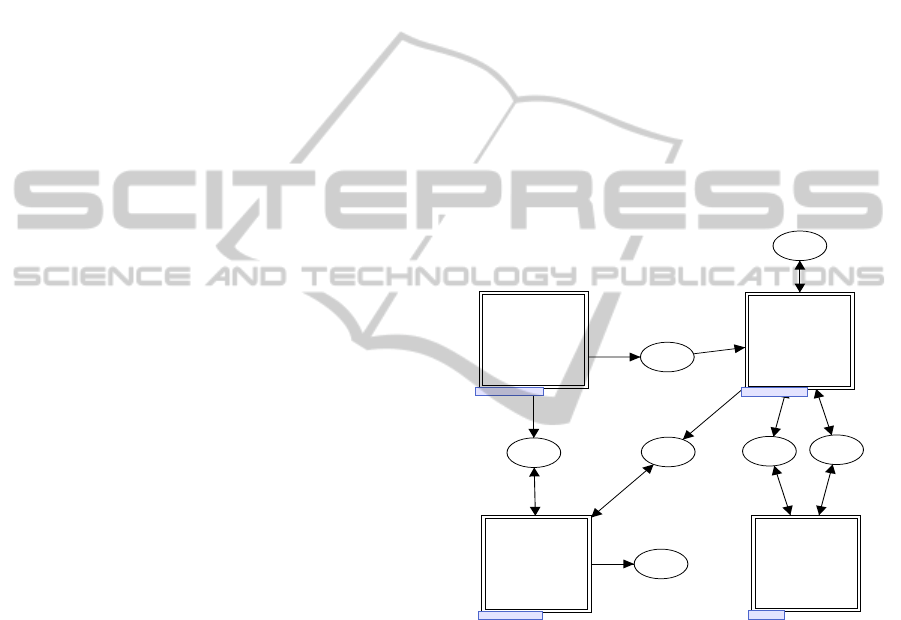
dent four major components, as shown in Figure 1. In
Application
Application
Evaluation
Evaluation
Generation
Generation
Result
CLC
OUT
SEQ
REQ
InQ
InQB
Generation
Evaluation
Application
Delay
DelayDelay
Figure 1: High Level Framework.
this figure, the “Generation” component generates all
the application programs or transactions in the form
of CPN tokens, which are to run in the GAE system.
Each token is appended an appropriate arrival time as
a CPN timestamp. The “Application” component per-
forms the execution of each application at the given
concurrency level.
The concurrency level is implemented as a max-
imum number of concurrently active threads to run
each transaction. In order to control the concurrency
level, the place “CLC” (an abbreviation for Concur-
rency Level Control) is marked with an integer list to-
ken, each element of which represent the thread avail-
ability, and the length of which represents the concur-
rency level, namely, the maximum number of concur-
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
402

rently active threads.
The “Delay” component produces the temporal
delay with statistical fluctuation. The last compo-
nent “Evaluation”examines the resultant tokens of the
simulation marked in the “OUT” place, to calculate
and report the performance indices, e.g. the mean re-
sponse time, variance, waiting time, and throughput.
3 PERFORMANCE SIMULATION
AND EVALUATION MODEL
Each component in the performance prediction
framework is refined stepwise into the more detailed
simulatable CPN model.
3.1 Refining the “Application”
Component
As stated in section 2, each application can be re-
garded as a series of GAE APIs from the performance
prediction viewpoint, since the most of execution time
is consumed for the processing of these APIs, and the
rest part would be negligibly small.
The typical GAE Datastore application, written
by Java JDO, flows as follows.
1. Handle the Session and Memcache objects in its
prologue.
2. Get the PersistenceManager instance.
3. Declare the beginning of the transaction.
4. Create and execute the Query objects to access the
Datastore as many as required.
5. Close the PersistenceManager.
6. Commit or abort the transaction.
Each action of the above process is expressed as an
“API”. For each API that interfaces the GAE system,
one CPN transition is assigned, in order to explicitly
show the sequence of the issued APIs from a trans-
action. Since this sequence is different from each
other between transactions, we have to create multi-
ple instances of this “Application” component, each
of which reflects the application logic of an individ-
ual transaction.
As shown in Figure 2, each transition in this com-
ponent is connected to the two places “REQ” and
“SEQ” that are interfaced with the “Delay” compo-
nent. The “REQ” place holds the tokens each of
which represents a single GAE API. Theses tokens
are used to produce the temporal delay by the “De-
lay” component. On the other hand, the “SEQ” place
holds a single token to control the firing sequence of
the transitions. By this token we can implement the
if-then-else branches and while loops to form the con-
trol structure of each application logic.
The color sets assigned to these places have the
same name as the places, which are defined as
closet REQ = product OP * OptList;
closet SEQ = product OP * RC * SN;
Where “OP” represents the API name, “OptList” rep-
resents the option list or argument list of the API to
derivethe accurate delay time, “RC” is the return code
from the API, and “SN” is the sequence number of the
transition to be fired next.
3.2 Refining the “Generation”
Component
The purpose of this component is to generate the
transactions to be performed in the GAE system, at
the appropriate arrival rate, following the appropriate
distribution functions.
In order to provide the transaction tokens at a de-
sired arrival rate following a desired distribution pat-
tern, we need to generate a set of the timestamps us-
ing the appropriate distribution function with the ap-
propriate mean and variance values. The CPN ML
language, which is a specification language for CPN
models, provides us with a variety of distribution
functions, e.g. Exponential, Normal, Chi-square ,
Bernoulli , and so on.
For example, in order to generate the transaction
tokens at the arrival rate 500 per second, and each in-
terval time between adjacent transactions follow the
exponential distribution function, we first define the
CPN ML function as
fun delayExp (x) = round (exponential (1.0/x));
, and add the timestamp by “@+delayExp(500.0)” to
each initial transaction token with the “timestamp =
0”. Figure 3 shows an example of “Generation” com-
ponent for this arrival rate. In this figure, “Arr” tran-
sition add the above timestamps. This “Generation”
component generates a Poisson arrival, since the time
interval between events follows the exponential distri-
bution function. The structure of “Generation” com-
ponent for another transaction arrival pattern is basi-
cally the same. The generated transaction tokens are
marked in the “InQ” place, which interfaces with the
“Application” component. The “InQB” place holds
the copy of all the generated transaction tokens for
the later performance evaluation.
CPNBasedGAEPerformancePredictionFramework
403

API4
API3
API2API1
SEQ
REQ
Out
CTC
InQ
Delay
DelayDelay
Figure 2: “Application” Component.
3.3 Refining the “Delay” Component
The functionality of this component is rather simple
in comparison with other components, since it simply
adds the temporal delay to the received tokens which
represents the GAE APIs. However, the delay could
vary with many factors, some of which we cannot
even forecast, e.g. the system reconfiguration, data
replication, or recovery operations. Therefore, this
component calculates the delay based on the mean
and the variance values obtained through the system
measurement. This approach is discussed in the next
section.
Assuming this information is obtained, the com-
ponent is implemented as a CPN model as shown
in Figure 4. In this figure, each transition “API-x”
(x = A, B, ··· ) represents a specific API. The delay
would be different even for the same API, depending
on the characteristics of the object to be handled and
the API options such as setFilter options. Such in-
formation is embedded into the “OptList” field of the
token “REQ” by the “Application” component, and
is handled by the CPN ML functions in the “Delay”
component. For example, if the delay of data insertion
varies with the kinds of the Datastore, following the
normal distribution functions with the different mean
and variance values, we have to define the CPN ML
function for the delay as
fun delayInsert kind = case kind of
1 => round(normal(250.0,150.0)) |
2 => round(normal(200.0, 95.0)) |
3 => round(normal(350.0, 150.0)) |
=> 0;
This CPN ML function generates the different delay
patterns for three different Datastore kinds, each of
which follows the normal distribution function with
different mean and variance values.
The transition “API-x” works a server in terms
of queuing theory (Gnedenko and Kovalenko, 1989),
therefore it should cease the firing while it processes
the received request. It means if the transition gener-
ates the delay t, it never fires until the time t expires.
On the other hand, the Timed CPN adopts a different
mechanism. Even though the timestamp of a token
postpones the firing of a transition, the firing ends in-
stantaneously, and another token can fire it. In order
to avoid this conflict, we use one more place “Px” for
each transition “API-x” as shown in Figure 4. The to-
ken in this place is initially marked with “timestamp
= 0”. Each time “API-x” fires, the timestamp value
of the token in “Px” is increased by the delay time.
Therefore, the token ceases the firing of “API-x” for
the delay time.
3.4 Refining the “Evaluation”
Component
After the simulation of the “Application” components
ends, interacting with the “Delay” component, the
“OUT” place contains all the scheduled transaction
tokens with their end timestamps. Since the copy of
the arrival transaction tokens with their arrival times-
tamps are marked in the “InQB” place, this module
can calculate the elapsed time for each transaction,
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
404

n-1
tran
n
genTran 5 10 6
trantran
Application
Application
Arr
@+delayExp(500.0)
[n>1]
Out
TRAN
InQB
TRAN
Con
10
INT
InQ
TRAN
In
(1, [(1,1),(1,2),(2,3),(2,4),(1,4)])
TRAN
Application
CLC
SEQREQ
Figure 3: “Generation” Component.
x
x
r
delayAPIA r
API-EAPI-DAPI-C
API-BAPI-A
@+delayAPIA r
PEPDPCPBPA
SEQ
REQ
Application
ApplicationApplication
Figure 4: “Delay” Component.
along with the mean response time, the variance, and
the throughput. Each elapsed time is calculated by
subtracting the arrival timestamp from the end times-
tamp, the mean response time is obtained by divid-
ing the summation of these elapsed times by the num-
ber of transactions, and the variance is derived from
this mean response time and each response time. The
throughput is a number of the processed transactions
per time unit, and is calculated similarly.
The resultant performance data obtained through
the simulation are marked in the “Result” place as a
report.
4 MEASURING AND
ESTIMATING THE BASE
PARAMETERS
The proposed framework regards the GAE as a black-
box, therefore we need to obtain the base performance
parameters, e.g. the mean and variance values of the
elapsed time of each API, by measuring the system.
For the obtainment of these parameters, a set of sim-
ple Java programs is used in this framework. Since
an elapsed time of each API is usually too short to be
measured by a program, each measurement program
issues several hundreds of the same API, and calcu-
CPNBasedGAEPerformancePredictionFramework
405

lates the mean value. This mean value is written to
the GAE log as a warning. Figure 5 shows an exam-
ple of such a Java code.
Each measurement program is performed many
times to obtain the variance and to estimate the proper
distribution function. As for the Datastore access
APIs, the elapsed time would vary with the size of the
kind and the number of the propertiess in the kind.
Therefore, we have to measure the parameters vary-
ing these factors. Table 1 shows a sample result of
such a measurement. All the obtained parameters are
Query query = pm. newQuery ( Buch20 . cl as s ) ;
long s t a r t = System . cu rren tTi meM illi s () ;
for ( in t i = 1; i <=200; i ++){
St r i n g s = ” bookId ==\”” + i + ” \” ” ;
query . s e t F i l t e r ( s ) ;
r t . s e t F i l t e r ( f i l t e r ) ;
bookList = ( L is t<Buch20>)query . execute ( ) ;
}
long st o p = System . cur rent Tim eMi llis ( ) ;
long t = s top − s t a r t ;
log . warning ( ” Elapse d Time = ” + t /2 00) ;
Figure 5: Measurement Program Example.
embedded into the “Delay” component to produce the
appropriate delay.
Table 1: Mean Value – Elapsed Time.
Size Sel Mod Del Ins
3 × 10000 3.54 94.34 73.13 77.03
5 × 8000 2.74 90.65 71.70 64.04
10 × 4000 3.99 48.38 94.99 96.90
20 × 2000 2.80 101.38 80.80 64.67
50 × 1000 2.69 76.09 62.80 105.57
Since the above performanceparameters vary over
time, or in other words, they are time varying fac-
tors, we have to measure them periodically, and re-
flect them in the “Delay” component in order to keep
the prediction framework up to date.
5 CONCLUSIONS
A simulation based performance prediction frame-
work for GAE is proposed, which uses the Timed Col-
ored Petri Net (Timed CPN). In order to increase the
modularity, the framework is composed of four func-
tionally independent components connected together
by CPN places, namely, “Generation”, “Application”,
“Delay” and “Evaluation” components.
Since GAE is almost a black-box from the per-
formance prediction viewpoint, most performancepa-
rameters have to be obtained through the measure-
ment using user written programs. Using the obtained
parameters, that is, the mean and variance values with
the estimated distribution functions, “Delay” compo-
nents produces the delay for each API, then add it to
the timestamp attribute of each token that has issued
the API.
At the end of the simulation, the “Evaluation”
component examines the resultant tokens to calculate
the performance indices. The performance parame-
ters change over time, or they are the time-varying
factors, therefore the above measurement must be
done periodically,so that the latest parameters are em-
bedded into the “Delay” component.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number 25330094.
REFERENCES
Chang, F., Dean, J., Ghemawat, S., Hsieh, W. C., Wallach,
D. A., Burrows, M., Chandra, T., Fikes, A., and Gru-
ber, R. E. (2006). Bigtable: A Distributed Storage
System for Structured Data. In Proc. the 7th Con-
ference on USENIX Symposium on Operating Systems
Design and Implementation - Volume 7, pages 205–
218.
de Jonge, A. (2011). Essential App Engine: Building
High-Performance Java Apps with Google App En-
gine. Addison-Wesley Professional.
Gnedenko, B. V. and Kovalenko, I. N. (1989). Intro-
duction to Queuing Theory (Mathematical Modeling).
Birkhaeuser Boston.
Howard, S. G., Gobioff, H., and Leung, S. (2004). The
Google File System.
Jensen, K. and Kristensen, L. (2009). Coloured Petri
Nets: Modeling and Validation of Concurrent Sys-
tems. Springer-Verlag.
Jensen, K., Kristensen, L. M., and Wells, L. (2007).
Coloured Petri Nets and CPN Tools for Modelling
and Validation of Concurrent Systems. In Inter-
national Journal on Software Tools for Technology
Transfer (STTT) Volume 9, Numbers 3-4, pages 213–
254. Springer-Verlag.
Sadalage, P. J. and Fowler, M. (2012). NoSQL Distilled: A
Brief Guide to the Emerging World of Polyglot Persis-
tence. Addison-Wesley Professional.
Sanderson, D. (2009). Programming Google App Engine.
Oreilly & Associates Inc.
Wang, J. (1998). Timed Petri Nets: Theory and Application
(The International Series on Discrete Event Dynamic
Systems). Springer.
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
406
