
Pricing Schemes for Metropolitan Traffic Data Markets
Negin Golrezaei and Hamid Nazerzadeh
Marshall School of Business, University of Southern California, Los Angeles, CA 90089, U.S.A.
Keywords:
Data Markets, Traffic Sensors Data, Pricing Schemes, Mixed Duopoly.
Abstract:
Data marketplaces provide platforms for management of large data sets. The data markets are rapidly growing,
yet the pricing strategies for data and data analytics are not yet well-understood. In this paper, we explore
some of the pricing schemes applicable to data marketplaces in the context of transportation traffic data. This
includes historical and real-time freeway and arterial congestion data. We investigate pricing raw sensor data
vs. processed information (e.g, prediction of traffic patterns or route planning services) and show that, under
natural assumptions, the raw data should be priced higher than processed information.
1 INTRODUCTION
Big data marketplaces, such as Microsoft Azure
1
and
Infochimps
2
are rapidly growing (Furrier, 2012; Lohr,
2011). These data marketplaces offer a platform for
data providers to upload and store their data as well as
to share with and sell their data to their clients. Un-
like more established online market such as Internet
advertising and cloud computing, data marketplaces
are still experimenting with difference pricing strate-
gies (Schomm et al., 2013; Muschalle et al., 2013).
In this paper, we investigate the pricing aspects of de-
signing data marketplaces with focus on traffic data.
Traffic congestion is a growing problem in many
metropolitan areas. It not only wastes our time and
energy, but also increases air pollution. According to
Texas Transportation Institute, the number of hours
wasted in traffic is increased by more than 500% be-
tween 1982 and 2005. Fortunately, a study by McK-
insey Global Institute shows that by 2020 traffic data
can avoid traffic congestion and save users by $600
billion per year (Lohr, 2011).
Most major cities collect real-time traffic flow (ve-
hicles’ volume and speed), congestion, and accidents’
data on freeways and arterial.
3
This data is mainly
used to obtained predictions of the traffic patterns and
for route planning, especially for emergency services
such as police and ambulances. This data is also
commercially used by Google, Microsoft, and Ap-
1
http://datamarket.azure.com/browse/data
2
http://www.infochimps.com/
3
For instance, see http://www.cattlab.umd.edu/
?portfolio=ritis.
ple maps’ services, among many other companies,
that create value for their customers by shortening
their travel time via providing congestion-aware route
planning services (integrated with the GPS and turn-
by-turn navigate systems).
Currently, in most countries (including the United
States), the traffic data is provided for free to for-
porfit companies. Due to the success of the com-
mercial services that use the real-time traffic informa-
tion, several cities are considering generating revenue
from the traffic data that is shared with the for-profit
companies. For instance, the Los Angeles County
Metropolitan Transportation Authority, has sponsored
the Regional Integration of Intelligent Transportation
Systems (RIITS)
4
network with the goal of col-
lecting and storing traffic data and creating a sys-
tem that enables the use of stored data for trans-
portation applications. We will refer to this system
as Archived Data Management System (ADMS); see
also (ADMS, 2009). In addition to real-time infor-
mation, historical traffic data can be utilized to better
predict traffic congestion (Demiryurek et al., 2011).
5
In this paper, we consider an abstraction of such
environments where data provider offers a “service”
at a certain quality. We think of the service, as pro-
cessed information. Namely, the traffic data is pro-
cessed to offer a prediction of the traffic patterns or
4
http://www.riits.net/.
5
(Pan et al., 2012) show that due to a strong temporal
correlation present in traffic data, accuracy of traffic pre-
diction can be improved by more than 60% using historical
data. see also (Yuan et al., 2011), (Gehrke and Wojtusiak,
2008), (Williams et al., 1998), and (Park et al., 1998).
266
Golrezaei N. and Nazerzadeh H..
Pricing Schemes for Metropolitan Traffic Data Markets.
DOI: 10.5220/0005106602660271
In Proceedings of 3rd International Conference on Data Management Technologies and Applications (DATA-2014), pages 266-271
ISBN: 978-989-758-035-2
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

congestion. Another example could be congestion-
aware route planning services. Our analysis high-
lights the role of the quality of the provided service.
If the service is prediction of the traffic patterns, then
the quality corresponds to the accuracy and reliability
of the estimates, e.g., travel time. In the context of
route planning, the quality corresponds to the differ-
ence of the travel time compared with the “optimal”
travel time (ideally, the service would find the path
with the shortest travel time taking into account the
current and future congestion).
The quality of processed information is deter-
mined by quality and resolution of raw data and more
importantly by the quality and precision of analysis
and processes performed on raw data.
6
Naturally, in
our model, providing higher quality service would be
more costly.
We consider an environment with heterogeneous
customers that are differentiated with respect to their
“delay-sensitivity”. In other words, a customer of
“higher type” are more time sensitive and would pre-
fer a higher quality service.
As the first step towards understanding pricing
structures in such data markets, we compare the price
of processed information (service) vs. raw data. At
the first glance, it might seem that processed infor-
mation should be priced higher since it costs more.
However, we show that the opposite is true.
We consider a monopoly market that consists of a
data provider who sells raw data and processed infor-
mation at a certain quality level to a continuum mass
of customers. Any customers who is not satisfied with
the quality of processed information can purchase raw
data and then investing in obtaining higher quality in-
formation. Raw data which has not been subjected
to processing or any other manipulations has the po-
tential to become “information”, but, it requires effort
and cost. The intuition is that customers (companies)
of “higher type”’, would purchase raw data and in-
vest in obtaining better (more accurate) predictions of
traffic patterns and travel times.
Customers’ decisions on whether or not to buy
raw data or processed information depend on their
valuations and the cost of processing raw data, as
well as price of raw data and processed information.
We show that customers with higher valuations have
higher perceived value for raw data. Thus, they are
willing to purchase raw data rather than processed
information. The data provider, in turn, reacts to
6
Raw data is usually collected by sensor devices that are
installed in the roads. Several researchers have studied sen-
sor architectures and its impact on quality and resolution of
raw data; see e.g., (Knaian, 2000), (Tubaishat et al., 2009),
and (Klein, 2001).
this observation and sets higher price for raw data
compare with processed information.
7
Using this
scheme, the data provider obtains a higher profit.
As a next step, we seek to understand how the
pricing scheme changes when the data provider com-
petes with other firms.
Considering competition is partly motivated by
the aforementioned RIITS project and potentials for
public-private partnership. One possibility is to sell
raw data to private firms. The private firms add value
to raw data and at the same time offset the opera-
tional cost of the project. In this situation, RIITS and
private firms that sell processed information become
competitors in a mixed market.
8
We consider a market that consists of a data
provider and a private firm. The data provider sells
raw data to the private firm. The data provider and pri-
vate firm process raw data possibly at different qual-
ity levels and sell processed information to customers.
Then, they compete with each other in a vertically dif-
ferentiated mixed duopoly market. The goal is to ob-
tain insights with regards to the endogenous quality
and price choice in this market. Based on our prelim-
inary analysis, we conjecture that value-based pricing
scheme is still optimal for this market. That is, raw
data that has not undergone costly processes would
be priced higher than processed information.
We also consider a variation of the mixed duopoly
market in which the data provider has to offer his pro-
cessed information for free. We showthat when a data
provider offers free processed information, the private
firm should respond by decreasing his quality.
Organization. In Section 2, we look at the
monopoly market. We discuss the mixed duopoly
market Section 3. We conclude this paper in Section
4 with a discussion on future research directions.
2 MONOPOLY MARKET
We consider a market of size m with a monopoly data
provider. The data provider sells processed informa-
tion with quality q at price P
q
. As discussed in the
7
As mentioned before, this is rather surprising consid-
ering the extra processing cost that the data provide incurs
for processed information. Such a pricing scheme is called
value-based pricing since it is based on the perceived value
rather than the cost structure (cf. (Harmon et al., 2009) and
(Shapiro et al., 1999)).
8
Note that the mixed market is referred to a market
consists of public and private firms (Delbono, 1991) and
(Ishibashi and Kaneko, 2008).
PricingSchemesforMetropolitanTrafficDataMarkets
267

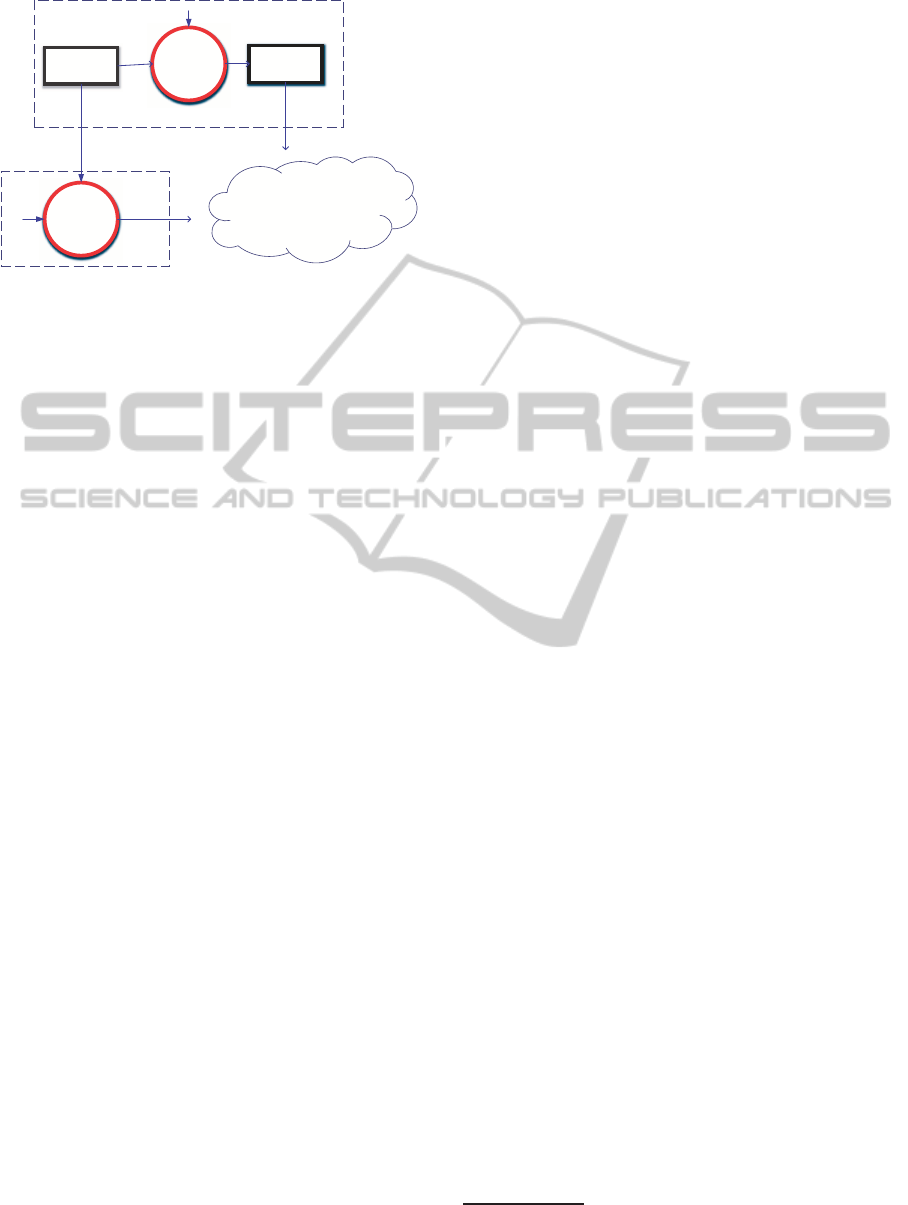
!"#$%"&"
'()*+,,-./$
'()*+,,+0$
%"&"
'
(
'
1
1
2"(3+&
Figure 1: Monopoly Market.
previous section, one can think of quality as the ac-
curacy of the predictions of the traffic patterns and
congestions. The cost of processing data for the data
provider at quality q is c
1
(q).
The data provide also sells raw data at price P
r
;
see the model in Figure 1.
Each customer has a type θ which represents the
delay sensitivity of the customer. A higher θ implies
higher value for time, e.g, a stronger preference on
choosing the shortest path. We assume that θ is in-
dependent across customers and is drawn from a dis-
tribution F.
9
The valuation of a customer with type
θ for processed information with quality q is v(q, θ),
where v is increasing in q and θ.
Customers can either purchase raw data or pro-
cessed information. When a customer with type θ
purchases processed information with quality q at
price P
q
, his net utility is given by
v(θ, q) − P
q
We make the following assumption about the val-
uation function v(θ, q).
Assumption 1. For any q
2
≥ q
1
and θ
2
≥ θ
1
, the val-
uation function satisfies the following increasing dif-
ferences property:
v(θ
2
, q
1
) − v(θ
1
, q
1
) ≤ v(θ
2
, q
2
) − v(θ
1
, q
2
)
This assumption implies that the marginal incre-
ment of valuation function is an increasing function
of quality. Similar increasing differences assumptions
are quite common in the game theory and the equilib-
rium analysis literature; see (Levin, 2003).
9
This is a standard assumption in the economics and
pricing literature.
Each customer who purchases raw data can pro-
cess to obtain information at some quality level.
10
We assume that cost of processing raw data for cus-
tomers at quality level q is c
2
(q). Thus, a customer
with type θ who purchases raw data processes it at
quality q
θ
r
≥ q, where q
θ
r
solves the following opti-
mization problem.
q
θ
r
= argmax
a≥q
{v(θ, a) − c
2
(a)}.
Thus, the net utility of a customer with type θ who
purchases raw data at price P
r
is given by
v(θ, q
θ
r
) − P
r
− c
2
(q
θ
r
).
Optimal Prices and Quality
We now look at how the data provider determines his
prices P
q
and P
r
, and quality q. We start with the fol-
lowing proposition.
Proposition 2.1. There exists threshed θ
r
such that
only customers with type greater than θ
r
purchase
raw data.
The proof is given in the appendix. According to
Proposition 2.1, high type customers will purchase
raw data and low type customers will purchase pro-
cessed information. Then, a customer with type θ
r
is indifferent between purchasing raw data and pro-
cessed information, where θ
r
satisfies the following
equation.
max
q
{v(θ
r
, q) − c
2
(q)} − P
r
= v(θ
r
, q) − P
q
v(θ
r
, q
θ
r
r
) − c
2
(q
θ
r
r
) − P
r
= v(θ
r
, q) − v(θ
q
, q) (1)
Similarly, for a given quality q and price P
q
, cus-
tomers with type θ
q
is indifferent between purchas-
ing processed information and not purchasing at all,
where θ
q
solves
v(θ
q
, q) − P
q
= 0.
That is, P
q
= v(θ
q
, q).
The data provider chooses P
r
, P
q
, and q to maxi-
mize his profit, which can be written as follows
π = mP
q
(F(θ
r
) − F(θ
q
)) − c
1
(q) + mP
r
(1− F(θ
r
)),
where m is the market size. The sum of the first and
second terms is profit of processed information and
the last term is profit of raw data.
10
These customers only need processed information for
their private uses. In Section 3, we consider the case where
a private firm purchases raw data, processes it, and sell it to
customers.
DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications
268
!"#$%"&"
'()*+,,-./$
'()*+,,+0$
%"&"
'
(
'
1
2
1
3"(4+&
'()*+,,-./$
'
5
2
5
%"&"$'()6-0+(
!-6"7
Figure 2: Duopoly Market.
The following proposition compares P
r
and P
q
in
the optimal solution.
Surprisingly, although the data
provider incurs an additional cost for processed infor-
mation, he sets a lower price for it.
Proposition 2.2. In the optimal solution, we have
P
r
≥ P
q
.
The proof is given in the appendix. In the proof
we use that fact that high valuation customers have
higher perceived value for raw data.
3 MIXED DUOPOLY MARKET
In the previous section, we assume that customers
who purchase raw data, only use it for their private
uses. Here, we consider the case that customers who
purchaseraw data, process it, and sell processed infor-
mation to other customers. More precisely, we con-
sider a duopoly market consists of a data provider and
a private firm. The data providersells raw data at price
P
r
to the private firm. The private firm processes the
data and sells it to the customers. We assume that
the data provider and the private firm compete with
each other in a vertically differentiated duopoly mar-
ket. That is, they sell processed information to cus-
tomers at different qualities and prices. Without loss
of generality, we assume that the private firm sells
processed information with a higher quality than the
data provider.
Figure 2 illustrates the model. In the figure q
1
and
q
2
are respectively quality of processed information
for the data provider and the private firm. Further-
more, the data provider and the private firm sell pro-
cessed information at price P
1
and P
2
, respectively.
Finally, P
r
is the price that the private firm pays for
raw data.
Since in context of traffic data, the data provider
is a public firm, we consider a more general model
in which the data provider maximizes a convex com-
bination of his profit and social welfare, i.e., βW +
(1− β)π
1
, where β ∈ [0, 1] and W is social welfare.
11
When the data provider wants to maximize his profit,
he sets β to zero. However, counterintuitively, we
show that due to the game between the data provider
and the private firm, social welfare is not maximized
at β = 1. In other words, the data provider should con-
sider his profit is his objective function. Otherwise he
cannot yield the highest social welfare.
In the following, we summarize the timing of the
game between the data provider and private firm.
1- The data provider decides about his objective
function or more precisely parameter β ∈ [0, 1].
2- The data provider sells raw data at price P
r
to the
private firm. The private firm can choose not to
buy the raw data.
3- The data provider and the private firm simultane-
ously make a decision about quality of their ser-
vices.
4- After the quality levels are realized, both firm de-
termine their prices.
For this game we explicitly analyze the endoge-
nous quality and price choice in a backward manner.
Precisely, we first establish the pricing strategy of the
firms, and then we find their quality strategies. Due to
the space limit, in the following we only summarize
our finding.
Pricing Strategies. Our preliminary analysis show
that the data provider increases his price when the
private firm does and vice versa. Furthermore, the
private firm increases his price when he improves his
quality, and he reacts with a lower price when the data
provider offers a higher quality. However, the data
provider does not always increase his price when he
improves his quality. He raises his price when there
is enough gap between his offered quality and quality
of the private firm. We further conjecture that price of
raw data is higher than price of processed information
as long as the market size is large enough.
Quality Strategies. The private firm reacts with a
higher quality against an increase in quality of the
data provider. But, in some cases, when the private
firm improveshis quality, the data provideris not will-
ing to increase his quality. This encourages customers
to purchase higher quality data from the private firm.
Our preliminary results show that the quality of the
data provider and private firm is increasing in β.
11
The social welfare is the sum of surplus of customers
and both firms.
PricingSchemesforMetropolitanTrafficDataMarkets
269

Free Data. We also investigate the case, where the
data provider offers processed information for free –
this is similar to the current practice where the real-
time traffic information is offered at no cost. Inter-
estingly, in that case, the private firm has less incen-
tive to increase his quality. In other words, the pri-
vate firm provides lower quality compare to the case
that the data provider prices his data. This, in turn,
decreases social welfare. We conjecture that with
free processed information, the data provider needs
to ignore his profit to maximize social welfare. Pre-
cisely, when the data provider does not price his data,
welfare-maximizing β is exactly one.
4 FUTURE DIRECTIONS
In addition to completing our analysis for the afore-
mentioned monopoly and duopoly, we would like to
study other pricing strategies in data markets. A
natural future step is to compare subscription and
consumption-based pricing schemes similar to those
currently used in cloud computing, for instance by
Amazon’s EC2 platform.
12
In a consumption-based
pricing model, customers pay according to the re-
sources used. The resource can be the amount of data
they acquire. However, in subscription-based pricing
models, customers commit to the service for specified
periods of time and pay a flat fee for that period.
ACKNOWLEDGEMENTS
We would like to thank Cyrus Shahabi and Ugur
Demiryurek for inspiring discussions. This work is
supported by a grant from Integrated Media System
Center at USC.
REFERENCES
ADMS (2009). Adms smart travel lab. Available at
http://cts.virginia.edu/stl-adms.htm/.
Delbono, F. (1991). Quality choice in a vertically differeiti-
ated mixed duopo1y.
Demiryurek, U., Banaei-Kashani, F., Shahabi, C., and Ran-
ganathan, A. (2011). Online computation of fastest
path in time-dependent spatial networks. In Advances
in Spatial and Temporal Databases, pages 92–111.
Springer.
Furrier, J. (2012). Big data is creating the future - it’s a $50
billion market. Forbes.
12
http://aws.amazon.com/ec2/pricing/.
Gehrke, J. D. and Wojtusiak, J. (2008). Traffic prediction
for agent route planning. In Computational Science–
ICCS 2008, pages 692–701. Springer.
Harmon, R., Demirkan, H., Hefley, B., and Auseklis, N.
(2009). Pricing strategies for information technology
services: A value-based approach. In System Sciences,
2009. HICSS’09. 42nd Hawaii International Confer-
ence on, pages 1–10. IEEE.
Ishibashi, K. and Kaneko, T. (2008). Partial privatization
in mixed duopoly with price and quality competition.
Journal of Economics, 95(3):213–231.
Klein, L. A. (2001). Sensor technologies and data require-
ments for ITS.
Knaian, A. N. (2000). A wireless sensor network for smart
roadbeds and intelligent transportation systems. PhD
thesis, Massachusetts Institute of Technology.
Levin, J. (2003). Supermodular games. Lectures Notes,
Department of Economics, Stanford University.
Lohr, S. (2011). New ways to exploit raw data may bring
surge of innovation, a study says. The New York Times.
Available at http://www.nytimes.com/2011/05/13/
technology/13data.html.
Muschalle, A., Stahl, F., L¨oser, A., and Vossen, G.
(2013). Pricing approaches for data markets. In En-
abling Real-Time Business Intelligence, pages 129–
144. Springer.
Pan, B., Demiryurek, U., and Shahabi, C. (2012). Utiliz-
ing real-world transportation data for accurate traffic
prediction. In ICDM, pages 595–604.
Park, B., Messer, C. J., and Urbanik II, T. (1998). Short-
term freeway traffic volume forecasting using radial
basis function neural network. Transportation Re-
search Record: Journal of the Transportation Re-
search Board, 1651(1):39–47.
Schomm, F., Stahl, F., and Vossen, G. (2013). Marketplaces
for data: an initial survey. ACM SIGMOD Record,
42(1):15–26.
Shapiro, C., Varian, H. R., and Becker, W. (1999). Informa-
tion rules: a strategic guide to the network economy.
Journal of Economic Education, 30:189–190.
Tubaishat, M., Zhuang, P., Qi, Q., and Shang, Y. (2009).
Wireless sensor networks in intelligent transportation
systems. Wireless communications and mobile com-
puting, 9(3):287–302.
Williams, B. M., Durvasula, P. K., and Brown, D. E. (1998).
Urban freeway traffic flow prediction: application
of seasonal autoregressive integrated moving average
and exponential smoothing models. Transportation
Research Record: Journal of the Transportation Re-
search Board, 1644(1):132–141.
Yuan, J., Zheng, Y., Xie, X., and Sun, G. (2011). Driving
with knowledge from the physical world. In Proceed-
ings of the 17th ACM SIGKDD international confer-
ence on Knowledge discovery and data mining, pages
316–324. ACM.
DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications
270

APPENDIX
Proof of Proposition 2.1. We show that if a customer
with type θ
1
purchases raw data, then any customers
with higher types would also buy raw data.
Since a customer with type θ
1
prefers to purchase
raw data rather than processed information, we have
max
a≥q
{v(θ
1
, a) − c
2
(a)} − P
r
≥ v(θ
1
, q) − P
q
v(θ
1
, q
θ
1
r
) − c
2
(q
θ
1
r
) − v(θ
1
, q) ≥ P
r
− P
q
By Assumption 1, for any θ
2
> θ
1
, we have
v(θ
1
, q
θ
1
r
) − v(θ
1
, q) ≤ v(θ
2
, q
θ
1
r
) − v(θ
2
, q)
Therefore,
v(θ
2
, q
θ
1
r
) − c
2
(q
θ
1
r
) − v(θ
2
, q) ≥ P
r
− P
q
Considering the fact that
v(θ
2
, q
θ
1
r
) − c
2
(q
θ
1
r
) ≤ max
a≥q
{v(θ
2
, a) − c
2
(a)},
we obtain
max
a≥q
{v(θ
2
, a) − c
2
(a)} − v(θ
2
, q) ≥ P
r
− P
q
,
which is the desired result.
Proof of Proposition 2.2. By Eq. (1), the price of raw
data is max
a≥q
{v(θ
r
, a) − c(a)} + v(θ
q
, q) − v(θ
r
, q).
Then, the profit of the data provider can be written as
π = m
F(θ
r
) − F(θ
q
)
× v(θ
q
, q) − c
1
(q)
+ m
1− F(θ
r
)
×
max
a≥q
{v(θ
r
, a) − c(a)} + v(θ
q
, q) − v(θ
r
, q)
Note that profit of the data provider is a function of
θ
r
, θ
q
, and q. Assume that the data provider has al-
ready decided about q and θ
q
. Then, he is sure that at
least m× (1− F(θ
q
)) customers are willing to pay for
processed information if θ
r
is chosen so large that no
customer considers buying raw data. In that case, he
would earn
m(1− F(θ
q
))v(θ
q
, q)
Therefore, having customers who purchase raw data
is beneficial for the data provider if
m
F(θ
r
) − F(θ
q
)
× v(θ
q
, q) − c(q) + m
1− F(θ
r
)
×
max
a≥q
{v(θ
r
, a) − c(a)} + v(θ
q
, q) − v(θ
r
, q)
≥ m× (1− F(θ
q
)) × v(θ
q
, q) − c(q)
or equivalently
max
a≥q
{v(θ
r
, a)−c(a)}+v(θ
q
, q)−
v(θ
r
, q)
≥ v(θ
q
, q). Considering the fact that the left
hand side is P
r
and the right hand side is P
q
, the proof
is complete.
PricingSchemesforMetropolitanTrafficDataMarkets
271
