Chive: A Simulation Tool for Epidemic Data Replication Protocols

Benchmarking

A. Jim´enez-Y´a˜nez

, J. Navarro

, F. D. Mu˜noz-Esco´ı

, I. Arrieta-Salinas

and J. E. Armend´ariz-I˜nigo

Dpto. Ingenier´ıa Matem´atica e Inform´atica, Universidad P´ublica de Navarra, 31006 Pamplona, Spain

Internet Technologies and Storage Research Group, La Salle - Ramon Llull University, 08022 Barcelona, Spain

Instituto Tecnol´ogico de Inform´atica, Univ. Polit`ecnica de Val`encia, 46022 Valencia, Spain

Keywords:

Scalable Datastore, Epidemic Data Replication, Performance Evaluation, Consistency.

Abstract:

Epidemic data replication protocols are an interesting approach to address the scalability limitations of classic

distributed databases. However, devising a system layout that takes full advantage of epidemic replication

is a challenging task due to the high number of associated conﬁguration parameters (e.g., replication layers,

number of replicas per layer, etc.). The purpose of this paper is to present a Java-based simulation tool that

simulates the execution of epidemic data replication protocols on user-deﬁned conﬁgurations under different

workloads. Conducted experiments show that by using the proposed approach (1) the internal dynamics of

epidemic data replication protocols under a speciﬁc scenario are better understood, (2) the distributed database

system design process is considerably speeded up, and (3) different system conﬁgurations can be rapidly

prototyped.

1 INTRODUCTION

Epidemic data replication protocols (Eugster et al.,

2004) have emerged as an appealing alternative to ad-

dress the scalability limitations posed by current ap-

plications that (1) deal with vast amounts of data and

(2) cannot shift to the NoSQL paradigm (Stonebraker,

2010) due to their intrinsically transactional nature

(Navarro et al., 2011). These protocols organize sys-

tem replicas into a set of tiers following a tree struc-

ture in which the root tier is the ﬁrst to receive client

updates and forwards them to its children, which re-

cursively propagate updates to the lower tiers until

reaching the last tier. As a result, updates are im-

plicitly sequentially ordered along the tree: the root

tier has the most recent data (also referred to as fresh

data), whereas lower levels own older data (also re-

ferred to as stale data). Consequently, clients can se-

lect the most suitable tier to retrieve data according to

the application freshness constraints.

Indeed, reducing the number of replicas on which

clients can perform update operations—the ones that

greatly limit the system scalability—and later prop-

agating changes to an arbitrarily large number of

servers, may bring important features to the data store

such as variable consistency, adaptive load balancing,

elasticity, or system reconﬁguration (Arrieta-Salinas

et al., 2012).

Despite the fact that these protocols have been

widely analyzed on the literature from a theoretical

point of view, it is still a challenge for system archi-

tects and practitioners to deploy them in real-world

scenarios. Speciﬁcally, it is fairly complex to ﬁnd

out the optimal system conﬁguration (e.g., number

of replicas that accept update operations, number of

replicas on the ﬁrst replication tier etc.) that takes full

advantage from the data epidemic replication protocol

to maximize system throughput. In fact, the lack of

tools that forecast the system behavior (e.g., analyti-

cal models or simulation environments) when running

this kind of protocols on different scenarios, drives

practitioners to conduct trial and error experiments to

come up with an acceptable architecture layout. How-

ever,when facing large-scale problems this methodol-

ogy becomes time consuming and, thus, unfeasible.

As statistically modeling workloads and system

resources results into too restrictive solutions, the pur-

pose of this paper is to present Chive: a custom

Java-based simulation environment speciﬁcally con-

ceived to assist system architects in the design pro-

cess of a system architecture that runs an epidemic

data replication protocol. Additionally, we present

428

Jiménez-Yáñez A., Navarro J., Muñoz-Escoí F., Arrieta-Salinas I. and Armendáriz-Iñigo J..

Chive: A Simulation Tool for Epidemic Data Replication Protocols Benchmarking.

DOI: 10.5220/0005107004280436

In Proceedings of the 9th International Conference on Software Engineering and Applications (ICSOFT-EA-2014), pages 428-436

ISBN: 978-989-758-036-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

a set of metrics on the simulator to assess and com-

pare the performance of every simulation run. To

support our proposal, we have simulated three differ-

ent epidemic data replication strategies and analyzed

the obtained results. Conducted experiments show

the beneﬁts of this tool and encourage practitioners to

work in this direction. Obtained results might be used

to complement machine-learning based approaches

aimed to ﬁnd out the optimal system conﬁguration for

ever-changing workloads (aka data streams) (Sancho-

Asensio et al., 2014).

The remainder of this paper is organized as fol-

lows. Section 2 elaborates on the related work. Sec-

tion 3 describes the system model used to build the

simulator and discusses its correctness criterion. Sec-

tion 4 provides the implementation details of the pro-

posed simulator. Section 5 presents the conducted ex-

periments. Finally, Section 6 summarizes the conclu-

sions of this work and outlines some future research

directions.

2 RELATED WORK

Designing scalable data replication protocols in dis-

tributed database has been a hot research topic during

the last 30 years. In the decade of the 80s two op-

posite proposals were made: shared-nothing (Stone-

braker, 1986) (or database partitioning / sharding) and

shared-data (Shoens, 1986) (aka shared-everything).

The former is able to enhance overall performance

when most transactions only need to access the data

stored in a single shard, whilst the latter is able to

manage in each node transactions that access to large

datasets, assuming that conﬂicts among concurrent

transactions are rare. Several recent papers have

shown that both models are functionally equivalent

(Johnson et al., 2014).

The main objective in order to obtain high scala-

bility is to avoid any contention focus. To this end,

(Johnson et al., 2014) identiﬁes “unscalable commu-

nication” as one that has an unbounded number of

occurrences in the life of any transaction. This un-

scalable communication is mainly generated by the

critical sections managed by the locking and logging

subsystems in a distributed DBMS. A perfect parti-

tioning criterion may avoid unscalable communica-

tion, although it is difﬁcult to achieve it in practice

(Sancho-Asensio et al., 2014).

Systems that pretend to be scalable are usually de-

ployed in multiple datacenters. In those scenarios a

trade-off between consistency, availability and net-

work disconnection arises (also known as the CAP

theorem (Gilbert and Lynch, 2002)). Such problem

was identiﬁed in the ﬁeld of distributed databases in

the 80s, as described in the introduction of (Davidson

et al., 1985). This implies that one of such three as-

pects (consistency, availability and network partition

tolerance) should be sacriﬁced in order to fully main-

tain the other two.

Database sharding and the support of different

isolation levels provide a good basis for guarantee-

ing network partition tolerance and availability while

still maintaining a workable degree of replica consis-

tency, as suggested in other recent papers (Gilbert and

Lynch, 2012; Bailis et al., 2013). In our case, this is

complemented with the management of different de-

grees of data freshness in each update-related layer.

Such approach provides sequential consistency (Lam-

port, 1979) when no network partition exists and it is

a good basis for achieving eventual consistency (Terry

et al., 1994) while any network partition arises and is

later recovered.

Another important principle for designing scal-

able databases is the usage of epidemic propagation of

updates (Holliday et al., 2003), in order to enhance the

basis provided by asynchronousreplication. It is well-

known that a scalable system should avoid all poten-

tial contention points. Asynchronous update propaga-

tion is a key factor in such elimination of contention.

It allows a fast answer to the client from the delegate

replica (i.e., the one that has directly served the trans-

action) while the updates are still being propagated to

the remaining replicas, or even before that propaga-

tion is initiated.

The ﬁrst papers proposing epidemic update prop-

agation, e.g. (Agrawal et al., 1997), were based on a

lazy causal broadcast mechanism and allowed multi-

ple forwarding steps that did not break such causal

order. This causal broadcast was implemented in-

cluding all causally-preceding writesets that were not

yet acknowledged as delivered by the remaining repli-

cas. Thus, that broadcast never blocked the receiving

nodes and easily allowed them to build up the infor-

mation needed for certifying concurrent transactions.

As providing a conﬁgurable degree of data fresh-

ness without compromising the correctness of the ap-

plications that use these data is not that straightfor-

ward, epidemic replication should be combined with

database partitioning.

Actually, lazy or epidemic database replication

has been used in recent papers (Daudjee and Salem,

2006; Terry, 2008; Arrieta-Salinas et al., 2012) to

obtain good scalability and performance even when

the system is geographically dispersed. However, in

these works there is very little discussion about the

procedure to obtain the best data epidemic replica-

tion policy and system conﬁguration that maximize

the database performance.

Chive:ASimulationToolforEpidemicDataReplicationProtocolsBenchmarking

429

Client

Application Logic

Client Library

Replication Protocol n

GCS

Replication Protocol 2

GCS

Replication Protocol 1

GCS

Client

Application Logic

Client Library

Metadata Manager

Workload Manager

Transaction Manager

Replication Manager

Metadata

Repository

Replication clusters

Data flow

Control flow

Client requests

Monitoring info

Figure 1: An abstraction of a cloud storage system with transactional support.

3 SYSTEM MODEL

The proposed approach is committed to accurately

simulate epidemic data replication protocols. This

section deﬁnes the system model used to build the

simulator, and discusses the obtained correctness cri-

terion of the simulated epidemic replication strate-

gies. We assume a dynamic distributed system that

stores a database (see Figure 1) where three differ-

ent roles may be distinguished as similarly done in

Google’s GFS or ElasTraS (Das et al., 2010): (1) a

set of client applications that interact with the system;

(2) a metadata manager (MM) that holds the system

state (which is stored in the metadata repository) and

orchestrates the communication between clients and

replicas; and, (3) a set of replication clusters (RCs),

each storing one data partition.

Clients have a library that permits their interac-

tion with the system. Firstly, they connect with the

MM to locate the partitions they want to access and,

afterwards, issue transactions directly with a dele-

gate of the given RC. Respectively, the MM stores:

the mapping between each data item and its associ-

ated partition; the set of available replicas; the map-

ping between a node and its RC with its respective

level/freshness; and, the statistics of each replica.

Focusing on the RC components, a different RC

exists for each partition. The replicas that form each

RC are organized in a hierarchical way. Each tier

is associated to a freshness degree where the higher

the freshness degree, the more recent the versions of

stored data items are. The core level of each hierar-

chy comprises a small set of replicas that propagate

updates among themselves by means of a traditional

replication protocol (Wiesmann and Schiper, 2005)

(as determined by the MM) that makes use of a group

communication service (GCS) (Chockler et al., 2001)

to handle the messages among replicas and monitor

the replicas belonging to the group. Also, the repli-

cas that do not belong to the core level are distributed

into several levels forming a tree whose root is the

aforementioned core level, where a replica of a given

level acts as a backup for a replica of its immediately

upper level and may also act as a primary for repli-

cas of its lower level. To exploit the advantages of

in-memory approaches (i.e., avoiding disk stalls and

using the thread-to-data policy), we assume that every

replica keeps all its data in main memory.

When a replica (r) receives a transaction (t) from

a client, it ﬁrst checks that the partition where the

client intends to execute it is the same as the one man-

aged by the RC that r belongs to. In case t is a read-

only transaction, the freshness related to the hierarchy

level to which r belongs must be capable of fulﬁlling

the freshness limit imposed by t. In case this state-

ment is satisﬁed, r executes t and sends the result to

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

430

the client. Read-only transactions are regularly exe-

cuted without delay, although their execution might

be delayed to meet different consistency constraints

and further elaborate the notion of freshness. For in-

stance, in case t demanded read-your-writes consis-

tency (Vogels, 2009), before executing t the replica

would have to apply all update transactions from that

client that happened before t. On the other hand, if t

is an update transaction, it can only be processed if r

belongs to the core level of the hierarchy and is not a

read-only replica. If afﬁrmative, t is delegated to the

replication protocol. Once t commits, each replica of

the core level will be able to asynchronously prop-

agate the changes (in the form of writesets, the set

of tuples that are created, modiﬁed or deleted by the

transaction) to its children through the point-to-point

connections following an epidemic propagation pro-

tocol which is the main topic of this paper.

As stated previously, this is a good approach for

managing transactions in a highly scalable environ-

ment (Gilbert and Lynch, 2012; Bailis et al., 2013;

Vogels, 2009). In general, we can achieve different

levels of consistency depending on the hierarchy level

where t accesses the data. We can guarantee that the

replication protocol running at the core of the cor-

responding partition (Wiesmann and Schiper, 2005)

ensures data consistency and provides one copy (1C)

schedules even in the presence of failures (Bernstein

et al., 1987; Fekete and Ramamritham, 2010). With-

out generalization loss, we assume t only accesses a

single partition; therefore, if t only accesses the core

nodes of a partition, it will behave as if it were ex-

ecuted in a traditional replicated database. Hence,

the consistency criterion fulﬁlled will correspond to

the consistency guarantees ensured by the replication

protocol that manages that core level, normally 1C-

Serializability (1CS) (Bernstein et al., 1987) or 1C-

Snapshot-Isolation (1SI) (Lin et al., 2009) depending

on the replication protocol. In case t accesses other

levels of the hierarchy apart from the core level, the

consistency criterion fulﬁlled will be 1SI, as update

transactions are serially executed at the replicas of the

core level whereas read-only transactions can be for-

warded to lower hierarchy levels assuming that they

might obtain a stale (but consistent) snapshot of the

database. However, a multi-partition transaction t

′

has no notion of consistency across data partitions,

but that data versions are obtained from a valid com-

mitted snapshot in each partition and we obtain one-

copy-multi-version (1MV) schedules.

Apart from this, update transactions executed at

the core replicas must eventually get propagated to

the rest of replicas inside their associated RC no mat-

ter how many replica failures and network partitions

occur, so as to ensure global correctness. Any replica

belonging to a hierarchy layer different than the core

layer of an RC receives its updates from a replica of

the upper layer via a propagation mechanism (ﬂood-

ing, epidemic, etc.) (Baldoni et al., 2006) which en-

sures that updates are received (and therefore exe-

cuted) in order; provided that all committed update

transactions have a unique version number which per-

mits them to be ordered at any node (this is the ver-

sion number assigned by the replication protocol on

each RC). This corresponds to the notion of eventual

consistency; i.e., there is some time point when if no

new updates arrive then all replicas will converge to

the same state.

For the sake of this paper, this model considers

different variations of propagating updates across the

hierarchy tree of an RC and check which one is the

best in terms of: number of messages exchanged, cov-

erage and load. Hence, we will start with a very sim-

ple propagation mechanism and present several varia-

tions of epidemic algorithms, more precisely the kind

of propagation, to see which one ﬁts best in our trans-

action model scenario.

• TTL-based: This method of propagation is the

simplest one: when a node receives an update, it

spreads it to all its neighbors but the sender of the

message. The update has a number attached; the

TTL (time-to-live). With each ”hop” the TTL is

reduced by one. When the TTL is zero the update

cannot be propagated anymore.

• Epidemic: It has recently gained popularity be-

cause it provides a scalable way of propagating

information in a system. It is based on a model

that emulates the propagation of an epidemic dis-

ease on a population. Its execution model is rather

simple but presents several variations. A node be-

comes “infected” with an update, and spreads it

to the neighbors. The original node may “die”

in the process, prohibiting it from spreading the

disease. This mechanism allows the “disease” to

stop spreading without the need of consensus and

makes it fast to propagate. Additionally, it does

not generate a lot of trafﬁc. The variations are the

following: push, a node selects one neighbor and

sends to it the updates; pull, a node selects one

neighbor, and retrieves its updates; and, push &

pull, a node selects one neighbor, and they inter-

change updates.

• Rollback: Both previous propagation models have

a small chance of not reaching all the nodes. This

does not happen in a traditional model of a tree

where nodes know the topology (unless there is

a failure). In our model, when a node receives

newer information and notices a gap between its

Chive:ASimulationToolforEpidemicDataReplicationProtocolsBenchmarking

431

information and the new update, such receiver

may ask the node that gave the information for

more.

To compare the different algorithms it is neces-

sary to use one or more metrics. In this case we have

selected three metrics which, in our opinion, are the

most determinant in developing a scalable database

with transactional guarantees.

• Trafﬁc: Measures the amount of messages sent

between nodes in a given round. A protocol that

sends too many messages ends up being expen-

sive in hardware cost so it is important to keep

this metric low. We need to see the average trafﬁc

between rounds and the standard deviation (which

tells us if the trafﬁc is stable or has strong peaks).

• Coverage per round: Indicates how fast an update

transaction reaches all the nodes of its associated

RC. Hence, we will normalize coverage using the

partitions and set its threshold to the ﬁrst round

in which a given coverage percentage appears. To

this end we will analyze how fast (in simulation

rounds) transaction propagations reach 50% and

90% coverage.

• Load per node: Number of messages that reach

a node. Although related with the trafﬁc, it pro-

vides different information. For example, a con-

sistent low load per node, even in a high trafﬁc

scenario, signals a stable distribution. In contrast,

a low average trafﬁc distribution with a high load

in a group of nodes means instability and will be

an important issue to be ﬁxed. We will evaluate

load in write and read nodes.

4 SOFTWARE

All experiments were performed using a discrete

event simulator (see Figure 2) coined as Chive. The

simulator is written in Java using JUNG (JUNG,

2014) to support graph operations and visualization,

plus JChart2D (JChart2D, 2014) to plot the different

graphs. We have developed a software that simulates

this system model through time, adding a dynamic vi-

sualization of the state of the network. We mainly fo-

cused on the layered structure of nodes inside an RC

to evaluate different epidemic propagation protocols

according to the aforementioned metrics using differ-

ent scenarios. Up to our knowledge, there have been

also attempts to develop epidemic simulation models

like in (Baldoni et al., 2006; Bakhshi, 2011). The ﬁrst

one (Baldoni et al., 2006) uses its own replication pro-

tocol to maintain eventual consistency based on epi-

demic models and uses a random graph but lacks of

transactional support. Whereas the latter (Bakhshi,

2011) uses probabilistic models and does not consider

transactions. This approach can be useful when the

model behavior is known in advance; e.g., consider a

full graph with no partitions or tiers.

Figure 2: A screenshot of Chive.

We need to deﬁne a model that can simulate the

reality of our distributed database model while ab-

stracting the remaining features that are not of interest

in our discussion (like RAM usage, number of disk

writes). We are going to use an undirected graph,

where each vertex represents a node. A node is a pro-

cess or machine that holds a partition of the database

that belong to a given RC. Each of these nodes has to

apply a sequence of update transactions coming from

the core layer (or tier) of each RC and forward these

updates to the rest of nodes.

To simulate the timelines ﬂow we are going to use

a cycle system, which allows us to control the events

(like failures or new updates) and simplify the un-

derlying network stack. A cycle is an arbitrary time

amount where a node can send and receive messages.

Recall that each committed update transaction has a

unique version so each node can infer the order of the

updates to be applied with no coordination with other

nodes.

Bearing all these features in mind, we have to gen-

erate the initial graph. Each edge in the graph repre-

sents a communication link between two nodes. We

are going to consider several approaches:

• Complete: This is the simplest scenario where all

nodes are connected to each other. The updates

can come from anywhere, but the system needs

to synchronize the amount of messages received.

Hence, we do not distinguish among core layer

and outer layers, as well as dividing into partitions

since it does not statistically make any difference.

• Random: Using the Barab´asi-Albert (Barab´asi

and Albert, 1999) method. Such method is able

to adequately manage growth (i.e., the fact that

the number of nodes in the network increases

over time) and is based on preferential attach-

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

432

ment. Preferential attachment means that nodes

with higher degree have stronger ability to obtain

new links when these are added to the network.

Under this graph we assume a two tier graph. The

ﬁrst one corresponds to the core layer whilst the

remainder constitute satellites. Connections be-

tween the two layers are randomly generated, al-

though this approach is valid in terms of the met-

rics considered here.

• Proposed x/y: Partition-tiered graph with x parti-

tions and y tiers.

5 RESULTS

To demonstrate the versatility of the proposed simu-

lator, in this section we present the results of different

simulation runs of the aforesaid epidemic replication

strategies over 1000 rounds. If we assume one round

is one second (like Cassandra(Apache Software Foun-

dation, 2014)), this simulation will last 16.6 minutes.

We have considered three different metrics to mea-

sure: trafﬁc; coverage; and, load. Each one is run

under two different workload scenarios (update inten-

sive and read intensive) which will derive two new

tables, read and update intensive, respectively. The

update intensive is modeled with a probability p of ar-

riving a new update transaction in each round. Thus,

we have p = 0.2 for read-intensive scenarios; and,

p = 0.9 for update-intensive scenarios.

Each table contains the following information.

The ﬁrst column indicates the algorithm used for

graph generation: Complete, Random and Proposed

x/y). The second column states the type of propaga-

tion protocol with these parameters:

• Simple, k: it is a simple spread protocol with a

TTL of k. Each node will receive an update trans-

action and spread it to all its neighbors with a TTL

decremented in one unit.

• Epidemic, type, feedback, count or coin, k: It is

an epidemic protocol. The type may be push, pull

and push&pull. The latter is represented as p&p

in the table. If it uses feedback (represented as

’fbk’) the node responds with its state when it re-

ceives an already applied update transaction. Oth-

erwise, a ’nof’ (for “no feedback”) is used in that

second parameter. The coin and count parameters

determine if the propagation ﬁnishes (dies) with a

probability 1/k or after k spreads, respectively.

The last two columns are the actual measure-

ments, the average and standard deviation, whose

magnitude depends on the metric. In the case of traf-

ﬁc and load, they represent the number of messages

whereas the coverage is measured in terms of rounds.

5.1 Trafﬁc

In Tables 1 and 2, we present the average trafﬁc in the

system in each round and its standard deviation.

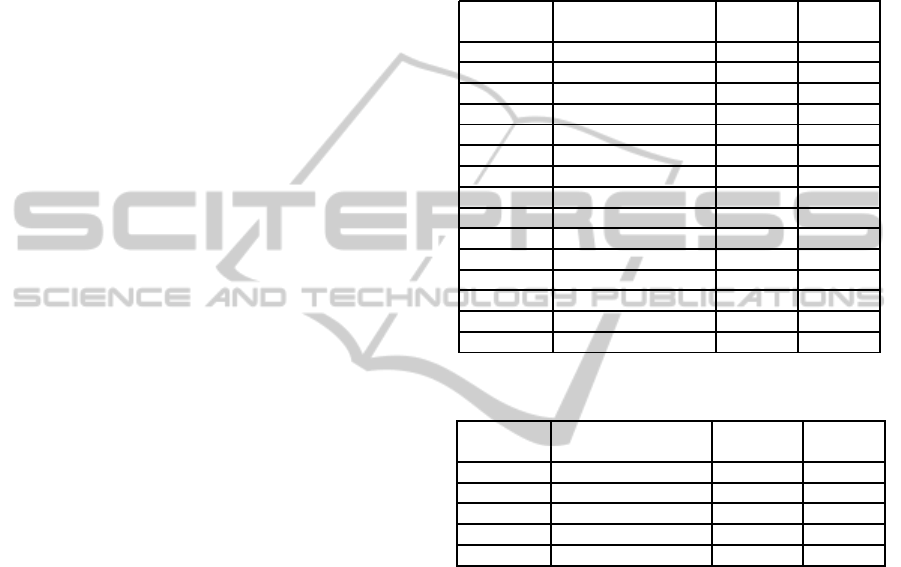
Table 1: Trafﬁc - Read Intensive Workload.

GRAPH PROPAGATION MEAN STD.

TYPE PROTOCOL DEV.

Complete simple, k=3 446.082 927.310

Random simple, k=3 65.742 99.819

Complete push,fbk,count,k=3 78.873 55.468

Complete pull,fbk,count,k=3 119.985 58.229

Complete p&p,fbk,count,k=3 124.277 75.958

Complete p&p,fbk,coin,k=3 142.462 83.949

Complete p&p,nof,coin,k=3 81.324 28.583

Random p&p,fbk,count,k=3 126.644 78.330

Prop.4/3 push,fbk,count,k=3 58.103 38.476

Prop.4/3 pull,fbk,count,k=3 113.313 40.288

Prop.4/3 p&p,fbk,count,k=3 108.247 52.138

Prop.4/3 p&p,fbk,count,k=5 108.291 52.790

Prop.4/3 p&p,nof,count,k=3 64.204 14.596

Prop.4/5 p&p,fbk,count,k=3 105.017 46.264

Prop.5/3 p&p,fbk,count,k=3 57.464 35.268

Table 2: Trafﬁc - Update Intensive Workload.

GRAPH PROPAGATION MEAN STD.

TYPE PROTOCOL DEV.

Complete simple, k=3 2181.441 751.772

Random simple, k=3 241.171 93.061

Complete p&p,fbk,count,k=3 433.721 87.494

Random p&p,fbk,count,k=3 409.395 99.107

Prop.4/3 p&p,fbk,count,k=3 357.160 72.299

These results show that a simple (i.e., TTL-based)

propagation strategy needing a fully connected net-

work is unable to scale. The average amount of prop-

agated messages is too high and its standard deviation

also shows that the system is unable to absorb and

process such amount of messages. However, when

read intensive loads are considered (Table 1) a TTL-

based propagationstrategy combined with a randomly

generated propagation graph following the Barab´asi-

Albert method needs an acceptable amount of propa-

gated messages. Unfortunately, its standard deviation

is still high. This random topology does not main-

tain these good results when it is combined with a

push-and-pullpropagation,since it almost doubles the

amount of propagated messages.

The best strategy in a load with a low percent-

age of update transactions consists in using our pro-

posed topology with 5 partitions and 3 tiers, combined

with a propagation based on a push-and-pull strategy

with feedback and three forwarding steps. It achieves

Chive:ASimulationToolforEpidemicDataReplicationProtocolsBenchmarking

433

a minimal mean (57.5 msgs/round) and quite a low

standard deviation (35.27).

With write intensive loads (see Table 2) a TTL-

based propagation strategy (with 3 forwarding steps)

combined with a randomly generated topology pro-

vides a minimal mean amount of propagated mes-

sages with a moderate standard deviation.

5.2 Coverage

Tables 3 and 4 contain information about how many

rounds the algorithm needs on average to reach a cer-

tain coverage threshold. Such threshold is given as

the percentage of nodes that have received the new

values being propagated, in our case 50% and 90% of

the total nodes.

Table 3: Coverage - Read Intensive Workload.

GRAPH PROPAGATION ROUNDS

TYPE PROTOCOL 50% 90%

Complete simple, k=3 1 1

Random simple, k=3 2 3

Complete push,fbk,count,k=3 5 8

Complete pull,fbk,count,k=3 6 8

Complete p&p,fbk,count,k=3 4 5

Complete p&p,fbk,coin,k=3 4 5

Complete p&p,nof,coin,k=3, 4 7

Random p&p,fbk,count,k=3 3 5

Proposed 4/3 push,fbk,count,k=3 5 8

Proposed 4/3 pull,fbk,count,k=3 6 11

Proposed 4/3 p&p,fbk,count,k=3 3 5

Proposed 4/3 p&p,fbk,count,k=5 3 5

Proposed 4/3 p&p,nof,count,k=3 4 8

Proposed 4/5 p&p,fbk,count,k=3 3 5

Proposed 5/3 p&p,fbk,count,k=3 5 11

Table 3 shows that the TTL-based propagation

strategy with a randomly (Berab´asi-Albert) generated

topology is, among the best combinations obtained

in the trafﬁc analysis of the previous section, the one

needing a minimal number of rounds to reach an ac-

ceptable coverage. It only needs 2 rounds to reach

50% of the nodes and 3 rounds to reach 90% of the

nodes. In order to reach these minimal values we

are assuming that the node that initially served each

update transaction was that with the maximal degree

(i.e., with the maximum number of connected neigh-

bor nodes). If an application chooses another node as

its delegate replica the number of propagation rounds

will be slightly higher.

Our best proposed conﬁguration considering traf-

ﬁc (5 partitions with 3 tiers, push-and-pull propaga-

tion with feedback and 3-round forwarding) needs a

high amount of communication rounds to achieve this

analyzed coverage (5 and 11 rounds, respectively).

This is not a serious drawback since our replication

strategy still provides a consistent view of the updated

nodes, even they do not maintain the latest version.

Table 4: Coverage - Update Intensive Workload.

GRAPH PROPAGATION ROUNDS

TYPE PROTOCOL 50% 90%

Full simple, k=3 1 1

Random simple, k=3 2 3

Full p&p,fbk,count,k=3 4 5

Random p&p,fbk,count,k=3 3 5

Proposed 4/3 p&p,fbk,count,k=3 3 5

The usage of write intensive loads (as shown in

Table 4) does not introduce any modiﬁcation to the

values presented in Table 3 since the coverage does

not depend on the workload being considered but only

on the topology and propagation strategy.

5.3 Load

Tables 5 and 6 contain the number of messages re-

ceived by certain nodes in each turn. We check the

average of nodes that are in the core tier and nodes

that are in the read tiers.

Table 5: Load in the Nodes - Read Intensive Workload.

GRAPH PROPAGATION WRITE LOAD READ LOAD

TYPE PROTOCOL MEAN DEV. MEAN DEV.

Complete simple, k=3 18.546 8.918 18.546 8.918

Random simple, k=3 1.191 1.815 1.191 1.815

Complete push,fbk,count,k=3 1.573 1.109 1.573 1.109

Complete pull,fbk,count,k=3 1.799 0.675 1.799 0.675

Complete p&p,fbk,count,k=3 2.097 1.137 2.097 1.137

Complete p&p,fbk,coin,k=3 2.355 1.256 2.355 1.256

Complete p&p,nof,coin,k=3 1.622 0.571 1.622 0.571

Random p&p,fbk,count,k=3 2.015 1.105 2.015 1.105

Prop.4/3 push,fbk,count,k=3 1.006 0.728 1.257 0.882

Prop.4/3 pull,fbk,count,k=3 1.337 0.786 1.813 0.610

Prop.4/3 p&p,fbk,count,k=3 1.762 1.086 1.981 0.888

Prop.4/3 p&p,fbk,count,k=5 1.682 1.062 1.956 0.915

Prop.4/3 p&p,nof,count,k=3 1.021 0.620 1.344 0.481

Prop.4/5 p&p,fbk,count,k=3 1.524 0.792 1.933 0.819

Prop.5/3 p&p,fbk,count,k=3 0.788 0.607 1.147 0.827

As already shown in the trafﬁc analysis, a com-

plete graph with a TTL-based propagation is unable

to scale. This fact is also clearly shown here, in both

tables. Thus, with a read intensive load each node

manages around 19 messages per round (with a stan-

dard deviation of 9), while this value grows up to 44

with a write intensive load.

With a read intensive load, a randomly generated

graph with TTL-based propagation provides excel-

lent values for both reading and writing operations on

nodes with a low standard deviation (1.8). However,

the best values are provided by our 5/3 topology pro-

posal (i.e., using 5 partitions and 3 tiers) that only re-

quires on average 0.8 messages on updated nodes and

1.1 messages on read nodes with a standard deviation

lower than in the random topology.

Considering write intensive loads, the random

topology with TTL-based propagation provides the

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

434

Table 6: Load in the Nodes - Update Intensive Workload.

GRAPH PROPAGATION WRITE LOAD READ LOAD

TYPE PROTOCOL MEAN DEV. MEAN DEV.

Full simple, k=3 43.611 15.036 43.611 15.036

Random simple, k=3 4.620 1.790 4.620 1.790

Full p&p,fbk,count,k=3 6.930 1.385 6.930 1.385

Random p&p,fbk,count,k=3 6.545 1.510 6.545 1.510

Prop.4/3 p&p,fbk,count,k=3 5.678 1.710 5.993 1.472

minimal average workload per node. However, ran-

dom topologies with a push-and-pull propagation

strategy still introduce a higher workload than our

best 4/3 topology proposal. As a result, this shows

that our proposed strategy is a good approach for scal-

able data replication with easily selectable degrees of

freshness.

6 CONCLUSIONS

This paper presents Chive, a simulation tool aimed

at guiding the design process of replicated systems

based on epidemic protocols. Chive takes into ac-

count a set of metrics that allow to compare the per-

formance and scalability capabilities of a variety of

replication protocols and system settings under dif-

ferent workload scenarios.

Performed experiments show that complete

graphs with a simple spreading protocol suffer from a

serious scalability limitation in update intensive sce-

narios due to the elevated number of messages in-

volved. Using a Barab´asi-Albert graph alleviates this

problem, as it reduces trafﬁc while maintaining fast

updates, although it still requires a write consensus.

In contrast, our proposed conﬁguration has shown to

be the most stable. In particular, push&pull is the

most effective method, although it generates more

trafﬁc than the push strategy. Removing feedback

also reduces trafﬁc signiﬁcantly, although it requires

more time to reach an acceptable coverage thresh-

old. Furthermore, it is necessary to establish a proper

trade-off between the number of nodes and the num-

ber of tiers, since increasing the number of tiers re-

duces both overall trafﬁc and individual load (since

trafﬁc spreads more evenly among nodes and there is

less need for rollbacks), at the expense of degrading

the coverage metric.

Chive provides a solid foundation for future ex-

tensions that will allow to model the features of a dis-

tributed system more accurately. For example, Chive

could take into account other external factors such as

the read load coming from clients and their freshness

requirements. Moreover,other variables regarding the

behavior of system nodes could be incorporated, such

as the maximum capacity of each node or the prob-

ability of a node failure. Apart from this, providing

Chive with the ability to dynamically tune the simula-

tion settings to different workload patterns (by adding

or removing system nodes or changing the graph con-

ﬁguration) and modeling the data transfer operations

involved when a node joins the system would provide

a sound basis for adapting replicated systems to un-

predictable workload scenarios, by determining the

optimal conﬁguration depending on the current work-

load characteristics.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish Gov-

ernment under research grant TIN 2012-37719-C03.

REFERENCES

Agrawal, D., El Abbadi, A., and Steinke, R. C. (1997). Epi-

demic algorithms in replicated databases (extended

abstract). In 16th ACM Symp. on Principles of

Database Syst. (PODS), pages 161–172, Tucson, Ari-

zona, USA. ACM Press.

Apache Software Foundation (2014). Apache

Cassandra Gossiper documentation.

http://wiki.apache.org/cassandra/ArchitectureGossip/.

Arrieta-Salinas, I., Armend´ariz-I˜nigo, J. E., and Navarro, J.

(2012). Classic replication techniques on the cloud.

In Seventh International Conference on Availability,

Reliability and Security, Prague, ARES 2012, Czech

Republic, August 20-24, 2012, pages 268–273.

Bailis, P., Davidson, A., Fekete, A., Ghodsi, A., Hellerstein,

J. M., and Stoica, I. (2013). Highly available transac-

tions: Virtues and limitations. PVLDB, 7(3):181–192.

Bakhshi, R. (2011). Gossiping Models: Formal Analysis

of Epidemic Protocols. PhD thesis, Vrije Universiteit,

Amsterdam.

Baldoni, R., Guerraoui, R., Levy, R. R., Qu´ema, V., and

Piergiovanni, S. T. (2006). Unconscious eventual con-

sistency with gossips. In Proceedings of the 8th Inter-

national Conference on Stabilization, Safety, and Se-

curity of Distributed Systems, SSS’06, pages 65–81,

Berlin, Heidelberg. Springer-Verlag.

Barab´asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. Science, 286(5439):509–

512.

Bernstein, P. A., Hadzilacos, V., and Goodman, N. (1987).

Concurrency Control and Recovery in Database Sys-

tems. Addison-Wesley.

Chockler, G., Keidar, I., and Vitenberg, R. (2001).

Group communication speciﬁcations: a comprehen-

sive study. ACM Computing Surveys, 33(4):427–469.

Das, S., Agarwal, S., Agrawal, D., and Abbadi, A. E.

(2010). ElasTraS: An elastic, scalable, and self man-

aging transactional database for the cloud. Technical

report, CS, UCSB.

Daudjee, K. and Salem, K. (2006). Lazy database repli-

cation with snapshot isolation. In 32nd Intnl. Conf.

Chive:ASimulationToolforEpidemicDataReplicationProtocolsBenchmarking

435

on Very Large Data Bases (VLDB), pages 715–726,

Seoul, Korea. ACM Press.

Davidson, S. B., Garcia-Molina, H., and Skeen, D. (1985).

Consistency in partitioned networks. ACM Comput.

Surv., 17(3):341–370.

Eugster, P. T., Guerraoui, R., m. Kermarrec, A., and Mas-

souli, L. (2004). From epidemics to distributed com-

puting. IEEE Computer, 37:60–67.

Fekete, A. D. and Ramamritham, K. (2010). Consistency

models for replicated data. In Replication, pages 1–

17.

Gilbert, S. and Lynch, N. A. (2002). Brewer’s conjecture

and the feasibility of consistent, available, partition-

tolerant web services. SIGACT News, 33(2):51–59.

Gilbert, S. and Lynch, N. A. (2012). Perspectives on the

CAP theorem. IEEE Computer, 45(2):30–36.

Holliday, J., Steinke, R. C., Agrawal, D., and El Abbadi, A.

(2003). Epidemic algorithms for replicated databases.

IEEE Trans. Knowl. Data Eng., 15(5):1218–1238.

JChart2D (2014). JChart2D, precise visualization of data.

http://jchart2d.sourceforge.net/.

Johnson, R., Pandis, I., and Ailamaki, A. (2014). Eliminat-

ing unscalable communication in transaction process-

ing. The VLDB Journal, 23:1–23.

JUNG (2014). JUNG - Java Universal Network/Graph

Framework. http://jung.sourceforge.net/.

Lamport, L. (1979). How to make a multiprocessor com-

puter that correctly executes multiprocess programs.

IEEE Trans. Computers, 28(9):690–691.

Lin, Y., Kemme, B., Jim´enez-Peris, R., Pati˜no-Mart´ınez,

M., and Armend´ariz-I˜nigo, J. E. (2009). Snapshot iso-

lation and integrity constraints in replicated databases.

ACM Trans. Database Syst., 34(2).

Navarro, J., Armend´ariz-I˜nigo, J. E., and Climent, A.

(2011). An adaptive and scalable replication protocol

on power smart grids. Scalable Computing: Practice

and Experience, 12(3).

Sancho-Asensio, A., Navarro, J., Arrieta-Salinas, I., Ar-

mend´ariz-I˜nigo, J. E., Jim´enez-Ruano, V., Zabal-

los, A., and Golobardes, E. (2014). Improving

data partition schemes in smart grids via cluster-

ing data streams. Expert Systems with Applications,

41(13):5832 – 5842.

Shoens, K. A. (1986). Data sharing vs. partitioning for ca-

pacity and availability. IEEE Database Eng. Bull.,

9(1):10–16.

Stonebraker, M. (1986). The case for shared nothing. IEEE

Database Eng. Bull., 9(1):4–9.

Stonebraker, M. (2010). SQL databases v. NoSQL

databases. Communications of the ACM, 53(4):10–11.

Terry, D. B. (2008). Replicated data management for mobile

computing. Synthesis Lectures on Mobile and Perva-

sive Computing, 3(1):1–94.

Terry, D. B., Demers, A. J., Petersen, K., Spreitzer, M.,

Theimer, M., and Welch, B. B. (1994). Session guar-

antees for weakly consistent replicated data. In 13th

Intnl. Conf. Paral. Dist. Inform. Syst. (PDIS), pages

140–149, Austin, Texas, USA. IEEE-CS Press.

Vogels, W. (2009). Eventually consistent. Commun. ACM,

52(1):40–44.

Wiesmann, M. and Schiper, A. (2005). Comparison of

database replication techniques based on total order

broadcast. IEEE TKDE, 17(4):551–566.

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

436