
An LTL Semantics of Business Workflows with Recovery
Luca Ferrucci
1,2
, Marcello M. Bersani
2
and Manuel Mazzara
3
1
ISTI-CNR, Pisa, Italy
2
Dipartimento di Elettronica Informazione e Bioingegneria, Politecnico di Milano, Milan, Italy
3
Innopolis University, Russia and ETH Zürich, Zürich, Switzerland
Keywords:
Business Workflow, Recovery Framework, Formal Methods, Temporal Logic, Semantics.
Abstract:
We describe a business workflow case study with abnormal behavior management (i.e. recovery) and demon-
strate how temporal logics and model checking can provide a methodology to iteratively revise the design
and obtain a correct-by construction system. To do so we define a formal semantics by giving a compilation
of generic workflow patterns into LTL and we use the bound model checker Zot to prove specific properties
and requirements validity. The working assumption is that such a lightweight approach would easily fit into
processes that are already in place without the need for a radical change of procedures, tools and people’s
attitudes. The complexity of formalisms and invasiveness of methods have been demonstrated to be one of the
major drawback and obstacle for deployment of formal engineering techniques into mundane projects.
1 INTRODUCTION
Nowadays Internet access is widespread and people
use the internet for a wide range of activities, among
others to purchase goods and services. In Europe in
2012, 75% of individuals aged 16 to 74 had used the
internet in the previous 12 months, and nearly 60% of
these reported that they had shopped online (data col-
lected by http://epp.eurostat.ec.europa.eu/). Presently
Internet purchases represents the most important way
of doing E-business while older systems are either
been canceled or improved in such a way that they
are able to run over the Internet infrastructure.
Together with the emerging of E-business and the
exigency of exchanging business messages between
trading partners, the concept of business integration
arose. Business integration is becoming necessary to
allow partners to communicate and exchange docu-
ments as catalogs, orders, reports and invoices, over-
coming architectural, applicative, and semantic dif-
ferences, according to the business processes imple-
mented by each enterprise. In order to be effective,
a business integration solution must also deal with
(non-functional) requirements such as dependability,
security, availability and compatibility.
In this work, our focus will be limited to the
dependability aspect of business integration and the
analysis of recovery solutions. In particular, we will
give a formal semantics to business workflows en-
riched with abnormal behaviour and recovery and will
address a methodology to define and verify specific
causal properties defined by designers. Causal prop-
erties allows to specify order relationships between
events and activities.
On Methods and Tools
Logics and model-checking have been successfully
used in the last decades for modelling and verifica-
tion of various types of hardware and software sys-
tems and have a stronger credibility in the scientific
community when compared with other formalisms.
We here give an LTL-based semantics of workflow
execution and use Zot (Pradella et al., 2008) model
checker for requirement verification. By applying
model-checking on the case study presented in this
paper, we demonstrate the feasibility of the verifica-
tion approach and how temporal logics can work for
both modelling and verification of (simple but real-
istic) business workflows inclusive of exception han-
dling. This work has to be intended as complementary
to what has been done in (Lucchi and Mazzara, 2007)
where a similar problem was approached in term of
Process Algebra. A comparison of approaches is left
as future work.
Differently from several others formalizations
only offering languages without methods – for a de-
tailed discussion see (Mazzara, 2009) and (Mazzara,
29
Ferrucci L., Bersani M. and Mazzara M..
An LTL Semantics of BusinessWorkflows with Recovery.
DOI: 10.5220/0005110000290040
In Proceedings of the 9th International Conference on Software Paradigm Trends (ICSOFT-PT-2014), pages 29-40
ISBN: 978-989-758-037-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2011) – our approach, together with software tools,
aims at offering a complete practical toolkit for soft-
ware and systems engineers working in the field of
workflow design. Following the line of (Gmehlich
et al., 2013) this approach goes under the correct-by-
construction paradigm and the idea of developing de-
pendable systems by integrating specific approaches
well-suited to each development phase.
The ideal process of workflow verification is an it-
erative process. In this work, we aim at providing an
instrument to designers for workflow revision, i.e. a
procedure to follow until the requirements are finally
met. To do this, we encode the workflow into a formal
language and, at the same time, we formally describe
specific requirements on the system. This is discussed
in Section 3. At this point, as shown in Section 4, cor-
rectness can be automatically determined via the Zot
model checker. As an outcome of model checking we
may need to revise the workflow in order to meet the
requirements.
A Descriptive Semantics
The role of temporal logics in verification and valida-
tion is two-fold. First, temporal logic allows abstract,
concise and convenient expression of required prop-
erties of a system. In fact, Linear Temporal Logic
(LTL) is often used with this goal in the verification of
finite-state models, e.g., in model checking (Baier and
Katoen, 2008). Second, temporal logic can be used
as a descriptive approach for specifying and mod-
elling systems (see, e.g., (Morzenti and San Pietro,
1994; Ferrucci et al., 2012)). A descriptive model is
based on axioms, written in some (temporal) logic,
which define the system through its general proper-
ties, rather than by an operational model based on
some kind of machine behaving in the desired way.
In this case, verification typically consists of satisfia-
bility checking of the conjunction of the model and of
(the negation of) its desired properties. For example,
in Bounded Satisfiability Checking (BSC) (Pradella
et al., 2013), Metric Temporal Logic (MTL) spec-
ifications on discrete time and properties are trans-
lated into propositional logic, in an approach simi-
lar to Bounded Model Checking of LTL properties of
finite-state machines.
Specifying temporal relations among events that
do not inherently behave in an operational way may
become rather hard when operational models are em-
ployed. This is the case for the system recovery
considered here. Exception handling is an event-
based paradigm that implements the asynchronous
exchange of warning events among actors that are part
of the system. The typical implementation of excep-
tion handling mechanisms – through logical rules of
the form if (cond) then throw(e) and try-catch blocks
– requires ad-hoc extensions of operational-based
formalisms by means of the definition of message-
passing primitives. Specifying exception handling
mechanisms through temporal logic does not require
extending LTL and also allows modelling of two sorts
of exceptions (punctual and non-punctual, see Sec-
tion 3) in a coherent and uniform way by providing
events that represent exceptions a suitable semantics.
Other Approaches and Novelty
Several approaches have been adopted in recent years
to provide formal semantics of business processes.
Most of them are very much bound to a specific
formalism accordingly extended to better cope with
modelling issues. These attempts mostly belong (but
not limited) to the process algebras, Petri nets or
model-based philosophies, with some raid into tem-
poral logics et similia too.
Mobile process algebra have been successfully
used in (Lucchi and Mazzara, 2007) that this work
intend to complement. Limitations of process alge-
bras approaches like the previous ones and, for ex-
ample, (Vaz and Ferreira, 2012) are related to the
fact that process algebras are based on equational
reasoning. From a practical perspective, this makes
verification tricky, difficult and certainly not user-
friendly, because verification is mainly carried out
by specific proof techniques that are used to prove
behavioural equivalence among processes. Further-
more, all these approaches mostly focus on the ver-
ification of reachability-based properties (with some
exceptions like (Calzolai et al., 2008)) and tool sup-
port is very limited (see (Mazzara and Bhattacharyya,
2010)). On the other side, other works like (Montesi
et al., 2014) provide a methodology and tool support
for the modelling phase, but do not cope with the ver-
ification phase and either do not belong to the correct-
by-construction paradigm.
Petri Nets supporters and van der Aalst ap-
proaches like Workflow Petri Nets (WPN) (Aalst,
1997) reached the objective of verification and tool
support to a much larger extent than other communi-
ties. This approach is based on extensions of previ-
ously existing formalisms and still represents an op-
erational model, which also inherits the relative over-
head. A successful attempt to overcome this issue
has been provided by (Yamaguchi et al., 2009) where
acyclic WPN are translated into a finite-state automa-
ton and verified against a suitable LTL property in or-
der to verify soundness.
Model-based approaches have also been used,
though to a much lesser extent and often in combi-
nation with testing, for validation of business crit-
ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends
30

ical systems. The B-model is one of the most
popular together with its reactive-systems extension
Event-B (Augusto et al., 2003). B and Event-B
are not lightweight methods. They do come with a
refinement-based methodology, but cannot easily be
embedded into already existing industrial processes
(Gmehlich et al., 2013).
In the domain of temporal logics, CTL has been
used to specify and enforce intertask dependencies
(Attie and Singh, 1993), and LTL for UML activ-
ity graphs verification (Eshuis and Wieringa, 2002).
Other temporal logics have also been used for simi-
lar objectives. In paricular, in (Baresi et al., 2012) a
complete and coherent semantics based on the TRIO
logic (Ghezzi et al., 1990) has been proposed for a
more consistent set of UML diagrams.
Recovery frameworks have been more rarely for-
malized in similar manners instead. This has to be
intended as another major contribution of the pa-
per. One of the first works formally discussing busi-
ness recovery in terms of long-running transactions is
(Butler and Ferreira, 2004). In (Dragoni and Maz-
zara, 2009) a simplified and clarified semantics of
WS-BPEL recovery framework has been presented in
terms of Process Algebras. In (Eisentraut and Spieler,
2009) the state-of-the-art in formalizing fault, com-
pensation and termination mechanisms of WS-BPEL
2.0 has been deeply investigated. More recently, an-
other model has been formulated for the description
of composite web services orchestrated by WS-BPEL
and with resources associated. The key contribution
of (Díaz et al., 2012) is the integration of WS-BPEL
with WSRF (Foster et al., 2004), a resource manage-
ment language, taking into account the main struc-
tural elements of WS-BPEL with event handling and
fault handling.
The working assumption is that a lightweight so-
lution would easily fit into processes that are already
in place without the need for a radical change of pro-
cedures, tools and people’s attitudes, which is actu-
ally the case for most of the aforementioned tech-
niques. The complexity of formalisms and invasive-
ness of methods have been demonstrated to be one of
the major drawback and obstacle for deployment of
formal engineering techniques into mundane projects
(Gmehlich et al., 2013), (Romanovsky and Thomas,
2013).
The rest of the paper is organized as follows: Sec-
tion 2 describes the case study of a workflow for order
processing. The semantics of workflows and excep-
tion handling is given using temporal logic in Section
3 where a general encoding into LTL is provided. In
Section 4 the implementation of this translation is il-
lustrated and tests have been carried out to validate
its correctness. Finally, Section 5 draws conclusive
remarks and focus on future developments.
2 WORKFLOWS WITH
RECOVERY
A business process is a set of logically related tasks
performed to achieve a well defined business out-
come. Examples of typical business processes are
elaborating a credit claim, hiring a new employee,
ordering goods from a supplier, creating a marketing
plan, processing and paying an insurance claim, and
so on. Many computer systems are already available
in the commercial marketplace to address the various
aspects of Business Process Management (BPM) and
automation.
An automated business process is generally called
business workflow, i.e a choreographed and system-
driven sequence of activities directed towards per-
forming a certain business task to completion. By
activity we mean an element that performs a specific
function within a process. Activities can be as sim-
ple as sending or receiving a message, or as complex
as coordinating the execution of other processes and
activities. A business process may encompass com-
plex activities some of which run on back-end sys-
tems such as, for example, a credit check, automated
billing, a purchase order, stock updates and shipping,
or even such frivolous activities as sending a docu-
ment and filling a form.
Workflow is commonly used to define the dy-
namic behaviour of business systems and originates
from business and management as a way of modelling
business processes that could wholly or partially be
automated. It has evolved from the notion of process
in manufacturing and offices because these processes
are the result of trying to increase efficiency in routine
work activities since industrialization.
The view on a workflow which is inherited from
the BPM perspective – i.e. the way in which workflow
designers may see a system – is somehow different
from the way formalists see it. Therefore, to fill the
gap between the formal and informal world, we will
provide the reader with a precise understanding in-
troducing a formal definition of a business workflow.
However, our notation is suitably abstract enough to
represent a large number of different modelization
formalisms, such as those based on State Machines
(Statecharts (Harel, 1987), UML Activity Diagrams
(OMG, 2005) and Petri Nets) or specialized to rep-
resent business processes, such as BPEL (OASIS,
2007). In fact, one of the purposes of this work is
defining a general notation able to include most of the
AnLTLSemanticsofBusinessWorkflowswithRecovery
31

specialized constructs of these languages, by abstrac-
tion. How this abstraction is performed is out of the
scope of the paper.
A workflow is a directed graph which is defined
by pair (A, T ), where A is a finite non empty set of
places (or activities) and T is a relation that is defined
as T ⊆ A × A. Elements of T are pairs (p, q), with
p, q ∈ A, that are called transitions (later indicated by
t
pq
). Let a be a place of A. Set out(a) is the set of
outgoing transitions starting from a which is defined
as {(a, q) | q ∈ A, (a, q) ∈ T }. Set in(a) is the set of
ingoing transitions leading to p which is defined as
{(q, a) | q ∈ A, (q, p) ∈ T }.
We assume that |out(a)| ≥ 1, for all a ∈ A, except
for place end, and that |in(a)| ≥ 1, for all a ∈ A, ex-
cept for place start.
A finite path from a to a
0
is a (finite) sequence of
pairs (a
0
, a
1
). . . (a
n−1
, a
n
) with a
0
= a and a
n
= a
0
,
such that (a
i
, a
i−1
) ∈ T , for all 1 ≤ i ≤ n. An in-
finite path from a is an (infinite) sequence of pairs
(a
i
, a
i−1
) ∈ E, for all i ≥ 1, where a
0
= a. Throughout
the paper, we assume that workflows are structurally
correct, that is, such that there exists at least one path
from place start to (any) place end. Informally, an ex-
ecution of a workflow is the superposition of paths of
the workflow starting from the initial place. The LTL
modelling allows us to define precisely all the execu-
tions of a workflow.
Each activity of a workflow may have a specific
semantics that forces the execution to be compliant
with some specific rules. In general, endowing activi-
ties with a semantics is not achievable only by con-
sidering workflows as graphs and the definition of
complex behaviours may require more specific and
expressive formalisms. This is the case of condi-
tional cases and split-join activities that we consider
in this paper whose semantics can be easily obtained
by defining concise LTL formulae. Conditional cases
model if-then-else blocks provided with the usual se-
mantics. If the condition holds the “then” branch
is executed otherwise the execution flow follows the
“else” branch. In this paper, we do not model guards
explicitly, though conditional expressions over finite
domains can be easily introduced, as the effort of the
work is focused on the exception recovery mecha-
nism. Split-join activities model the parallel execu-
tion of two (or more) branches of the workflow that
starts concurrently when activity split is executed and
eventually synchronize their computations in corre-
spondence with the associated join activity. We as-
sume that conditional cases and split-join are fictitious
activities with non relevant time duration.
We consider workflows that are endowed with ex-
ceptions, i.e., specific events (or signals) representing
erroneous configurations that occur during the execu-
tion and that may prevent the workflow from reaching
a final place. With no loss of generality, we assume
that an exception (raised at some moment throughout
the execution) that is not managed by the workflow,
forces the running activities that monitor the excep-
tion not to terminate. Under such assumption, the ter-
mination of an execution, and then of all the activities
occurring therein, can only be guaranteed if end is
reached. However, the assumption does not prevent
modelling an activity, say a, that terminates with an
error configuration. In fact, one can introduce an ex-
ception to represent the wrong termination of a and a
special activity that detects it and that is specifically
devised for managing faulty termination of a. In ad-
dition, workflow executions are not restricted only to
finite paths (from start to end) and infinite iterations
of finite paths of the workflow are still allowed. In
fact, infinite executions are representative of wrong
behaviours only when there is one (ore more) activity,
over some paths, that can not terminate and does not
allow the workflow to proceed further and reach end.
To guarantee that a workflow is correctly designed,
all the exceptions that may raise during an execution
have to be caught and solved. Designers should pre-
vent anomalous situations by defining suitable recov-
ery actions that restore the workflow execution.
We assume that the set of exceptions associated
with a workflow is partitioned into the set of per-
manent (i.e., non-punctual) exceptions and the set of
punctual exceptions. Informally, we say that an ex-
ception is punctual when its duration is negligible,
whereas we say that an exception is non-punctual
when it may have a duration and it lasts from a posi-
tion where it is raised until a position where it expires.
Each activity a ∈ A can be associated with three, pos-
sibly empty, sets of exceptions. Set throw(a) is the
set of exceptions that activity a can notify whenever a
potential dangerous error may compromise the work-
flow execution and that have to be suitably handled by
some other activity which is able to repair the fault.
Set catch(a) contains exceptions that activity a can
handle, that is, that the activity may take on responsi-
bility of remedying the fault. Set probe(a) is the set
of exceptions that may compromise the workflow ex-
ecution because they let activity a switch to an error
state, if no activity catching them is active at the same
time.
In Section 3, we define formally, through LTL for-
mulae, the semantics of correct workflows executions
with respect to the specific semantics of conditional
cases and split-join activities and recovery exceptions.
The case study approached in this paper is de-
picted in Figure 1 and describes a typical office work-
ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends
32

flow for order processing that is commonly found in
large and medium-sized organizations (for more de-
tails (Ellis et al., 1995)). Although the example may
appear too simple, most of the online purchase sys-
tems are actually of comparable complexity, apart ab-
stracting from several details. The workflow we pro-
vide is a simple example of wrong design as some
exceptions are handled incorrectly and may cause in-
finite executions. To demonstrate the effectiveness
of our approach, in Section 4, we verify (the LTL
model of) the workflow and we show that discover-
ing wrong executions allows us to enforce model re-
finement and obtain a correct design. The workflow
consists of the ten activities, depicted within rectan-
gles, and is endowed with two permanent exceptions
HF (Hardware Failure), SF (Software Failure) and
one punctual exception TF (Transport Failure). An
ingoing arrow into an activity labelled with excep-
tions defines the set probe of the activity while an
outgoing arrow, labelled with exceptions, defines the
set throw. We have throw(InternalCreditCheck) =
{HF, SF} and throw(Shipping) = {TF}. The set of
exceptions that an activity catches is defined within
square brackets and it is written beside the name of the
activity in the rectangle. We have catch(Recovery) =
{SF} and catch(Reject
2
) = {TF}. Conditional cases
are graphically represented by diamonds, and labelled
with ? and SF recovery. Split-join activities are de-
picted by diamonds labelled with k.
3 FORMAL SEMANTICS
LTL (Lichtenstein et al., 1985) is one of the most pop-
ular descriptive language for defining temporal be-
haviours that are represented as sequences of observa-
tions. The time model adopted in this logic is a totally
ordered set (e.g., (N, <)) whose elements are the po-
sitions where the behaviour is observed. LTL allows
the expression of positional orders of events both to-
wards the past and the future. Let AP be a finite set of
atomic propositions. Well-formed LTL formulae are
defined as follows:
φ :=
p | φ ∧ φ | ¬φ | X (φ) | Y(φ) | φUφ | φSφ
where p ∈ AP, X, Y, U and S are the usual “next”,
“previous”, “until” and “since” modalities. The dual
operator “release” R is defined as usual, i.e., φRψ is
¬(¬φU¬ψ). Useful operators can be defined from
the previous ones. “Eventually” is defined as F(φ) =
trueUφ and “Globally" Gφ operator is falseRφ. In-
formally, F (φ) means that φ will eventually occur in
the future, including the current position, and G (φ)
means that φ holds indefinitely from the current posi-
tion.
Order Receipt
Inventory Check
Reject 1
Internal Credit Check
YES
NO
SF
HF
SF recovery?
NO
YES
Recovery [SF]
?
Reject 2 [TF]
NO
YES
II
Billing Shipping
II
Archiving
Confirmation
TF
HF
HF
SF
TF
Figure 1: Workflow Case Study.
The semantics of LTL formulae is defined with re-
spect to a strict linear order representing time (N, <).
Truth values of propositions in AP are defined by in-
terpretation π : N →℘(AP) associating a subset of the
set of propositions with each element of N. The se-
mantics of a LTL formula φ at instant i ≥ 0 over a
linear structure π is recursively defined as in Table 1,
Table 1: Semantics of LTL.
π, i |= p ⇔ p ∈ π(i) for p ∈ AP
π, i |= ¬φ ⇔ π, i 6|= φ
π, i |= φ ∧ ψ ⇔ π, i |= φand π, i |= ψ
π, i |= X (φ) ⇔ π, i + 1 |= φ
π, i |= Y (φ) ⇔ π, i − 1 |= φ ∧ i > 0
π, i |= φUψ ⇔ ∃ j ≥ i : π, j |= ψ ∧ π, n |= φ ∀ i ≤ n < j
π, i |= φSψ ⇔ ∃0 ≤ j ≤ i : π, j |= ψ ∧ π, n |= φ ∀ j < n ≤ i
A formula φ ∈ LTL is satisfiable if there exists an
interpretation π such that π, 0 |= φ.
AnLTLSemanticsofBusinessWorkflowswithRecovery
33
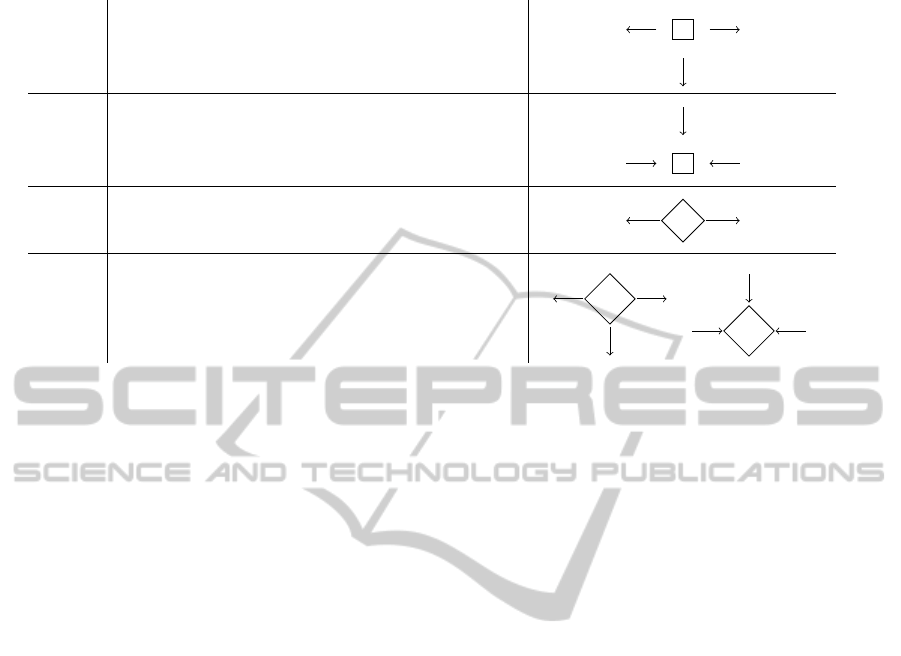
Table 2: Workflow LTL encoding. For convenience, transitions are labeled with numeric pedices.
[a]
t
out
(a)
a ⇒ (a ∧ ¬t
out
(a))U(t
out
(a)) ∨ G (a) (1)
^
t∈out(a)
(t ⇒ Y(a) ∧ ¬a) (2)
a
t
2
t
1
t
i
t
in
(a)
[a]
a ⇒ (a ∧ ¬t
in
(a))S(t
in
(a)) (3)
^
t∈in(a)
(t ⇒ X(a) ∧ ¬a) (4)
a
t
2
t
1
t
i
[· + ·]
t
1
⇒ ¬t
2
(5)
⊕ ⇒ ¬Y(⊕) ∧ ¬X (⊕) (6)
+
t
1
t
2
[· | ·]
^
t
1
,t
2
∈out(k)
(t
1
⇔ t
2
) or
^
t
1
,t
2
∈in(k)
(t
1
⇔ t
2
) (7)
k ⇒ ¬Y(k) ∧ ¬X (k) (8)
k
t
2
t
1
t
i
k
t
2
t
1
t
i
Workflow Model
Workflows model execution of systems as sequences
of activities. Transitions, conditional case and split-
join interleave the activities and determine uniquely
the execution flow, i.e., the sequence of activities that
realizes the computation. An activity is an abstrac-
tion of a compound of actions that are performed by
the real workflow. Although they can be modelled
as atomic computations, we adopt a different per-
spective for which the activities, being actions in the
real world, have a non-punctual duration. To trans-
late workflows into an LTL formula, we assume that
all the activities (except for the activities start and
end) are always followed by a transition, and vicev-
ersa, and that conditional case and split-join are spe-
cial activities that have punctual duration. When an
activity is performed, the firing of the outgoing tran-
sition lets the system change allowing it to execute
the next activity. Therefore, our LTL translation al-
lows modelling of workflows as sequences of activi-
ties and transitions, in strict alternation.
Let (A,T ) be a workflow. With no loss of general-
ity, we assume that no element in the graph is dupli-
cated. By this assumption, we associate each activity
with an atomic proposition that uniquely identifies it.
We write t
pq
to indicate an element (p, q) ∈ T , i.e., a
transition between activities p, q ∈ A. If activity a ∈ A
holds at position i then the workflow is performing ac-
tivity a at that position; similarly for t. We introduce
k and ⊕ to indicate a split-join activity and a condi-
tional case activity, respectively; start and end to indi-
cate the starting and the final activity of the workflow.
Workflow diagrams are translated according to rules
in Table 2.
Let t
out
(a) be the disjunction
W
t∈out(a)
t and t
in
(a)
be the disjunction
W
t∈in(a)
t.
Formula (1) states that if activity a holds at the
current position, then it is true, at that position, that
either a holds forever, which is the case of a work-
flow that is blocked because of an exception, or a but
not t
out
(a) holds until at least one transition in out(a)
holds. In this way, activity a lasts until one of its
outgoing transition fires. Formula (2) imposes that
if transition t
i
∈ out(a) holds at position i, then in the
previous one i − 1, activity a holds. This necessary
condition enforces that a transition fires only if the
activity from which it originates has just been termi-
nated.
Formula (3) states that if activity a holds at the
current position, then it is true, at that position, that
a but not t
in
(a) holds since at least one transition in
in(a) has been fired. In this way, activity a has lasted
since one of its ingoing transition fired. Formula (4)
imposes that if transition t ∈ in(a) holds at position i,
then, in the next one i + 1, activity a holds. This nec-
essary condition enforces that a transition fires only if
the activity to which it leads will be performed in the
next position.
Given an activity a ∈ A, the LTL semantics that
we associated with [a]
t
out
(a)
and
t
in
(a)
[a] does not im-
pose any constraint on the firing of transitions in the
sets out(a) and in(a), making the execution flow non-
deterministically determined. In fact, formulae (1)-
(4) only state that the execution following activity a
is realized by some (at least one) transitions of out(a)
that fire when a terminates and, symmetrically, that
the execution preceding a lets some (at least one) tran-
sitions of in(a) fire to start the execution of a.
Conditional case [· + ·] and split-join [· | ·] ac-
tivities are modelled by using the formulae (1)-(4)
ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends
34

and, in addition, specific constraints which enforce
the proper execution flow. To model the flow of the
conditional cases, we force the execution of the two
branches to be exclusive as for the if-then-else con-
struct of programming languages. The translation of
the split (resp. join) activity is similar yet it enforces
the synchronization of all the transitions starting from
(resp. yielding to) it.
The conditional case [· | ·] is translated composi-
tionally. For each conditional activity we introduce a
new fresh atomic proposition ⊕. Formulae (1), (2),
(3) and (4) define the semantics of the activity and
Formula (5) imposes the uniqueness of the execution,
i.e., that only one branch is executed, by requiring
the strict complementarity between t
1
and t
2
. Formula
(6) enforces the punctuality of ⊕ and states that, if ⊕
holds at position i then, in the next and in the previous
positions, it does not hold.
The translation of the split-join activities is similar
to the one defined for the conditional case. For each
split-join activity we introduce a new fresh atomic
proposition k and we use formulae (1), (2), (3) and (4)
to define the semantics of the activity and Formula (6)
to enforce the punctuality of k, similarly to the previ-
ous case. Formula (7) is divided into two parts that are
used exclusively. Both of them impose strict contem-
poraneity of all the transitions associated with activity
k. The first one, on the left side, is only defined for the
split activity and states that all the outgoing transitions
starting from it, occur at the same time. The second
one, on the right side, is similar but it is defined for
the join activity, where all the parallel computations
must join before proceeding further. It states that all
the ingoing transitions, leading to it, occur at the same
time.
We assume that when a workflow terminates, it
never resumes, by adding to the model formula end ⇒
G(end). The assumption is realistic because business
process executions are unique, always have a start-
ing point, where inputs are collected and fed to the
process, and possibly terminate by producing an out-
come. Infinite repetitions of finite (correct) execu-
tions of a workflow are not meaningful for our pur-
pose as our intention aims at modelling infinite ex-
ecutions only when they represent wrong exception
handling.
Encoding Exceptions
Let E be a (finite) set of exceptions associated with
the workflow and P and S be two subsets of E such
that P ∪ S = E and P ∩ S =
/
0 where P is the set of
permanent exceptions and S is the set of punctual ex-
ceptions. In this section, with abuse of notation, we
restrict set A only to activities that are not start, end,
split-join and conditional activities with which no ex-
ception is associated.
Informally, we say that an exception is punctual
when it holds exactly one time instant whenever it oc-
curs. Conversely, an exception is non-punctual when
it may have a duration and it lasts from a position
where it is raised until a position where it expires. Let
s ∈ S. To model punctual exception s we introduce
the following Formula (9) that forces exception s to
be false in the next position of the one where excep-
tion s occurs.
^
e∈S
(e ⇒ ¬X(e)) (9)
Let a be an activity and catch(a) be the set of ex-
ceptions that activity a can restores. Non-punctual ex-
ceptions may hold continuously over some adjacent
positions. When such an exception occurs, at some
position, then it holds until an activity a such that
e ∈ catch(a) restores the exception. The following
Formula (10) states that if, at the current position, e
holds then there is a position in the future where an
activity restores it, otherwise it will hold indefinitely.
In fact, the consequent of the implication imposes that
if
W
a:e∈catch(a)
(eUa) holds then ¬G (e) must hold,
that is, e will not hold indefinitely. Conversely, if
W
a:e∈catch(a)
(eUa) does not hold then ¬G (e) must not
holds, that is, e will hold indefinitely.
^
e∈P
(e ⇒ (¬G(e) ⇔
_
a∈A
e∈catch(a)
(eUa)) (10)
Let probe(a) be the set of exceptions associated
with activity a that may let a loop indefinitely. If a is
active at a certain position of the time, then the occur-
rence of an exception e in probe(a) causes an abor-
tion of a if, at that moment, there is no activity b that
restores e, such that e ∈ catch(b). The abortion repre-
sents a configuration of error that can not be restored,
i.e., a loops infinitely or terminates with a system er-
ror. Formula (11) states that, if at the current position,
activity a holds and exception e occurs and no activity
managing e is active, i.e., e ∈ catch(b), then activity a
will never terminate.
^
e∈probe(a)
(a ∧ e ∧
^
b∈A
e∈catch(b)
¬b) ⇒ G(a) (11)
Formula (11) is defined for all activities a ∈ A of the
workflow with a non empty set probe(b).
Following Formulae (12) and (13) define the nec-
essary conditions to have infinite execution. For-
mula (12) is specific for punctual exceptions. At a
certain position, if activity a is active and it never ter-
minates, i.e., G (a) holds at that position, then there
exists an activity c of the workflow, possibly different
AnLTLSemanticsofBusinessWorkflowswithRecovery
35

from a, that eventually loops indefinitely because an
exception e ∈ probe(c) is not correctly handled. This
allows modelling the fact that an infinite execution of
an activity may be enforced by a different activity that
goes into an error state. Moreover, the faulty activity
c may start its execution when activity a is already
running and the occurrence of the exception that in-
duces the infinite looping error state of c may occur
even later its starting position. This explains the F in
the consequent of the formula that holds when there
is a position i, possibly following the position where
G(a) begins to hold, such that, from that position i,
there is a position in the past throughout the execu-
tion of c where an exception e ∈ probe(c) occurred
and no activity managing e was active.
G(a) ⇒ F
_
c∈A
(c)S(c ∧
_
e∈probe(c)
(e ∧
^
b∈A
e∈catch(b)
¬b))
(12)
Formula (12) does not apply to non-punctual excep-
tion because S may hold only in one position (and this
is enough to have G (a)) because non-punctual excep-
tions are not forced to hold indefinitely when no activ-
ity of the workflow can eventually handle them. Next
Formula (13) remedies the problem and requires that
if activity a holds forever, then there is an activity c
(which may possibly be a) and a non-punctual excep-
tion e ∈ probe(c) that holds indefinitely, because no
activity b ever catches e.
G(a) ⇒ F
_
c∈A
e∈probe(c)
G
c ∧ e ∧
^
b∈A
e∈catch(b)
¬b)
(13)
Both formulae (12) and (13) are defined for all activ-
ities a ∈ A appearing in the workflow. Observe that
when probe(c), for some c ∈ A, is empty then the sec-
ond formula of S, in Formula (12), and the formula
within F, in Formula (13), are trivially false. In this
case, the activity appearing in the antecedent of the
formula always terminates and no looping executions
are admitted for it, because G(a) is false.
An exception e ∈ E is internal if it is thrown by
some activity appearing in the workflow whereas it
is external otherwise. Next Formula (14) defines the
necessary condition so that an internal exception is
thrown. Let throw(a) be the set of exceptions that
activity a may rise. The first formula states that if ex-
ception e ∈ S holds then there exists an activity a that
is active at the same position such that e belong to the
set of exceptions which a can raise, i.e., e ∈ throw(a).
The second formula requires that if a permanent ex-
ception e holds then there is an activity b and a posi-
tion in the past where b raised e.
^
e∈S
(e ⇒
_
a∈A
e∈throw(a)
a)
^
e∈P
(e ⇒ (e)S(e ∧
_
b∈A
e∈throw(b)
b)).
(14)
Next Formula (15) defines the necessary condition for
external exceptions. The first part imposes that an ex-
ternal punctual exception e occurs when at least one
activity of A is underway. This guarantees that the ex-
ception can not happen in correspondence of positions
where only transitions hold (and special activities) be-
cause transitions are assumed to have no real duration.
The second part is similar to the first one and requires
that when an external non-punctual exception occurs
then there is an activity that is active at some position
in the past. In fact, a non-punctual exception may
be active even in some positions, between the current
one and the one where the exception was generated,
where no activity of the workflow is performed. We
require however that an exception raises when at least
one activity is active (again to avoid meaningless oc-
currences one temporal unit long, in correspondence
of positions where only transitions hold).
^
e∈S
(e ⇒
_
a∈A
a)
^
e∈P
(e ⇒ (e)S(e ∧
_
a∈A
a)).
(15)
We can now, formally, define the executions of a
workflow. Let W be a workflow and φ
W
the LTL for-
mula translating W that is defined by conjunction the
formulae above, globally quantified over the time. We
define execution of W an LTL interpretation π for for-
mula φ
W
such that π, 0 |= φ
W
.
4 EXPERIMENTAL RESULTS
With the introduction of exceptions, designers can
represent different scenarios by specifying and ver-
ifying functional properties and controlling the be-
haviour of a workflow when different kinds of ab-
normal behaviours occur. In this section, some ex-
amples of such type of LTL functional properties are
defined and analysed (referring to the workflow of
Figure 1). The objective is showing the usefulness
of the LTL based-semantics approach and how it can
be used in practical cases when abnormal behaviours
do exist. With the approach shown in this paper, a
formal demonstration of correctness does not make
ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends
36

⊕ ⇒ (⊕ ∧ ¬(t
yes
∨t
no
))U(t
yes
∨t
no
))
t
yes
⇒ Y(⊕) ∧ ¬⊕
t
no
⇒ Y(⊕) ∧ ¬⊕
t
yes
⇒ ¬t
no
⊕ ⇒ ¬Y(⊕) ∧ ¬X (⊕)
k
start
⇒ (k
start
∧ ¬t
yes
)S t
yes
t
yes
⇒ X(k
start
) ∧ ¬k
start
k
start
⇒ (k
start
∧ ¬(t
1
∨t
2
))U(t
2
∨t
2
))
t
2
⇒ Y(k
start
) ∧ ¬k
start
t
1
⇒ Y(k
start
) ∧ ¬k
start
t
1
⇔ t
2
k
start
⇒ ¬Y(k
start
) ∧ ¬X (k
start
)
Bill ⇒ (Bill ∧ ¬t
1
)S t
1
t
1
⇒ X(Bill) ∧ ¬Bill
Bill ⇒ (Bill ∧ ¬t
1
)U t
3
t
3
⇒ Y(Bill) ∧ ¬Bill
(Bill ∧ tf ∧ ¬Reject
2
) ⇒ G(Bill)
(hf ⇒ (¬G(hf ) ⇔ false)
(sf ⇒ (¬G(sf ) ⇔ (sf )U(Recovery))
G(Bill) ⇒ F ((Bill)S(Bill ∧ (tf ∧ ¬Reject
2
))
G(Bill) ⇒ F
G(Bill ∧ hf )∨
G(Bill ∧ sf ∧ ¬Recovery)∨
G(Ship ∧ hf )
Bill ∧ sf ∧ ¬Recovery ⇒ G (Bill)
tf ⇒ ¬X(tf )
tf ⇒ Ship
Bill ∧ hf ⇒ G (Bill)
Figure 2: Some formulae modelling the portion of workflow in Figure 1. All formulae are conjuncted (symbol ∧ is omitted for
brevity) and globally quantified over time by G. Observe that, since the workflow does not have an activity catching exception
hf , whenever it occurs at the same time as activity Bill then Bill enters in an error state, i.e., infinite looping.
sense, since a semantics of business workflows is pre-
cisely what is being introduced. At the end of the sec-
tion, we present an analysis of the results in terms of
performances of the verification process and satisfia-
bility of properties. For the sake of brevity, we only
report a partial translation of the workflow depicted
in Figure 1, starting from the second conditional case
marked with a symbol ?.
We introduce the following atomic propositions to
represent activities: ⊕ for modelling the conditional
block, k
start
and k
end
for activities defining starting
and ending point of the join block and Bill for Billing.
Similarly, we introduce a proposition for all other ac-
tivities. We use t
1
to indicate the transition reaching
Billing which starts from k
start
and t
2
to indicate the
transition reaching Shipping which starts from k
start
.
Finally, we use sf , hf and tf to model exceptions Soft-
wareFailure, HardwareFailure and TransportFailure.
Formulae in the first row of Figure 2 are the transla-
tion of the conditional case, the split-join and Billing
activities.
To validate the LTL model, we exploit the
Bounded Satisfiability Checking (BSC) (Pradella
et al., 2013) approach. Other approaches are of
course possible, like the traditional non-symbolic
LTL Model Checking based on the construction of
classical Büchi automata (Vardi and Wolper, 1986).
The key idea behind BSC is to build a finite represen-
tation, of length k, of an infinite ultimately periodic
LTL model of the form αβ
ω
, where α and β are fi-
nite words over the alphabet 2
AP
. BSC tackles the
complexity of checking the satisfiability for LTL for-
mulae by avoiding the unfeasible construction of the
Büchi automata. (Bersani et al., 2011) proves that
BSC problem for LTL and its extension is complete
and that it can be reduced to a decidable Satisfiability
Modulo Theory (SMT) problem.
All tests were carried out by using Zot and Mi-
crosot Z3 SMT solver (Microsoft Research, 2009).
However, it is also possible to perform analy-
sis with other model checkers that take LTL as
their input modelling language. Zot is a Bounded
Model/Satisfiability checker, written in Lisp, that
takes as input specifications written in a variety of
temporal logics, and determines whether they are sat-
isfiable or not. It performs the checks by encoding
temporal logic formulae into the input language of
various solvers, in particular SAT and SMT solvers.
SAT solvers are capable of taking, as input, formulae
written in propositional logic. SMT solvers instead
accept formulae written in logics (fragments of First-
Order Logic) that are richer than the simple proposi-
tional one. Suitable modules, interface Zot with the
underlying SAT or SMT solvers. Zot scripts, which
contain both the model to be analysed and the nec-
essary commands to invoke the desired solver, are a
collection of Lisp statements.
Table 3 shows time – in seconds – required by Zot
to verify the set of functional user-defined properties,
memory occupation – in MBytes – and the result, i.e.
whether the property is satisfied or not. Let S be the
formula which translates the model of our workflow
in Figure 1. If S is fed to Zot "as is", Zot will look
for one of its execution; if it does not find one – i.e.,
if the model is unsatisfiable – then our translation is
contradictory, hence it contains some flaws. Now, let
P be one of the LTL formulae which model one of the
functional properties we want to check on the work-
AnLTLSemanticsofBusinessWorkflowswithRecovery
37

flow. If S ∧ ¬P is unsatisfiable, this means that there
is no execution that satisfies the workflow, that also
satisfies ¬P, that is, that violates the property P, so
P holds; otherwise this means that there is at least
one execution that satisfies both S and ¬P; that is,
there is at least one execution of the workflow that
violates the property, so the property does not hold.
If Zot determines that a formula is satisfiable, then
the tool produces an execution that satisfies it that de-
signer can use to check the correctness of the mod-
elling, i.e. a counterexample trace that is compatible
with the workflow model but that violates the prop-
erty.
We now provide the LTL formulae of the proper-
ties that we have considered for verifing the workflow
of Figure1.
G(¬tf ∧ ¬hf ∧ ¬sf ) ⇒ F (end) (16)
Formula (16) states that, if no exceptions occur,
the workflow must terminate. Feeding the model
checker with the negation of this property and the LTL
model of the workflow, we can check if all possible
executions of the workflow reach end state. As re-
ported in Table 3, the property holds, since there are
no traces which satisfy its negation.
(G(¬tf ∧ ¬sf ) ∧ F (hf )) ⇒ F(end) (17)
(G(¬hf ∧ ¬sf ) ∧ F (tf )) ⇒ F(end) (18)
Formula (18) is similar to formula (17), except
that it checks the occurrence of the TransportFailure
punctual exception, which is thrown by Shipping ac-
tivity and models a shipping problem, such as a truck
accident. As reported in Table 3, property (18) does
not hold: the counterexample trace shows again that
the activities Billing and Shipping loop forever. Hav-
ing a look at the workflow, we can note that the prob-
lem comes from the exception tf being caught inside
the wrong activity, Reject2, which is not executed in
parallel with Shipping.
F(G (Bill)) ⇔ F(G (Ship)) (19)
F(G (Bill)) ⇔ F(G (Arch)) (20)
Formulae (19) and (20) model different type of
properties respect to the other ones: Formula (19)
states that activity Billing loops forever if and only
if activity Shipping do the same, while Formula (20)
states the same for the activities Billing and Archiv-
ing. Ship and Arch are the abbreviations respectively
of Shipping and Archiving. Table 3 shows that the
property modeled by Formula (19) holds, while the
other one does not hold: in fact, analysing the coun-
terexample trace and the workflow, we can note that
if activity Billing loops forever, it is not possible to
reach activity Archiving.
All tests have been carried out on a 3.3 Ghz quad
core PC with 16 Gbytes of RAM. The bound k, which
is a user-defined parameter representing the maximal
length of runs analysed by Zot, corresponds to the
number of discrete positions that are used to build the
bounded representation of the model. The value cho-
sen is k = 35. By analysing the longest path of the
workflow of Figure 1, one can see that this value for k
is big enough to guarantee the definition of meaning-
ful workflow executions, i.e., interpretations over the
symbols appearing in the workflow that are model of
the LTL formula translating it (partly shown in Fig-
ure 2 and defined through rules of Section 3).
Table 3: Test results.
Formula Time (s) Memory (Mb) Result
Formula (16) 2.836 16 UNSAT
Formula (17) 3.883 60 SAT
Formula (18) 3.443 60 SAT
Formula (19) 3.843 60 UNSAT
Formula (20) 3.785 60 SAT
Resources (in terms of time and memory) needed
to perform the analysis are limited despite the facts
that the size of the LTL model is not trivial. In particu-
lar, to verify properties like the ones modelled by For-
mulae (16) and (19), Zot must exhaustively analyse
all possible runs to return UNSAT, which is the worst
case in terms of time and memory consumed; taking
it into account, we can conclude that it is feasible,
using modern model checking tools such as Zot, to
perform formal verification of non-trivial functional
properties, in a limited amount of resources, allow-
ing designer to execute the analysis in an interactive
real-time manner.
We left as future work the implementation and
testing of more interesting properties, such as hard
real-time properties.
5 CONCLUSIONS AND FUTURE
WORK
The major objective of this paper is demonstrating
how temporal logics are effective in giving seman-
tics and iteratively enforce requirements into the pro-
cess. Our approach is lightweight and allows the reuse
of existing tool support. The working assumption is
that a lightweight solution would easily fit into pro-
cesses that are already in place without the need for
ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends
38

a radical change of procedures, tools and people’s at-
titudes. The complexity of formalisms and invasive-
ness of methods have been indeed demonstrated to be
one of the major drawback and obstacle for deploy-
ment of formal engineering techniques into mundane
projects. The case study is a purchase workflow, but
the results can be extended to other systems with em-
phasis on dependability and abnormal behavior man-
agement. The treatment of exception handling, and
more in general of recovery, is another substantial
contribution that has been less frequently investigated
with similar techniques and tools.
The workflow patterns here analyzed are limited
with respect to a real scenario. Workflow patterns as
presented in (van der Aalst et al., 2003) need to be in-
vestigated and encoded. Once workflows are intended
as graphs and transitions are treated like in this paper,
similarities emerge with the Petri Nets approach, in
particular with Workflow Petri Nets (Aalst, 1997).
Future work aims at extending the current trans-
lation of workflows by using more expressive logics.
In particular, we plan to extend the basic definition of
workflow by adding timing constraints on activities
and transitions. To model timed workflow we may ex-
ploit CLTLoc (Bersani et al., 2013), which is an LTL
based logic where atomic formulae are both atomic
propositions and constraints over dense clocks. Zero-
time modelization is also an open issue. When some
workflow activities have a negligible duration with re-
spect to the other ones, they may be modeled as hav-
ing a logical zero time duration. This implies Zeno
behaviours and other counterintuitive consequences.
(Ferrucci et al., 2012) introduces a new metric tempo-
ral logic called X-TRIO, which exploits the concepts
of Non-Standard Analysis (Robinson, 1996). The way
to "glue" together CLTLoc with X-TRIO is a promis-
ing research strand.
BPMN (OMG, 2011) is the one of the most
widespread technique to model business workflows.
In (Mazzara and Dragoni, 2012) it has been exploited
for workflow design, which has then been imple-
mented in WS-BPEL. In particular, BPMN (as well
as UML activity diagrams) includes the concept of
partition (modeled as pools and swimlanes), that is
essential for business processes modeling and which
has not been considered here. This will need to be
investigated later.
Finally, runtime evolution in business processes
(Baresi et al., 2014) and, more in general, the idea
of self-reconfiguring systems are related issues we in-
tend to further explore.
ACKNOWLEDGEMENTS
The authors acknowledge the support and advice
given by Anirban Bhattacharyya, Alexandr Naum-
chev, Miticus Flamejante, Vínicius Pereira, Diego
Pérez, Michele Ciavotta, Marco Miglierina and all the
other Friends at Politecnico di Milano, which repre-
sent a moving force, an actual égrégore capable of
always moving ideas forward to the next level.
REFERENCES
Aalst, W. M. P. v. d. (1997). Verification of workflow nets.
In Proceedings of the 18th International Conference
on Application and Theory of Petri Nets, ICATPN ’97,
pages 407–426, London, UK, UK. Springer-Verlag.
Attie, P. C. and Singh, M. P. (1993). Specifying and enforc-
ing intertask dependencies. In In Proceedings of the
19th VLDB Conference, pages 134–145.
Augusto, J. C., Howard, Y., Gravell, A. M., Ferreira, C.,
Gruner, S., and Leuschel, M. (2003). Model-based
approaches for validating business critical systems. In
STEP, pages 225–233.
Baier, C. and Katoen, J.-P. (2008). Principles of Model
Checking. MIT Press.
Baresi, L., Guinea, S., and Manna, V. P. L. (2014). Consis-
tent runtime evolution of service-based business pro-
cesses. In Anna Liu, John Klein, A. T., editor, Work-
ing IEEE/IFIP Conference on Software Architecture
(WICSA).
Baresi, L., Morzenti, A., Motta, A., and Rossi, M. (2012).
A logic-based semantics for the verification of multi-
diagram uml models. ACM SIGSOFT Software Engi-
neering Notes, 37(4):1–8.
Bersani, M. M., Frigeri, A., Rossi, M., and San Pietro, P.
(2011). Completeness of the bounded satisfiability
problem for constraint LTL. In Reachability Prob-
lems, volume 6945 of LNCS, pages 58–71.
Bersani, M. M., Rossi, M., and San Pietro, P. (2013). A tool
for deciding the satisfiability of continuous-time met-
ric temporal logic. In Proceedings of the International
Symposium on Temporal Representation and Reason-
ing (TIME), pages 99–106.
Butler, M. J. and Ferreira, C. (2004). An operational seman-
tics for stac, a language for modelling long-running
business transactions. In Nicola, R. D., Ferrari, G. L.,
and Meredith, G., editors, COORDINATION, volume
2949 of Lecture Notes in Computer Science, pages
87–104. Springer.
Calzolai, F., Nicola, R. D., Loreti, M., and Tiezzi, F. (2008).
Tapas: A tool for the analysis of process algebras. T.
Petri Nets and Other Models of Concurrency, 1:54–
70.
Díaz, M., Valero, V., Macía, H., Mateo, J., and Díaz, G.
(2012). Bpel-rf tool: An automatic translation from
ws-bpel/wsrf specifications to petri nets. In ICSEA
2012 : The Seventh International Conference on Soft-
ware Engineering Advances.
AnLTLSemanticsofBusinessWorkflowswithRecovery
39

Dragoni, N. and Mazzara, M. (2009). A formal semantics
for the ws-bpel recovery framework - the pi-calculus
way. In Laneve, C. and Su, J., editors, WS-FM,
volume 6194 of Lecture Notes in Computer Science,
pages 92–109. Springer.
Eisentraut, C. and Spieler, D. (2009). Web services and for-
mal methods. chapter Fault, Compensation and Ter-
mination in WS-BPEL 2.0 – A Comparative Analysis,
pages 107–126. Springer-Verlag, Berlin, Heidelberg.
Ellis, C., Keddara, K., and Rozenberg, G. (1995). Dy-
namic change within workflow systems. In Proceed-
ings of Conference on Organizational Computing Sys-
tems, COCS ’95, pages 10–21, New York, NY, USA.
ACM.
Eshuis, R. and Wieringa, R. (2002). Verification support for
workflow design with uml activity graphs.
Ferrucci, L., Mandrioli, D., Morzenti, A., and Rossi, M.
(2012). A metric temporal logic for dealing with zero-
time transitions. In Proc. of 19th International Sym-
posium on Temporal Representation and Reasoning,
pages 81–88. IEEE Computer Society.
Foster, I., Frey, J., Graham, S., Tuecke, S., Czajkowski, K.,
Ferguson, D., Leymann, F., Nally, M., Storey, T., and
Weerawaranna, S. (2004). Modeling stateful resources
with web services.
Ghezzi, C., Mandrioli, D., and Morzenti, A. (1990). Trio:
A logic language for executable specifications of real-
time systems. J. Syst. Softw., 12(2):107–123.
Gmehlich, R., Grau, K., Iliasov, A., Jackson, M., Loesch,
F., and Mazzara, M. (2013). Towards a formalism-
based toolkit for automotive applications. In Formal
Methods in Software Engineering (FormaliSE).
Harel, D. (1987). Statecharts: a visual formalism for com-
plex systems. Science of Computer Programming,
8(3):231 – 274.
Lichtenstein, O., Pnueli, A., and Zuck, L. (1985). The glory
of the past. In Proc. of Logics of Programs, volume
193 of LNCS, pages 196–218. Springer.
Lucchi, R. and Mazzara, M. (2007). A pi-calculus based
semantics for ws-bpel. Journal of Logic and Algebraic
Programming, 70(1):96–118.
Mazzara, M. (2009). Deriving specifications of dependable
systems: toward a method. In 12th European Work-
shop on Dependable Computing (EWDC).
Mazzara, M. (2011). On methods for the formal specifica-
tion of fault tolerant systems. In Proceedings of the
4th International Conference on Dependability (DE-
PEND 2011).
Mazzara, M. and Bhattacharyya, A. (2010). On modelling
and analysis of dynamic reconfiguration of depend-
able real-time systems. DEPEND, International Con-
ference on Dependability.
Mazzara, M. and Dragoni, Nicola Zhou, M. (2012). Imple-
menting workflow reconfiguration in ws-bpel. Jour-
nal of Internet Services and Information Security,
2(1/2):73–92.
Microsoft Research (2009). Z3: An efficient SMT
solver. Available at: http://research.microsoft.com/en-
us/um/redmond/projects/z3/.
Montesi, F., Guidi, C., and Zavattaro, G. (2014). Service-
oriented programming with jolie. In Web Services
Foundations, pages 81–107.
Morzenti, A. and San Pietro, P. (1994). Object-oriented
logical specification of time-critical systems. ACM
Transactions on Software Engineering and Methodol-
ogy (TOSEM), 3(1):56–98.
OASIS (2007). Web services business process ex-
ecution language version 2.0. http://docs.oasis-
open.org/wsbpel/2.0/wsbpel-v2.0.pdf.
OMG (2005). Unified modeling language 2.0.
http://www.omg.org/spec/UML/2.0/.
OMG (2011). Business process model and notation (bpmn).
http://www.bpmn.org/.
Pradella, M., Morzenti, A., and San Pietro, P. (2008). Refin-
ing real-time system specifications through bounded
model- and satisfiability-checking. In ASE, pages
119–127.
Pradella, M., Morzenti, A., and San Pietro, P. (2013).
Bounded satisfiability checking of metric temporal
logic specifications. ACM Trans. on Soft. Eng. and
Meth. (TOSEM).
Robinson, A. (1996). Non-standard analysis. Princeton
University Press.
Romanovsky, A. and Thomas, M., editors (2013). In-
dustrial Deployment of System Engineering Methods.
Springer.
van der Aalst, W., ter Hofstede, A., Kiepuszewski, B., and
Barros, A. (2003). Workflow patterns. Distributed and
Parallel Databases, 14(1):5–51.
Vardi, M. Y. and Wolper, P. (1986). An automata-theoretic
approach to automatic program verification. In Proc.
of LICS, pages 332–344.
Vaz, C. and Ferreira, C. (2012). On the analysis of
compensation correctness. J. Log. Algebr. Program.,
81(5):585–605.
Yamaguchi, M., Yamaguchi, S., and Tanaka, M. (2009). A
model checking method of soundness for workflow
nets. IEICE Transactions, 92-A(11):2723–2731.
ICSOFT-PT2014-9thInternationalConferenceonSoftwareParadigmTrends
40
