Distributed Parallel Algorithm for Numerical Solving of 3D Problem of

Fluid Dynamics in Anisotropic Elastic Porous Medium Using

MapReduce and MPI Technologies

Madina Mansurova, Darkhan Akhmed-Zaki, Matkerim Bazargul and Bolatzhan Kumalakov

Faculty of mechanics and mathematics, al-Farabi Kazakh National University, al-Farabi ave. 71, Almaty, Kazakhstan

Keywords:

MapReduce, MPI, Distributed-parallel Computing.

Abstract:

Paper presents an advanced iterative MapReduce solution that employs Hadoop and MPI technologies. First,

we present an overview of working implementations that make use of the same technologies. Then we de-

ﬁne an academic example of numeric problem with an emphasis on its computational features. The named

deﬁnition is used to justify the proposed solution design.

1 INTRODUCTION

Modern software engineering solutions provide wide

range of tools for numeric modelling. They vary from

commercial data centre platforms to open source clus-

ter software, downloadable from internet. The aim of

this paper is to design a solution that would utilize

cluster resources by organizing MapReduce compu-

tation with the elements of MPI based parallel pro-

gramming.

In order to accomplish this task we ﬁrst identify

key features of the existing solutions in this domain

in Section 2. Then, in Section 3 we, ﬁrst, construct an

academic example of a numeric model that is used to

place the platform into the constraints of a typical iter-

ative algorithm; second, design solution framework;

and ﬁnally, discuss technological considerations and

ways to overcome them. Finally, Section 4 concludes

the paper.

2 REVIEW OF HYBRID

MAPREDUCE AND MPI

SOLUTIONS

The principles of organization of parallel and dis-

tributed computing have been known for a long time

(Chen et al., 1984), (Gropp et al., 1996), (Sunderam

et al., 1994). MPI and MapReduce can be referred

to the most used technologies. MPI technology is the

main instrument for parallel computing, when solving

a wide spectrum of problems.

However, with the increase in the volume of the

data being processed there arises a question of relia-

bility of MPI applications. In recent years the tech-

nologies of distributed computing MapReduce is be-

ing more widely recognized.

Most of the modern research in this ﬁeld are di-

rected to the search for new methods of organiza-

tions of effective parallel and distributed computing

for large-scale problems and resources (Malyshkin,

2010), (Becker and Dagum, 1992), description of

their adequate discrete models with the possibility to

provide high reliability of the systems being devel-

oped. Of no less actuality are the works in the ﬁeld

of research on parallel computing on heterogeneous

and hybrid systems, development of the systems for

designing parallel programs - frame solutions (skele-

ton), systems of veriﬁcation of parallel programming

code and corresponding architectural solutions.

On the other hand, the problems of effective

exploitation of the existing highly performance re-

sources taking into account their heterogeneity have

neither been completely solved (see (Foug

ere et al.,

2005), (D

ıaz et al., 2012) and (Cappello et al., 2005)).

One of the ways of solution is evidently the attraction

of technologies for virtualization of computer sys-

tems and their integration with technologies of par-

allel computing. An even more complex problem

arises, when considering the problems of organization

of reliable systems realizing the distributed (on het-

erogeneous computing resources) high performance

processing of large volume heterogeneous data (Wang

524

Mansurova M., Akhmed-Zaki D., Bazargul M. and Kumalakov B..

Distributed Parallel Algorithm for Numerical Solving of 3D Problem of Fluid Dynamics in Anisotropic Elastic Porous Medium Using MapReduce and MPI

Technologies.

DOI: 10.5220/0005110605240528

In Proceedings of the 9th International Conference on Software Engineering and Applications (ICSOFT-EA-2014), pages 524-528

ISBN: 978-989-758-036-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

and Liu, 2008), (Pandey and Buyya, 2012).

It is to combination of the advantages of paral-

lel, distributed and cloud computing technologies that

the majority of works are devoted (see (Liu and Or-

ban, 2008), (Valilai and Houshmand, 2013) and (Dean

and Ghemawat, 2008)) in view of their special prac-

tical importance. That work describes a construc-

tive approach of hybrid combination of MapReduce

(Fagg and Dongarra, 2000) and MPI (Ng and Han,

1994) for organization of distributed parallel comput-

ing on heterogeneous systems. A general descrip-

tion of MapReduce technology is presented in many

works (Cohen, 2009), (Jin and Sun, 2013) where the

main accent is given to its use for distributed high

performance processing of huge volume of data. The

main problems in this ﬁeld are provision of effective

load balancing to the existing resources and high reli-

ability of the carried out distributed processing of the

data. The main advantage of MapReduce technology

is a well-deﬁned division of the roles of computing

units - to ”mapper” and ”reducer” the determination

of which does not depend on the structure and char-

acteristics of the computing units. Its signiﬁcant dis-

advantage is the complexity of organization of com-

munications between units in the process of computa-

tion.

Creation of hybrid solutions allows using of the

advantages of separate technologies. There exist a

great variety of such solutions. The authors of the

paper (Lu et al., 2011) compare MPI and MapReduce

technologies from the point of view of the system fail-

ure. A numerical analysis is made to study the effect

of different parameters on failure resistance. The au-

thors believe that their research will be useful in an-

swering the question: at what volumes of data it is

necessary to decline MPI and use MapReduce in case

of possible failures of the system. The study of prim-

itives of MPI and MapReduce communications al-

lowed the authors (Mohamed and Marchand-Maillet,

2012) to assert the fact that MPI can give the rise in

performance of MapReduce applications.

The work (Slawinski and Sunderam, 2012) con-

siderable differs from the above presented works in

which MPI technology is built in the environment of

MapReduce. The authors describe the reverse task

- the start of MapReduce applications in MPI en-

vironment. It is pointed out that several additional

MPI functions should be written for full support of

MapReduce.

Nevertheless, many of these functions are, as a

rule, recognized to be important and are developed in

MPI to support other modern paradigms of program-

ming and parallelization. In (Srirama et al., 2011) the

essence of the approach is considered to be division

of implementation of MPI applications to sequence

of computation stages each of which is completed by

the stage of communication. This approach is based

on the conception of adapters distributed in conven-

tional utilities for coordination of the requirements to

applications and platform hardware.

Other applications for adaptation of MapReduce

model to organization of parallel computing are given

in (Matsunaga et al., 2008), (Biardzki and Ludwig,

2009), (Ekanayake et al., 2010) and (Bu et al., 2012).

As a whole, the problems of effective organization

of iterative computing on MapReduce model remain,

especially, the problems of scalability of such algo-

rithms and their adaptation for a wide range of scien-

tiﬁc problems, there are neither rigorous approaches

to provide reliability of such systems.

3 SOLUTION DESIGN AND

IMPLEMENTATION

3.1 Mathematical Model and Solution

Algorithm

Let us consider a hypercube in anisotropic elastic

porous medium Ω = [0, T ] × K{0 ≤ x ≤ 1, 0 ≤ y ≤

1, 0 ≤ z ≤ 1}. Let equation (1) describe the ﬂuid dy-

namics in hypercube Ω under initial conditions (2)

and boundary conditions (3).

∂P

∂t

∂

∂x

(φ(x, y, z)

∂P

∂x

) +

∂

∂y

(φ(x, y, z)

∂P

∂y

) +

∂

∂z

(φ(x, y, z)

∂P

∂z

) + f (t, x, y, z) (1)

P(0, x, y, z) = φ(0, x, y, z) (2)

∂P

∂n



= 0 (3)

In equation (1) the solution function P(t, x, y, z)

is the seam pressure in point (x, y, z) at moment t;

φ(x, y, z) is the diffusion coefﬁcient; and f (x, y, z) is

density of sources. To solve the deﬁned problem we

employed Jacobs numerical method and domain de-

composition method from (Malyshkin, 2010).

As a result, we have following solution algorithm:

First, original domain is divided into sub-domains.

Every sub-domain consists of three main parts: ghost

slab, boundary slab and interior slab (see ﬁg. 1).

Data transformations deﬁned by (1)-(3) proceed

independently only in the interior slab. Further com-

putation requires boundary slab values that are stored

DistributedParallelAlgorithmforNumericalSolvingof3DProblemofFluidDynamicsinAnisotropicElasticPorous

MediumUsingMapReduceandMPITechnologies

525

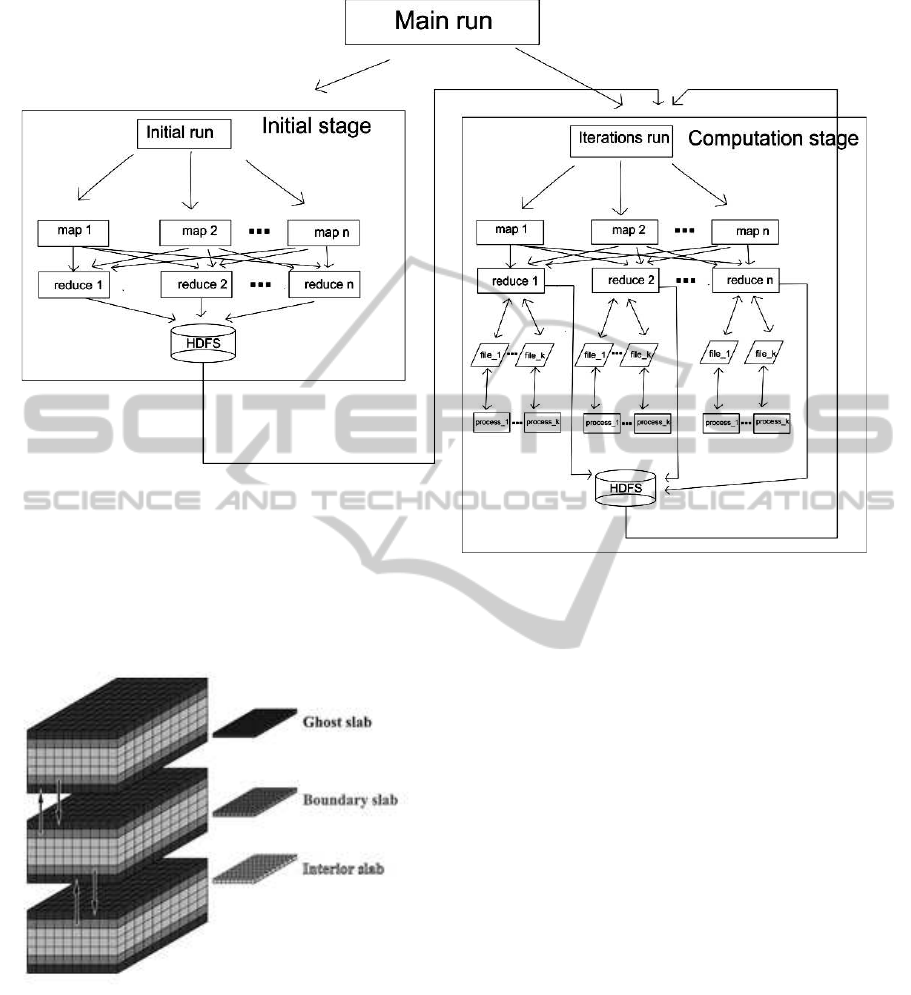
Figure 2: Figure visualizes stages of MapReduce job execution: initialization and computation. At initialization stage mappers

divide data into sub-domains and distribute them between reducer nodes, then reducers compute initial values. Computation

stage makes use of mappers to collect and re-distribute boundary values of each sub-domain at every iteration step. Reducers

restructure the data received from mappers and launch MPI-code to process it.

Figure 1: Figure visulizes how general compuing domain is

divided into several sub-domains to be distributed between

nodes for parallel execution.

in ghost slabs of neighbor sub-domains (i.e.ghost

slabs store copies of neighbors boundary slab values

). As a result, at each iteration sub-domains exchange

their boundary slab values and recalculate their inte-

rior values. The iteration is carried out until user set

termination conditions are met.

3.2 Technological Considerations and

Algorithm Implementation

Review presented in 2 shows that use of MPI technol-

ogy in MapReduce applications can give signiﬁcant

increase in performance. Nonethless, Jacobs algo-

rithm (being used to solve the problem deﬁned in 3.1)

has to be modiﬁed to make the best use of proposed

technological solution. It consists of several stages.

Initialization Stage. First, we call a MapRe-

duce job that computes initial values for a

three-dimensional ﬁeld. The job, ﬁrst, applies

pre-determine method of ﬁeld decomposition (set by

software designer), then assigns every new sub-ﬁeld a

unique key, and passes them to reducer nodes for par-

allel execution. When reducers are ﬁnished they form

an output ﬁle that stores string values in the following

format: (D, R, X

coord

, Y

coord

, Z

coord

). D here is the

datum, R is the reducer id, and X

coord

, Y

coord

, Z

coord

represent coordinates on appropriate axes. It may

be noted that there is no sub-ﬁeld id, this is because

every reducer is assigned its own sub-ﬁeld during

the ﬁrst run and it does not change until the end of

computation.

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

526

Iteration Stage. At this stage, the main iteration

loop of problem solution takes place. Unlike at ini-

tiation step, mapper here is responsible for bound-

ary values exchange between sub-domains. In par-

ticular after each iteration reducers pass mappers

their boundary values for re-distribution while keep-

ing their internal slab in memory. In this way we over-

come network overloading and reduce the ammount

of data transfered.

At the reducer level data obtained from mappers

are written in different ﬁles depending on x coordi-

nates. Then every MPI-process computes its own sub-

set. Depending on the rank an MPI-process treates the

data from the ﬁle entitled out + the rank of the pro-

cess. In other words, data exchange between Hadoop

and MPI involves following steps: data are stored lo-

cally on each of the nodes; then Hadoop reads from

ﬁles in which data are stored, and writes into ﬁles ded-

icated for MPI-processes.

When input data for MPI-processes is distributed,

platform starts the MPI-program itself. In our case it

is developed using MPI-library for Java programming

language. Mainly this decision is driven by the fact

that Hadoop is written in Java and, moreover, it has a

rich set of development and debugging tools.

Unfortunately, it is impossible to directly match

the work of MPI library and Hadoop within one

project medium. As a result, we call the MPI-program

from reducer and it is started as a separated ﬂow.

First, MPI-program reads the data from the assigned

ﬁle and then writes them in a three-dimensional ﬁle

which will be needed to scale the values in the points

form the subﬁeld assigned for this process. The val-

ues in a three-dimensional ﬁle are converted accord-

ing to the algorithm, and the new converted values are

written in the corresponding ﬁle for the given MPI-

process for the possibility of the their further process-

ing on the side of reducer.

If the rank of the process is equal to 0 or the num-

ber of process -1, the top layer and the bottom ad-

ditional layer which were distributed for processing

remain unchanged. After this, the process of com-

puting is transferred again to Reducer. Then, at stage

Reduce, the data on all points computed, at stage MPI

are grouped so that statical data are written (recorded)

into local ﬁle system of the given node on which

Reducer is fulﬁlled, and the boundary values sub-

jected to exchange are reduced for further distribution

of these values for the rest nodes which need these

boundary values. Both stages of execution are vizual-

ized in ﬁg. 2.

4 CONCLUSIONS

In conclusion, main novelty of the designed solution

is the organization of its iterative scheme with the el-

ements of MPI programming. However, presented re-

sults lack testing data and, as a result, may raise ques-

tions that can not be answered at this stage. Thus,

further actions primarily include testing the platform

prototype implementation and adjusting further action

in accordance with the actual results.

ACKNOWLEDGEMENTS

Research is funded under Kazakhstan government

scientiﬁc grant “Developing models and applications

of MapReduce-Hadoop based high-performance dis-

tributed data processing for oil extraction problems”.

REFERENCES

Becker, J. C. and Dagum, L. (1992). Particle simulation on

heterogeneous distributed supercomputers. In HPDC,

pages 133–140.

Biardzki, C. and Ludwig, T. (2009). Analyzing metadata

performance in distributed ﬁle systems. In Malyshkin,

V., editor, Parallel Computing Technologies (10th

PaCT’09), volume 5698 of Lecture Notes in Computer

Science (LNCS), pages 8–18. Springer-Verlag (New

York), Novosibirsk, Russia.

Bu, Y., Howe, B., Balazinska, M., and Ernst, M. D. (2012).

The haloop approach to large-scale iterative data anal-

ysis. VLDB J, 21(2):169–190.

Cappello, F., Djilali, S., Fedak, G., H

erault, T., Magniette,

F., N

eri, V., and Lodygensky, O. (2005). Computing

on large-scale distributed systems: Xtremweb archi-

tecture, programming models, security, tests and con-

vergence with grid. Future Generation Comp. Syst,

21(3):417–437.

Chen, S. S., Dongarra, J. J., and Hsiung, C. C. (1984). Mul-

tiprocessing linear algebra algorithms on the Cray X-

MP-2: Experiences with small granularity. Journal of

Parallel and Distributed Computing, 1(1):22–31.

Cohen, J. (2009). Graph twiddling in a mapreduce world.

Computing in Science and Engineering, 11(4):29–41.

Dean, J. and Ghemawat, S. (2008). MapReduce: simpliﬁed

data processing on large clusters. CACM, 51(1):107–

113.

ıaz, J., Mu

noz-Caro, C., and Ni

no, A. (2012). A survey

of parallel programming models and tools in the multi

and many-core era. IEEE Trans. Parallel Distrib. Syst,

23(8):1369–1386.

Ekanayake, J., Li, H., Zhang, B., Gunarathne, T., Bae, S.-

H., Qiu, J., and Fox, G. (2010). Twister: a runtime

for iterative mapreduce. In Hariri, S. and Keahey, K.,

editors, HPDC, pages 810–818. ACM.

DistributedParallelAlgorithmforNumericalSolvingof3DProblemofFluidDynamicsinAnisotropicElasticPorous

MediumUsingMapReduceandMPITechnologies

527

Fagg, G. E. and Dongarra, J. (2000). FT-MPI: Fault tolerant

MPI, supporting dynamic applications in a dynamic

world. In Dongarra, J., Kacsuk, P., and Podhorszki,

N., editors, PVM/MPI, volume 1908 of Lecture Notes

in Computer Science, pages 346–353. Springer.

Foug

ere, D., Gorodnichev, M., Malyshkin, N., Malyshkin,

V. E., Merkulov, A. I., and Roux, B. (2005). Numgrid

middleware: MPI support for computational grids.

In Malyshkin, V. E., editor, PaCT, volume 3606 of

Lecture Notes in Computer Science, pages 313–320.

Springer.

Gropp, W., Lusk, E. L., Doss, N. E., and Skjellum, A.

(1996). A high-performance, portable implementa-

tion of the MPI message passing interface standard.

Parallel Computing, 22(6):789–828.

Jin, H. and Sun, X.-H. (2013). Performance comparison un-

der failures of MPI and mapreduce: An analytical ap-

proach. Future Generation Comp. Syst, 29(7):1808–

1815.

Liu, H. and Orban, D. (2008). Gridbatch: Cloud computing

for large-scale data-intensive batch applications. In

CCGRID, pages 295–305. IEEE Computer Society.

Lu, X., Wang, B., Zha, L., and Xu, Z. (2011). Can MPI ben-

eﬁt hadoop and mapreduce applications? In Sheu, J.-

P. and Wang, C.-L., editors, ICCP Workshops, pages

371–379. IEEE.

Malyshkin, V. (2010). Assembling of Parallel Programs

for Large Scale Numerical Modelling. IGI Global,

Chicago, USA.

Matsunaga, A. M., Tsugawa, M. O., and Fortes, J. A. B.

(2008). CloudBLAST: Combining mapreduce and

virtualization on distributed resources for bioinfor-

matics applications. In eScience, pages 222–229.

IEEE Computer Society.

Mohamed, H. and Marchand-Maillet, S. (2012). Enhancing

mapreduce using MPI and an optimized data exchange

policy. In ICPP Workshops, pages 11–18. IEEE Com-

puter Society.

Ng, R. T. and Han, J. (1994). Efﬁcient and effective cluster-

ing methods for spatial data mining. Technical Report

TR-94-13, Department of Computer Science, Univer-

sity of British Columbia. Tue, 22 Jul 1997 22:21:44

GMT.

Pandey, S. and Buyya, R. (2012). Scheduling workﬂow

applications based on multi-source parallel data re-

trieval in distributed computing networks. Comput.

J, 55(11):1288–1308.

Slawinski, J. and Sunderam, V. S. (2012). Adapting MPI

to mapreduce paaS clouds: An experiment in cross-

paradigm execution. In UCC, pages 199–203. IEEE.

Srirama, S. N., Batrashev, O., Jakovits, P., and Vainikko, E.

(2011). Scalability of parallel scientiﬁc applications

on the cloud. Scientiﬁc Programming, 19(2-3):91–

105.

Sunderam, V. S., Geist, G., and Dongarra, J. (1994). The

PVM concurrent computing system: evolution, expe-

riences, and trends. Parallel Computing, 20(4):531–

545.

Valilai, O. and Houshmand, M. (2013). A collaborative and

integrated platform to support distributed manufactur-

ing system using a service-oriented approach based on

cloud computing paradigm. Robotics and computer-

integrated manufacturing, 1(29):110–127.

Wang, J. and Liu, Z. (2008). Parallel data mining optimal

algorithm of virtual cluster. In Ma, J., Yin, Y., Yu,

J., and Zhou, S., editors, FSKD (5), pages 358–362.

IEEE Computer Society.

ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications

528