
Preservation of Non-uniform Memory Architecture Characteristics when
Going from a Nested OpenMP to a Hybrid MPI/OpenMP Approach
M. Ali Rostami and H. Martin B
¨
ucker
Institute of Mathematics and Computer Science, Friedrich-Schiller-University Jena, Ernst-Abbe-Platz 2, Jena, Germany
Keywords:
Parallel Programming, Shared Memory, Distributed Memory, Hybrid Parallel Programming, SHEMAT-suite.
Abstract:
While the noticeable shift from serial to parallel programming in simulation technologies progresses, it is
increasingly important to better understand the interplay of different parallel programming paradigms. We
discuss some corresponding issues in the context of transforming a shared-memory parallel program that
involves two nested levels of parallelism into a hybrid parallel program. Here, hybrid programming refers to
a combination of shared and distributed memory. In particular, we focus on performance aspects arising from
shared-memory parallel programming where the time to access a memory location varies with the threads.
Rather than analyzing these issues in general, the focus of this position paper is on a particular case study from
geothermal reservoir engineering.
1 INTRODUCTION
With the ongoing transition from serial to parallel
computing the field of simulation and modeling is
increasingly faced with the challenge of using, de-
veloping, and maintaining parallel software. Under
certain circumstances, it can take significant effort to
move from serial to parallel processing. Moreover,
parallel computing turns out to be extremely difficult
if a high performance is required on a large number
of processes. Parallelism also brings variety to pro-
gramming. There are different parallel programming
paradigms with strengths and weaknesses. The choice
of the programming paradigm significantly influences
the effort needed to develop a parallel software.
Today, the two most prominent parallel program-
ming paradigms are message passing for distributed-
memory computers and user-directed parallelization
for shared-memory computers. For distributed and
shared memory, the most widely used paradigms are
the message passing interface (MPI) (Snir et al., 1998;
Gropp et al., 1998) and OpenMP (Chapman et al.,
2008; OpenMP Architecture Review Board, 2013),
respectively. When increasing the number of paral-
lel processes, it is reasonable to combine these two
paradigms in a hybrid MPI/OpenMP approach (Jost
and Robins, 2010; Wu and Taylor, 2013). While
this combination is straightforward to implement for
experienced parallel programming experts, it proved
difficult to achieve a performance that is somewhere
near the peak performance. There are some subtle is-
sues that can effect the performance dramatically.
It is not our aim to provide a general discussion
on hybrid parallel programming. We rather focus on
a specific situation at hand which involves a two-level
nested OpenMP parallelism. That is, a new team of
threads is spawned from within each thread of a team
of threads. This nested OpenMP parallelism is specif-
ically tuned for a shared-memory system with a non-
uniform memory architecture (NUMA). In such a sys-
tem, the time to access a location of a shared mem-
ory depends on the “distance” of that location to the
processor. So, the memory access time varies with
the threads. For performance reasons, it is crucial to
find a layout of the data structures in memory such
that threads mostly access those memory locations
that can be accessed quickly. Typically, it requires
considerable human effort to find such a “NUMA-
aware” memory layout. When going from a nested
OpenMP approach to a hybrid MPI/OpenMP ap-
proach, it is therefore important to ensure the preser-
vation of NUMA-awareness.
The aim of this position paper is to demonstrate
these issues for a particular real-world application
from geothermal engineering. It is interesting to men-
tion that, in the general field of geosciences, the cur-
rent trend is to move from a serial to a parallel soft-
ware; see (O’Donncha et al., 2014) and the references
therein. So, our discussion of preserving NUMA-
awareness in a hybrid MPI/OpenMP software goes
beyond the current state-of-the art. In Sect. 2, we
sketch the specific software that is used as a case
286
Rostami M. and Bücker H..
Preservation of Non-uniform Memory Architecture Characteristics when Going from a Nested OpenMP to a Hybrid MPI/OpenMP Approach.
DOI: 10.5220/0005110902860291
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),
pages 286-291
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

study throughout this article. We then demonstrate
in Sect. 3 how this serial software is converted into a
NUMA-aware parallel software. Finally, we describe
an approach to transform this shared-memory paral-
lel program into a hybrid MPI/OpenMP program in
Sect. 4 and draw some conclusions in Sect. 5.
2 RESERVOIR ENGINEERING
In this section we summarize the main functional-
ity of a software package for the solution of prob-
lems in geothermal reservoir engineering. This soft-
ware package is called Simulator for Heat and Mass
Transport (SHEMAT-Suite) (Bartels et al., 2003; Rath
et al., 2006). It solves the coupled system of par-
tial differential equations governing fluid flow, heat
transfer, species transport, and chemical water-rock
interactions in fluid-saturated porous media. Follow-
ing the notation in (Wolf, 2011), Table 1 compiles a
list of relevant physical quantities and symbols. Using
these quantities, SHEMAT-Suite solves the equation
describing ground water flow
∇ ·
ρ
f
g
µ
f
k · ∇h
+ Q = S
∂h
∂t
for the hydraulic head h as well as the equation repre-
senting heat transport
∇ ·
λ
e
∇T
− (ρc)
f
v · ∇T + A = (ρc)
e
∂T
∂t
for the temperature T . For the sake of simplicity, we
omit the formulation of suitable boundary conditions.
These two equations are coupled via the Darcy veloc-
ity defined by
v =
ρ
f
g
µ
f
k · ∇h.
The flow and transport equations are numerically
solved using a block centered finite difference scheme
on a Cartesian grid in two or three spatial dimensions.
Solving the above equations for hydraulic head
and temperature is referred to as the forward problem.
In addition to solving forward problems, SHEMAT-
Suite is also capable of solving inverse problems. Ac-
cording to (Tarantola, 2004), inverse problems consist
of using some measurements to infer the values of pa-
rameters that characterize the system of interest. They
try to determine the model parameters from experi-
mental data, which are generated randomly or mea-
sured from the actual environment. In other words, an
inverse problem is a general framework used to con-
vert observed measurements into information about a
physical object or system. Inverse problems arise not
Table 1: List of physical quantities that are relevant to the
SHEMAT-Suite.
Symbol Meaning Unit
h hydraulic head [m]
Q source term [m
3
s
−1
]
k hydraulic permeability [m
2
]
ρ
f
density [kgm
−3
]
g gravity [ms
−2
]
µ
f
dynamic viscosity [Pas]
t time [s]
S storage coefficient [m
−1
]
T temperature [
◦
C]
A conductive term [W m
−3
]
of heat production
(ρc)
e
heat capacity [Jm
−3
K
−1
]
λ
e
thermal conductivity [W m
−1
K
−1
]
(ρc)
f
thermal capacity [Jkg
−1
K
−1
]
v Darcy velocity [ms
−1
]
only in reservoir engineering, but also in many differ-
ent areas including mathematical finance, astronomy,
image processing, and material science.
Monte Carlo (MC) methods are an important class
for the solution of inverse problems. These stochas-
tic techniques use random sampling and probability
statistics to solve various types of problems. Any
method that solves a problem by generating suitable
random values for the input and then examines the
distribution of the resulting output is called an MC
method. A number of random configurations are used
to sample a complex system and this system is ex-
plained by the results obtained from the solution of
multiple forward problems. There is a variety of dif-
ferent MC methods. The general outline of such a
method is as follows:
1. Define a domain on which the input is based.
2. Generate input data from a probability distribution
over this domain.
3. Solve a forward problem several times using dif-
ferent input data. A single solution of a forward
model is called realization.
4. Compute some average which is a summary over
all previous results of the realizations.
The independence of any two realizations and the
high computational complexity of an MC method
suggest to reduce the time for the solution of an in-
verse problem by computing multiple realizations in
parallel. This is discussed in the next section.
PreservationofNon-uniformMemoryArchitectureCharacteristicswhenGoingfromaNestedOpenMPtoaHybrid
MPI/OpenMPApproach
287
3 NUMA-AWARENESS
To reduce the time for the solution of a forward prob-
lem, SHEMAT-Suite is parallelized using OpenMP,
the de facto standard for parallel programming of
shared-memory systems. In addition, there is an
OpenMP parallelization of an MC method. Through-
out this position paper, we do not focus on comput-
ing the forward model in parallel, but on the paral-
lelization of the MC method. The current implemen-
tation involves a nested OpenMP parallelization, i.e.,
two levels of parallelism on top of each other. The
outer parallelization consists of computing different
realizations in parallel, whereas the inner level is con-
cerned with parallelizing the forward problem. For
instance, the inner level includes the parallel solution
of a system of linear equations as well as the parallel
assembly of the corresponding coefficient matrix.
In the MC method, the program computes the
solution of the forward problem several times. Here,
these realizations are independent of each other.
However, the input and output needs to be handled
carefully. The realizations are computed in parallel
by a team of OpenMP threads. To illustrate the strat-
egy behind the OpenMP implementation, consider a
five-dimensional array declared as, say,
x(n x,n y,n z,n k,n j) (1)
in the serial code. Think of some physical quantity
x discretized on a three-dimensional spatial grid of
size n
x
× n
y
× n
z
with two additional dimensions
representing n
k
and n
j
discrete values for two further
characteristics. In the OpenMP implementation, all
major arrays are extended by another dimension that
represents the realizations. That is, in the OpenMP-
parallelized code, the array (1) is transformed into
the data structure
x(r,n x,n y,n z,n k,n j) (2)
whose first dimension allocates additional storage for
the computation of r realizations. This paralleliza-
tion strategy increases the storage requirement by a
factor of r as compared to the serial software. How-
ever, it is shown in (Wolf, 2011) that this strategy is
advantageous for bringing together parallelization of
an MC method for the solution of an inverse prob-
lem with automatic differentiation of the underlying
forward model. The latter is important in the context
of SHEMAT-Suite (Rath et al., 2006), but is not dis-
cussed further in this position paper.
Typically, the number of realizations, r, is much
larger than the number of available OpenMP threads
on the outer level, q. Therefore, each thread will work
on more than one realization. Recall that the realiza-
tions represent independent tasks. The assignment of
the threads to the tasks is carried out using a dynamic
scheduling to balance the computational load among
the threads. That is, each thread will start to work on
the next available task as soon as it finishes its current
task.
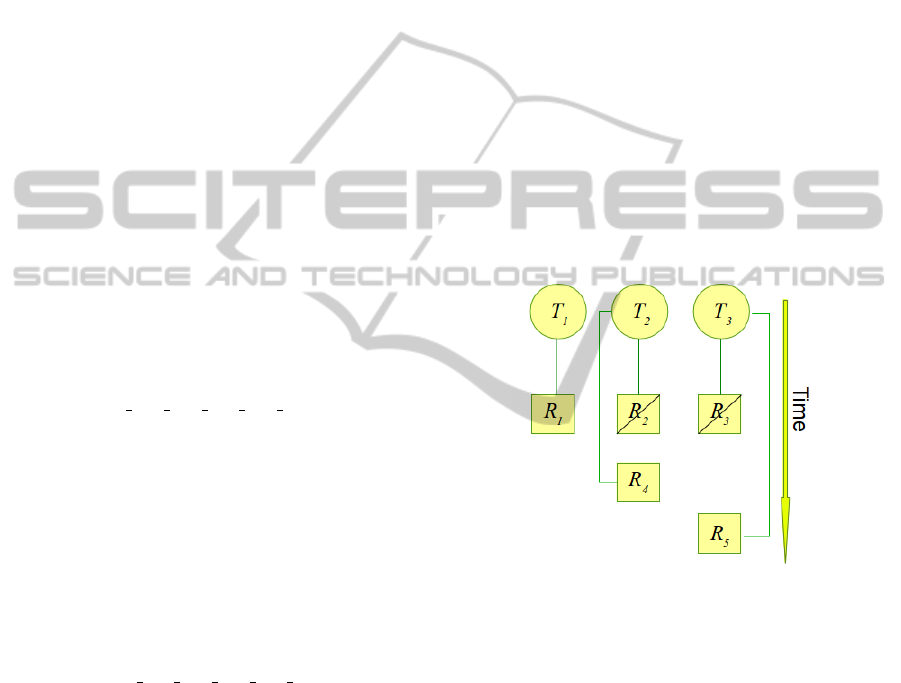
A simple example is illustrated in Figure 1 show-
ing q = 3 OpenMP threads on the outer level which
are handling r = 5 realizations. Initially, these three
threads start to compute the first three realizations.
The realizations will be terminated in any order. Sup-
pose that thread T
2
finishes the computation of the re-
alization R
2
. It then immediately starts to work on the
realization R
4
which is the first realization waiting for
execution. Afterwards, the thread T
3
terminates R
3
and then executes realization R
5
. In that example,
the thread T
1
is still computing the realization R
1
; but
the remaining threads, R
2
and R
3
, are dynamically as-
signed to the realizations that are waiting for execu-
tion.
Figure 1: Dynamic assignment of the realization R
i
to the
OpenMP threads T
i
.
Though this scheduling strategy is simple and ad-
equate, its memory access is irregular. This makes
it difficult to achieve high performance on today’s
shared-memory systems. From a conceptual point
of view, there are different classes of shared-memory
systems schematically depicted in Figure 2. In the
first class, processors access the shared memory via
a common bus in a uniform way. This way, all pro-
cesses spend the same time to access different parts of
memory; see the left part of this figure.
A more realistic class is illustrated in the right part
of this figure. Here, the concept of a shared mem-
ory is implemented by putting together multiple lo-
cal memories via an interconnection network. Pro-
cessors access their local memories faster than mem-
ories of other processors. Thus, these shared-memory
systems are referred to as non-uniform memory ac-
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
288

Figure 2: Shared-memory systems with uniform memory
access (left) and non-uniform memory access (right).
cess (NUMA) architectures. In NUMA architectures,
there is a mapping from an address in the global
shared memory to an address in a local memory. In
addition, caches are used to exploit locality of mem-
ory accesses. Within NUMA systems, maintaining
cache coherence across shared memory has a signifi-
cant overhead. Current NUMA systems typically pro-
vide a special hardware to maintain cache coherence
(ccNUMA). The placement of threads to a local mem-
ory is often defined by the first memory access of a
thread. This distribution of data in memory is called
first-touch policy (Bhuyan et al., 2000).
To take full advantage of the NUMA performance
characteristics, SHEMAT-Suite does not follow the
dynamic scheduling strategy illustrated in Figure 1.
In contrast, the modified strategy sketched in Figure 3
is applied. Here, the data from a data structure located
in some address in the shared memory is copied to an
address in the local memory before starting the com-
putation on that data. After the end of the computa-
tion, the data is copied back to the original place. This
way, the parallelization of the MC method is NUMA-
aware, meaning it optimizes memory accesses as fol-
lows.
Figure 3: Dynamic assignment of the realization to the
OpenMP threads taking advantage of a NUMA system.
The OpenMP implementation is designed such
that the local memory for each thread remains fixed
after having executed the first realization on each
thread. Suppose there are r realizations and q threads
on the outer level with r > q. At first, the program
computes the first r realizations in parallel. Since the
first-touch policy is applied, this execution allocates
the slices of the major arrays corresponding to the
first realizations to the local memory of each thread.
So, the ith slice of an array x(i,...) from (2) is
copied to the memory that is locally accessible from
thread T
i
. Whenever a thread T
j
finishes its current
task, the next realization R
i
with i > q is then sched-
uled for execution on T
j
. When this happens the slices
of all major arrays, x(j,...), are copied to the mem-
ory that is local to T
j
. This process continues until all
realizations are executed.
Finally, the software takes into account this strat-
egy when writing the output to files. The software
uses integer file handlers for accessing files. In the
OpenMP parallelization, some intermediate informa-
tion and the output of each realization is written to a
unique file. Therefore, each thread needs to determine
the file handler of the realization that is currently ex-
ecuted.
4 HYBRID MPI/OPENMP
Current high-performance computing (HPC) systems
are typically made up of clusters of individual com-
puting nodes that are connected via a network. Each
of these nodes can itself consist of a shared-memory
systems. A hybrid MPI/OpenMP parallelization is of-
ten suitable since it allows to exploit the character-
istics of different computer architectures. The idea
behind hybrid parallelization is to take advantage of
the distributed-memory characteristic on the level of
the network that connects nodes and of the shared-
memory characteristic on the level of a computing
node. On the network level, the MPI processes dis-
tribute data and computation over different nodes. On
the node level, the OpenMP threads are used to paral-
lelize computation in the shared memory. It is com-
mon to use these two technologies together.
Figure 4 illustrates the following discussion
schematically. In the top of this figure, a two-level
OpenMP parallelization is sketched. Here, the outer
level is explicitly shown whereas the inner level is im-
plicitly represented by the different realizations that
are individually numbered for each thread of the outer
level. A hybrid MPI/OpenMP parallelization can then
be imagined by the following two strategies. The first
strategy, which is depicted in the middle of this figure,
adds a new level of MPI parallelization on top of the
existing two-level OpenMP approach. The advantage
of this strategy is that it does not need many modifica-
tions in the existing code and it also preserves NUMA
PreservationofNon-uniformMemoryArchitectureCharacteristicswhenGoingfromaNestedOpenMPtoaHybrid
MPI/OpenMPApproach
289
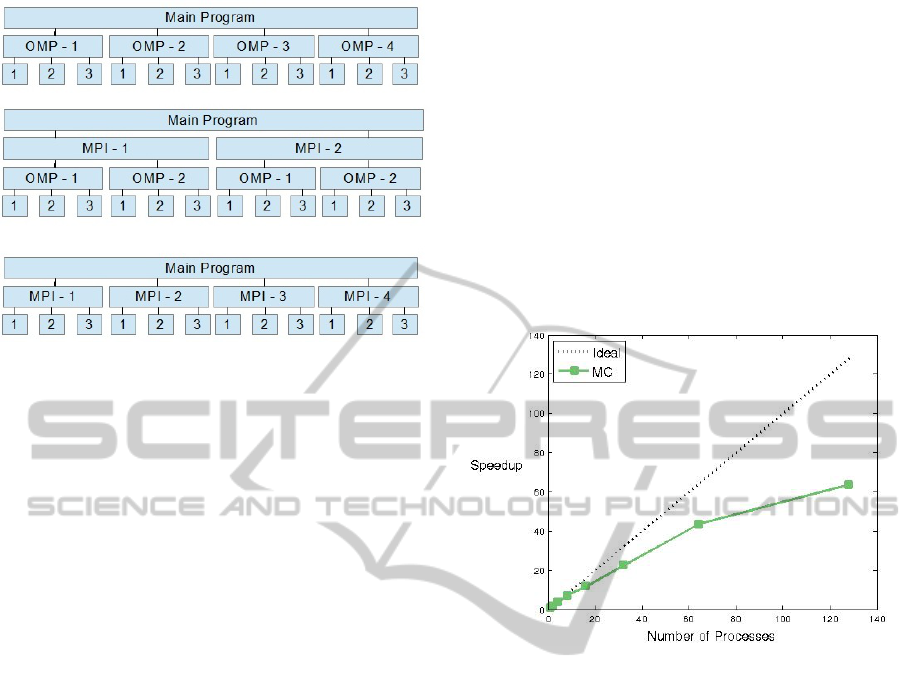
Figure 4: A two-level nested OpenMP parallelization (top),
a hybrid approach based on adding an additional MPI level
on the top of the two OpenMP levels (middle), and a hy-
brid approach where the outer OpenMP level is converted
to MPI (bottom).
characteristics of the outer OpenMP level. The sec-
ond strategy, which is shown in the bottom of this fig-
ure, converts the outer level of OpenMP paralleliza-
tion by an MPI parallelization. Since we want to pre-
serve the NUMA characteristics, we implemented the
first approach. The second approach, though inter-
esting, takes significant more programming effort and
will be considered in the near future.
The first approach has three levels of parallelism
in which the second level is already NUMA-aware.
In this approach, each MPI process contains a two-
level OpenMP parallelization. More precisely, if we
look only at one MPI process, we have a code that is
similar to the existing OpenMP-parallelized program.
Only the indexing of the data structure as well as the
I/O needs to be adapted.
Suppose we are given r realizations, q available
OpenMP threads in the outer level, and p MPI pro-
cesses. These three numbers together with the rank of
an MPI process as well as the index of an OpenMP
thread are used for reindexing that manages the dy-
namic computation of the correct realization on the
correct OpenMP thread and MPI process. The num-
ber of realization per MPI process, r
l
:= r/p, is called
the local number of realizations. Recall that the major
arrays have already been extended by a new dimen-
sion to handle the realizations. In the new implemen-
tation, we reuse this dimension for the local realiza-
tions. If this local number of realization is the same as
the number of available OpenMP threads, each thread
computes a realization. However, NUMA-awareness
becomes important as soon as the r
l
> q. As we leave
this part of the code as before and only change the
indices, this NUMA-awareness is preserved.
We did some preliminary evaluations of this new
implementation. In particular, we compare the MPI
approach and the serial version. For this evalua-
tion, we use an Intel Xeon X5675 Westmere EP with
146.88 GFLOPS and 24 GB memory. The number
of realizations is set to r = 128 and the number of
MPI processes varies from p = 1 to p = 128. We
do not vary the problem size of a realization. Fig-
ure 5 shows the speedup versus the number of MPI
processes. The results indicate that the MPI imple-
mentation scales well for a small number of MPI pro-
cesses. However, the speedup tends to saturate when
increasing the number of MPI processes.
Figure 5: Ratio of the running time of the MPI implemen-
tation and the serial version for r = 128 realizations.
5 CONCLUDING REMARKS
This case study of parallelizing a Monte Carlo method
used in the field of reservoir engineering originates
from the necessity to reduce the overall time to so-
lution for large-scale problems. Here, the goal is to
bring together a nested OpenMP parallelization for
shared memory and an MPI parallelization for dis-
tributed memory. Two different hybrid MPI/OpenMP
parallelization strategies are introduced. The first
strategy is to add a new level of MPI on top of
an existing two-level nested OpenMP parallelization.
The second strategy consists of converting the exist-
ing outer OpenMP level to an MPI parallelization.
We implemented the first strategy as our goal is to
preserve the NUMA characteristics of an existing
OpenMP parallelization.
Although these strategies are discussed in the con-
text of a stochastic approach for the solution of an in-
verse problem, the concept of the first strategy is more
general. Whenever there is an OpenMP parallelized
code, the first strategy can be used to implement a
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
290

hybrid parallelized version of the code without ma-
jor changes. Here, the underlying assumption is that
there is an additional dimension for the paralleliza-
tion added to all major arrays. In this case, the first
strategy is then nothing but a reindexing technique.
ACKNOWLEDGEMENTS
This work is partially supported by the German Fed-
eral Ministry for the Environment, Nature Conser-
vation, Building and Nuclear Safety (BMUB) and
the German Federal Ministry for Economic Affairs
and Energy (BMWi) within the project MeProRisk II,
contract number 0325389 (F) as well as by the Ger-
man Federal Ministry of Education and Research
(BMBF) within the project HYDRODAM, contract
number 01DS13018.
REFERENCES
Bartels, J., K
¨
uhn, M., and Clauser, C. (2003). Numeri-
cal simulation of reactive flow using SHEMAT. In
Clauser, C., editor, Numerical Simulation of Reactive
Flow in Hot Aquifers, pages 5–74. Springer Berlin
Heidelberg.
Bhuyan, L., Iyer, R., Wang, H.-J., and Kumar, A. (2000).
Impact of CC-NUMA memory management policies
on the application performance of multistage switch-
ing networks. IEEE Transactions on Parallel and Dis-
tributed Systems, 11(3):230–246.
Chapman, B., Jost, G., Van der Pas, R., and Kuck, D. J.
(2008). Using OpenMP: Portable shared memory
parallel programming. MIT Press, Cambridge, Mass.,
London.
Gropp, W., Huss-Lederman, S., Lumsdaine, A., Lusk, E. L.,
Nitzberg, B., Saphir, W., and Snir, M. (1998). MPI–
The Complete Reference: Volume 2, The MPI-2 Ex-
tensions. MIT Press, Cambridge, MA, USA.
Jost, G. and Robins, B. (2010). Experiences using hybrid
MPI/OpenMP in the real world: Parallelization of a
3D CFD solver for multi-core node clusters. Scientific
Programming, 18(3–4):127–138.
O’Donncha, F., Ragnoli, E., and Suits, F. (2014). Paral-
lelisation study of a three-dimensional environmental
flow model. Computers & Geosciences, 64:96–103.
OpenMP Architecture Review Board (2013). OpenMP
Application Program Interface, Version 4.0.
http://www.openmp.org.
Rath, V., Wolf, A., and B
¨
ucker, H. M. (2006). Joint
three-dimensional inversion of coupled groundwater
flow and heat transfer based on automatic differen-
tiation: Sensitivity calculation, verification, and syn-
thetic examples. Geophysical Journal International,
167(1):453–466.
Snir, M., Otto, S. W., Huss-Lederman, S., Walker, D. W.,
and Dongarra, J. (1998). MPI–The Complete Refer-
ence: Volume 1, The MPI Core. MIT Press, Cam-
bridge, MA, USA, 2nd edition.
Tarantola, A. (2004). Inverse Problem Theory and Meth-
ods for Model Parameter Estimation. Society for In-
dustrial and Applied Mathematics, Philadelphia, PA,
USA.
Wolf, A. (2011). Ein Softwarekonzept zur hierarchischen
Parallelisierung von stochastischen und determinis-
tischen Inversionsproblemen auf modernen ccNUMA-
Plattformen unter Nutzung automatischer Programm-
transformation. Dissertation, Department of Com-
puter Science, RWTH Aachen University.
Wu, X. and Taylor, V. (2013). Performance modeling of
hybrid MPI/OpenMP scientific applications on large-
scale multicore supercomputers. Journal of Computer
and System Sciences, 79(8):1256–1268.
PreservationofNon-uniformMemoryArchitectureCharacteristicswhenGoingfromaNestedOpenMPtoaHybrid
MPI/OpenMPApproach
291
