Identifying Semantic Classes within Student’s Data Using Clustering

Technique

Marek Jaszuk, Teresa Mroczek and Barbara Fryc

Faculty of Information Technology, University of Information Technology and Management,

Sucharskiego 2, Rzesz

ow, Poland

Keywords:

Semantic Class, Automatic Ontology Building, Clustering Methods.

Abstract:

The paper discusses the problem of discovering semantic classes which are the basic building block of any

semantic model. A methods based on clustering techniques is proposed, which leads to discovering related

data coming from survey questions and other sources of information. We explain how the questions can be

interpreted as belonging to the same semantic class. Discovering semantic classes is assumed to be foundation

for construction of the knowledge model (ontology) describing objects being the subjects of the survey. The

ultimate goal of the research is developing a methodology for automatic building of semantic models from

the data. In our case the surveys refer to different socio-economic factors describing student’s situation. Thus

the particular goal of the work is construction of the knowledge model, which would allow for predicting the

possible outcomes of the educational process. The research is, however, more general, and its results could

be used for analyzing collections of objects, for which we have data coming from surveys, and possibly some

additional sources of information.

1 INTRODUCTION

Knowledge management (KM) is an important topic

in many areas of applications, such as artiﬁcial in-

telligence, medicine, natural language processing,

e-commerce, bio-informatics, education, intelligent

information integration, and others (A. Gmez-Prez,

2007; N. F. Noy, 2001). Majority of KM technolo-

gies use some kind of ontology for representing a set

of concepts and relationships between them for a spe-

cialized domain or ﬁeld of interest. Such an ontology

models the domain and represents structural and con-

ceptual information about it.

Building an ontology is a complex and demand-

ing work. The most common approach is based on

hiring a domain expert in cooperation with an ontol-

ogy engineer. The work of the expert is to identify

all the concepts important for the domain of interest

and their mutual relationships. This task is performed

manually and partially supported by an ontology edit-

ing software. The automation of this process is highly

desired and is a huge challenge for the information

science.

A number of techniques based on some kind

of data mining algorithms is being developed

(G. S. Davidson, 2010; Gorskis and Chizhof, 2012).

Their purpose is either to completely automatize the

ontology building process, given some set of sample

data, or at least partially support the process, by con-

structing an initial skeleton of the ontology. In the

second case the key decisions are still left to the do-

main expert.

A typical pipeline of automatized ontology build-

ing approach starts from gathering some raw data de-

scribing inherently the given domain. The purpose of

applying the data mining techniques is identifying the

concepts and their relationships. This leads to discov-

ering the domain model. Given appropriate interpre-

tation, the results obtained with data mining can then

be transformed into a formal ontology model.

The paper introduces a method of automatic ontol-

ogy building for data coming from different sources.

In particular the data are gathered from surveys con-

ducted on university students, and grammar school

students. We want to build semantic model in order to

be able to construct a diagnostic system, which would

deliver valuable information to the school or univer-

sity authorities. The model is necessary for identify-

ing information with the same meaning, and integrat-

ing data coming from different sources, e.g. different

surveys, which were formulated differently using nat-

ural language expressions. We want to overcome the

371

Jaszuk M., Mroczek T. and Fryc B..

Identifying Semantic Classes within Student’s Data Using Clustering Technique.

DOI: 10.5220/0005111403710376

In Proceedings of 3rd International Conference on Data Management Technologies and Applications (DATA-2014), pages 371-376

ISBN: 978-989-758-035-2

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

variety of the ways of expressing different natural lan-

guage questions in surveys.

The paper is organized as follows: In Sec. 2 we

discuss the input data that we collect for the system.

Sec. 3 describes the structure of the whole system,

and the idea of semantic distance and identiﬁcation of

meaning, which can be applied to survey questions.

In Sec. 4 the initial experimental results are demon-

strated and discussed.

2 THE INPUT DATA

In our case the domain of interest is knowledge about

university and secondary school students. The task

is constructing a model representing all the factors

of socio-economic situation of students in relation to

their educational success. Such a model is very de-

sirable for educational institution authorities. If con-

structed properly, it can deliver valuable information

about the possible risks or opportunities in the edu-

cational process. This refers both to the group of stu-

dents treated as a whole, as well as individuals in each

of the groups.

The source of data about the students are surveys,

with questions referring to things such as their attitude

to study, motivations, plans, economic situation, and

other factors, which could be potentially important

for assessing their chance for the educational success,

or possible risks leading to failure. The survey data

are combined with some additional information from

the school computer system, such as sex, the year of

study, the grades.

The detailed information about the students

should be transformed into a knowledge model,

which would allow for making precise diagnoses on

new groups of students. The problem, however, is the

right choice of the survey questions. There is a huge

variety of the possible questions, that could be asked.

On the other hand the survey cannot be too long, to

not make it annoying. Thus we need to select the

questions, which will bring as much information to

the system as possible. The optimal selection can be

found only experimentally, as a result of an iterative

process. We do this by choosing some initial selection

of questions, and observing how the students answer

the them, and how do the results correlate with their

study results. After several iterations, we should get a

survey of satisfactory quality.

This process has, however, some drawbacks. Even

if we ﬁnd some choice of questions, this does not

mean, that we do not want to change it in the future.

The need for change can result from many different

reasons, like changes in political and economic situ-

ation in the country, changes in law referring to ed-

ucation, or changes in the groups of students, espe-

cially in case of internationally open educational in-

stitution, which collects students from all around the

world. On the other hand we would like to integrate

the knowledge acquired after modiﬁcations of the sur-

veys, with the knowledge before modiﬁcations. Oth-

erwise we would lose a huge amount of statistically

relevant data. This is not an easy task, because it re-

quires identiﬁcation of meanings standing behind par-

ticular survey questions, and matching different ver-

sions of the surveys. The knowledge engineering ap-

proach recommends in such situations constructing an

ontology, which would allow for matching different

versions of surveys.

Constructing an ontology is, however, a demand-

ing task. An ontology is a formalized structure of

concepts and their mutual relations. The initial point

in ontology building is precisely deﬁning the set of

concepts and the possible relationships (semantic vo-

cabulary). This is difﬁcult, even if the concepts are

represented with single words or simple phrases. In

case of surveys, the questions are formulated in the

form of sentences, and our task is to identify the pre-

cise meaning of the question (semantic concept). Ev-

ery sentence is a complex expression in natural lan-

guage, and its meaning changes even if we change a

single word in the sentence. This obviously will lead

to different answers of the questioned persons. On

the other hand, the same question could be asked in

several different ways, i.e. we would have something

that can be considered synonymy among the ques-

tions. This makes manual building of the ontology for

the considered problem even more difﬁcult. Thus we

propose another approach, which tries to determine

the meanings in an automatic way, and in this way de-

termine the ontology nodes (semantic classes). Each

question will be matched to one of the nodes.

3 IDENTIFICATION OF

MEANING

3.1 The Structure of the System

We treat the surveys as a natural language interface to

the system. The questions in the interface may vary,

and refer to different areas of interest, however, the

structure of meanings (ontology) that stands behind

the questions, is something relatively unchangeable.

To discover the mapping between the interface, and

the meanings, we need to have some reference data.

Our methodology is based on the assumption of a spe-

DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications

372

ciﬁc application of the designed system. We do not

want to discover a general purpose ontology, but on-

tology of concepts relevant for some speciﬁc purpose.

The goal is in this case assessing the chance for edu-

cational success or failure. There are several factors,

which can be used as indicators of results of educa-

tion. The most obvious are the grades of the ques-

tioned persons. The other factor refers to outstanding

achievements, e.g. in the ﬁeld of scientiﬁc activity.

Yet another one, which indicates educational failure

is information about resigning from the study. In our

university, all persons resigning from the study are

asked for ﬁlling a short questionnaire, in which they

indicate the reason for breaking the study. This brings

additional information to the system, and allows for

constructing a more precise model.

The consequence of the above assumptions is a

system composed of three main elements: the natural

language interface (the surveys), the meanings (nodes

of the ontology related to the particular application),

the indicators of the educational success (Fig. 1). The

surveys are prepared by the experts in the ﬁeld, i.e.

sociologists, psychologists, or educators. The refer-

ence data comes from the school databases.

Natural

language

interface

Output data

Semantic model

Clusteriz

ation

Mapping

Deci

on suppo

Figure 1: The structure of the considered system.

In our approach, the interface is vague and un-

known element, the output data is something that we

know about the subjects of experiments, and the se-

mantic model is something that results from analyz-

ing the survey data in relation to the output data. The

purpose of the work is to build a system, which de-

livered data from the survey, transforms them into the

semantic model. The semantic model in combination

with some machine learning apparatus should gener-

ate predictions about the most likely result of edu-

cation. The prediction can refer both to the grades

(possibly indicating a group of subjects, in which the

student will perform better or worse), or to achieving

outstanding results, or to the chance of breaking the

study because of some speciﬁc reason.

3.2 The Output Data

The output data is assumed to be something that we

know about the students, and what refers to educa-

tional success. For example considering the infor-

mation about the grades, we have to classify the stu-

dents into one of possible groups. The simplest ap-

proach would be computing the grade average, and

divide the average into a number of categories. In this

way a student would fall into one of the categories,

which would determine the class of his educational

success. Computing the average can be, however, too

simplistic. Some students are predisposed into one

group of subjects, while the others are predisposed

into another. Thus we are considering a more general

approach, in which we cluster the objects (students)

within the space spanned by the grades from partic-

ular subjects. In this way we determine the class of

educational success for each student, by classifying

him as belonging to one of the clusters.

3.3 Semantic Distance

Now we should explain the key point of the method.

As already mentioned, we do not know the concepts

a priori. In fact the number of possible concepts is

very large, due to huge variety of possible linguistic

expressions in survey questions. Constructing a pre-

cise semantic model reﬂecting all the possible mean-

ings of the questions is useless, because it would lead

to a very ﬁne-grained and computationally inefﬁcient

model. We prefer to have a rougher model, made of

more coarse grained concepts. To identify the model

we use a clustering technique.

The starting point to identify the concepts is

deﬁning the semantic distance between particular

survey questions. To explain the method for ﬁnding

the semantic distance, let us have a closer look at

the training data. The data for building the model

come from the students, who ﬁlled the survey, and we

have the output information about their educational

success. To be more precise, the success information

is deﬁned as a number of categories. In the simplest

approach, every student is classiﬁed as belonging

into one of the categories. In general he can belong

to more than just one category, but to explain the

idea we will limit the considerations to the single

category. Let us assume, that N is the number of

success categories. Every student, except the success

category, is assigned some input vector resulting

mainly form the answers to the questions, and pos-

sibly from some additional information that we have

about the student. The input is deﬁned as a binary

vector. Even if the original formulation of questions

seen by the students is different, every survey can be

transformed into a binary vector. As a result, every

student can be considered an object characterized by

the following vector in M-dimensional space:

IdentifyingSemanticClasseswithinStudent'sDataUsingClusteringTechnique

373

= {I

: k ∈ 1, . . . M}, (1)

where O

is the i-th object, I

is the k-th coordinate of

the input vector, and we will call it a ”feature”. M is

the number of features.

Obviously a single feature can appear in objects

belonging to different success categories. After col-

lecting data for a group of students, we get some dis-

tribution of the features in respect to the success cate-

gories into which they have been classiﬁed. In conse-

quence, every feature has some deﬁned probability of

belonging to each of the categories:

= (P

, P

, . . . , P

), (2)

where P

is the probability, that a feature numbered

k (I

) was found in the success category numbered n.

We could write this as P(I

|n).

The probabilities vector (2) is the factor deﬁning

the meaning of every feature in our approach. To be

more precise, important is not the vector itself, but

its direction. Thus the distance between two features

in semantic space is measured as the angle between

respective vectors, or more conveniently as a cosine

of the angle between the vectors. The cosine is the

semantic similarity measure, which is the basis for

further computations. In this way the features with

identical meaning have the maximal similarity equal

to 1, and the features with completely different mean-

ing have the similarity equal to 0. The similarity S

between two features P

and P

we will calculate in

a standard way as:

= cosα

· P



, (3)

We have to explain the motivation for making such

an assumption. If some feature is expressed using nat-

ural language, then there is a chance, that there will

be another feature, which will expressed in a differ-

ent form, but will have the same meaning. This has

already been mentioned as synonymy. Usually, in a

carefully designed survey, we will not ﬁnd the same

question twice. Our considerations, however, have a

more general nature. We treat the survey only as a par-

ticular example of a more general class of methods,

where collecting information is performed through a

set of unformalized natural language expressions. A

good example of such methods are medical tests, like

physical examination, where the symptoms are de-

scribed using sentences in natural language. In a set

of such descriptions, a large number of synonymic ex-

pressions can be found. Even in case of surveys, when

the survey is repeated, it can be modiﬁed many times.

The purpose is to optimize the survey to make it max-

imally friendly, and understandable for the individu-

als being examined, as well as to maximize the intake

of valuable information. Formulating a good survey

is not easy, because it requires experimental veriﬁca-

tion, and examination of the people’s answers to the

questions. Sometimes it is necessary to make several

attempts, before the optimal choice of questions can

be found. But the questions still can be modiﬁed, es-

pecially on a larger time scale. After collecting dif-

ferent versions of the modiﬁed survey, there is a large

chance to ﬁnd many questions with the same or close

meaning, but formulated differently.

In many cases we want to integrate the different

versions of the surveys in order to integrate the col-

lected data. This is especially useful, when we want

to use unique historical data, which cannot be recre-

ated. To make possible integration of different sur-

veys, one should create a mapping between the dif-

ferent surveys. For two surveys, this could be a di-

rect mapping, but for larger number of surveys, it is

much more convenient, to build a single ontology,

which will integrate all the surveys. Building such

an ontology in a standard approach would require a

lot of manual work. In our approach, such mapping

will be performed automatically, by creating the se-

mantic model of the questions/features, and mapping

between the features and the model, no matter what

version of the survey do we have. There is only one

requirement, to make this comparison possible. The

output data (in this case the success categories) have

to be the same for the different surveys. The output

creates some kind of reference to the input data. We

assume, that the input is something that can vary, so

the output needs to remain constant, to be able to cre-

ate the mapping between varying input.

Identifying two features as having the same mean-

ing, does not always imply, that the two features have

the same meaning according to our common sense

understanding. We should remember, that the mean-

ing is deﬁned here in computational terms. There is

a chance, that two features with completely different

interpretations (according to our understanding), will

have the same meaning according to the presented ap-

proach. This results from the fact that the two features

are associated with the same educational success clas-

siﬁcation. In consequence, in terms of computational

meaning they should be treated as synonyms.

Actually the exact synonymy is rather theoretical

concept, because it is very unlikely, that we ﬁnd two

features, with semantic similarity equal to 1. To be

more realistic we have to assume, that even if the sim-

ilarity between two features is not 1, they can still be

treated as synonyms if their similarity is close to 1.

Thus to ﬁnd synonyms, we have to ﬁnd the groups

of very similar features. This task can be achieved

by clustering in the space of meanings. In this way

DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications

374

we can regulate the level of granularity of the resul-

tant model. The larger the clusters, the more coarse

grained the semantic model. This is regulated by the

parameters of the clustering algorithm.

4 THE EXPERIMENTAL

RESULTS

The experiments were carried out on a group of stu-

dents from different specializations at the Univer-

sity of Information Technology and Management in

Rzesz

ow (UITM). We also collected data for students

from the Academic Grammar School associated with

UITM. In particular we took into consideration two

specializations: Information technology and Internal

security. The students from the two groups represent

different motivations, and the approach to study, thus

we selected them to be able to confront the results

for two different groups. The total number of exam-

ined persons from Information technology specializa-

tion was 192. In the Internal security specialization

we examined 70 persons. All the students were the

ﬁrst year students. We chose the ﬁrst year, in order

to be able to repeat the examinations on subsequent

years with the same group but with modiﬁed surveys.

From the grammar school we examined 191 students.

The survey for the university students consisted of 21

questions, but many of them had many suboptions to

choose from, which resulted in several hundreds of

features. For grammar school students, the survey

was shorter, and contained only 14 questions, but this

still results in hundreds of features due to complex

structure of the questions.

The ﬁrst task was determining the output cate-

gories, i.e. the measure of educational success. In

the ﬁrst approach we decided to measure the educa-

tional success solely on the foundation of the grades.

We did clustering within the space of the grades from

particular subjects to determine the groups with dif-

ferent success. We tested different clustering algo-

rithms to compare the results, i.e. Farthest First, Hi-

erarchic, k-Means, X-Means, and Density based clus-

tering. The evaluation of accuracy of particular meth-

ods indicated, that the Farthest First gives the best re-

sults. Thus we used the results generated with this

method for further computations. Of course, the num-

ber of clusters can vary, depending on the clustering

settings. Among the possibilities, we chose 5 clus-

ters as this seemed the best representation of success

groups, but of course also results generated with dif-

ferent number of clusters are worth investigating.

Given the success groups, we can take the second

step, which is clustering of the input features (mainly

coming from the survey questions). This is an ac-

tual test, if the method correctly identiﬁes the closely

related features. The surveys were deliberately con-

structed to contain some groups of related questions.

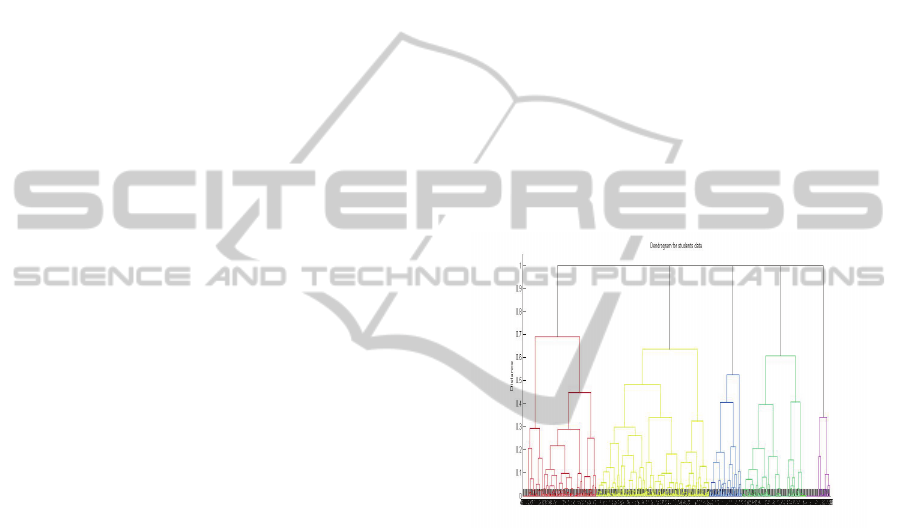
In this step we took the approach based on hierarchic

agglomerative clustering, because this method allows

for easy observation of the changing number of clus-

ters, and cutting off the dendrogram (Fig. 2) to get the

desired number of clusters. While in the ﬁrst cluster-

ing we wanted only to get only several clusters indi-

cating roughly the groups of success, in this case we

are interested in more ﬁne-grained clustering. This

cannot be too ﬁne-grained, because the model would

be to detailed, and difﬁcult to integrate with models

obtained from different surveys. Yet we are interested

in more precise identiﬁcation of meaning. The level

of detail, that we want to achieve, is arbitrary, and the

experiments should indicate, what is the best choice

of granularity of clustering to apply.

Figure 2: The dendrogram of hierarchic clustering of the

input features.

Fig. 3 indicates the number of clusters for the dif-

ferent levels of dendrogram. The maximal number of

clusters is above 500, which is equivalent to the sit-

uation, where each cluster contains a single object.

This is not useful, because the clusters are too small

to identify objects with close meaning. We think, the

sensible number of clusters could be about 100-200.

With such granularity most of the clusters contain sev-

eral closely related features. But of course every-

thing depends on the granularity level that we want

to achieve.

The analysis of contents of particular clusters con-

ﬁrms the validity of the taken approach. Most of them

contain features, which can be interpreted as closely

related. This does not refer to all of them, but as

explained earlier, this does not mean that they can-

not be classiﬁed as synonyms. The most important

thing in the demonstrated approach is the computa-

tional result. Finding the features in the same cluster

IdentifyingSemanticClasseswithinStudent'sDataUsingClusteringTechnique

375

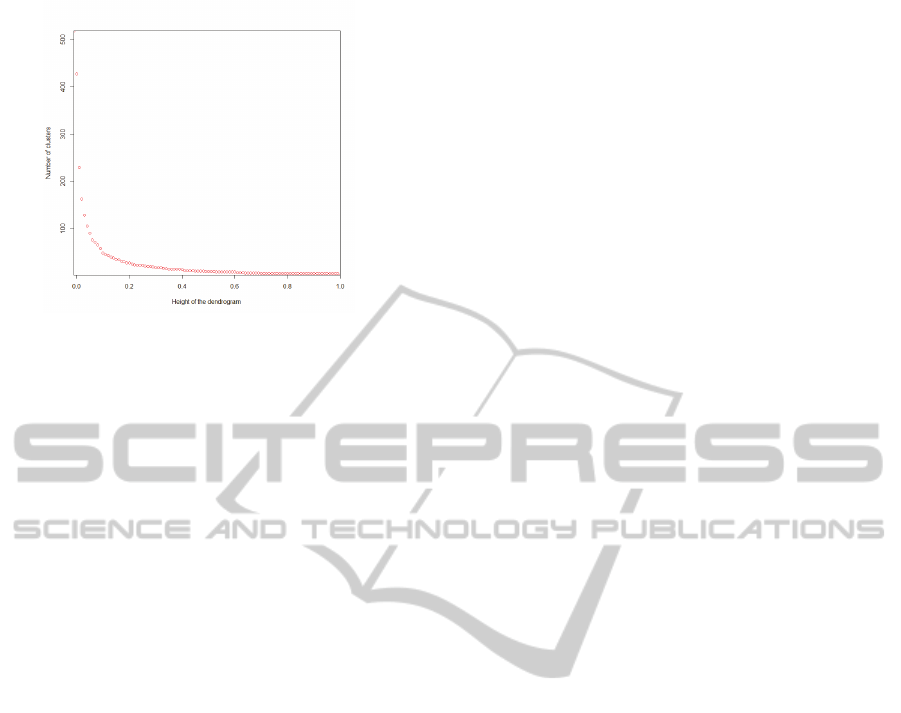
Figure 3: The number of clusters for different cut off level.

means, that they indicate educational success in the

same way. Thus computationally their meaning is the

same.

5 CONCLUSIONS

We demonstrated a method for automatic discovery

of semantic classes standing behind a set of input fea-

tures characterizing a set of factors that allow for as-

sessing the chance for student’s educational success.

The features mainly come from survey questions that

a group of students had to answer. The method is

based on clustering techniques, and the assumption

of the particular purpose of the system, which de-

termines the semantic space. The method is based

on deﬁning the semantic similarity, which allows for

ﬁnding closely related features and their clustering.

The deﬁnition of semantic class is slightly differ-

ent, than in a typical approach, where deﬁning some-

thing as semantic class results from human interpre-

tation. We claim, that when a speciﬁc application is

taken into account, such deﬁnition is better, because it

is associated with the assumed result computationally.

Human designed semantic model is good from the

perspective of human interpretation, but when the re-

sults of computations are taken into account this does

not have to be the best choice. Moreover it is easy

to redeﬁne the semantic model, because its construc-

tion is fully automatic. By redeﬁning the output data

(the success categories in our case) we automatically

redeﬁne the model of input data.

The method was developed using the speciﬁc ap-

plication, but its applicability, as we think, is not lim-

ited to this particular problem. It can be treated as a

more general approach, to solving problems, in which

we have a set of natural language expressions describ-

ing a collection of objects. The natural language in-

terface is something vague and can be formulated in

many different ways, but its purpose is communica-

tion with the investigated persons. The purpose of the

algorithm is to build a model, which would further be

able to perform useful computations.

There is a number of things that are left to be done.

The ﬁrst of them is more thorough analysis of the pos-

sibilities coming from changes in the output data, i.e.

the information about educational success. We also

want to make the quantitative evaluation of the se-

mantic models built on different levels of granular-

ity. Another task is building a machine learning appa-

ratus that would allow for making predictions about

the investigated group of students. Such predictions

could refer both to the group of students as a whole,

as well as indicating individuals needing special treat-

ment, because of the possible chances or threats. Yet

another thing is adding relations between the semantic

classes. The most common element of every ontology

is a hierarchic structure, which associates concepts on

different levels of abstraction with a relation of type

”is subclass of”. We are able to extend the algorithm

to be able to ﬁnd this, and some other kinds of rela-

tions between the classes.

ACKNOWLEDGEMENTS

Project co-ﬁnanced by the European Union from the

European Regional Development Fund and from the

Budget within Regional Operational Programme for

the Podkarpackie Region for the years 2007-2013.

REFERENCES

A. Gmez-Prez, M. Fernndez-Lpez, O. C. (2007). Onto-

logical Engineering: with examples from the areas

of Knowledge Management, e-Commerce and the Se-

mantic Web. (Advanced Information and Knowledge

Processing). Springer-Verlag, New York.

G. S. Davidson, e. a. (2010). Data Mining for Ontology

Development. Sandia National Laboratories, Albu-

querque.

Gorskis, H. and Chizhof, Y. (2012). Ontology building us-

ing data mining techniques. Information Technology

and Management Science, 15:183–188.

N. F. Noy, D. L. M. (2001). Ontology Development 101:

A Guide to Creating Your First Ontology. Stanford

University, Stanford.

DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications

376