
Using Bitmaps for Executing Range Queries in Encrypted Databases
Lil Mar´ıa Rodr´ıguez-Henr´ıquez and Debrup Chakraborty
Departamento de Computaci´on, CINVESTAV-IPN
Av. Instituto Polit´ecnico Nacional No. 2508, Col. San Pedro Zacatenco, Mexico D.F. 07300, Mexico
Keywords:
Symmetric Encryption, Database Encryption, Deterministic Encryption, Bitmap Index, Provable Security.
Abstract:
Privacy of data stored at un-trusted servers is an important problem of today. A solution to this problem can be
achieved by encrypting the outsourced data, but simple encryption does not allow efficient query processing.
In this paper we propose a novel scheme for encrypting relational databases so that range queries can be
efficiently executed on the encrypted data. We formally define the syntax and security of the problem and
specify a scheme called ESRQ1. ESRQ1 uses a deterministic encryption scheme along with bitmap indices to
encrypt a relational database. We provide details of the functionality of ESRQ1 and prove its security in the
specified model.
1 INTRODUCTION
Encryption, if applied to relational databases, should
be done in such a way that a large class of queries
can be executed on the encrypted tables. For exam-
ple, if we consider the relation R1 shown in Table 1
some representative queries on this relation can be:
(1) What are the names of the employees whose age
is 18 years? (2) What are the names of the employ-
ees whose age is more than 30 years? (3) What is the
average age of an employee?
If the relation R1 is encrypted normally, i.e., en-
crypting separately each cell of the relation with a
strong (say a IND-CPA secure) encryption, then none
of the above queries can be executed on the encrypted
table.
Regarding the queries that we posed above, query
(1) can be addressed if the relation is encrypted us-
ing a deterministic encryption scheme, such encryp-
tion preserves the equality relation of plaintexts. For
query (2), it is required that the ciphertexts maintains
the order of the plaintexts, this can be achieved by
order preserving encryption. Finally, for query (3) it
is required that meaningful computations can be per-
formed on the ciphertexts, homomorphic encryption
schemes can support such computations on encrypted
data. Generally to treat a large class of queries dif-
ferent encryption mechanisms on the same database
is used. Among others, this paradigm is followed in a
recent work (Popa et al., 2011). In this work we will
mainly focus on processing a class of range queries
(query (2) in the example above).
To enable range queries in an encrypted database
the ciphertext values should provide order informa-
tion of the plaintexts. This can be achieved by an or-
der preserving encryption (OPE) scheme. An OPE
scheme E is such a scheme where E(x) ≥ E(y), iff
x ≥ y. This interesting primitive has received lot of
attention in the current years. The first concepts ap-
peared in the paper (Agrawal et al., 2004), where
the main aim was to design a scheme where effi-
cient range queries can be executedon encrypted data.
This work does not delve into formal definitional and
security perspectives of OPE. The first work which
formally deals with OPE is (Boldyreva et al., 2009),
where the ideal security notion for an OPE scheme,
IND-OCPA, was introduced. The IND-OCPA defini-
tion specifies that the main goal for an OPE is to re-
veal no additional information about the plaintext val-
ues besides their order. In (Boldyreva et al., 2009) it
was shown that it is infeasible to achieve IND-OCPA
security with a stateless encryption scheme. As a re-
sult, they settled on a weaker security guarantee that
was later shown in (Boldyreva et al., 2011) to leak
at least half of the plaintext bits. Later, several other
order preserving schemes were proposed (Boldyreva
et al., 2011; Lee et al., 2009; Yum et al., 2012), but as
it is suggested in (Popa et al., 2013) none of them has
achieved the ideal IND-OCPA security.
Recently, in (Popa et al., 2013), the first ideal-
security order-preserving encoding scheme was pro-
posed, where the ciphertexts revealnothing except the
order of the plaintext values. The insight that allow
them to avoid the infeasibility result in (Boldyreva
432
María Rodríguez-Henríquez L. and Chakraborty D..
Using Bitmaps for Executing Range Queries in Encrypted Databases.
DOI: 10.5220/0005111604320438
In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 432-438
ISBN: 978-989-758-045-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: The relation R1.
EmpId Name Age
TRW Tom 18
MST Mary 17
JOH John 52
MRH Mary 33
ASY Anne 18
RZT Rosy 36
et al., 2009) is that the encryption protocol proposed
is interactive, and a small number of ciphertexts of
already-encrypted values change, as new plaintext
values are encrypted. A property which the authors
terms as “mutable”.
Our Contributions. We see the problem of execut-
ing range queries in an encrypted database from a
different direction. The main component of our so-
lution is not to use any special type of encryption
scheme, i.e., the encryption scheme we use is not an
OPE scheme. We encrypt the tables with a determin-
istic encryption scheme, additionally we maintain an-
other table which contains just the order information
of the various attribute values. Both of these tables
are kept with the server, and the server can respond
to range queries without the knowledge of the real
attribute values in the table. We propose a generic
framework for a database encryption scheme support-
ing range queries (ESRQ), and define its syntax and
security notion. We also provide a complete scheme
called ESRQ1. A novel component of ESRQ1 is that
it uses bitmap indices to encode the order information
of the attributes. Bitmap indices are gaining popular-
ity in the current days for accelerated query process-
ing, and many commercial databases now implement
them. Thus it is likely that our solution can be adopted
in an existing database easily and efficiently. To our
knowledge bitmaps have not been used previously to
ensure privacy of databases.
2 PRELIMINARIES
Relations. In what follows, by R(A) we would
denote a relation over a set of attributes A.
If A = {a
1
,a
2
,···a
m
}, we shall sometimes write
R(a
1
,a
2
,··· ,a
m
). Given an attribute a, Dom
R
(a)
would represent the distinct values of the attribute a
in the relation R.
By cardinality of an attribute a in R we shall
mean the cardinality of Dom
R
(a), i.e. Card
R
(a) =
|Dom
R
(a)|.
A tuple t in a relation over a set of attributes is a
function that associates with each attribute a value in
its specific domain. Specifically if A = {a
1
,a
2
,···a
m
}
and R(A) be a relation, then the j
th
tuple of R(A)
would be denoted by t
R
j
. And for a
i
∈ A, by t
R
j
[a
i
]
we shall denote the value of attribute a
i
in the j
th
tu-
ple in R. For B ⊆ A, t
R
j
[B] will denote the set of values
of the attributes in B in the j
th
tuple. We shall some-
times omit the subscripts and superscripts from t
R
j
and
denote the tuple by t if the concerned relation is clear
from the context and the tuple number is irrelevant.
Binary Strings. The set of all binary strings would
be denoted by {0, 1}
∗
, and the set of n bit strings
by {0,1}
n
. For X
1
,X
2
∈ {0, 1}
∗
, by X
1
||X
2
we shall
mean the concatenation of X
1
and X
2
; |X
1
| will denote
the length of X
1
in bits; and
X
1
will denote the bit-
wise complement of X
1
. If |X
1
| = |X
2
|, and ⊚ be a
Boolean operator then by X
1
⊚X
2
we will mean that
the operation ⊚ is applied bitwise. For X ∈ {0,1}
n
and 1 ≤ k ≤ n, bit
k
(X) will denote the k
th
bit of X.
We shall always consider that the domains of all
attributes in the relations and attribute names are sub-
sets of {0,1}
∗
, this convention would allow us to ap-
ply transformations and functions on the values of the
tuples in a relation without describing explicit encod-
ing schemes.
Bitmaps. Consider a relation R(a
1
,...,a
m
) with
nT many rows. Consider that for each attribute a
i
,
Dom
R
(a
i
) = {v
i
1
,v
i
2
,...v
i
λ
i
}, thus Card
R
(a
i
) = λ
i
for
1 ≤ i ≤ m. We define the bitmap of an attribute
a
i
corresponding to its value v
i
j
in the relation R as
BitMap
R
(a
i
,v
i
j
) = X, where X is a binary string, such
that |X| = nT and for 1 ≤ k ≤ nT,
bit
k
(X) =
1 if t
R
k
[a
i
] = v
i
j
0 otherwise.
The encoding for the previous definition is known
as equality encoding, we shall call such bitmaps as
e-encoded bitmaps. In the literature there are other
kinds of bitmap encodings to allow different kinds of
queries. We would be interested in two types of range
bitmaps BitMap
<
and BitMap
>
which we will fur-
ther call as l-encoded and g-encoded bitmaps respec-
tively. For the relation R described above, we have
BitMap
<
R
(a
i
,v
i
j
) = Y, where
bit
k
(Y) =
1 if t
R
k
[a
i
] < v
i
j
0 otherwise.
From the l-encoding and e-encoding other bitmap en-
codings can be easily derived. For example, we define
BitMap
>
R
(a
i
,v
i
j
) =
BitMap
<
R
(a
i
,v
i
j
) ⊕ BitMap
R
(a
i
,v
i
j
)
BitMap
≤
R
(a
i
,v
i
j
) = BitMap
<
R
(a
i
,v
i
j
) ∨ BitMap
R
(a
i
,v
i
j
)
BitMap
≥
R
(a
i
,v
i
j
) =
BitMap
<
R
(a
i
,v
i
j
)
UsingBitmapsforExecutingRangeQueriesinEncryptedDatabases
433

In what follows we will sometimes use two proce-
dures related to bitmaps. Let nT be a positive integer
and S ⊆ {1,2...,nT}. MakeBitMap(nT,S) outputs
a string X such that |X| = nT and for 1 ≤ k ≤ nT,
bit
k
(X) = 1 if k ∈ S and bit
k
(X) = 0, otherwise. If
Y ∈ {0,1}
nT
, then MakeSet(Y) returns the set S =
{i : 1 ≤ i ≤ nT and bit
i
(Y) = 1}.
Deterministic Encryption Schemes: A determinis-
tic encryption scheme with associated data (DEAD) is
a deterministic function E : K × T × M → C , where
K , T , M and C are the key space, tweak (associated
data) space, message space and cipher space, respec-
tively. Thus, E receives as input a key K ∈ K , a tweak
T ∈ T and a message M ∈ M and produces as output
a cipher C ∈ C . We shall often write E
K
(T,M) in-
stead of E(K,T, M). E also has an inverse function
D : K × T × C → M , such that for every K ∈ K , ev-
ery T ∈ T and every M ∈ M , D
K
(T,E
K
(T,M)) = M.
This implies that for every T ∈ T and every K ∈ K ,
E
K
(T,·) : M → C is an injective function.
To define security of E we consider an adversary
A which is given an oracle O. The oracle O can either
be E
K
(·,·), i.e., the encryption scheme which is in-
stantiated with a uniform random key K selected from
K , or it can be $(·,·) which is an oracle which on in-
put (T,M) ∈ T × M outputs a random string of size
|E
K
(T,M)|. One important restriction of A is that it is
not allowed to repeat any query. We formally define
the advantage of A as
Adv
det-cpa
E
(A) = | Pr[K
$
← K : A
E
K
(·,·)
⇒ 1] −
Pr[A
$(·,·)
⇒ 1]|
We define Adv
det-cpa
E
(q,σ
n
,t) by
max
A
Adv
det-cpa
E
(A) where maximum is taken
over all adversaries which makes at most q queries
having at most σ
n
many blocks (of n bits) and runs for
time at most t. We consider an encryption scheme to
be (ε,q,t) det-cpa secure if Adv
det-cpa
E
(q,σ
n
,t) ≤ ε.
3 ESRQ: BASIC NOTIONS
An encryption scheme supporting range queries
(ESRQ) consists of a tuple of algorithms
(K ,Enc, Φ,Ψ,Dec), which work as follows.
The key Generation Algorithm K runs at the
client side and outputs a set of keys that are ran-
domly selected from a pre-specified key space.
We will sometimes denote the key space also by
K .
Game ESRQ
A
ϒ
1. The challenger selects K
$
← K
2. A selects two relations R
0
, R
1
, such that
R
0
≈ R
1
, and gives them to the challenger.
3. The challenger selects a bit b
$
← {0,1}
4. The challenger computes R
′
← ϒ.Enc
K
(R
b
),
and gives it to A.
5. A outputs a bit b
′
.
6. if b = b
′
output 1
7. else output 0
Figure 1: Game used to define security of ESRQ.
The Privacy Transform Enc receives as an input
a relation called R and the set of keys generated
by K . This transform generates a new set of en-
crypted relations called R
′
. We denote this opera-
tion as R
′
← Enc
K
(R). This transform is executed
in the client side.
The Query Translator Φ is a keyed transform
that runs at the client. It takes in the key K and
a query q meant for the relation R and converts it
to a query q
′
which can be executed in R
′
. For
convenience, we shall sometimes refer to a query
meant for R to be a R-query and a query meant for
R
′
as R
′
-query.
The Response Procedure Ψ runs at the server
side. Ψ allows the server to answer a query Φ(q)
on R
′
. The output of Ψ for a query is the response
of the server, called ρ. ρ contains the encrypted
answer, the server returns it to the client.
The Decryption Procedure is a keyed transform
Dec
K
which runs in the client. It receives as input
the server response ρ and outputs the answer ans
for the query q.
3.1 Security Notion
Definition 1. Given a relation R over a set of at-
tributes A, we classify the attributes in two different
classes: the ones where a range query is valid (range
attributes) and the ones where such queries are not
valid. Define ty : A → {0, 1}, where for any a ∈ A,
ty(a) = 0, if range queries on the attribute a is not
applicable and ty(a) = 1, otherwise.
Definition 2. Two relations R and S are said to be
equivalent (denoted by R ≈ S) if the following condi-
tions hold.
1. R and S are defined over the same set of attributes A.
2. R and S contains the same number of tuples nT.
3. For every i, j ∈ {1, 2,... ,nT}, and every a ∈ A, t
R
i
[a] =
t
R
j
[a] ⇐⇒ t
S
i
[a] = t
S
j
[a].
SECRYPT2014-InternationalConferenceonSecurityandCryptography
434

4. For every i, j ∈ {1,2,. . . ,nT}, and every a ∈ A, such
that ty(a) = 1,
t
R
i
[a] ≥ t
R
j
[a] ⇐⇒ t
S
i
[a] ≥ t
S
j
[a].
5. For every i ∈ {1,2,.. . , nT}, and every a ∈ A, |t
R
i
[a]| =
|t
S
i
[a]|.
The basic goal of ESRQ is to transform R to R
′
in
such a way that R
′
should not contain any information
beyond the order relation between the attribute values.
We formally define security of an ESRQ ϒ as a game
between an adversary and a challenger, see Figure 1.
Definition 3. The advantage of an adversary A in
attacking an ESRQ ϒ is defined as
Adv
esrq
ϒ
(A) =
Pr[ESRQ
A
⇒ 1] −
1
2
.
The relevant resources of an adversary attacking
an ESRQ scheme is its running time and the size
of the relations that it chooses and submits to its
challenger. We measure the size of the relation in
two different ways, we denote by q the number of
cells. Let s
i
be the size of each cell, then we define
σ
n
=
∑
q
i=1
⌈s
i
/n⌉. We call q as the cell complexity of
A and σ
n
as the query complexity of A. We define
Adv
esrq
ϒ
(q,σ
n
,t) = maxAdv
esrq
ϒ
(A), where the max-
imum is taken over all adversaries A which runs for
time at most t and has cell complexity and query com-
plexity of at most q and σ
n
, respectively. Moreover,
we say that an ESRQ scheme ϒ is (ε,q,σ
n
,t) secure,
if Adv
esrq
ϒ
(q,σ
n
,t) ≤ ε.
3.2 ESRQ1
Here we discuss a specific scheme ESRQ1 for en-
crypting relations such that simple select and range
queries can be executed in the encrypted relations.
Consider a relation R(A) where A = {a
1
,a
2
,...a
|A|
},
and the function ty : A → {0,1} defined on A. We
consider that a client wants to outsource this generic
relation R(A) to a server. To ensure privacy, the client,
encryptsthe relation R(A) using ESRQ1 and delegates
this encrypted relation instead of the original one.
The client will pose queries to the server and expects
that the server to execute these queries on his/her be-
half without knowing the real contents of the relation
R(A).
In what follows, we present a generic description
of the scheme, also throughout we discuss a specific
example based on the relation shown in Table 1. The
only cryptographic object used by ESRQ1 is a deter-
ministic encryption scheme E which is required to be
det-cpa secure. We assume that E : K × {0,1}
λ
×
{0,1}
∗
→ {0,1}
∗
. Other than the deterministic en-
cryption scheme E, ESRQ1 uses bitmap indices.
The various algorithms involved in ESRQ1 are
discussed next in order.
ESRQ1.K : This procedure selects a key K uniformly
at random from K . Where K is the key space of the
deterministic encryption scheme E involved.
ESRQ1.Enc: Given R(A) and the key K as input,
ESRQ1.Enc outputs two relations R
α
and R
β
. We
assume that R(A) contains nT many tuples and A =
{a
1
,a
2
,...,a
|A|
}. To each attribute a
i
∈ A we asso-
ciate an unique identifier id
i
∈ {0, 1}
λ
. Among other
possibilities, this identifier can be the (appropriately
encoded) name of the attribute or a counter.
R
α
contains nT tuples and is defined over the at-
tributes B = {Row} ∪ {b
1
,b
2
,...,b
|A|
}. Where b
i
=
E
K
(id
∗
,a
i
) for some id
∗
∈ {0,1}
λ
such that id
∗
/∈
{id
1
,id
2
,...,id
|A|
}. Hence, R
α
has one attribute more
than in R, the extra attribute is RowNo, the other at-
tributes of R
α
are the encryptionof the attribute names
in A. The specific way in which R
α
is created from R
is shown in Figure 2, which shows that R
α
contains
the encryption of the values present in R.
The relation R
β
contains the attributes
{Name,SearchKey,BitMap}, irrespective of the
attributes in relation R. The way the relation R
β
is
populated is shown in Figure 2. R
β
stores information
regarding each range attribute in A. For a range
attribute a
i
all its values occurring in R are encrypted.
These encrypted values along with the corresponding
attribute name and the l-encoded bitmap are stored in
R
β
.
For a concrete example, consider that ESRQ1.Enc
has as input the relation R1 as shown in Table 1. The
only attribute in R1, where range queries are mean-
ingful is the attribute
Age
. Then ESRQ1.Enc(R1)
would produce as output the relations R1
α
and R1
β
as shown in Table 2. While applying encryption, the
unique identifier of each column is used as the associ-
ated data. The attribute names of the original relation
R1 occur in R1
α
in the encrypted form.
The relation R1
β
is created as described in Figure
2. The basic idea is to store the order information
of all the values corresponding to the range attributes
in a suitable manner. The table stores the encrypted
values along with the encrypted attribute names. The
order information is stored in the form of l-encoded
bitmaps. Note that, for encrypting a specific value the
identifier of the attribute is used as the associated data.
ESRQ1.Φ: The transform Φ receives as input a query
meant for R and converts it to a query which can be
executed in (R
α
,R
β
). The allowed set of queries are
simple select queries and range queries. The generic
format of an allowed query is
Q:
SELECT * FROM
R
WHERE
(a
1
⊳
1
v
1
) ⊚
1
(a
1
⊳
2
v
2
) ⊚
2
......
⊚
ℓ−1
(a
ℓ
⊳
1
v
ℓ
)
,
UsingBitmapsforExecutingRangeQueriesinEncryptedDatabases
435
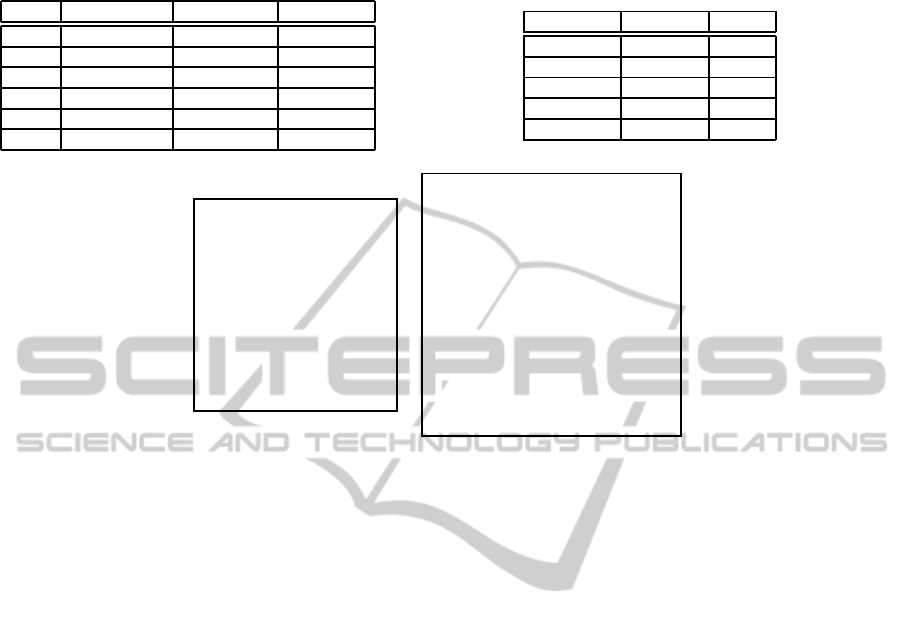
Table 2: Relations R1
α
and R1
β
.
Relation R1
α
RowNo
E
K
(id
∗
,EmpId) E
K
(id
∗
,Name) E
K
(id
∗
,Age)
1 E
K
(id
1
,TRW) E
K
(id
2
,Tom) E
K
(id
3
,18)
2 E
K
(id
1
,MST) E
K
(id
2
,Mary) E
K
(id
3
,17)
3 E
K
(id
1
,JOH) E
K
(id
2
,John) E
K
(id
3
,52)
4 E
K
(id
1
,MRH) E
K
(id
2
,Mary) E
K
(id
3
,33)
5 E
K
(id
1
,ASY) E
K
(id
2
,Anne) E
K
(id
3
,18)
6 E
K
(id
1
,RZT) E
K
(id
2
,Rosy) E
K
(id
3
,36)
Relation R1
β
Name SearchKey BitMap
E
K
(id
∗
,Age) E
K
(id
3
,17) 000000
E
K
(id
∗
,Age) E
K
(id
3
,18) 010000
E
K
(id
∗
,Age) E
K
(id
3
,33) 110010
E
K
(id
∗
,Age) E
K
(id
3
,36) 110110
E
K
(id
∗
,Age) E
K
(id
3
,52) 110111
Creating R
α
1. for j = 1 to |A|,
2. b
j
← E
K
(id
∗
,a
j
);
3. end for
4. for j = 1 to nT,
5. t
R
α
j
[RowNo] ← j;
6. for i = 1 to |A|,
7. t
R
α
j
[b
i
] ← E
K
(id
i
,t
R
j
[a
i
]);
8. end for
9. end for
Creating R
β
1. j → 1
2. for i = 1 to |A|
3. if ty(a
i
) = 1,
4. for all v ∈ Dom(a
i
),
5. t
R
β
j
[Name] ← E
K
(id
∗
,a);
6. t
R
β
j
[SearchKey] ← E
K
(id
i
,v);
7. t
R
β
j
[BitMap] ← BitMap
<
R
(a
i
,v);
8. j ← j+ 1
9. end for
10. end if
11.end for
Figure 2: Creating R
α
and R
β
.
where a
i
represent an attribute name and v
i
a value
of the attribute. ⊳
i
∈ {>, <,≤,≥}, and ⊚
i
can be an
arbitrary Boolean connective, say ∨, ∧ etc.
Given as input a valid query Q, Φ(Q) is the trans-
lation of the original query which just hides the at-
tribute names and the values assigned to the attributes
by encryption. As the input query has a specific struc-
ture, hence the translated query Φ(Q) is just
Q
′
: (c
1
⊳
1
c
′
1
)⊚
1
(c
2
⊳
2
c
′
2
)⊚
2
......⊚
ℓ−1
(c
ℓ
⊳
1
c
′
ℓ
),
where c
i
= E
K
(id
∗
,a
i
) and c
′
i
= E
K
(id
i
,v
i
).
Going back to the concrete example, consider the
following query Q1 for the relation R1
Q1:
SELECT * FROM
R
WHERE Age
≥ 18
AND Age
≤ 36
The transformation Φ(Q1), will output
Q1
′
: (E
k
(id
∗
,Age) ≥ E
K
(id
3
,18))
V
(E
k
(id
∗
,Age) ≤
E
K
(id
3
,36))
This transformed query is sent to the server.
ESRQ1.Ψ: As discussed, Ψ is the transform that runs
in the server to execute the client’s instructions. The
instruction from the client comes to the server en-
coded as Q
′
, and it executes the procedure Ψ(Q
′
) as
described in Figure 3. Ψ treats the equality/inequality
conditions in Q
′
separately, and constructs a bitmap
for each of these conditions. Once the bitmaps for the
individual conditions are constructed, it aggregates
the bitmaps using the given Boolean connectives. The
final bitmap B constructed in line 13 contains the in-
formation regarding the tuples in R
α
, which satisfies
the client’s query.
Going back to our example, the query Q1
′
consists of two inequality conditions. The first
one is (E
K
(id
∗
,Age) ≥ E
K
(id
3
,18)), the bitmap
for this condition is constructed by checking the
relation R
β
, the bitmap corresponding to Name =
E
K
(id
∗
,Age) AND SearchKey = E
K
(id
3
,18) is
010000. But recall that the bitmap stored in
R
β
is the l-encoded bitmap. Hence, the bitmap
for the condition (E
K
(id
∗
,Age) ≥ E
K
(id
3
,18))
would be the complement of the stored bitmap,
i.e., 101111. The bitmap for the second con-
dition (E
k
(id
∗
,Age) ≤ E
K
(id
3
,36)) is computed
by retrieving the l-encoded bitmap for Name =
E
K
(id
∗
,Age) AND SearchKey = E
K
(id
3
,36) that
is equal to 110110. Then the e-encoded bitmap is
computed from R
α
, i.e., 000001. Finally these two
bitmaps are operated by an OR bitwise, giving as
result 110111. As in the query the two conditions
are connected by an
AND
, hence the bitmap for the
query is 101111 ∧ 110111 = 100111. This bitmap
corresponds to the rows 1, 4, 5 and 6 of the table R
α
.
Hence the server sends the tuples in R
α
corresponding
to these row numbers.
ESRQ1.Dec: The decryption procedure receives as
input the response S from the server and the keys.
This procedure uses the inverse of the encryption E
−1
K
to decrypt the server response.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
436
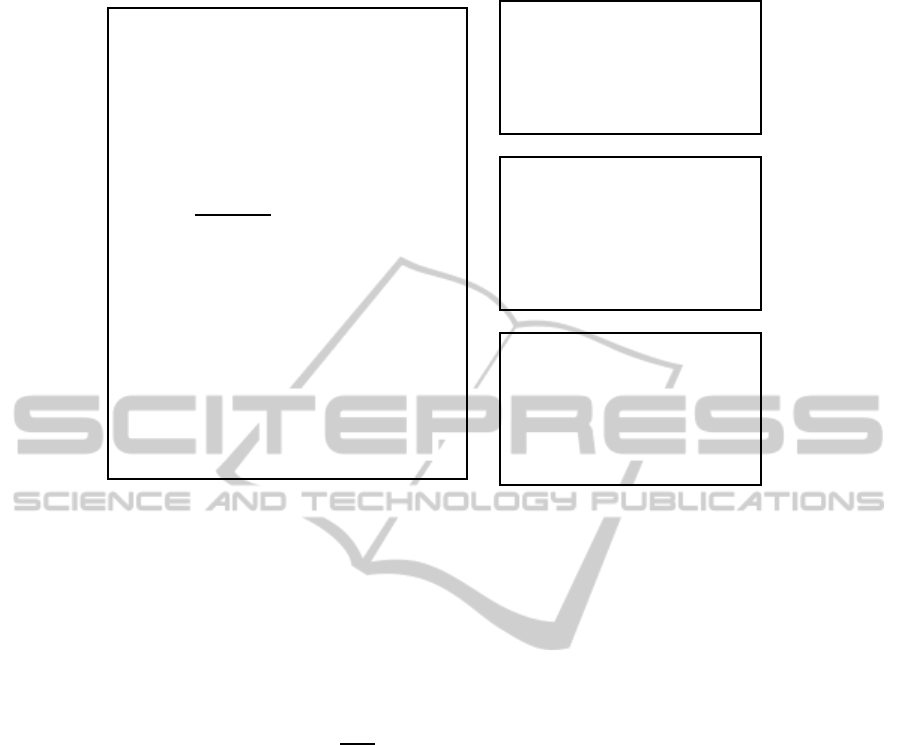
Response Procedure Ψ(Q
′
)
(Assume Q
′
≡ (c
1
⊳
1
c
′
1
)⊚
1
(c
2
⊳
2
c
′
2
)⊚
2
......⊚
ℓ−1
(c
ℓ
⊳
1
c
′
ℓ
))
1. for i ← 1 to ℓ
2. if ⊳
i
is ’=’,
3. B
i
← Equal(c
i
,c
′
i
)
4. if ⊳
i
is ’<’,
5. B
i
← Lesser(c
i
,c
′
i
)
6. if ⊳
i
is ’>’,
7. B
i
← Greater(c
i
,c
′
i
)
8. if ⊳
i
is ’≥’,
9. B
i
←
Lesser(c
i
,c
′
i
)
10. if ⊳
i
is ’≤’,
11. B
i
← Lesser(c
i
,c
′
i
) ∨ Equal(c
i
,c
′
i
)
12.end for
13.B ← B
1
⊚
1
B
2
⊚
2
··· ⊚
ℓ−1
B
ℓ
14.Σ ← MakeSet(B, nT)
( Let Σ = {σ
1
,σ
2
,... ,σ
m
})
15.Run the query:
SELECT * FROM
R
α
WHERE
RowNo IN (
σ
1
,σ
2
,... ,σ
m
)
16.Let S be the response to the above query;
17.return S;
Equal(a,b)
1. Run the query:
SELECT RowNo from
R
α
where a =b
2. Let S be the response of the above query
3. B ← MakeBitMap(nt,S)
4. return B
Lesser(a, b)
1. Run the query:
SELECT BitMap FROM
R
β
where
Name = a AND SearchKey = b
2. Let S be the response of the above query
and B ∈ S,
3. return B
Greater(a,b)
1. Run the query:
SELECT BitMap FROM
R
β
where
Name = a AND SearchKey = b
2. Let S be the response of the above query
and B ∈ S,
3. return
¯
B⊕ Equal(a, b)
Figure 3: The response procedure Ψ.
Security of ESRQ1: Let ESRQ1[E] denote a ESRQ
scheme where the deterministic encryption used is E.
Theorem 1. Fix natural numbers q,σ
n
,t, and a de-
terministic encryption scheme E : K × T × M → C ,
such that the smallest ciphertext in C has size s. Let
ϒ = ESRQ1[E]. Then
Adv
esrq
ϒ
(q,σ
n
,t) ≤ Adv
det-cpa
E
(q
′
,σ
′
n
,t
′
) +
q
2
2
s+1
,
where q
′
≤ q, σ
′
n
≤ σ
n
and t
′
= O(t).
The above Theorem relates the esrq security of
ESRQ1[E], with the det-cpa security of E, and it
implies that the ESRQ1 scheme provides almost the
same security as that of E with a small degradation.
4 CONCLUSION
In this paper we described a generic framework for
database encryptions which enables range queries.
We also specified a novel scheme called ESRQ1
which uses deterministic encryption and bitmap in-
dices. This initial proposal is being extended in sev-
eral ways: management for dynamic databases, a new
scheme which would provide just det-cpa security,
and an efficient implementation of this scheme on a
postgres SQL database. These results would be soon
appear in an extended version of this paper.
ACKNOWLEDGEMENTS
The authors acknowledge the support from CONA-
CyT project 166763.
REFERENCES
Agrawal, R., Kiernan, J., Srikant, R., and Xu, Y. (2004).
Order-preserving encryption for numeric data. In
Weikum, G., K¨onig, A. C., and Deßloch, S., editors,
SIGMOD Conference, pages 563–574. ACM.
Boldyreva, A., Chenette, N., Lee, Y., and O’Neill, A.
(2009). Order-preserving symmetric encryption. In
Joux, A., editor, EUROCRYPT, volume 5479 of Lec-
ture Notes in Computer Science, pages 224–241.
Springer.
Boldyreva, A., Chenette, N., and O’Neill, A. (2011). Order-
preserving encryption revisited: Improved security
analysis and alternative solutions. In Rogaway, P., ed-
itor, CRYPTO, volume 6841 of Lecture Notes in Com-
puter Science, pages 578–595. Springer.
Lee, S., Park, T.-J., Lee, D., Nam, T., and Kim, S. (2009).
Chaotic order preserving encryption for efficient and
secure queries on databases. IEICE Transactions, 92-
D(11):2207–2217.
Popa, R. A., Li, F. H., and Zeldovich, N. (2013). An ideal-
security protocol for order-preserving encoding. In
IEEE Symposium on Security and Privacy, pages 463–
477. IEEE Computer Society.
Popa, R. A., Redfield, C. M. S., Zeldovich, N., and Balakr-
ishnan, H. (2011). Cryptdb: protecting confidentiality
UsingBitmapsforExecutingRangeQueriesinEncryptedDatabases
437

with encrypted query processing. In SOSP, pages 85–
100.
Yum, D., Kim, D., Kim, J., Lee, P., and Hong, S. (2012).
Order-preserving encryption for non-uniformly dis-
tributed plaintexts. In Jung, S. and Yung, M., edi-
tors, Information Security Applications, volume 7115
of Lecture Notes in Computer Science, pages 84–97.
Springer Berlin Heidelberg.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
438
